Python ::: Desafios e Lista de Exercícios Resolvidos ::: Engenharia Civil - Cálculo Estrutural

Exercícios Resolvidos de Python - Como calcular as reações de apoio, momento de flexão máxima e forças cortantes em uma viga bi-apoiada com carga distribuída retangular usando Python

Quantidade de visualizações: 1782 vezes

Pergunta/Tarefa:

Veja a seguinte figura: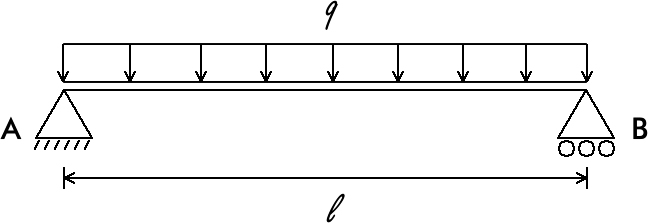

Nesta imagem temos uma viga bi apoiada com uma carga q distribuída de forma retangular a uma distância l. Para fins didáticos, vamos considerar que a carga q será em kN/m e a distância l será em metros. O apoio A é de segundo gênero e o apoio B é de primeiro gênero.

Escreva um programa Python que solicita ao usuário que informe o valor da carga q e a distância l entre os apoios A e B. Em seguida mostre os valores das reações nos apoios A e B, o momento de flexão máxima da viga e o momento de flexão para uma determinada distância (que o usuário informará) a partir do apoio A.

Mostre também as forças cortantes nos apoios A e B. Lembre-se de que, para uma carga distribuída de forma retangular, o diagrama de momento fletor é uma parábola, enquanto o diagrama de cortante é uma reta (com o valor zero para a força cortante no meio da viga).

Sua saída deve ser parecida com:

Valor da carga em kN/m: 10
Distância em metros: 13

A reação no apoio A é: 65.000000 kN
A reação no apoio B é: 65.000000 kN
O momento fletor máximo é: 211.250000 kN.m

Informe uma distância a partir do apoio A: 4
O momento fletor na distância informada é: 180.000000 kN.m

A força cortante no apoio A é: 65.000000 kN
A força cortante no apoio B é: -65.000000 kN

Resposta/Solução:

Veja a resolução comentada deste exercício usando Python:

----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------

# Algoritmo que calcula reação de apoio, momento fletor
# e força cortante em uma viga bi-apoiada em Python

# vamos importar o módulo Math
import math

# função principal do programa
def main():
  # vamos pedir para o usuário informar o valor da carga
  carga = float(input("Valor da carga em kN/m: "))
  
  # vamos pedir para o usuário informar a distância entre os apoios
  distancia = float(input("Distancia em metros: "))
  
  # vamos calcular a reação no apoio A
  reacao_a = (1.0 / 2.0) * carga * distancia
  
  # vamos calcular a reação no apoio B
  reacao_b = reacao_a
  
  # vamos calcular o momento fletor máximo
  flexao_maxima = (1.0 / 8.0) * carga * math.pow(distancia, 2.0)
  
  # e mostramos o resultado
  print("\nA reação no apoio A é: {0} kN".format(reacao_a))
  print("A reação no apoio B é: {0} kN".format(reacao_b))
  print("O momento fletor máximo é: {0} kN.m".format(flexao_maxima))
  
  # vamos pedir para o usuário informar uma distância a
  # partir do apoio A
  distancia_temp = float(input("\nInforme uma distância a partir do apoio A: "))
  # vamos mostrar o momento fletor na distância informada
  if distancia_temp > distancia:
    print("\nDistância inválida.")
  else:
    flexao_distancia = (1.0 / 2.0) * carga * distancia_temp * \
      (distancia - distancia_temp)
    print("O momento fletor na distância informada é: {0} kN.m".format(
      flexao_distancia))  
   
  # vamos mostrar a força cortante no apoio A
  cortante_a = (1.0 / 2.0) * carga * distancia
  print("\nA força cortante no apoio A é: {0} kN".format(cortante_a))
  
  # vamos mostrar a força cortante no apoio B
  cortante_b = cortante_a * -1
  print("A força cortante no apoio B é: {0} kN".format(cortante_b))
  
if __name__== "__main__":
  main()

GNU Octave ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas

Como calcular o coeficiente angular de uma reta em GNU Octave dados dois pontos no plano cartesiano

Quantidade de visualizações: 1625 vezes

O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x.

Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:

Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é:

\[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \]

Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente.

Veja agora o trecho de código na linguagem GNU Octave (script GNU Octave) que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:

----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------

# x e y do primeiro ponto
x1 = input("Coordenada x do primeiro ponto: ")
y1 = input("Coordenada y do primeiro ponto: ")

# x e y do segundo ponto
x2 = input("Coordenada x do segundo ponto: ")
y2 = input("Coordenada y do segundo ponto: ")

# agora vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1)

# mostramos o resultado
fprintf("O coeficiente angular é: %f\n\n", m)

Ao executar este código em linguagem GNU Octave nós teremos o seguinte resultado:

Coordenada x do primeiro ponto: 3
x1 = 3
Coordenada y do primeiro ponto: 6
y1 = 6
Coordenada x do segundo ponto: 9
x2 = 9
Coordenada y do segundo ponto: 10
y2 = 10
m = 0.6667
O coeficiente angular é: 0.666667

Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):

----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------

# x e y do primeiro ponto
x1 = input("Coordenada x do primeiro ponto: ")
y1 = input("Coordenada y do primeiro ponto: ")

# x e y do segundo ponto
x2 = input("Coordenada x do segundo ponto: ")
y2 = input("Coordenada y do segundo ponto: ")

# vamos obter o comprimento do cateto oposto
cateto_oposto = y2 - y1
# e agora o cateto adjascente
cateto_adjascente = x2 - x1
# vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
# (em radianos, não se esqueça)
tetha = atan2(cateto_oposto, cateto_adjascente)
# e finalmente usamos a tangente desse ângulo para calcular
# o coeficiente angular
tangente = tan(tetha)

# mostramos o resultado
fprintf("O coeficiente angular é: %f\n\n", tangente)

Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta:

1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0;

2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0;

3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0).

4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe.

Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes)

Exercício Resolvido de Java - Desenvolva um programa que leia dez números do tipo inteiro ao usuário Armazene esses dez números em um vetor

Quantidade de visualizações: 1470 vezes

Exercício Resolvido de Java - Desenvolva um programa que leia dez números do tipo inteiro ao usuário. Armazene esses dez números em um vetor

Pergunta/Tarefa:

Desenvolva um programa que leia dez números do tipo inteiro ao usuário. Armazene esses dez números em um vetor. Para os valores dos elementos inseridos nas posições pares desse vetor, calcule o somatório deles, para os demais calcule a subtração desses valores. Em seguida, o programa deverá apresentar na tela os resultados.

Sua saída deverá ser parecida com:

Digite o 1.o número inteiro: 5
Digite o 2.o número inteiro: 1
Digite o 3.o número inteiro: 2
Digite o 4.o número inteiro: 3
Digite o 5.o número inteiro: 7
Digite o 6.o número inteiro: 8
Digite o 7.o número inteiro: 10
Digite o 8.o número inteiro: 54
Digite o 9.o número inteiro: 4
Digite o 10.o número inteiro: 5
A soma dos números nas posições pares é: 28
A subtração dos números nas posições ímpares é: -71

Resposta/Solução:

Veja a resolução comentada deste exercício usando Java:

----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------

package estudos;

import java.util.Scanner;

public class Estudos {
  public static void main(String[] args) {
    // para ler a entrada do usuário
    Scanner entrada = new Scanner(System.in);

    int numeros[] = new int[10]; // vetor para guardar os 10 números inteiros
    int soma = 0; // soma dos números nas posições pares
    int subtracao = 0; // subtração dos números nas posições impares
    
    // vamos fazer a leitura dos 10 valores inteiros
    for(int i = 0; i < numeros.length; i++){
      System.out.print("Digite o " + (i + 1) + ".o número inteiro: ");
      numeros[i] = Integer.parseInt(entrada.nextLine());
    }
    
    // agora vamos percorrer o vetor e obter a soma dos elementos nas posições
    // pares e a subtração dos elementos nas posições ímpares
    for(int i = 0; i < numeros.length; i++){
      if(i % 2 == 0){
        // posição par
        soma = soma + numeros[i];
      }
      else{
        // posição ímpar
        subtracao = subtracao - numeros[i];
      }
    }
    
    System.out.println("A soma dos números nas posições pares é: " + soma);
    System.out.println("A subtração dos números nas posições ímpares é: " 
      + subtracao);
  }
}

PHP ::: Fundamentos da Linguagem ::: Tipos de Dados

Como usar o tipo de dados object da linguagem PHP

Quantidade de visualizações: 7950 vezes

O PHP, especialmente a partir da versão 5.0, suporta a programação orientada a objetos (OOP). A programação OOP promove um design modular limpo, simplifica a depuração e manutenção e facilita a reutilização de códigos.

As classes são os pontos cruciais de um design orientado a objetos. Uma classe é uma definição de uma estrutura que contém propriedades (variáveis) e métodos (funções). Classes são definidas com a palavra-chave class:

----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------

class Pessoa{
  public $nome = '';

  function nome($novo_nome = NULL){
    if(!is_null($novo_nome)){
      $this->nome = $novo_nome;
    }
    
    return $this->nome;
  }
}

Uma vez que uma classe é definida, qualquer número de objetos podem ser construídos a partir dela por meio do uso da palavra-chave new, e as propriedades e métodos do objeto podem ser acessadas com a construção ->. Veja:

----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------

  $pessoa = new Pessoa;
  $pessoa->nome('Osmar J. Silva');
  printf("Olá, %s<br>", $pessoa->nome);

Se quisermos saber se uma variável é do tipo object, podemos usar a função is_object(). Veja:

----------------------------------------------------------------------
Se precisar de ajuda com o código abaixo, pode me chamar
no WhatsApp +55 (62) 98553-6711 (Osmar)
----------------------------------------------------------------------

<?  
  class Pessoa{
    public $nome = '';

    function nome($novo_nome = NULL){
      if(!is_null($novo_nome)){
        $this->nome = $novo_nome;
      }
    
      return $this->nome;
    }
  }
  
  $pessoa = new Pessoa;

  if(is_object($pessoa)){
    echo 'A variável $pessoa é do tipo object.';
  }
?>

Ao executarmos este código PHP nós teremos o seguinte resultado:

A variável $pessoa é do tipo object.

Nossas 20 dicas & truques de programação mais populares

C# - Como testar se uma CheckBox do C# Windows Forms está marcada ou desmarcada

C++ - Como calcular fatorial em C++ usando recursividade

VB.NET - Como inverter o conteúdo de uma string em VB.NET usando os métodos ToCharArray() e Reverse()

C++ - Exercício Resolvido de C++ - Escreva um programa que solicite dois números do tipo inteiro distintos ao usuário e que apresente na tela o maior deles

JavaScript - Como retornar apenas os três primeiros elementos de um array em JavaScript usando a função slice() do objeto Array

C - Como concatenar apenas parte de uma string à outra string usando a função strncat() da linguagem C

C# - Como retornar o item selecionado em um ComboBox do C# Windows Forms usando a propriedade SelectedItem

Python - Datas e horas em Python - Como obter o nome do dia da semana no formato longo (segunda-feira, terça-feira, etc) usando a função strftime() do Python

Dart - Exercício Resolvido de Dart - Escreva um programa Dart para mover todos os zeros para o final do vetor, sem alterar a ordem dos elementos já presentes no array

JavaScript - Como retornar o ano com quatro dígitos em JavaScript usando a função getFullYear() do objeto Date - Datas e horas em JavaScript

Java - Como criar um programa de visualização de imagens em Java - Código fonte completo

VB.NET - Como calcular a equação reduzida da reta em VB.NET dados dois pontos pertencentes à reta

Python - Como formatar valores de ponto-flutuante com uma determinada quantidade de zeros à esquerda em Python

Java - Como obter o valor de PI em Java usando a constante Math.PI

Java - Java ArrayList - Como remover uma faixa de elementos de uma ArrayList simulando a função removeRange() do Java

C# - Como retornar o nome de um arquivo sem a extensão em C# usando o método GetFileNameWithoutExtension() da classe Path

C - Exercício Resolvido de C - Usando um laço for para percorrer os elementos de uma matriz e exibí-los na ordem original e invertida

C++ - Como renomear um diretório em C++ usando a função rename()

Excel - Como converter graus em radianos no Excel usando a função RADIANOS() - Trigonometria no Excel

Java - Curso Completo de Java - Como usar constantes em Java

Você também poderá gostar das dicas e truques de programação abaixo

JavaScript - Como retornar a diferença em dias entre duas datas usando JavaScript

Java - Java para iniciantes - Como controlar a quantidade de casas decimais na exibição de um valor double ou float

Java - Como criar uma fila em Java usando a interface Queue

Java - Java Swing - Como adicionar um JPopupMenu a um JTextArea

Java - Sistema para Biblioteca usando Programação Orientada a Objetos em Java - Projeto completo com código fonte - Versão console

Delphi - Como calcular o comprimento da hipotenusa em Delphi dadas as medidas do cateto oposto e do cateto adjascente

Java - Como usar o gerenciador de layout GridBagLayout em suas aplicações Java Swing

Delphi - Computação gráfica em Delphi - Como desenhar linhas usando o método LineTo() da classe TCanvas do Delphi

Python - Como exibir a data atual em Python de acordo com as configurações regionais usando as funções strftime() e setlocale()

JavaScript - Como ordenar um array de strings em ordem alfabética em JavaScript - Vetores e matrizes em JavaScript

Java - Como construir uma data no passado ou futuro em Java usando a classe GregorianCalendar

Java - Java para iniciantes - Como usar o laço do-while da linguagem Java

Python - Como converter uma string para float ou double em Python usando a função float()

Java - Exercício Resolvido de Java - Escreva um programa Java que efetue a soma dos elementos da diagonal principal de uma matriz

C - Como testar múltiplas condições usando a construção if...else if...else da linguagem C

Java - Exercícios Resolvidos de Java - Métodos - Um método estático que recebe um vetor de inteiros e o exibe

Python - E-Book 650 Dicas, Truques e _Exercícios Resolvidos_ de Python - PDF com 1.200 páginas

Revit Python Shell - Como copiar grupos no Revit usando a função Create.PlaceGroup() e o Revit Python Shell

C - Exercício Resolvido de C - Como calcular o restante de um salário após o pagamento de duas contas com juros

Python - Como remover e retornar um item aleatório em uma lista Python usando a função pop() e um número randômico

Nossas 20 dicas & truques de programação mais recentes

Python - Código completo para um visualizador de fotos e imagens em PyQt - Carregar imagens com botões de próxima imagem e imagem anterior

Python - Como calcular a previsão de cargas de iluminação em instalações elétricas residenciais usando Python - Python para Instalações Elétricas Prediais

C++ - Exercício Resolvido de C++ - Escreva um programa C++ para alocar dinamicamente um inteiro, um caractere e uma string

Excel VBA - Como usar o evento Worksheet_Change do Excel VBA para detectar a linha e a coluna da célula que foi modificada

Python - Como criar um programa de desenho de linhas no estilo AutoCAD usando PyQt

Python - Como desenhar um ponto na janela principal de uma aplicação PyQt usando a função drawPoint() da classe QPainter

Java - Exercícios Resolvidos de Java - Uma pousada estipulou o preço para a sua diária em R$ 30,00 e mais uma taxa de serviços diários de

Portugol - Exercícios Resolvidos de Portugol - Uma pousada estipulou o preço para a sua diária em R$ 30,00 e mais uma taxa de serviços diários de

Python - Cálculo de estribos em vigas de concreto armado usando Python - Armadura mínima transversal normativa

VBA - Como adicionar dias à data atual em VBA usando a função DateAdd() - Datas e horas em VBA

VBA - Como exibir a data e hora atual em VBA usando a função Now() - Datas e horas em VBA

VBA - Como exibir a data atual em VBA usando a função Date - Datas e horas em VBA

VBA - Como usar o laço de repetição For Next em nossas aplicações VBA

VBA - Como extrair uma substring à direita de uma string em VBA usando a função Right()

VBA - Como extrair uma substring à esquerda de uma string em VBA usando a função Left()

Python - Cálculo de estribos em vigas de concreto armado usando Python - Verificação da compressão diagonal do concreto

Excel - Como gerar números aleatórios inteiros entre 1 e 10 no Excel usando as funções ALEATÓRIO() e INT()

Excel - Como gerar números aleatórios no Excel usando a função ALEATÓRIO() - Excel para Matemática e Estatística

Python - Como gerar valores igualmente espaçados em Python sem o uso de bibliotecas externas

Java - Como gerar valores igualmente espaçados em Java sem o uso de bibliotecas externas

Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site

Python - Como criar uma Agenda de Contatos em Python + MySQL - Projeto completo com código fonte - Versão console

Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado

Java - Como criar o jogo Pedra, Papel, Tesoura em Java - Jogo completo em Java com código comentado

Java - Como criar um Jogo da Velha em Java - Jogo completo com código fonte comentado - Versão console

PHP - Software de Gestão Financeira com código fonte em PHP, MySQL, Bootstrap, jQuery - Inclui cadastro de clientes, fornecedores e ticket de atendimento

PHP - Calendário de Eventos em PHP e MySQL - Código fonte completo com opções de cadastrar, listar, excluir, editar e listar eventos

PHP - Como criar um Cadastro de Usuários em PHP e MySQL - Cadastrar, Listar, Editar, Exluir e Pesquisar - Código fonte completo

Java - Sistema para Biblioteca usando Programação Orientada a Objetos em Java - Projeto completo com código fonte - Versão console

Java - Simulação de Sistema Bancário usando Programação Orientada a Objetos em Java - Projeto completo com código fonte - Versão console

PHP - Controle de Estoque completo com código fonte em PHP, MySQL, Bootstrap, jQuery - 100% funcional e fácil de modificar e implementar novas funcionalidades

Últimos Exercícios Resolvidos

C++ - Exercício Resolvido de C++ - Escreva um programa C++ para alocar dinamicamente um inteiro, um caractere e uma string

Java - Exercícios Resolvidos de Java - Uma pousada estipulou o preço para a sua diária em R$ 30,00 e mais uma taxa de serviços diários de

Portugol - Exercícios Resolvidos de Portugol - Uma pousada estipulou o preço para a sua diária em R$ 30,00 e mais uma taxa de serviços diários de

Portugol - Exercícios Resolvidos de Portugol - Sabe-se que a Camiseteria Kanashiro está com uma promoção de camisetas nos seguintes tamanhos e valores

Python - Exercício Resolvido de Python - Calcular o número de Reynolds e identificar se o escoamento é liminar ou turbulento sabendo-se que em uma tubulação com diâmetro de 40 mm

Java - Exercícios Resolvidos de Java - Escreva um programa Java que cria um objeto da classe Calendar para a data e hora atual e mostre os valores máximos para o ano, mês, dia e semana

Java - Exercícios Resolvidos de Java - Escreva um programa Java que construa um objeto da classe Calendar representando a data e hora atual e mostre os valores individuais de ano, mês, dia

Java - Exercícios Resolvidos de Java - Escreva um programa Java que pede para o usuário informar o dia, mês e ano e construa uma data usando um objeto da classe Calendar

C - Exercícios Resolvidos de C - Escreva um programa C que peça para o usuário informar um ano e informe o dia da semana que o ano começou (domingo, segunda-feira

C - Exercícios Resolvidos de C - Escreva um programa C que informa o número de dias em um determinado mês e ano. Seu código deverá solicitar ao usuário o número correspondente

Java - Exercícios Resolvidos de Java - Escreva um programa Java que pede para o usuário informar sua data de nascimento e mostre a idade em anos, meses e dias

Java - Exercícios Resolvidos de Java - Escreva um programa Java que mostre a data atual e a data que será daqui a 10 dias, ou seja, a data atual acrescida de 10 dias

Portugol - Exercícios Resolvidos de Portugol - Escreva um programa Portugol para mover todos os zeros para o final do vetor, sem alterar a ordem dos elementos já presentes no array

VisuAlg - Exercícios Resolvidos de VisuAlg - Um programa que lê duas notas, calcula a média aritmética e exibe uma mensagem de reprovado, exame ou aprovado

Portugol - Exercícios Resolvidos de Portugol - Um programa que lê duas notas, calcula a média aritmética e exibe uma mensagem de reprovado, exame ou aprovado

Python - Exercícios Resolvidos de Python - Faça um programa que leia a idade e o sexo de 5 pessoas, mostrando no final: a) Quantos homens foram cadastrados

Python - Exercícios Resolvidos de Python - Escreva um programa Python que pergunte a velocidade de um carro. Caso ultrapasse 80km/h, exiba uma mensagem dizendo que

C++ - Exercícios Resolvidos de C++ - Escreva um programa C++ que pergunte a velocidade de um carro. Caso ultrapasse 80km/h, exiba uma mensagem dizendo que

C - Exercícios Resolvidos de C - Escreva um programa C que pergunte a velocidade de um carro. Caso ultrapasse 80km/h, exiba uma mensagem dizendo que

VisuAlg - Exercícios Resolvidos de VisuAlg - Escreva um programa VisuAlg que pergunte a velocidade de um carro. Caso ultrapasse 80km/h, exiba uma mensagem dizendo que

E-Books em PDF

E-Book 350 Exercícios Resolvidos de Java - PDF com 500 páginas

Domine lógica de programação e a linguagem Java com o nosso E-Book 350 Exercícios Exercícios de Java, para você estudar onde e quando quiser.

Este e-book contém exercícios resolvidos abrangendo os tópicos: Java básico, matemática e estatística, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.

Ver Conteúdo do E-book

E-Book 650 Dicas, Truques e Exercícios Resolvidos de Python - PDF com 1.200 páginas

Domine lógica de programação e a linguagem Python com o nosso E-Book 650 Dicas, Truques e Exercícios Exercícios de Python, para você estudar onde e quando quiser.

Este e-book contém dicas, truques e exercícios resolvidos abrangendo os tópicos: Python básico, matemática e estatística, banco de dados, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.

Ver Conteúdo do E-book

Linguagens Mais Populares

1º lugar: Java
2º lugar: Python
3º lugar: C#
4º lugar: PHP
5º lugar: C
6º lugar: Delphi
7º lugar: JavaScript
8º lugar: C++
9º lugar: VB.NET
10º lugar: Ruby

Python ::: Desafios e Lista de Exercícios Resolvidos ::: Engenharia Civil - Cálculo Estrutural

Exercícios Resolvidos de Python - Como calcular as reações de apoio, momento de flexão máxima e forças cortantes em uma viga bi-apoiada com carga distribuída retangular usando Python

GNU Octave ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas

Como calcular o coeficiente angular de uma reta em GNU Octave dados dois pontos no plano cartesiano

Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes)

Exercício Resolvido de Java - Desenvolva um programa que leia dez números do tipo inteiro ao usuário Armazene esses dez números em um vetor

PHP ::: Fundamentos da Linguagem ::: Tipos de Dados

Como usar o tipo de dados object da linguagem PHP

Questões de Concurso para Engenharia Civil

Exercícios Resolvidos

Bancos de Dados

Questões de Concurso

Frameworks

Projetos e Códigos Fonte

Especializações

Calculadoras

Ferramentas

Todas as Linguagens, Frameworks, Biliotecas e Bancos de Dados

Compre pelo WhatsApp: +55 (062) 98553-6711

E-Book 350 Exercícios Resolvidos de Java - Com comentários em Português

PDF COM 500 PÁGINAS

Apenas R$ 19,90