Você está aqui: Cards de Engenharia Civil - Fundações |
||
|
||
|
|
||
C++ ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como somar os elementos de um vetor de inteiros em C++Quantidade de visualizações: 17460 vezes |
Esta dica mostra a você como usar um laço for do C++ para somar todos os valores dos elementos de um vetor de inteiros. Observe que aqui nós declaramos e inicializamos o vetor (array) em apenas uma instrução:
#include <iostream>
using namespace std;
int main(int argc, char *argv[])
{
// declara e inicializa um array de
// 5 inteiros
int valores[] = {2, 7, 1, 5, 6};
int soma = 0;
// soma os valores dos elementos
for(int i = 0; i < 5; i++){
soma += valores[i];
// o mesmo que
// soma = soma + valores[i];
}
// exibe o resultado
cout << "Soma: " << soma << endl;
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
Ao executar este código C++ nós teremos o seguinte resultado: Soma: 21 |
Java ::: Estruturas de Dados ::: Pilhas |
Como criar uma pilha em Java usando um vetor (array) - Estruturas de Dados em JavaQuantidade de visualizações: 2871 vezes |
A Pilha é uma estrutura de dados do tipo LIFO - Last-In, First-Out (Último a entrar, primeiro a sair). Neste tipo de estrutura, o último elemento a ser inserido é o primeiro a ser removido. Veja a imagem a seguir: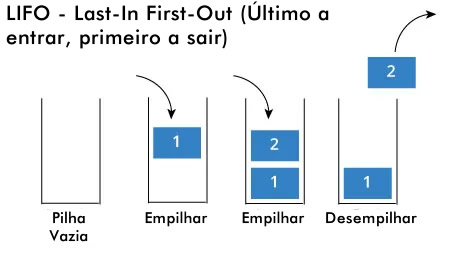 Embora seja mais comum a criação de uma estrutura de dados do tipo Pilha de forma dinâmica (usando ponteiros e referências), nesta dica eu mostrarei como podemos criá-la em Java usando um array, ou seja, um vetor. No exemplo eu usei inteiros, mas você pode modificar para o tipo de dados que você achar mais adequado. Veja o código completo para uma classe Pilha usando um vetor de ints. Veja que o tamanho do vetor é informado no construtor da classe. Note também a lógica empregada na construção dos métodos empilhar(), desempilhar() e imprimirPilha(): Código para Pilha.java:
package estudos;
public class Pilha {
private int elementos[]; // elementos na pilha
private int topo; // o elemento no topo da pilha
private int maximo; // a quantidade máxima de elementos na pilha
// construtor da classe Pilha
public Pilha(int tamanho) {
// constrói o vetor
this.elementos = new int[tamanho];
// define o topo como -1
this.topo = -1;
// ajusta o tamanho da pilha para o valor recebido
this.maximo = tamanho;
}
// método usado para empilhar um novo elemento na pilha
public void empilhar(int item) {
// a pilha já está cheia?
if (this.topo == (this.maximo - 1)) {
System.out.println("\nA pilha está cheia\n");
}
else {
// vamos inserir este elemento no topo da pilha
this.elementos[++this.topo] = item;
}
}
// méodo usado para desempilhar um elemento da pilha
public int desempilhar() {
// a pilha está vazia
if (this.topo == -1) {
System.out.println("\nA pilha está vazia\n");
return -1;
}
else {
System.out.println("Elemento desempilhado: " + elementos[topo]);
return this.elementos[this.topo--];
}
}
// método que permite imprimir o conteúdo da pilha
public void imprimirPilha() {
// pilha vazia
if (this.topo == -1) {
System.out.println("\nA pilha está vazia\n");
}
else {
// vamos percorrer todos os elementos da pilha
for (int i = 0; i <= this.topo; i++) {
System.out.println("Item[" + (i + 1) + "]: " + this.elementos[i]);
}
}
}
}
Veja agora o código para a classe principal, ou seja, a classe Main usada para testar a funcionalidade da nossa pilha: Código para Principal.java:
package estudos;
public class Estudos{
public static void main(String[] args){
// vamos criar uma nova pilha com capacidade para 5 elementos
Pilha p = new Pilha(5);
// vamos empilhar 3 elementos
p.empilhar(34);
p.empilhar(52);
p.empilhar(18);
// vamos mostrar os elementos na pilha
System.out.println("Itens presentes na Pilha\n");
p.imprimirPilha();
// agora vamos remover e retornar dois elementos da pilha
System.out.println();
p.desempilhar();
p.desempilhar();
// vamos mostrar os elementos na pilha novamente
System.out.println("\nItens presentes na Pilha\n");
p.imprimirPilha();
}
}
Ao executar este código Java nós teremos o seguinte resultado: Itens presentes na Pilha Item[1]: 34 Item[2]: 52 Item[3]: 18 Elemento desempilhado: 18 Elemento desempilhado: 52 Itens presentes na Pilha Item[1]: 34 |
Java ::: Coleções (Collections) ::: HashMap |
Java HashMap - Como fornecer uma chave e obter seu valor correspondente em um HashMapQuantidade de visualizações: 9495 vezes |
O uso de um HashMap só se justifica quando podemos guardar os mapeamentos e recuperá-los de forma rápida e fácil. Para isso, a classe HashMap nos fornece o método get(). Este método recebe a chave a ser pesquisada e retorna o valor associado a ela. Veja sua assinatura:public V get(Object key) Veja um exemplo no qual usamos o método get() para retornar o valor associado à chave informada:
package arquivodecodigos;
import java.util.*;
public class Estudos{
public static void main(String[] args){
// vamos criar uma instância de HashMap
HashMap<Integer, String> clientes = new HashMap<Integer, String>();
// vamos adicionar três chaves e seus valores
clientes.put(new Integer(1), "Osmar J. Silva");
clientes.put(new Integer(2), "Salvador Miranda de Andrade");
clientes.put(new Integer(3), "Marcos da Costa Santos");
// vamos obter o valor correspondente à chave 2
String c = clientes.get(2);
// vamos exibir o resultado
if(c != null){
System.out.println("O valor para esta chave é: " + c);
}
else{
System.out.println("O HashMap não contém a chave informada.");
}
System.exit(0);
}
}
Ao executarmos este código Java nós teremos o seguinte resultado: O valor para esta chave é: Salvador Miranda de Andrade |
JavaScript ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em JavaScript usando a função cos() do objeto Math - Calculadora de cosseno em JavaScriptQuantidade de visualizações: 7858 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da linguagem JavaScript. Esta função, que é parte do objeto Math, recebe um valor numérico e retorna um valor também numérico) entre -1 até 1 (ambos inclusos). Veja:
<html>
<head>
<title>Estudos JavaScript</title>
</head>
<body>
<script type="text/javascript">
// vamos calcular o cosseno de 3 números
document.writeln("Cosseno de 0 = " + Math.cos(0));
document.writeln("<br>Cosseno de 1 = " + Math.cos(1));
document.writeln("<br>Cosseno de 2 = " + Math.cos(2));
</script>
</body>
</html>
Ao executar este código JavaScript nós teremos o seguinte resultado: Cosseno de 0 = 1 Cosseno de 1 = 0.5403023058681398 Cosseno de 2 = -0.4161468365471424 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 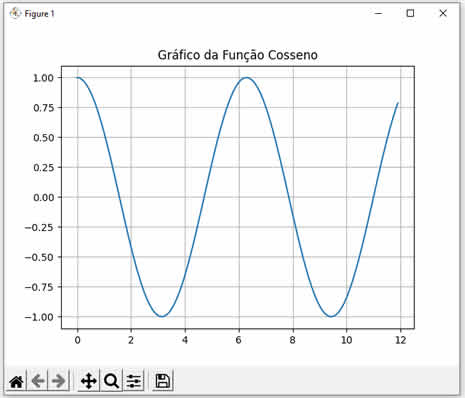 |
Dart ::: Dicas de Estudo e Anotações ::: Estruturas de Controle |
Como usar o laço while da linguagem DartQuantidade de visualizações: 2669 vezes |
|
O laço while (enquanto), ou loop while, é usado quando queremos repetir uma ou mais instruções ENQUANTO uma condição estiver sendo satisfeita. A condição para a execução desse laço é o retorno de uma condição true ou false. Veja um exemplo no qual usamos o laço while para contar de 0 até 10:
void main() {
int cont = 1;
while (cont < 10) {
print(cont);
cont++; // aumenta cont em 1
}
}
Este código, quando executado, gera o seguinte resultado: 1 2 3 4 5 6 7 8 9 É importante observar que um laço while pode nunca ser executado. Para isso basta que o teste condicional na entrada do laço retorne um resultado falso. Veja agora como usar um laço while para encontrar os 10 primeiros múltiplos de 5 e 7:
void main() {
int cont = 0;
int numero = 1;
// queremos encontrar 10 múltiplos de 5 e 7
while (cont < 10) {
if ((numero % 5 == 0) && (numero % 7 == 0)) {
print(numero);
cont++;
}
// incrementa o número
numero++;
}
}
Quando executamos este código nós obtemos o seguinte resultado: 35 70 105 140 175 210 245 280 315 350 |
Veja mais Dicas e truques de Dart |
Dicas e truques de outras linguagens |
|
JavaScript - Como testar se uma string termina com uma determinada substring em JavaScript usando a função endsWith() |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






