 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
JavaScript ::: Dicas & Truques ::: Miscelâneas |
JavaScript para iniciantes - Como usar o método escape() para codificar uma frase em JavaScriptQuantidade de visualizações: 12745 vezes |
|
A função escape() da linguagem JavaScript é usada quando precisamos codificar uma palavra, frase ou texto, ou seja, uma string. Em geral nós a usamos para codificar caracteres especiais em uma string, com a exceção dos caracteres e símbolos "* @ - _ + . /". Veja um exemplo completo:
<html>
<head>
<title>Estudando JavaScript</title>
</head>
<body>
<script type="text/javascript">
var frase = "Programar em JavaScript é muito bom";
document.write("Original: " + frase + "<br>");
document.write("Codificada: " + escape(frase));
</script>
</body>
</html>
Ao executarmos este código nós teremos o seguinte resultado: Original: Programar em JavaScript é muito bom Codificada: Programar%20em%20JavaScript %20%E9%20muito%20bom Lembre-se de que o objetivo da função escape() é tornar uma string portável, ou seja, que pode ser transmitida pela rede para qualquer computador que suportar os caracteres ASCII. Nota: A função escape() foi marcada como desatualizada (deprecated) a partir do JavaScript 1.5. Em vez dela nós devemos usar as funções encodeURI() ou encodeURIComponent(). |
Java ::: Dicas & Truques ::: Strings e Caracteres |
Como contar as ocorrências de uma substring em uma string do Java usando o método substring() e um laço forQuantidade de visualizações: 1 vezes |
|
Nesta dica mostrarei como podemos usar o método substring() da classe String, combinado com o laço for, para contar as ocorrências de uma substring em uma string da linguagem Java. Note que usamos também os métodos length() e equals() para completar a tarefa. Veja o código Java completo para o exemplo:
package estudos;
public class Estudos{
public static void main(String[] args){
// vamos criar uma string representando uma frase
String frase = "Programar em Java só é melhor que programar em Java";
// a substring que vamos pesquisar
String sub = "Java"; // ocorrências de "Java"
// quantidade de ocorrências
int cont = 0;
// um laço for que vai de 0 até o tamanho da primeira string menos
// o tamanho da segunda string - 1
for(int i = 0; i < (frase.length() - sub.length() + 1); i++){
String res = frase.substring(i, (i + sub.length()));
// encontramos a substring mais uma vez?
if(res.equals(sub)){
cont++;
}
}
System.out.println("A frase contém " + cont + " ocorrências de " + sub);
// fecha o programa
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: A frase contém 2 ocorrências de Java |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Java Básico |
Exercícios Resolvidos de Java - Um programa que lê um salário e concede um aumento de 20% para os salários inferiores a R$ 800,00Quantidade de visualizações: 4877 vezes |
|
Exercícios Resolvidos de Java - Um programa que lê um salário e concede um aumento de 20% para os salários inferiores a R$ 800,00 Pergunta/Tarefa: A empresa XYZ decidiu conceder um aumento de 20% aos funcionários com salários inferiores a R$ 800,00. Faça um programa Java que solicita o salário do funcionário e mostre o valor do salário reajustado ou uma mensagem, caso o funcionário não tenha direito ao aumento. Sua saída deverá ser parecida com: Informe o salário: 520 O salário informado foi: 520.0 O salário reajustado é: 530.4 Veja a resolução comentada deste exercício usando Java:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
Scanner entrada = new Scanner(System.in);
// vamos solicitar o salário do funcionário
System.out.print("Informe o salário: ");
double salario = Double.parseDouble(entrada.nextLine());
System.out.println("O salário informado foi: " + salario);
// vamos conceder o aumento ao salário inferior a 800,00
if(salario < 800.00){
double novoSalario = salario + (salario * (2.0 / 100.00));
System.out.println("O salário reajustado é: " + novoSalario);
}
else{
System.out.println("Não tem direito ao reajuste.");
}
System.out.println("\n");
}
}
|
jQuery ::: Dicas & Truques ::: Manipulação e Conteúdo Dinâmico |
Como adicionar conteúdo ao início de um elemento HTML usando a função prepend() do jQueryQuantidade de visualizações: 599 vezes |
|
O método prepend() permite adicionar conteúdo ao início de um elemento HTML. Este conteúdo pode ser um seletor, um elemento HTML, uma string HTML ou um objeto jQuery. Veja um trecho de código no qual adicionamos uma linha de texto no início de um parágrafo:
<script type="text/javascript">
<!--
function adicionarConteudo(){
var texto = "Mais uma linha.<br>";
$("#parag").prepend(texto);
}
//-->
</script>
O método prepend() opera em todos os elementos HTML retornados sob uma determinação condição. O retorno do método é um objeto jQuery que pode ser usado para fins de encadeamento de chamadas de métodos. |
VB.NET ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Como usar a instrução Exit para abandonar a execução de um laço em VB.NETQuantidade de visualizações: 10128 vezes |
|
A instrução Exit pode ser usada para alterar o fluxo de controle de um programa. Há várias formas de instrução Exit, cada uma apropriada para sair (abandonar) a execução de diferentes tipos de blocos de códigos. Esta dica mostra como usar a instrução Exit para abandonar a execução dos laços Do While...Loop, Do...Loop While, Do Until...Loop, Do...Loop Until, For...Next e While. Em cada um destes laços, a instrução Exit deve vir acompanhada do nome do laço. Veja um exemplo:
Dim numero As Integer = 1
While numero <= 100
Console.WriteLine(numero)
numero += 1
If numero > 20 Then
Exit While
End If
End While
Execute este código e veja que a contagem pára no 20. Vejamos agora um exemplo do uso da instrução Exit com um laço For...Next:
For valor As Integer = 3 To 100 Step 3
Console.WriteLine(valor)
If valor > 20 Then
Exit For
End If
Next
Execute e veja como o laço é interrompido quando o valor da variável valor se torna maior que 20. Para finalizar, lembre-se de que a instrução Exit abandona a execução do laço no local exata em que esta é inserida. Tenha isso em mente para evitar efeitos indesejados em seus códigos. |
Revit C# ::: Dicas & Truques ::: Eixos - Grids |
Como criar eixos no Revit via programação usando a função Create() da classe Grid da Revit C# APIQuantidade de visualizações: 401 vezes |
|
Os eixos, ou grids, são linhas que auxiliam na construção de um projeto, ou seja, uma espécie de malha de linhas. Eles são mais utilizados quando se trabalha com elementos estruturais, para a locação de colunas e pilares. No Revit, os eixos podem ser verticais, horizontais, inclinados e até em forma de arcos. Para criá-los, vá na aba Arquitetura, seção Dados e localize o item Eixo (ou digite GR). Via programação nós podemos criar um eixo no Revit usando a função Create() da classe Grid da Revit C# API. Neste exemplo mostrarei, em detalhes, como isso pode ser feito. O primeiro passo é obter uma referência ao documento UI atual usando this.ActiveUIDocument. Após isso acessar o documento usando uidoc.Document. As coordenadas geométricas de início e fim do eixo são criadas como objetos da classe XYZ. Então, de posse das coordenadas, nós criamos um objeto Line usando a função Line.CreateBound(). Para finalizar nós usamos a função Grid.Create() para desenhar o eixo na área de desenho do Revit. Note como passamos o objeto Line e uma referência ao documento atual para esta função. Veja ainda o uso de uma Transaction para abrir uma transação do Revit, criar o elemento e fechá-la em seguida. Este exemplo criará um eixo com o LevelId -1, ou seja, no primeiro nível do documento. Em outras dicas dessa seção eu mostro como definir o nível para o grid recém-criado. Veja o código Revit C# API completo para o exemplo:
using System;
using System.Collections.Generic;
using System.IO;
using System.Linq;
using Autodesk.Revit.DB;
using Autodesk.Revit.DB.Architecture;
using Autodesk.Revit.DB.Structure;
using Autodesk.Revit.UI;
using Autodesk.Revit.UI.Selection;
namespace Estudos {
[Autodesk.Revit.Attributes.Transaction(Autodesk.Revit.Attributes.
TransactionMode.Manual)]
[Autodesk.Revit.DB.Macros.AddInId("ED8EC6C4-9489-48F7-B04E-B45B5D1BEB12")]
public partial class ThisApplication {
private void Module_Startup(object sender, EventArgs e) {
// primeiro obtemos uma referência ao documento atual
UIDocument uidoc = this.ActiveUIDocument;
Document doc = uidoc.Document;
// criamos a linha geométrica para posicionar o eixo
// não se esqueça de converter metros para pés
XYZ inicio = new XYZ(0, -100, 0);
XYZ final = new XYZ(0, 100, 0);
// construímos a linha
Line linhaGeometrica = Line.CreateBound(inicio, final);
// iniciamos uma nova transação
using(Transaction t= new Transaction(doc)) {
t.Start("Criar um novo Grid");
// e criamos o novo eixo
Grid eixo = Grid.Create(doc, linhaGeometrica);
t.Commit();
// e mostramos o resultado
TaskDialog.Show("Aviso", "O novo eixo foi criado com o ID: " +
eixo.Id);
}
}
private void Module_Shutdown(object sender, EventArgs e) {
// para fazer alguma limpeza de memória ou algo assim
}
#region Revit Macros generated code
private void InternalStartup() {
this.Startup += new System.EventHandler(Module_Startup);
this.Shutdown += new System.EventHandler(Module_Shutdown);
}
#endregion
}
}
Ao executar este código Revit C# API teremos o seguinte resultado: O novo eixo foi criado com o ID: 49827 |
C# ::: Dicas & Truques ::: Matemática e Estatística |
Como testar se um número é primo em C#Quantidade de visualizações: 7868 vezes |
|
O Número Primo é o número maior que 1 e que só pode ser dividido por 1 e por ele mesmo, ou seja, números primos não podem ser divididos por outros números, a não ser por ele mesmo e pelo número 1. Dessa forma, 2, 3, 5, 7, 11, 13, 17, etc, são todos números primos. É importante observar que 0 e 1 não são números primos, e que o número 2 é o único número primo par. Veja agora um código C# completo que pede para o usuário informar um número inteiro positivo e mostra uma mensagem indicando se o número informado é primo ou não:
using System;
namespace Estudos {
class Program {
static void Main(string[] args) {
bool primo = true;
// vamos solicitar um número inteiro positivo
Console.Write("Informe um número inteiro positivo: ");
int numero = int.Parse(Console.ReadLine());
// o número é negativo?
if (numero < 0) {
Console.WriteLine("Número inválido.");
}
// é 0 ou 1?
else if ((numero == 0) || (numero == 1)) {
Console.WriteLine("Número válido, mas não é primo.");
}
// passou até aqui. Vamos testar se o número é primo
else {
for (int i = 2; i <= (numero / 2); i++) {
// se passar no teste, não é primo
if (numero % i == 0) {
primo = false; // recebe false
break;
}
}
if (primo) {
Console.WriteLine("O número informado é primo");
}
else {
Console.WriteLine("O número informado não é primo");
}
}
Console.WriteLine("\n\nPressione qualquer tecla para sair...");
// pausa o programa
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Informe um número inteiro positivo: 9 O número informado não é primo |
Delphi ::: Imagens, Gráficos e Cores ::: TBitmap (A classe TBitmap) |
Computação gráfica em Delphi - Como usar a classe TBitmap do DelphiQuantidade de visualizações: 16704 vezes |
|
A classe TBitmap encapsula um bitmap Windows (HBITMAP, um handle para um bitmap), incluindo sua paleta (HPALETTE, um handle para uma paleta de cores). Esta classe herda de TGraphic e é usada para criar, manipular (redimensionar, rolar, rotacionar, pintar, etc) e armazenar imagens na memória e como arquivos em disco. A classe TBitmap contém muitas propriedades e métodos úteis. Entre seus métodos podemos citar LoadFromFile(), usado para carregar uma imagem bitmap a partir do disco e guardá-la em memória como um objeto TBitmap. Veja o trecho de código abaixo:
procedure TForm2.Button1Click(Sender: TObject);
var
bmp: TBitmap;
begin
// vamos criar o bitmap
bmp := TBitmap.Create;
// vamos carregar a imagem e guardá-la no bitmap
bmp.LoadFromFile('foto.bmp');
// vamos desenhar o bitmap no formulário
// começando nas coordenadas x = 0; y = 0 a partir
// do canto superior esquerdo da área cliente do formulário
Form2.Canvas.Draw(0, 0, bmp);
// vamos liberar o bitmap
bmp.Free;
end;
Aqui nós carregamos o bitmap foto.bmp e o desenhamos na superfície do formulário usando o método Draw() do Canvas do formulário. É possível também redimensionar o bitmap ao desenhá-lo no formulário. Veja este novo trecho de código:
procedure TForm2.Button1Click(Sender: TObject);
var
bmp: TBitmap;
retang: TRect; // um objeto TRect
begin
// vamos criar o bitmap
bmp := TBitmap.Create;
// vamos carregar a imagem e guardá-la no bitmap
bmp.LoadFromFile('foto.bmp');
// vamos redimensionar o bitmap na memória de
// acordo com o retângulo abaixo
retang.Top := 0;
retang.Left := 0;
retang.Right := 200;
retang.Bottom := 150;
// vamos desenhar o bitmap usando o método
// StretchDraw da classe TCanvas
Form2.Canvas.StretchDraw(retang, bmp);
// vamos liberar o bitmap
bmp.Free;
end;
Aqui nós usamos um objeto do registro (record) TRect para criar um retângulo especificando o tamanho do bitmap e fornecemos tal retângulo, juntamente com o bitmap, para o método StretchDraw() da classe TCanvas. Este método redimensiona a imagem antes de desenhá-la na superfície do formulário. Para fins de compatibilidade, esta dica foi escrita usando Delphi 2009. |
TypeScript ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em TypeScript dados dois pontos no plano cartesianoQuantidade de visualizações: 1525 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem TypeScript que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
// x e y do primeiro ponto
var x1:number = 3;
var y1:number = 6;
// x e y do segundo ponto
var x2:number = 9;
var y2:number = 10;
var m:number = (y2 - y1) / (x2 - x1);
// mostramos o resultado
console.log("O coeficiente angular é: " + m);
Ao executar este código TypeScript nós teremos o seguinte resultado: O coeficiente angular é: 0.6666666666666666 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
// x e y do primeiro ponto
var x1:number = 3;
var y1:number = 6;
// x e y do segundo ponto
var x2:number = 9;
var y2:number = 10;
// vamos obter o comprimento do cateto oposto
var cateto_oposto:number = y2 - y1;
// e agora o cateto adjascente
var cateto_adjascente:number = x2 - x1;
// vamos obter o ângulo tetha, ou seja, a inclinação da hipotenusa
// (em radianos, não se esqueça)
var tetha:number = Math.atan2(cateto_oposto, cateto_adjascente);
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
var tangente:number = Math.tan(tetha);
// mostramos o resultado
console.log("O coeficiente angular é: " + tangente);
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Java ::: Java para Engenharia ::: Eletricidade, Circuitos Elétricos e Eletrônicos |
Como calcular corrente, voltagem, resistência e potência em um circuito série de corrente contínua usando JavaQuantidade de visualizações: 2074 vezes |
|
Como calcular corrente, voltagem, resistência e potência em um círcuito série de corrente contínua usando Java Nesta dica mostrarei como é possível usar operações básicas da linguagem Java para calcular a corrente, voltagem, resistência e potência em um circuito série de corrente contínua. É conhecido como um circuito série um circuito composto exclusivamente por componentes elétricos ou eletrônicos conectados em série (de conexão em série, que é o mesmo que associação em série ou ligação em série). A associação em série é uma das formas básicas de se conectarem componentes elétricos ou eletrônicos. A nomeação descreve o método como os componentes são conectados. Vanos começar analisando a seguinte imagem: 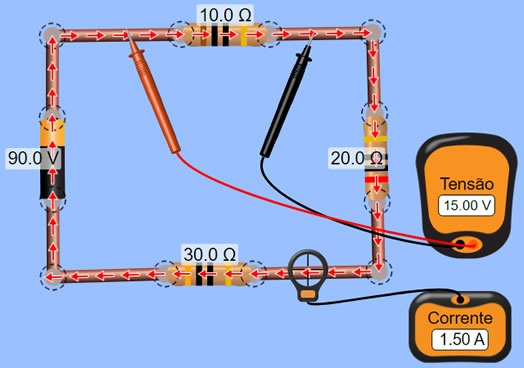 Esta imagem foi extraída do Simulador do PHET, no endereço https://phet.colorado.edu. Note que temos uma fonte de alimentação 90V, e três resistores (com resistências de 10Ω, 20Ω e 30Ω). Vamos começar relembrando os aspectos importantes dos circuitos em série: 1) A corrente elétrica I (medida em ampères (A), ou coulombs por segundo) é comum a todos os elementos do circuito. 2) A tensão elétrica V, (medida em volts (V), ou joules por coulomb) é dividida entre as cargas, ou seja, a soma das tensões nas cargas deve ser igual à tensão da fonte de alimentação. 3) A resistência elétrica R (medida em ohms (Ω)) total do circuito é igual à soma de todas as resistências das cargas. 4) A potência total P (medida em watts (W)) é igual à soma das potências das cargas que compõem o circuito. Vamos escrever um pouco de código então? Veja nosso primeiro código Java que calcula a corrente total, a tensão total, a resistência total e a potência total do circuito em série mostrado na imagem:
package estudos_java;
public class Estudos{
public static void main(String[] args){
// Tensão total do circuito em série
double eTotal = 90.0;
// Resitência total
double resist1 = 10.0;
double resist2 = 20.0;
double resist3 = 30.0;
double rTotal = resist1 + resist2 + resist3;
// Corrente elétrica total
double iTotal = eTotal / rTotal;
// Potência elétrica total
double pTotal = eTotal * iTotal;
// mostra os valores
System.out.println("Tensão total: " + eTotal);
System.out.println("Resistência total: " + rTotal);
System.out.println("Corrente total: " + iTotal);
System.out.println("Potência total: " + pTotal);
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Tensão total: 90.0 Resistência total: 60.0 Corrente total: 1.5 Potência total: 135.0 Pronto! Agora que já sabemos o valor da corrente elétrica, e sabemos que a corrente é comum a todos os elementos do circuito em série, podemos calcular a tensão individual dos componentes. Assim, veja um trecho de código Java que calcula a tensão elétrica nos três resistores (lembre-se: tensão é o produto da corrente pela resistência):
package estudos_java;
public class Estudos{
public static void main(String[] args){
// Tensão total do circuito em série
double eTotal = 90.0;
// Resitência total
double resist1 = 10.0;
double resist2 = 20.0;
double resist3 = 30.0;
double rTotal = resist1 + resist2 + resist3;
// Corrente elétrica total
double iTotal = eTotal / rTotal;
// Potência elétrica total
double pTotal = eTotal * iTotal;
// mostra os valores
System.out.println("Tensão total: " + eTotal);
System.out.println("Resistência total: " + rTotal);
System.out.println("Corrente total: " + iTotal);
System.out.println("Potência total: " + pTotal);
// mostra as tensões nos resistores
System.out.println("\nTensão nos resistores individuais:");
double e1 = resist1 * iTotal;
double e2 = resist2 * iTotal;
double e3 = resist3 * iTotal;
System.out.println("Tensão no Resistor 1: " + e1 + "V");
System.out.println("Tensão no Resistor 2: " + e2 + "V");
System.out.println("Tensão no Resistor 3: " + e3 + "V");
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Tensão total: 90.0 Resistência total: 60.0 Corrente total: 1.5 Potência total: 135.0 Tensão nos resistores individuais: Tensão no Resistor 1: 15.0V Tensão no Resistor 2: 30.0V Tensão no Resistor 3: 45.0V Para finalizar, vamos calcular a potência dissipada em cada um dos resistores de forma individual. Observe que a potência é o produto da tensão pela corrente (P = E.I). Eis o código:
package estudos_java;
public class Estudos{
public static void main(String[] args){
// Tensão total do circuito em série
double eTotal = 90.0;
// Resitência total
double resist1 = 10.0;
double resist2 = 20.0;
double resist3 = 30.0;
double rTotal = resist1 + resist2 + resist3;
// Corrente elétrica total
double iTotal = eTotal / rTotal;
// Potência elétrica total
double pTotal = eTotal * iTotal;
// mostra os valores
System.out.println("Tensão total: " + eTotal);
System.out.println("Resistência total: " + rTotal);
System.out.println("Corrente total: " + iTotal);
System.out.println("Potência total: " + pTotal);
// mostra as tensões nos resistores
System.out.println("\nTensão nos resistores individuais:");
double e1 = resist1 * iTotal;
double e2 = resist2 * iTotal;
double e3 = resist3 * iTotal;
System.out.println("Tensão no Resistor 1: " + e1 + "V");
System.out.println("Tensão no Resistor 2: " + e2 + "V");
System.out.println("Tensão no Resistor 3: " + e3 + "V");
// mostra as potências dissapadas nos resistores
System.out.println("\nPotência dissipada nos resistores individuais:");
double p1 = e1 * iTotal; // Potência = Tensão x Corrente
double p2 = e2 * iTotal;
double p3 = e3 * iTotal;
System.out.println("Potência no Resistor 1: " + p1 + "W");
System.out.println("Potência no Resistor 2: " + p2 + "W");
System.out.println("Potência no Resistor 3: " + p3 + "W");
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Tensão total: 90.0 Resistência total: 60.0 Corrente total: 1.5 Potência total: 135.0 Tensão nos resistores individuais: Tensão no Resistor 1: 15.0V Tensão no Resistor 2: 30.0V Tensão no Resistor 3: 45.0V Potência dissipada nos resistores individuais: Potência no Resistor 1: 22.5W Potência no Resistor 2: 45.0W Potência no Resistor 3: 67.5W |
Nossas 20 dicas & truques de programação mais populares |
|
PHP - Programação Orientada a Objetos em PHP - Aprenda a criar e usar métodos e classes abstratas em PHP Delphi - Como usar a propriedade Eof para verificar se estamos no último registro do TClientDataSet do Delphi |
Você também poderá gostar das dicas e truques de programação abaixo |
|
React.js - Aprenda a desenvolver aplicações React diretamente no HTML, sem usar a ferramenta create-react-app |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





