 |
|
||||
Você está aqui: Java ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular a área de um círculo em Java dado o raio do círculoQuantidade de visualizações: 37071 vezes |
A área de um círculo pode ser calculada por meio do produto entre a constante PI e a medida do raio ao quadrado (r2). Comece analisando a figura abaixo: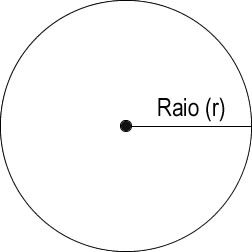 Sendo assim, temos a seguinte fórmula:  Onde A é a área, PI equivale a 3,14 (aproximadamente) e r é o raio do círculo. O raio é a medida que vai do centro até um ponto da extremidade do círculo. O diâmetro é a medida equivalente ao dobro da medida do raio, passando pelo centro do círculo e dividindo-o em duas partes. A medida do diâmetro é 2 * Raio. Veja agora um código Java completo que calcula a área de um círculo mediante a informação do raio:
package arquivodecodigos;
import java.util.Scanner;
public class Estudos{
public static void main(String[] args){
double area, raio;
Scanner in = new Scanner(System.in);
System.out.print("Informe o raio do círculo: ");
raio = Float.parseFloat(in.nextLine());
Ao executarmos este código nós teremos o seguinte resultado: Informe o raio do círculo: 5 A area do círculo de raio 5.0 é igual a 78.53981633974483 A circunferência é um conjunto de pontos que estão a uma mesma distância do centro. Essa distância é conhecida como raio. A circunferência é estudada pela Geometria Analítica e, em geral, em um plano cartesiano. O círculo, que é formado pela circunferência e pelos infinitos pontos que preenchem seu interior, é estudado pela Geometria Plana, pois ele ocupa um espaço e pode ter sua área calculada, diferentemente da circunferência. |
 Link para compartilhar na Internet ou com seus amigos: |
Desafios, Exercícios e Algoritmos Resolvidos de Java |
Veja mais Dicas e truques de Java |
Dicas e truques de outras linguagens |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |
