 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
PHP ::: Dicas & Truques ::: Arquivos e Diretórios |
Como verificar se um arquivo existe usando a função file_exists() do PHPQuantidade de visualizações: 13033 vezes |
|
Em algumas situações nós precisamos verificar a existência de um arquivo ou diretório no sistema de arquivos de um determinado site. Para isso nós podemos usar a função file_exists() da linguagem PHP. Esta função retorna um valor true se o arquivo ou diretório existir no caminho especificado, e false em caso contrário. Veja um exemplo completo de seu uso:
<?php
// pesquisa no diretório atual
$arquivo = "testes.txt";
if(file_exists($arquivo)){
echo "O arquivo já existe.";
}
else{
echo "O arquivo não existe ainda.";
}
?>
Ao executar este código PHP nós teremos o seguinte resultado: O arquivo já existe. |
Ruby ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em Ruby usando o método cos() da biblioteca Math - Calculadora de cosseno em RubyQuantidade de visualizações: 960 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da linguagem Ruby. Esta método, que faz parte da biblioteca Math, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja: puts "Cosseno de 0 = " + Math.cos(0).to_s puts "Cosseno de 1 = " + Math.cos(1).to_s puts "Cosseno de 2 = " + Math.cos(2).to_s Ao executar este código Ruby nós teremos o seguinte resultado: Cosseno de 0 = 1.0 Cosseno de 1 = 0.5403023058681398 Cosseno de 2 = -0.4161468365471424 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 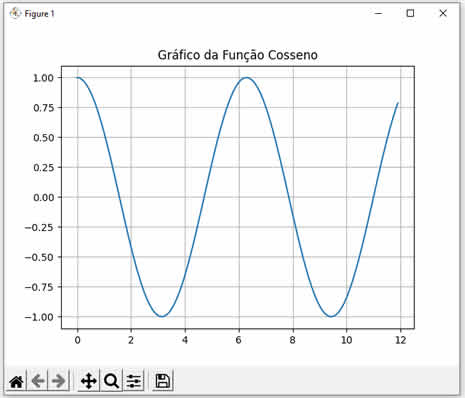 |
Python ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como converter graus em radianos em Python - Trigonometria em PythonQuantidade de visualizações: 3166 vezes |
|
Quando estamos trabalhando com trigonometria na linguagem Python, é importante ficarmos atentos ao fato de que todos os métodos e funções trigonométricas em Python recebem seus argumentos em radianos, em vez de graus. Nesta dica veremos como converter graus em radianos (sem a chatice de ficar relembrando regra de três). Veja a fórmula abaixo: \[Radianos = Graus \times \frac{\pi}{180}\] Agora veja como esta fórmula pode ser escrita em código Python:
import math
# função principal do programa
def main():
# valor em graus
graus = 30
# obtém o valor em radianos
radianos = graus * (math.pi / 180)
# mostra o resultado
print(graus, "graus convertidos para",
"radianos é", radianos)
if __name__== "__main__":
main()
Ao executarmos este código Python nós teremos o seguinte resultado: 30 graus convertidos para radianos é 0.5235987755982988 Por fim, saiba que a linguagem Python nos oferece o método math.radians() que nos permite converter ângulos em graus para radianos. Meu propósito nesta dica foi mostrar a você como o cálculo de conversão pode ser escrito em Python. Em outras dicas dessa seção abordaremos o método math.radians(). |
Java ::: Fundamentos da Linguagem ::: Tipos de Dados |
Como usar o tipo de dados char da linguagem JavaQuantidade de visualizações: 25494 vezes |
O tipo de dados char é usado para representar um único caractere. Veja:
public class Estudos{
public static void main(String args[]){
char letra1 = 'A';
char letra2 = 'B';
System.out.println("As letras são: "
+ letra1 + " e " + letra2);
System.exit(0);
}
}
Observe que um literal string deve estar entre aspas duplas, enquanto que um literal do tipo caractere deve estar entre aspas simples. Desta forma, "H" é uma string e 'H' é um caractere. O tipo char é integral mas sem sinal. A faixa de uma variável deste tipo vai de 0 à 65536. Os caracteres em Java são codificados em Unicode, que é um codificação de 16 bits capaz de representar uma larga faixa de caracteres internacionais. Se os 9 bits mais significantes de um char forem todos 0, então a codificação será a mesma que o ASCII de 7 bits. É possível atribuir literais inteiros à uma variável do tipo char. Veja:
public class Estudos{
public static void main(String args[]){
char letra = 98;
System.out.println("A letra é: "
+ letra);
System.exit(0);
}
}
Este código exibirá o caractere 'b'. Veja um exemplo no qual imprimimos todas as letras do alfabeto minúsculo:
public class Estudos{
public static void main(String args[]){
for(char i = 97; i <= 122; i++){
System.out.print(i + " ");
}
System.exit(0);
}
}
O tipo char pode ser convertido (sem a necessidade de cast) para os seguintes tipos: char -> int -> long -> float -> double Não é possível converter um char em um short ou byte. Caso isso seja realmente necessário, temos que fazer uma coerção (cast). Veja:
public class Estudos{
public static void main(String args[]){
char letra = 57;
byte valor = (byte)(letra);
System.exit(0);
}
}
É fácil entender porque um char não pode ser convertido implicitamente em um byte. Um char possui 16 bits enquanto um byte possui apenas 8 bits. Mas, um short possui 16 bits. Assim, o que impede a conversão implicita de um char para um short? É simples. Como o tipo short possui sinal (aceita valores negativos) e o tipo char é sem sinal, o resultado é que o tipo short possui um bit a menos (reservado para o sinal) e portanto, não pode acomodar os 16 bits do tipo char. |
Java ::: Dicas & Truques ::: Expressões Regulares |
Como remover todos os espaços de uma string em Java usando expressões regularesQuantidade de visualizações: 8217 vezes |
|
Nesta dica mostrarei como usar o método replaceAll() da classe Matcher da linguagem Java para remover todos os espaços de um texto ou frase. Esta classe faz parte do pacote java.util.regex e é usada em quase todos os códigos Java envolvendo expressões regulares. Veja o código completo para o exemplo:
package arquivodecodigos;
import java.util.regex.*;
public class Estudos{
public static void main(String args[]){
String padrao = "\\s";
Pattern regPat = Pattern.compile(padrao);
String frase = "Esta frase contém alguns espaços";
System.out.println(frase);
Matcher matcher = regPat.matcher(frase);
String res = matcher.replaceAll("");
System.out.println("Sem espaços: " + res);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Esta frase contém alguns espaços Sem espaços: Estafrasecontémalgunsespaços |
Java ::: Java para Engenharia ::: Eletricidade, Circuitos Elétricos e Eletrônicos |
Como calcular corrente, voltagem, resistência e potência em um circuito série de corrente contínua usando JavaQuantidade de visualizações: 2048 vezes |
|
Como calcular corrente, voltagem, resistência e potência em um círcuito série de corrente contínua usando Java Nesta dica mostrarei como é possível usar operações básicas da linguagem Java para calcular a corrente, voltagem, resistência e potência em um circuito série de corrente contínua. É conhecido como um circuito série um circuito composto exclusivamente por componentes elétricos ou eletrônicos conectados em série (de conexão em série, que é o mesmo que associação em série ou ligação em série). A associação em série é uma das formas básicas de se conectarem componentes elétricos ou eletrônicos. A nomeação descreve o método como os componentes são conectados. Vanos começar analisando a seguinte imagem: 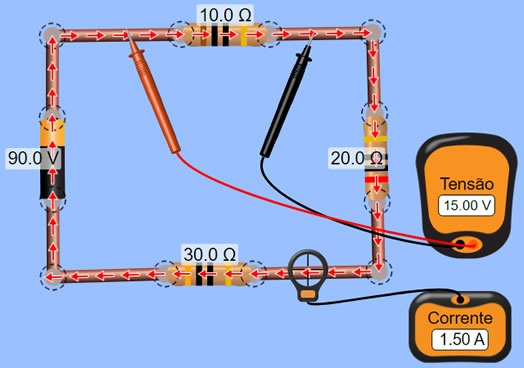 Esta imagem foi extraída do Simulador do PHET, no endereço https://phet.colorado.edu. Note que temos uma fonte de alimentação 90V, e três resistores (com resistências de 10Ω, 20Ω e 30Ω). Vamos começar relembrando os aspectos importantes dos circuitos em série: 1) A corrente elétrica I (medida em ampères (A), ou coulombs por segundo) é comum a todos os elementos do circuito. 2) A tensão elétrica V, (medida em volts (V), ou joules por coulomb) é dividida entre as cargas, ou seja, a soma das tensões nas cargas deve ser igual à tensão da fonte de alimentação. 3) A resistência elétrica R (medida em ohms (Ω)) total do circuito é igual à soma de todas as resistências das cargas. 4) A potência total P (medida em watts (W)) é igual à soma das potências das cargas que compõem o circuito. Vamos escrever um pouco de código então? Veja nosso primeiro código Java que calcula a corrente total, a tensão total, a resistência total e a potência total do circuito em série mostrado na imagem:
package estudos_java;
public class Estudos{
public static void main(String[] args){
// Tensão total do circuito em série
double eTotal = 90.0;
// Resitência total
double resist1 = 10.0;
double resist2 = 20.0;
double resist3 = 30.0;
double rTotal = resist1 + resist2 + resist3;
// Corrente elétrica total
double iTotal = eTotal / rTotal;
// Potência elétrica total
double pTotal = eTotal * iTotal;
// mostra os valores
System.out.println("Tensão total: " + eTotal);
System.out.println("Resistência total: " + rTotal);
System.out.println("Corrente total: " + iTotal);
System.out.println("Potência total: " + pTotal);
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Tensão total: 90.0 Resistência total: 60.0 Corrente total: 1.5 Potência total: 135.0 Pronto! Agora que já sabemos o valor da corrente elétrica, e sabemos que a corrente é comum a todos os elementos do circuito em série, podemos calcular a tensão individual dos componentes. Assim, veja um trecho de código Java que calcula a tensão elétrica nos três resistores (lembre-se: tensão é o produto da corrente pela resistência):
package estudos_java;
public class Estudos{
public static void main(String[] args){
// Tensão total do circuito em série
double eTotal = 90.0;
// Resitência total
double resist1 = 10.0;
double resist2 = 20.0;
double resist3 = 30.0;
double rTotal = resist1 + resist2 + resist3;
// Corrente elétrica total
double iTotal = eTotal / rTotal;
// Potência elétrica total
double pTotal = eTotal * iTotal;
// mostra os valores
System.out.println("Tensão total: " + eTotal);
System.out.println("Resistência total: " + rTotal);
System.out.println("Corrente total: " + iTotal);
System.out.println("Potência total: " + pTotal);
// mostra as tensões nos resistores
System.out.println("\nTensão nos resistores individuais:");
double e1 = resist1 * iTotal;
double e2 = resist2 * iTotal;
double e3 = resist3 * iTotal;
System.out.println("Tensão no Resistor 1: " + e1 + "V");
System.out.println("Tensão no Resistor 2: " + e2 + "V");
System.out.println("Tensão no Resistor 3: " + e3 + "V");
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Tensão total: 90.0 Resistência total: 60.0 Corrente total: 1.5 Potência total: 135.0 Tensão nos resistores individuais: Tensão no Resistor 1: 15.0V Tensão no Resistor 2: 30.0V Tensão no Resistor 3: 45.0V Para finalizar, vamos calcular a potência dissipada em cada um dos resistores de forma individual. Observe que a potência é o produto da tensão pela corrente (P = E.I). Eis o código:
package estudos_java;
public class Estudos{
public static void main(String[] args){
// Tensão total do circuito em série
double eTotal = 90.0;
// Resitência total
double resist1 = 10.0;
double resist2 = 20.0;
double resist3 = 30.0;
double rTotal = resist1 + resist2 + resist3;
// Corrente elétrica total
double iTotal = eTotal / rTotal;
// Potência elétrica total
double pTotal = eTotal * iTotal;
// mostra os valores
System.out.println("Tensão total: " + eTotal);
System.out.println("Resistência total: " + rTotal);
System.out.println("Corrente total: " + iTotal);
System.out.println("Potência total: " + pTotal);
// mostra as tensões nos resistores
System.out.println("\nTensão nos resistores individuais:");
double e1 = resist1 * iTotal;
double e2 = resist2 * iTotal;
double e3 = resist3 * iTotal;
System.out.println("Tensão no Resistor 1: " + e1 + "V");
System.out.println("Tensão no Resistor 2: " + e2 + "V");
System.out.println("Tensão no Resistor 3: " + e3 + "V");
// mostra as potências dissapadas nos resistores
System.out.println("\nPotência dissipada nos resistores individuais:");
double p1 = e1 * iTotal; // Potência = Tensão x Corrente
double p2 = e2 * iTotal;
double p3 = e3 * iTotal;
System.out.println("Potência no Resistor 1: " + p1 + "W");
System.out.println("Potência no Resistor 2: " + p2 + "W");
System.out.println("Potência no Resistor 3: " + p3 + "W");
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Tensão total: 90.0 Resistência total: 60.0 Corrente total: 1.5 Potência total: 135.0 Tensão nos resistores individuais: Tensão no Resistor 1: 15.0V Tensão no Resistor 2: 30.0V Tensão no Resistor 3: 45.0V Potência dissipada nos resistores individuais: Potência no Resistor 1: 22.5W Potência no Resistor 2: 45.0W Potência no Resistor 3: 67.5W |
VisuAlg ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em VisuAlg dados dois pontos no plano cartesianoQuantidade de visualizações: 637 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem VisuAlg que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
algoritmo "Calcular o coeficiente angular de uma reta em VisuAlg"
var
// coordenadas dos dois pontos
x1, y1, x2, y2: real
// guarda o coeficiente angular
m: real
inicio
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos calcular o coeficiente angular
m <- (y2 - y1) / (x2 - x1)
// mostramos o resultado
escreva("O coeficiente angular é: ", m)
fimalgoritmo
Ao executar este código VisuAlg nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.6666666666666666 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
algoritmo "Calcular o coeficiente angular de uma reta em VisuAlg"
var
// coordenadas dos dois pontos
x1, y1, x2, y2: real
// guarda os comprimentos dos catetos oposto e adjascente
cateto_oposto, cateto_adjascente: real
// guarda o ângulo tetha (em radianos) e a tangente
tetha, tangente: real
inicio
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos obter o comprimento do cateto oposto
cateto_oposto <- y2 - y1
// e agora o cateto adjascente
cateto_adjascente <- x2 - x1
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
tetha <- ArcTan(cateto_oposto / cateto_adjascente)
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
tangente <- Tan(tetha)
// mostramos o resultado
escreva("O coeficiente angular é: ", tangente)
fimalgoritmo
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
PHP ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como converter radianos em graus em PHP usando a função rad2deg()Quantidade de visualizações: 9858 vezes |
|
As unidades graus e radianos são muito usadas em cálculos de trigonometria, especialmente em aplicações que lidam com geometria, topografia e engenharia. O grau é de uso mais no cotidiano, pela sua praticidade, pois envolve na maioria dos casos números inteiros. O radiano, por sua vez, é de uso em cálculos envolvendo geralmente números racionais. Este trecho de código PHP mostra como converter radianos em graus usando a função rad2deg().
<?php
// vamos definir um valor em radianos
$radianos = 1.45;
// agora vamos converter para graus
$graus = rad2deg($radianos);
echo $radianos . " radianos convertido para graus é " .
$graus . "<br>";
// outra forma:
echo $radianos . " radianos convertido para graus é " .
($radianos * 180) / pi();
?>
Ao executar este código PHP nós teremos o seguinte resultado: 1.45 radianos convertido para graus é 83.078880293969 |
Java ::: Dicas & Truques ::: Imagens e Processamento de Imagens |
Como carregar uma imagem em um JFrame do Java Swing - Manipulação de imagens em JavaQuantidade de visualizações: 19563 vezes |
|
Nesta dica mostrarei como é possível combinar as classes Toolkit e MediaTracker para carregar uma imagem JPG e exibi-la na superfície da uma janela JFrame do Java Swing. Este exemplo é muito útil, pois abre o horizonte para uma infinidade de aplicações interessantes, deste visualizadores de imagens e fotos até jogos em Java. Veja o código completo para o exemplo:
import java.awt.*;
import javax.swing.*;
public class Estudos extends JFrame{
private Image imagem;
public Estudos() {
super("Carregando imagens em uma JFrame");
// imagem a ser exibida
String minhaImagem = "foto1.jpg";
Toolkit toolkit = Toolkit.getDefaultToolkit();
imagem = toolkit.getImage(minhaImagem);
MediaTracker mediaTracker = new MediaTracker(this);
mediaTracker.addImage(imagem, 0);
try{
mediaTracker.waitForID(0);
}
catch(InterruptedException ie){
System.err.println(ie);
System.exit(1);
}
setSize(imagem.getWidth(null), imagem.getHeight(null));
setVisible(true);
}
public static void main(String args[]){
Estudos app = new Estudos();
app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
public void paint(Graphics graphics){
graphics.drawImage(imagem, 0, 0, null);
}
}
Ao executar esta aplicação Java Swing nós teremos o seguinte resultado:  |
JavaScript ::: Dicas & Truques ::: Formatação de datas, strings e números |
Como exibir apenas dois dígitos após o ponto decimal em JavaScript usando a função toFixed() do objeto NumberQuantidade de visualizações: 12775 vezes |
|
Nesta dica mostrarei como podemos usar a função toFixed() do objeto Number da linguagem JavaScript para convertermos um valor de ponto flutuante em uma string (em texto). Durante a conversão nós vamos especificar que queremos apenas dois dígitos depois do ponto decimal. Veja o código JavaScript completo para o exemplo:
<!DOCTYPE html>
<head>
<meta http-equiv="Content-Type" content="text/html;
charset=iso-8859-1" />
<title>Estudos JavaScript</title>
</head>
<body>
<script type="text/javascript">
// vamos obter o valor de
// PI 3.141592653589793
var valor = Math.PI;
document.write("PI: " + valor);
// agora vamos converter o valor de PI para
// string e arredondar para o número de
// decimais desejados
var res = valor.toFixed(2);
document.write("<br>Resultado: " + res);
</script>
</body>
</html>
Ao executar este código JavaScript nós teremos o seguinte resultado: PI: 3.141592653589793 Resultado: 3.14 |
Nossas 20 dicas & truques de programação mais populares |
|
C# - Como remover um elemento em uma determinada posição de uma List<T> do C# usando a função RemoveAt() JavaScript - Como calcular o cateto oposto dadas as medidas da hipotenusa e do cateto adjascente em JavaScript Java - Programação Orientada a Objetos em Java - Como usar o modificador static em suas aplicações Java AutoCAD .NET API C# - Como selecionar uma polilinha no AutoCAD e mostrar as coordenadas de suas vértices usando a AutoCAD .NET C# API |
Você também poderá gostar das dicas e truques de programação abaixo |
|
JavaScript - Como remover o primeiro elemento de um array em JavaScript - Como usar a função shift() do objeto Array do JavaScript |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




