Java ::: Pacote java.lang ::: Integer |
Java Básico - Como usar a constante SIZE da classe Integer para obter a quantidade de bits necessária para armazenar um intQuantidade de visualizações: 6817 vezes |
Em algumas situações gostaríamos de obter a quantidade de bits necessária para armazenar um valor do tipo int (inteiro). Para isso podemos usar a constante SIZE da classe Integer (uma classe wrapper que encapsula o valor primitivo int). Veja como isso pode ser feito:
public class Estudos {
public static void main(String[] args) {
// vamos obter a quantidade de bits necessária para representar um int
int quantBits = Integer.SIZE;
// o resultado
System.out.println("Um int ocupa " + quantBits + " bits, ou seja, " +
(quantBits / 8) + " bytes");
}
}
Ao executarmos este código o resultado será: Um int ocupa 32 bits, ou seja, 4 bytes. |
jQuery ::: Dicas & Truques ::: AJAX |
Quais os parâmetros que podem ser usados com o método ajax() da biblioteca jQueryQuantidade de visualizações: 13295 vezes |
|
O método ajax() do jQuery aceita um mapa de opções para a requisição HTTP a ser realizada. Boa parte destas opções possuem valores padrões e, portanto, não precisam ser especificadas. A lista a seguir mostra os parâmetros disponíveis para o método ajax() na versão 1.2.3: url: Uma string contendo a URL para a qual a requisição HTTP será feita. type (opcional): Uma string definindo o método HTTP a ser usado na requisição (GET ou POST). O valor padrão é GET. dataType (opcional): Uma string definindo o tipo de dados aguardados como resposta do servidor (xml, html, json ou script). ifModified (opcional): Um valor Boolean indicando se o servidor deverá verificar se a página foi modificada antes de responder à requisição. timeout (opcional): O número de milisegundos após o qual a requisição sofrerá timeout e apresentará uma falha. global (opcional): Um valor Boolean indicando se gerenciadores de eventos AJAX globais serão disparados por esta requisição. O valor padrão é true. beforeSend (opcional): Uma função de callback que será executada antes da requisição HTTP ser feita. error (opcional): Uma função de callback que é executada se a requisição falhar. success (opcional): Uma função de callback que será executada se a requisição for feita com sucesso. complete (opcional): Uma função de callback que é executada quando a requisição finalizar. data (opcional): Um mapa ou string que será enviado ao servidor junto com a requisição. processData (opcional): Um valor boolean indicando se a conversão dos dados enviados em um formato objeto para o formato query-string deverá ser feita. O valor padrão é true. contentType (opcional): Uma string contendo o tipo de conteúdo MIME a ser definindo para a requisição. O valor padrão é application/x-www-form-urlencoded. async (opcional): Um valor Boolean indicando se a requisição deverá ser feita de forma assíncrona. O valor padrão é true. Nesta seção você encontra vários exemplos de uso da função ajax() do jQuery. |
VB.NET ::: Dicas & Truques ::: Matemática e Estatística |
Como resolver uma equação do segundo grau em VB.NET - Como calcular Bhaskara em VB.NETQuantidade de visualizações: 585 vezes |
|
Como resolver uma equação do 2º grau usando VB.NET Nesta dica mostrarei como encontrar as raízes de uma equação quadrática, ou seja, uma equação do 2º usando a linguagem VB.NET. Definimos como equação do 2º grau ou equações quadráticas qualquer equação do tipo ax² + bx + c = 0 em que a, b e c são números reais e a ≠ 0. Ela recebe esse nome porque, no primeiro membro da igualdade, há um polinômio de grau dois com uma única incógnita. Note que, dos coeficientes a, b e c, somente o a é diferente de zero, pois, caso ele fosse igual a zero, o termo ax² seria igual a zero, logo a equação se tornaria uma equação do primeiro grau: bx + c = 0. Independentemente da ordem da equação, o coeficiente a sempre acompanha o termo x², o coeficiente b sempre acompanha o termo x, e o coeficiente c é sempre o termo independente. Como resolver uma equação do 2º grau Conhecemos como soluções ou raízes da equação ax² + bx + c = 0 os valores de x que fazem com que essa equação seja verdadeira. Uma equação do 2º grau pode ter no máximo dois números reais que sejam raízes dela. Para resolver equações do 2º grau completas, existem dois métodos mais comuns: a) Fórmula de Bhaskara; b) Soma e produto. O primeiro método é bastante mecânico, o que faz com que muitos o prefiram. Já para utilizar o segundo, é necessário o conhecimento de múltiplos e divisores. Além disso, quando as soluções da equação são números quebrados, soma e produto não é uma alternativa boa. Como resolver uma equação do 2º grau usando Bhaskara Como nosso código VB.NET vai resolver a equação quadrática usando a Fórmula de Bhaskara, o primeiro passo é encontrar o determinante. Veja: \[\Delta =b^2-4ac\] Nem sempre a equação possui solução real. O valor do determinante é que nos indica isso, existindo três possibilidades: a) Se determinante > 0, então a equação possui duas soluções reais. b) Se determinante = 0, então a equação possui uma única solução real. c) Se determinante < 0, então a equação não possui solução real. Encontrado o determinante, só precisamos substituir os valores, incluindo o determinante, na Fórmula de Bhaskara: \[x = \dfrac{- b\pm\sqrt{b^2- 4ac}}{2a}\] Vamos agora ao código VB.NET. Nossa aplicação vai pedir para o usuário informar os valores dos três coeficientes a, b e c e, em seguida, vai apresentar as raizes da equação:
Imports System
Module Program
Sub Main(args As String())
' os coeficientes
Dim a, b, c As Double
' as duas raizes, a imaginaria e o discriminante
Dim raiz1, raiz2, imaginaria, discriminante As Double
' vamos pedir para o usuário informar os valores dos coeficientes
Console.Write("Valor do coeficiente a: ")
a = Double.Parse(Console.ReadLine())
Console.Write("Valor do coeficiente b: ")
b = Double.Parse(Console.ReadLine())
Console.Write("Valor do coeficiente c: ")
c = Double.Parse(Console.ReadLine())
' vamos calcular o discriminante
discriminante = (b * b) - (4 * a * c)
' a equação possui duas soluções reais?
If discriminante > 0 Then
raiz1 = (-b + Math.Sqrt(discriminante)) / (2 * a)
raiz2 = (-b - Math.Sqrt(discriminante)) / (2 * a)
Console.Write("Existem duas raizes: x1 = " & raiz1 _
& " e x2 = " & raiz2)
ElseIf discriminante = 0 Then
' a equação possui uma única solução real?
raiz1 = raiz2 = -b / (2 * a)
Console.Write("Existem duas raizes iguais: x1 = " _
& raiz1 & " e x2 = " & raiz2)
ElseIf discriminante < 0 Then
' a equação não possui solução real?
raiz1 = raiz2 = -b / (2 * a)
imaginaria = Math.Sqrt(-discriminante) / (2 * a)
Console.Write("Existem duas raízes complexas: x1 = " &
raiz1 & " + " & imaginaria & " e x2 = " & raiz2 _
& " - " & imaginaria)
End If
Console.WriteLine(vbCrLf & "Pressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código VB.NET nós teremos o seguinte resultado: Valor do coeficiente a: 1 Valor do coeficiente b: 2 Valor do coeficiente c: -3 Existem duas raizes: x1 = 1 e x2 = -3 |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de Java - Criando dois vetores de inteiros de forma que a soma dos elementos individuais de cada vetor seja igual a 30Quantidade de visualizações: 11616 vezes |
|
Pergunta/Tarefa: Considere os seguintes vetores:
// dois vetores de 5 inteiros cada
int a[] = {50, -2, 9, 5, 17};
int b[] = new int[5];
Sua saída deverá ser parecida com: Valores no vetor a: 50 -2 9 5 17 Valores no vetor b: -20 32 21 25 13 Veja a resolução comentada deste exercício usando Java:
package estudos;
public class Estudos {
public static void main(String[] args) {
// dois vetores de 5 inteiros cada
int a[] = {50, -2, 9, 5, 17};
int b[] = new int[5];
// vamos preencher o segundo vetor de forma que a soma dos
// valores de seus elementos seja 30
for(int i = 0; i < b.length; i++){
b[i] = 30 - a[i];
}
// vamos mostrar o resultado
System.out.print("Valores no vetor a: ");
for(int i = 0; i < a.length; i++){
System.out.print(a[i] + " ");
}
System.out.print("\nValores no vetor b: ");
for(int i = 0; i < b.length; i++){
System.out.print(b[i] + " ");
}
System.out.println();
}
}
|
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Física - Mecânica - Movimento Retilíneo Uniforme (MRU) |
Exercícios Resolvidos de Física usando Java - Dois automóveis, A e B, movem-se em movimento uniforme e no mesmo sentido. Suas velocidades escalares têm módulos respectivamente iguais a...Quantidade de visualizações: 2498 vezes |
|
Pergunta/Tarefa: Dois automóveis, A e B, movem-se em movimento uniforme e no mesmo sentido. Suas velocidades escalares têm módulos respectivamente iguais a 15 m/s e 10 m/s. No instante t = 0, os automóveis encontram-se nas posições indicadas abaixo:  Determine: a) o instante em que A alcança B; b) a que distância da posição inicial de A ocorre o encontro. Resposta/Solução: Este é um dos exemplos clássicos que encontramos nos livros de Física Mecânica, nos capítulos dedicados ao Movimento Retilíneo Uniforme (MRU). Em geral, tais exemplos são vistos como parte dos estudos de encontro e ultrapassagem de partículas. Por se tratar de Movimento Retilíneo Uniforme (MRU), as grandezas envolvidas nesse problema são: posição (deslocamento), velocidade e tempo. Assim, já sabemos de antemão que o veículo B está 100 metros à frente do veículo A. Podemos então começar calculando a posição atual na qual cada um dos veículos se encontra. Isso é feito por meio da Função Horária da Posição ou Deslocamento em Movimento Retilíneo Uniforme - MRU. Veja o código Java que nos retorna a posição inicial (em metros) dos dois veículos:
package arquivodecodigos;
public class Estudos{
public static void main(String args[]){
// valocidade do veículo A
double vA = 15; // em metros por segundo
// valocidade do veículo B
double vB = 10; // em metros por segundo
// posição inicial dos dois veículos
double sInicialA = 0;
double sInicialB = 100;
// tempo inicial em segundos
double tempo_inicial = 0;
// calcula a posição atual dos dois veículos
double sA = sInicialA + (vA * tempo_inicial);
double sB = sInicialB + (vB * tempo_inicial);
// mostra os resultados
System.out.println("A posição do veículo A é: " + sA + " metros");
System.out.println("A posição do veículo B é: " + sB + " metros");
}
}
Ao executar esta primeira parte do código Java nós teremos o seguinte resultado: A posição do veículo A é: 0.0 metros A posição do veículo B é: 100.0 metros Agora que já temos o código que calcula a posição de cada veículo, já podemos calcular o tempo no qual o veículo A alcança o veículo B. Para isso vamos pensar direito. Se o veículo A vai alcançar o veículo B, então já sabemos que a velocidade do veículo A é maior que a velocidade do veículo B. Sabemos também que a posição do veículo B é maior que a posição do veículo A. Só temos que aplicar a fórmula do tempo, que é a variação da posição dividida pela variação da velocidade. Veja o código Java que efetua este cálculo:
package arquivodecodigos;
public class Estudos{
public static void main(String args[]){
// valocidade do veículo A
double vA = 15; // em metros por segundo
// valocidade do veículo B
double vB = 10; // em metros por segundo
// posição inicial dos dois veículos
double sInicialA = 0;
double sInicialB = 100;
// tempo inicial em segundos
double tempo_inicial = 0;
// calcula a posição atual dos dois veículos
double sA = sInicialA + (vA * tempo_inicial);
double sB = sInicialB + (vB * tempo_inicial);
// calculamos o tempo no qual o veículo A alcança o veículo B
double tempo = (sB - sA) / (vA - vB);
// mostra os resultados
System.out.println("A posição do veículo A é: " + sA + " metros");
System.out.println("A posição do veículo B é: " + sB + " metros");
System.out.println("O veículo A alcança o veículo B em " + tempo +
" segundos");
}
}
Ao executar esta modificação do código Java nós teremos o seguinte resultado: A posição do veículo A é: 0.0 metros A posição do veículo B é: 100.0 metros O veículo A alcança o veículo B em 20.0 segundos O item b pede para indicarmos a que distância da posição inicial de A ocorre o encontro entre os dois veículos. Agora que já sabemos o tempo do encontro, fica muito fácil. Basta multiplicarmos a velocidade do veículo A pelo tempo do encontro. Veja:
package arquivodecodigos;
public class Estudos{
public static void main(String args[]){
// valocidade do veículo A
double vA = 15; // em metros por segundo
// valocidade do veículo B
double vB = 10; // em metros por segundo
// posição inicial dos dois veículos
double sInicialA = 0;
double sInicialB = 100;
// tempo inicial em segundos
double tempo_inicial = 0;
// calcula a posição atual dos dois veículos
double sA = sInicialA + (vA * tempo_inicial);
double sB = sInicialB + (vB * tempo_inicial);
// calculamos o tempo no qual o veículo A alcança o veículo B
double tempo = (sB - sA) / (vA - vB);
// a que distância da posição inicial de A ocorre o encontro
double distancia_encontro = vA * tempo;
// mostra os resultados
System.out.println("A posição do veículo A é: " + sA + " metros");
System.out.println("A posição do veículo B é: " + sB + " metros");
System.out.println("O veículo A alcança o veículo B em " + tempo +
" segundos");
System.out.println("O encontro ocorreu a " + distancia_encontro +
" metros da distância inicial do veículo A");
}
}
Agora o código Java completo nos mostra o seguinte resultado: A posição do veículo A é: 0.0 metros A posição do veículo B é: 100.0 metros O veículo A alcança o veículo B em 20.0 segundos O encontro ocorreu a 300.0 metros da distância inicial do veículo A Para demonstrar a importância de se saber calcular a Função Horária da Posição ou Deslocamento em Movimento Retilíneo Uniforme (MRU), experimente indicar que o veículo A saiu da posição 20 metros, e defina a posição inicial do veículo B para 120 metros, de modo que ainda conservem a distância de 100 metros entre eles. Você verá que o tempo do encontro e a distância do encontro em relação à posição inicial do veículo A continuam os mesmos. Agora experimente mais alterações nas posições iniciais, na distância e também nas velocidades dos dois veículos para entender melhor os conceitos que envolvem o Movimento Retilíneo Uniforme (MRU). |
C# ::: Windows Forms ::: Formulários e Janelas |
Como maximizar um formulário Windows Forms ao clicar em um botão usando a linguagem C#Quantidade de visualizações: 13407 vezes |
|
Em algumas situações gostaríamos de maximizar um formulário Windows Forms baseado em alguma ação do usuário. Isso pode ser feito definindo-se a constante FormWindowState.Maximized para a propriedade WindowState da classe Form. O trecho de código abaixo mostra como maximizar o formulário ao clicarmos em um botão:
private void button1_Click(object sender, EventArgs e){
// vamos maximizar o formulário
this.WindowState = FormWindowState.Maximized;
}
|
CSS ::: Dicas & Truques ::: Cores de Fundo e Imagens de Fundo |
Apostila CSS - Como definir a cor de fundo de um elemento HTML usando um valor rgbQuantidade de visualizações: 7415 vezes |
|
A propriedade background-color aceita um valor de cor que pode ser informado por meio da função rgb(). Esta função aceita valores de 0 até 255 para a cores vermelho, verde e azul, ou seja Red, Green e Blue. Veja a figura abaixo:  A cor de fundo para esta página for gerada com o seguinte código: <html> <head> <title>Estudando CSS</title> <meta name="viewport" content="width=device-width, initial-scale=1"> </head> <body style="background-color: rgb(201, 20, 58)"> </body> </html> |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Matemática e Estatística |
Exercício Resolvido de Java - Como simplificar frações em JavaQuantidade de visualizações: 754 vezes |
|
Pergunta/Tarefa: Simplificar uma fração consiste em reduzir o numerador e o denominador por meio da divisão pelo máximo divisor comum aos dois números. Uma fração está totalmente simplificada quando verificamos que seus termos estão totalmente reduzidos a números que não possuem termos divisíveis entre si. Uma fração simplificada sofre alteração do numerador e do denominador, mas seu valor matemático não é alterado, pois a fração, quando tem seus termos reduzidos, torna-se uma fração equivalente. Escreva um programa Java que pede para o usuário informar o numerador e o denominador de uma fração e mostre a fração simplificada. Use uma classe Fracao para a operação de simplificação. Em outras seções do nosso site você encontra o cálculo do MDC para encontrar o Máximo Divisor Comum. Sua saída deverá ser parecida com: Informe o numerador: 32 Informe o denominador: 40 A fração gerada foi: 32/40 A fração simplificada é: 4/5 Veja a resolução comentada deste exercício em Java:
package estudos;
import java.util.Scanner;
public class Estudos{
public static void main(String[] args) {
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// vamos pedir para o usuário informar o numerador
System.out.print("Informe o numerador: ");
int numerador = Integer.parseInt(entrada.nextLine());
// vamos pedir para o usuário informar o denominador
System.out.print("Informe o denominador: ");
int denominador = Integer.parseInt(entrada.nextLine());
// vamos criar um objeto da classe Fracao
Fracao f = new Fracao(numerador, denominador);
// vamos mostrar a fração gerada
System.out.println("A fração gerada foi: " + f.toString());
// agora vamos simplificar esta fração
System.out.println("A fração simplificada é: " +
f.simplificar().toString());
}
}
// classe usada para representar uma Fração
class Fracao{
int numerador;
int denominador;
// construtor da classe
public Fracao(int numerador, int denominador) {
this.numerador = numerador;
this.denominador = denominador;
}
// método que simplifica a fração atual e retorna o
// resultado como uma fração
public Fracao simplificar(){
// cria uma fração temporária
Fracao temp = new Fracao(this.numerador, this.denominador);
// descobrimos que é maior, o numerador ou o
// denominador
int n = temp.numerador, d = temp.denominador, maior;
// o numerador é menor que 0?
if (temp.numerador < 0) {
n = -temp.numerador;
}
// descobrimos o maior
if (n > d) {
maior = n;
}
else {
maior = d;
}
// encontramos o maior número que divide o numerador e o
// denominador
int mdc = 0;
for (int i = maior; i >= 2; i--) {
if ((temp.numerador % i == 0) && (temp.denominador % i == 0)) {
mdc = i;
break;
}
}
// agora dividimos tanto o numerador quanto o denominador
// pelo mdc encontrado
if (mdc != 0) {
temp.numerador = temp.numerador / mdc;
temp.denominador = temp.denominador / mdc;
}
// retorna a fração temporária
return temp;
}
// retorna uma representação textual dessa fração
@Override
public String toString() {
return this.numerador + "/" + this.denominador;
}
}
|
VB.NET ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em VB.NET usando a função Cos() da classe Math - Calculadora de cosseno em VB.NETQuantidade de visualizações: 1239 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função Cos() da linguagem VB.NET. Esta função, que é um método da classe Math, recebe um valor numérico Double e retorna um valor Double, ou seja, também numérico) entre -1 até 1 (ambos inclusos). Veja:
Imports System
Module Program
Sub Main(args As String())
' vamos calcular o cosseno de três números
Console.WriteLine("Cosseno de 0 = " & Math.Cos(0))
Console.WriteLine("Cosseno de 1 = " & Math.Cos(1))
Console.WriteLine("Cosseno de 2 = " & Math.Cos(2))
Console.WriteLine("\nPressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código VB.NET nós teremos o seguinte resultado: Cosseno de 0 = 1 Cosseno de 1 = 0,5403023058681397 Cosseno de 2 = -0,4161468365471424 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 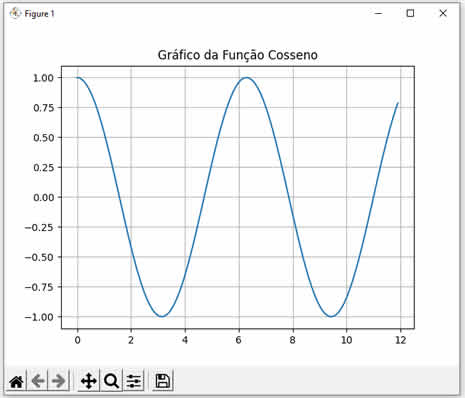 |
C ::: C para Engenharia ::: Física - Mecânica |
Como calcular a velocidade da queda livre de um corpo dado o intervalo de tempo (e a aceleração da gravidade) em CQuantidade de visualizações: 2563 vezes |
|
A Queda Livre é um Movimento Uniformemente Variado, na qual um objeto em queda livre tem a sua velocidade aumentada a taxas constantes. Abandonado em alturas próximas da terra, a velocidade com que um corpo cai aumenta a uma taxa de aproximadamente 9,8m/s. Isso é o mesmo que dizer que a aceleração da gravidade terrestre é de 9,8m/s2, o que aumenta a velocidade do objeto em 35,28km/h a cada segundo. Assim, a fórmula da velocidade de um objeto em queda livre é: \[ \text{v} = \text{g} \cdot \text{t} \] Onde: v ? velocidade de queda (m/s) g ? aceleração da gravidade (m/s2) t ? intervalo de tempo (s) Vamos ver um exemplo? Veja o seguinte enunciado: 1) Um corpo é abandonado a uma altura qualquer no tempo 0s e está em queda livre. Calcule a sua velocidade no tempo 15s. Como sabemos que o intervalo de tempo é 15s, só precisamos jogar na fórmula. Veja o código C completo para o cálculo:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
// gravidade terrestre em m/s2
float gravidade = 9.80665;
// intervalo de tempo da queda livre (em segundos)
float tempo = 15.00; // em segundos
// velocidade da queda nesse intervalo
float velocidade = gravidade * tempo;
// mostramos o resultado
printf("A velocidade da queda livre é: %fm/s",
velocidade);
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: A velocidade da queda livre é: 147.099747m/s Se quisermos saber a velocidade em km/h, basta multiplicar o resultado por 3.6, o que dará 529.56km/h. Vamos tornar o experimento mais interessante? Veja uma modificação no código C que mostra a velocidade da queda nos 10 primeiros segundos, de forma individual:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
int i; // variável de controle do laço
// gravidade terrestre em m/s2
float gravidade = 9.80665;
// intervalo de tempo da queda livre (em segundos)
int tempo;
// velocidade da queda nesse intervalo
float velocidade;
// um laço for que repete 10 vezes
for(i = 1; i <= 10; i++){
tempo = i; // inicialmente será um segundo
velocidade = gravidade * tempo;
printf("A velocidade no tempo %d: %fm/s\n",
tempo, velocidade);
}
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: A velocidade no tempo 1: 9.806650m/s A velocidade no tempo 2: 19.613300m/s A velocidade no tempo 3: 29.419950m/s A velocidade no tempo 4: 39.226601m/s A velocidade no tempo 5: 49.033249m/s A velocidade no tempo 6: 58.839901m/s A velocidade no tempo 7: 68.646553m/s A velocidade no tempo 8: 78.453201m/s A velocidade no tempo 9: 88.259850m/s A velocidade no tempo 10: 98.066498m/s |
Nossas 20 dicas & truques de programação mais populares |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Java - Java Swing para iniciantes - Como detectar eventos do teclado em uma janela JFrame do Java Swing JavaScript - Cookies em JavaScript - Como escrever uma função para a criação de cookies em JavaScript JavaScript - Como calcular a equação reduzida da reta em JavaScript dados dois pontos pertencentes à reta |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






