C# ::: Dicas & Truques ::: Arquivos e Diretórios |
Como testar se um diretório existe em C# usando a propriedade Exists da classe DirectoryInfoQuantidade de visualizações: 1 vezes |
|
Em algumas situações nós precisamos verificar se um diretório existe em C#, talvez para ler ou gravar dados neste arquivo. Isso pode ser feito por meio da propriedade Exists da classe DirectoryInfo. Esta propriedade retorna um valor true se o diretório existir e false em caso contrário. Veja o código completo para o exemplo:
using System;
using System.IO;
namespace Estudos {
class Principal {
static void Main(string[] args) {
// vamos criar uma nova instância da classe DirectoryInfo
DirectoryInfo dir = new DirectoryInfo(@"C:\estudos_csharp\imagens");
// vamos testar se o diretório existe
if (dir.Exists) {
Console.Write("Diretório existe");
}
else {
Console.Write("Diretório não existe");
}
Console.WriteLine("\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: O diretório existe. |
C ::: Dicas & Truques ::: Matemática e Estatística |
Como testar se um número é primo em CQuantidade de visualizações: 2628 vezes |
|
O Número Primo é o número maior que 1 e que só pode ser dividido por 1 e por ele mesmo, ou seja, números primos não podem ser divididos por outros números, a não ser por ele mesmo e pelo número 1. Dessa forma, 2, 3, 5, 7, 11, 13, 17, etc, são todos números primos. É importante observar que 0 e 1 não são números primos, e que o número 2 é o único número primo par. Veja agora um código C completo que pede para o usuário informar um número inteiro positivo e mostra uma mensagem indicando se o número informado é primo ou não:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
int numero, i;
int primo = 1; // verdadeiro, true
// vamos solicitar um número inteiro positivo
printf("Informe um número inteiro positivo: ");
scanf("%d", &numero);
// o número é negativo?
if(numero < 0){
printf("Número inválido.\n\n");
}
// é 0 ou 1?
else if((numero == 0) || (numero == 1)){
printf("Número válido, mas não é primo.\n\n");
}
// passou até aqui. Vamos testar se o número é primo
else{
for (i = 2; i <= (numero / 2); i++){
// se passar no teste, não é primo
if (numero % i == 0) {
primo = 0; // recebe false
break;
}
}
if(primo){
printf("O número informado é primo\n\n");
}
else{
printf("O número informado não é primo\n\n");
}
}
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: Informe um número inteiro positivo: 9 O número informado não é primo |
Python ::: Pandas Python Library (Biblioteca Python Pandas) ::: DataFrame |
Como retornar a quantidade de linhas em um DataFrame do Pandas usando a função len() e a propriedade indexQuantidade de visualizações: 2035 vezes |
|
Podemos tirar proveito da função len() do Python e da propriedade index do DataFrame do Pandas para contarmos as linhas do DataFrame. Lembre-se de que a propriedade index representa os rótulos das linhas. Veja o código completo para o exemplo:
# importamos a biblioteca Pandas
import pandas as pd
def main():
# vamos carregar os dados do arquivo .csv
df = pd.read_csv("C:\\estudos_python\\carros.csv",
delimiter=";")
# vamos mostrar o DataFrame resultante
print("Os dados do DataFrame são:\n")
print(df)
# agora vamos retornar a quantidade de linhas no DataFrame
quant_linhas = len(df.index)
# e mostramos o resultado
print("\nO DataFrame contém {0} linhas".format(quant_linhas))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado:
Os dados do DataFrame são:
Marca Modelo Ano Valor Vendido
0 Fiat Sienna 2010.0 23500.0 S
1 Volkswagen Polo NaN 31453.0 N
2 Volkswagen NaN 2001.0 19200.0 S
3 Fiat Palio 1995.0 7500.0 S
4 Honda Civic NaN 42000.0 S
5 Renault Sandero 2010.0 52000.0 N
6 Ford Focus 2009.0 42700.0 N
O DataFrame contém 7 linhas
|
Python ::: NumPy Python Library (Biblioteca Python NumPy) ::: Arrays e Matrix (Vetores e Matrizes) |
Como repetir os elementos de um vetor ou matriz usando a função repeat() da NumPy do PythonQuantidade de visualizações: 878 vezes |
|
A função repeat() da biblioteca NumPy do Python é usada quando queremos repetir os elementos de um vetor ou matriz um determinado número de vezes. Em sua forma mais simples esta função pede um array e um número inteiro indicando a quantidade de repetições. Veja o código Python completo para o exemplo:
# vamos importar a biblioteca NumPy
import numpy as np
def main():
# vamos criar um vetor contendo 5 elementos
vetor = np.array([5, 3, 9, 1, 4])
# agora vamos aplicar a função repeat() a este vetor
novo_vetor = np.repeat(vetor, 3)
# vamos mostrar o resultado
print("O vetor original é: {0}".format(vetor))
print("O novo vetor é: {0}".format(novo_vetor))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: O vetor original é: [5 3 9 1 4] O novo vetor é: [5 5 5 3 3 3 9 9 9 1 1 1 4 4 4] Veja agora o efeito desta função em uma matriz de 2 linhas por 3 colunas:
# vamos importar a biblioteca NumPy
import numpy as np
def main():
# vamos criar uma matriz de 2 linhas e 3 colunas
matriz = np.array([(1, 2, 3), (4, 5, 6)])
# agora vamos aplicar a função repeat() a esta matriz
nova_matriz = np.repeat(matriz, 3, 0)
# vamos mostrar o resultado
print("A matriz original é:\n\n{0}".format(matriz))
print("A nova matriz é:\n\n{0}".format(nova_matriz))
if __name__== "__main__":
main()
Note que informei o valor 0 para o terceiro parâmetro da função repeat(). Isso faz com que os elementos da matriz sejam repetidos no eixo x. Veja: A matriz original é: [[1 2 3] [4 5 6]] A nova matriz é: [[1 2 3] [1 2 3] [1 2 3] [4 5 6] [4 5 6] [4 5 6]] Se trocarmos o valor 0 por 1, o resultado será: A matriz original é: [[1 2 3] [4 5 6]] A nova matriz é: [[1 1 1 2 2 2 3 3 3] [4 4 4 5 5 5 6 6 6]] |
Delphi ::: Dicas & Truques ::: Matemática e Estatística |
Como calcular desvio padrão em Delphi - Delphi para Matemática e EstatísticaQuantidade de visualizações: 2148 vezes |
|
Em Matemática e Estatística, o Desvio padrão (em inglês: Standard Deviation) é uma medida de dispersão, ou seja, é uma medida que indica o quanto um conjunto de dados é uniforme. Quando o desvio padrão é baixo, isso quer dizer que os dados do conjunto estão mais próximos da média. Como calcular o desvio padrão de um conjunto de dados? Vamos começar analisando a fórmula mais difundida na matemática e na estatística: \[\sigma = \sqrt{ \frac{\sum_{i=1}^N (x_i -\mu)^2}{N}}\] Onde: a) __$\sigma__$ é o desvio; b) __$x_i__$ é um valor qualquer no conjunto de dados na posição i; c) __$\mu__$ é a média aritmética dos valores do conjunto de dados; d) N é a quantidade de valores no conjunto. O somatório dentro da raiz quadrada nos diz que devemos somar todos os elementos do conjunto, desde a posição 1 até a posição n, subtrair cada valor pela média do conjunto e elevar ao quadrado. Obtida a soma, nós a dividimos pelo tamanho do conjunto. Veja o código Delphi completo que obtém o desvio padrão a partir de um conjunto de dados contendo quatro valores:
// Algoritmo Delphi para calcular desvio padrão
program estudos_delphi;
{$APPTYPE CONSOLE}
uses
SysUtils, Math;
var
// conjunto de dados
conjunto: array[1..4] of double = (10, 30, 90, 30);
soma: double; // Soma dos elementos
desvio_padrao: double; // Desvio padrão
tam: integer; // Tamanho dos dados
media: double; // média
i: integer;
begin
soma := 0.0;
desvio_padrao := 0.0;
tam := 4;
// vamos somar todos os elementos
for i := 1 to tam do
begin
soma := soma + conjunto[i];
end;
// agora obtemos a média do conjunto de dados
media := soma / tam;
// e finalmente obtemos o desvio padrão
for i := 1 to tam do
begin
// não esqueça de adicionar a unit Math
desvio_padrao := desvio_padrao + Power(conjunto[i] - media, 2);
end;
// mostramos o resultado
WriteLn('Desvio Padrão Populacional: ' + FloatToStr(Sqrt(desvio_padrao / tam)));
WriteLn('Desvio Padrão Amostral: ' + FloatToStr(Sqrt(desvio_padrao / (tam - 1))));
WriteLn;
Write('Pressione Enter para sair...');
ReadLn;
end.
Ao executar este código Delphi nós teremos o seguinte resultado: Desvio Padrão Populacional: 30.0 Desvio Padrão Amostral: 34.64101615137755 Veja que, para calcular o Desvio Padrão Populacional, nós dividimos o somatório pela quantidade de elementos no conjunto, enquanto, para calcular o Desvio Padrão Amostral, nós dividimos o somatório pela quantidade de elementos - 1 (cuidado com a divisão por zero no caso de um conjunto com apenas um elemento). |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Geometria, Trigonometria e Figuras Geométricas |
Exercícios Resolvidos de Java - Como calcular a área de um losango em JavaQuantidade de visualizações: 4926 vezes |
|
Pergunta/Tarefa: Um losango é um quadrilátero equilátero, ou seja, é um polígono formado por quatro lados de igual comprimento. Um losango é também um paralelogramo. Alguns autores exigem ainda que nenhum dos ângulos do quadrilátero seja reto para que ele seja considerado um losango. A área (em metros quadrados) de um losango pode ser calculada usando-se a seguinte fórmula: 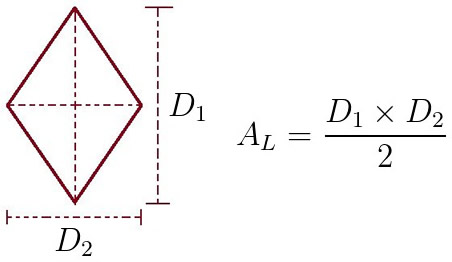 Onde D1 é a diagonal maior e D2 é a diagonal menor. Escreva um programa Java que leia a diagonal maior e a diagonal menor e calcule a área do losango. Sua saída deverá ser parecida com: Informe a medida da diagonal maior: 5 Informe a medida da diagonal menor: 10 A área (em metros quadrados) do losango é: 25 Veja a resolução comentada deste exercício usando Java console:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
Scanner entrada = new Scanner(System.in);
// vamos ler os valores das diagonais maior e menor
System.out.print("Informe a medida da diagonal maior: ");
int diagonalMaior = Integer.parseInt(entrada.nextLine());
System.out.print("Informe a medida da diagonal menor: ");
int diagonalMenor = Integer.parseInt(entrada.nextLine());
// calcula a area do losango
int area = (diagonalMaior * diagonalMenor) / 2;
// mostra o resultado
System.out.println("A área (em metros quadrados) do losango é: " + area);
System.out.println("\n");
}
}
|
Java ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Tutorial de Java - Como usar a instrução condicional if e if...else do JavaQuantidade de visualizações: 54074 vezes |
Instruções if e if...else permitem executar trechos de códigos baseado em condições. Veja um exemplo:
public class Estudos{
public static void main(String args[]){
int valor = 5;
if(valor > 3)
System.out.println("Valor maior que 3");
}
}
Neste programa, a instrução
System.out.println("Valor maior que 3");
será executada somente se o teste (valor > 3) for verdadeiro. Observe que a expressão de teste deverá sempre ser do tipo boolean (true ou false). Neste exemplo temos apenas uma instrução a ser executada. Isso dispensa o uso das chaves ao redor do bloco de códigos. Se o bloco contiver mais de uma instrução, as chaves são necessárias. Veja:
public class Estudos{
public static void main(String args[]){
int valor = 5;
if(valor > 3){
System.out.println("Valor maior que 3");
System.out.println("O valor é: " + valor);
}
}
}
A instrução if...else (se...senão) é usada quando queremos fornecer um caminho alternativo ao código. Veja:
public class Estudos{
public static void main(String args[]){
int valor = 1;
if(valor > 3)
System.out.println("Valor maior que 3");
else
System.out.println("Valor menor que 3");
}
}
Você pode ainda usar if...else if...else (se...senão se...senão). Veja:
public class Estudos{
public static void main(String args[]){
int valor = 3;
if(valor > 3)
System.out.println("Valor maior que 3");
else if(valor < 3)
System.out.println("Valor menor que 3");
else
System.out.println("Valor é igual a 3");
}
}
|
C ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cateto oposto dadas as medidas da hipotenusa e do cateto adjascente em CQuantidade de visualizações: 3118 vezes |
|
Todos estamos acostumados com o Teorema de Pitágoras, que diz que "o quadrado da hipotenusa é igual à soma dos quadrados dos catetos". Baseado nessa informação, fica fácil retornar a medida do cateto oposto quando temos as medidas da hipotenusa e do cateto adjascente. Isso, claro, via programação em linguagem C. Comece observando a imagem a seguir:  Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. A medida da hipotenusa é, sem arredondamentos, 36.056 metros. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras): \[c^2 = a^2 + b^2\] Tudo que temos que fazer é mudar a fórmula para: \[a^2 = c^2 - b^2\] Veja que agora o quadrado do cateto oposto é igual ao quadrado da hipotenusa menos o quadrado do cateto adjascente. Não se esqueça de que a hipotenusa é o maior lado do triângulo retângulo. Veja agora como esse cálculo é feito em linguagem C:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(int argc, char *argv[]){
float c = 36.056; // medida da hipotenusa
float b = 30; // medida do cateto adjascente
// agora vamos calcular o comprimento da cateto oposto
float a = sqrt(pow(c, 2) - pow(b, 2));
// e mostramos o resultado
printf("A medida do cateto oposto é: %f", a);
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: A medida do cateto oposto é: 20.000877 Como podemos ver, o resultado retornado com o código C confere com os valores da imagem apresentada. |
Python ::: wxPython ::: Controles Visuais Básicos do wxPython |
Como obter o texto de um botão wx.Button do wxPython e exibí-lo em uma mensagem wx.MessageDialog usando a função GetLabel()Quantidade de visualizações: 6836 vezes |
|
Como obter o texto de um botão wx.Button do wxPython e exibí-lo em uma mensagem wx.MessageDialog usando a função GetLabel() O texto (rótulo) de um wx.Button do framework wxPython pode ser obtido com uma chamada à função GetLabel(). O exemplo abaixo mostra uma aplicação completa e detalha como clicar em um botão, obter seu texto e exibí-lo em uma caixa de mensagem:
# vamos importar a biblioteca wxPython
import wx
class Janela(wx.Frame):
def __init__(self):
wx.Frame.__init__(self, None, -1,
"Usando wx.Button", size=(350, 200))
# Cria um painel
panel = wx.Panel(self)
# Cria um botão e o adiciona no painel
self.btn = wx.Button(panel, label="Clique Aqui",
pos=(10, 10), size=(100, 25))
# Anexa um evento ao botão
self.Bind(wx.EVT_BUTTON, self.OnBtnClick, self.btn)
# Método que será chamado ao clicar o botão
def OnBtnClick(self, event):
texto_btn = self.btn.GetLabel()
dlg = wx.MessageDialog(None, u"O texto do botão é: "
+ texto_btn, "Usando wx.Button", wx.OK | wx.ICON_INFORMATION)
result = dlg.ShowModal()
dlg.Destroy()
if __name__ == "__main__":
app = wx.App()
janela = Janela()
janela.Show(True)
app.MainLoop()
|
PHP ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como converter graus em radianos em PHP usando a função deg2rad() - Trigonometria para iniciantesQuantidade de visualizações: 14395 vezes |
|
As unidades grau e radiano são muito usadas em cálculos de trigonometria. O grau é de uso mais no cotidiano pela sua praticidade, pois envolve, na maioria dos casos, números inteiros. O radiano é de uso em cálculos envolvendo geralmente números racionais (e também na programação gráfica, uma vez que praticamente todas as linguagens de programação possuem funções de trigonometria que requerem e retornam valores em radianos, e não em graus). Graus podem ser convertidos para radianos usando-se a seguinte fórmula:  Note que o valor de PI é 3,14 (aproximadamente). Veja agora um trecho de código PHP que converte um ângulo em graus para radianos: <html> <head> <title>Estudando PHP</title> </head> <body> <?php $graus = 45; $radianos = ($graus / 180) * pi(); echo "Ângulo em graus: " . $graus . "<br>"; echo "Ângulo em radianos: " . $radianos; ?> </body> </html> Ao executarmos este código nós teremos o seguinte resultado: Ângulo em graus: 45 Ângulo em radianos: 0.78539816339745 O PHP, na contramão de várias outras linguagens de programação, nos fornece uma função já embutida que nos permite converter de graus para radianos. Esta função se chama deg2rad(), recebe um valor em graus e devolve o resultado em radianos. Veja como usá-la no código PHP abaixo: <html> <head> <title>Estudando PHP</title> </head> <body> <?php $graus = 45; $radianos = deg2rad($graus); echo "Ângulo em graus: " . $graus . "<br>"; echo "Ângulo em radianos: " . $radianos; ?> </body> </html> Ao executarmos o código novamente, teremos o seguinte resultado: Ângulo em graus: 45 Ângulo em radianos: 0.78539816339745 Veja que o resultado obtido com o uso da função deg2rad() foi o mesmo que obtivemos com o cálculo no início da dica. Para finalizar, saiba que 45o, assim como 30o e 60o são conhecidos como ângulos notáveis, e seus valores em radianos, assim como seus seno, cosseno e tangentes, devem ser memorizados se você quiser se tornar um guru (ou guroa) em geometria e trigonometria (e em computação gráfica, é claro). |
Nossas 20 dicas & truques de programação mais populares |
|
Java - Estruturas de dados em Java - Como obter a quantidade de nós em uma árvore binária usando Java |
Você também poderá gostar das dicas e truques de programação abaixo |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





