 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
PHP ::: Design Patterns (Padrões de Projeto) ::: Singleton Pattern |
Como usar o padrão de projeto Singleton em suas aplicações PHPQuantidade de visualizações: 9087 vezes |
|
O padrão de projeto Singleton (ou Singleton Pattern) é um dos padrões de projeto mais conhecidos e implementados extensivamente nas linguagens Java e C#. Como o PHP, a partir de sua versão 5, suporta praticamente todos os recursos da programação orientada a objetos, este padrão pode ser implementado também nesta linguagem sem muitas dificuldades. Uma das situações nas quais usamos o padrão Singleton é quando queremos que somente uma instância de uma determinada classe seja criada e que esta esteja disponível para todas as demais classes do sistema. Um exemplo disso é uma classe responsável por registrar logs do sistema, uma classe responsável por obter conexões com o banco de dados, ou ainda uma classe que concentra dados de configuração da aplicação. Assim, a chave do padrão Singleton é um método estático, geralmente chamado de getInstance(), que retorna uma nova instância da classe se esta ainda não foi instanciada. Se a classe já tiver sido instanciada, o método getInstance() retorna a instância já existente. Vamos ver um exemplo deste padrão em PHP. Observe o código a seguir:
<?
// Uma classe Singleton responsável por gravar
// logs no sistema
class Logger{
// variável estática e privada que guarda a instância
// atual da classe
private static $instancia = NULL;
// Método estático que retorna uma instância já existente, ou
// cria uma nova instância
public static function getInstance(){
if(self::$instancia == NULL){
self::$instancia = new Logger();
}
return self::$instancia;
}
// Construtor privado para evitar que instâncias sejam
// criadas usando new
private function __construct(){
// não precisamos fazer nada aqui
}
// Método clone() também privado para evitar a criação
// de clones desta classe
private function __clone(){
// não precisamos fazer nada aqui
}
public function registrarLog($dados){
echo "Vou registrar o log: " . $dados;
}
}
// vamos registrar um novo log usando a classe Singleton
Logger::getInstance()->registrarLog("Novo usuário cadastrado.");
?>
Ao executar este código teremos o seguinte resultado: Vou registrar o log: Novo usuário cadastrado. |
Java ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como criar e inicializar um vetor de strings em JavaQuantidade de visualizações: 45409 vezes |
|
Nesta dica mostrarei como podemos declarar, criar e inicializar os valores dos elementos de um array (vetor) de strings na linguagem Java. Em seguida nós usaremos o laço for melhorado do Java para exibir os elementos do vetor. Veja o código completo para o exemplo:
public class Estudos{
public static void main(String[] args){
// cria um array de cinco elementos
String[] pessoas = {"Fábio", "Fernanda",
"Francisco", "João", "Osmar"};
// exibe os valores usando o for
// melhorado (enhanced for loop) da
// versão 5.0
for(String pessoa: pessoas){
System.out.println(pessoa);
}
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Fábio Fernanda Francisco João Osmar Lembre-se de que vetor e array são as mesmas coisas. Em algumas situações, um array pode também ser chamado de matriz. |
VB.NET ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a equação reduzida da reta em VB.NET dados dois pontos pertencentes à retaQuantidade de visualizações: 451 vezes |
|
Nesta dica de VB.NET veremos como calcular a equação reduzida da reta quando temos dois pontos pertencentes à esta reta. Não, nessa dica não vamos calcular a equação geral da reta, apenas a equação reduzida. Em outras dicas do site você encontra como como isso pode ser feito. Para relembrar: a equação reduzida da reta é y = mx + n, em que x e y são, respectivamente, a variável independente e a variável dependente; m é o coeficiente angular, e n é o coeficiente linear. Além disso, m e n são números reais. Com a equação reduzida da reta, é possível calcular quais são os pontos que pertencem a essa reta e quais não pertencem. Vamos começar então analisando a seguinte figura, na qual temos dois pontos que pertencem à uma reta: 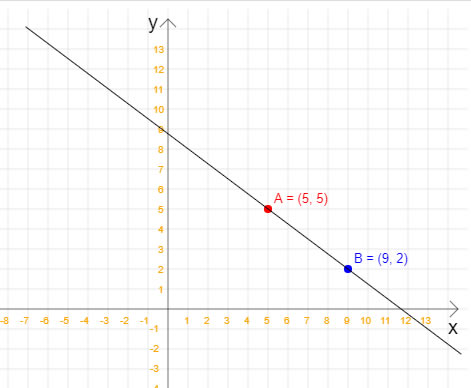 Note que a reta da figura passa pelos pontos A(5, 5) e B(9, 2). Então, uma vez que já temos os dois pontos, já podemos calcular a equação reduzida da reta. Veja o código VB.NET completo para esta tarefa:
Imports System
Module Program
' função principal do programa VB.NET
Sub Main(args As String())
' vamos ler as coordenadas do primeiro ponto
Console.Write("Coordenada x do primeiro ponto: ")
Dim x1 As Double = Double.Parse(Console.ReadLine())
Console.Write("Coordenada y do primeiro ponto: ")
Dim y1 As Double = Double.Parse(Console.ReadLine())
' vamos ler as coordenadas do segundo ponto
Console.Write("Coordenada x do segundo ponto: ")
Dim x2 As Double = Double.Parse(Console.ReadLine())
Console.Write("Coordenada y do segundo ponto: ")
Dim y2 As Double = Double.Parse(Console.ReadLine())
Dim sinal As String = "+"
' vamos calcular o coeficiente angular da reta
Dim m As Double = (y2 - y1) / (x2 - x1)
' vamos calcular o coeficiente linear
Dim n As Double = y1 - (m * x1)
' coeficiente linear menor que zero? O sinal será negativo
If n < 0 Then
sinal = "-"
n = n * -1
End If
' mostra a equação reduzida da reta
Console.WriteLine("Equação reduzida: y = " & m & "x" _
& " " & sinal & " " & n)
Console.WriteLine(vbCrLf & vbCrLf & "Pressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código VB.NET nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 5 Coordenada y do primeiro ponto: 5 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 2 Equação reduzida: y = -0,75x + 8,75 Para testarmos se nossa equação reduzida da reta está realmente correta, considere o valor 3 para o eixo x da imagem acima. Ao efetuarmos o cálculo: >> y = (-0.75 * 3) + 8.75 y = 6.5000 temos o valor 6.5 para o eixo y, o que faz com que o novo ponto caia exatamente em cima da reta considerada na imagem. |
Java ::: Dicas & Truques ::: Data e Hora |
Datas e horas em Java - Como obter o dia do mês usando as constantes DATE e DAY_OF_MONTH da classe CalendarQuantidade de visualizações: 9222 vezes |
Em algumas situações pode ser necessário obtermos o dia do mês para uma determinada data. Nestes casos podemos usar o método get() em combinação com as constantes DATE e DAY_OF_MONTH da classe Calendar. Estas constantes retornam um valor inteiro na faixa de 1 a 31. Veja um exemplo:
package arquivodecodigos;
import java.util.*;
public class Estudos{
public static void main(String args[]){
// vamos obter a data e hora atual
Calendar agora = Calendar.getInstance();
// vamos obter o dia do mês
System.out.println("O dia do mês é: " +
agora.get(Calendar.DAY_OF_MONTH));
}
}
Ao executarmos este código nós teremos o seguinte resultado: O dia do mês é: 26 |
Java ::: Dicas & Truques ::: Ordenação e Pesquisa (Busca) |
Como usar a pesquisa ou busca linear ou sequencial nos elementos de um vetor em JavaQuantidade de visualizações: 4872 vezes |
|
A busca linear ou sequencial, muitas vezes chamada de pesquisa linear ou sequencial, é geralmente implementada por meio de um algorítmo que varre os elementos de um coleção sequencial, começando do primeiro elemento e indo até o último. Esta busca não é tão usada quando a pesquisa binária ou hashing, por ser considerada muito lenta quando aplicado a um conjunto de dados muito grande. A busca linear ou sequencial em um vetor Java pode ser descrito pelos seguintes passos: 1) Efetua a varredura dos elementos do vetor. 2) Compara o valor do elemento atual do vetor com o valor sendo pesquisado. 3) Se o valor for encontrado, efetue o procedimento desejado com o elemento do vetor. 4) Se a varredura alcançar o último elemento do vetor e o valor pesquisado não for encontrado, exiba uma mensagem de erro ou algum outro procedimento para alertar o usuário do programa. Veja um exemplo no qual declaramos e preenchemos um vetor de int com 5 elementos e em seguida usamos um método pesquisaLinear para verificar se um determinado valor existe no vetor:
package arquivodecodigos;
public class Estudos{
public static void main(String a[]){
// vamos criar um vetor de 5 elementos int
int[] valores = {32, 7, 21, 4, 90};
// vamos pesquisar o valor 21
int valor = 21;
// vamos verifiar se o valor está no vetor
int indice = pesquisaLinear(valores, valor);
if(indice > -1){
System.out.println("O valor foi encontrado no índice: "
+ indice);
}
else{
System.out.println("O valor não foi encontrado.");
}
}
// método que permite efetuar a busca linear em um vetor
public static int pesquisaLinear(int[] vetor, int valor){
// percorre os elementos do vetor
for(int i = 0; i < vetor.length; i++){
// o valor foi encontrado?
if(vetor[i] == valor){
return i;
}
}
// não foi encontrado? vamos retornar -1
return -1;
}
}
Ao executarmos este código nós teremos o seguinte resultado: O valor foi encontrado no índice: 2 Veja o mesmo código sem usar um método adicional, ou seja, a busca linear é feito dentro do método main() da classe Java:
package arquivodecodigos;
public class Estudos{
public static void main(String a[]){
// vamos criar um vetor de 5 elementos int
int[] valores = {32, 7, 21, 4, 90};
// vamos pesquisar o valor 21
int valor = 21;
// vamos verifiar se o valor está no vetor
int indice = -1; // não foi encontrado
// percorre os elementos do vetor
for(int i = 0; i < valores.length; i++){
// o valor foi encontrado?
if(valores[i] == valor){
indice = i;
break;
}
}
if(indice > -1){
System.out.println("O valor foi encontrado no índice: "
+ indice);
}
else{
System.out.println("O valor não foi encontrado.");
}
}
}
|
Ruby ::: Dicas & Truques ::: Strings e Caracteres |
Como inserir uma substring em uma determinada posição de uma string em Ruby usando a função insert()Quantidade de visualizações: 9027 vezes |
|
Muita vezes precisamos inserir uma substring em uma determinada posição de uma string em Ruby. Esta tarefa pode ser realizada com a função insert() da classe String. Esta função opera na string original e requer dois argumentos: a posição na string onde a substring será inserida e a substring propriamente dita. A posição é um índice iniciando em 0. Índices negativos são contados a partir do final da string. Veja o exemplo: # declara e inicializa uma variável string frase = "Gosto muito de Ruby" puts "A frase original é: " + frase # vamos inserir " Python e" antes de "Ruby". frase.insert(14, " Python e") # exibe o resultado puts "A nova frase é: " + frase Ao executar este código Ruby nós teremos o seguinte resultado: A frase original é: Gosto muito de Ruby A nova frase é: Gosto muito de Python e Ruby |
Java ::: Dicas & Truques ::: Matemática e Estatística |
Como calcular juros simples e composto - Calculando juros simples e montante na linguagem JavaQuantidade de visualizações: 14485 vezes |
|
O regime de juros será simples quando o percentual de juros incidir apenas sobre o valor principal. Sobre os juros gerados a cada período não incidirão novos juros. Valor Principal, ou simplesmente principal, é o valor inicial emprestado ou aplicado, antes de somarmos os juros. Transformando em fórmula temos: J = P . i . n Onde: J = juros P = principal (capital) i = taxa de juros n = número de períodos Imaginemos uma dívida de R$ 2.000,00 que deverá ser paga com juros de 5% a.m. pelo regime de juros simples e o prazo para o pagamento é de 2 meses. O cálculo em Java pode ser feito assim:
public class Estudos{
public static void main(String args[]){
double principal = 2000.00;
double taxa = 0.08;
int meses = 2;
double juros = principal * taxa * meses;
System.out.println("O total de juros a ser pago é: "
+ juros);
System.exit(0);
}
}
O montante da dívida pode ser obtido das seguintes formas: a) Montante = Principal + Juros b) Montante = Principal + (Principal x Taxa de juros x Número de períodos) M = P . (1 + (i . n)) Veja o código:
public class Estudos{
public static void main(String args[]){
double principal = 2000.00;
double taxa = 0.08;
int meses = 2;
double juros = principal * taxa * meses;
double montante = principal * (1 + (taxa * meses));
System.out.println("O total de juros a ser pago é: "
+ juros);
System.out.println("O montante a ser pago é: "
+ montante);
System.exit(0);
}
}
|
Delphi ::: Dicas & Truques ::: Recursão (Recursividade) |
Como calcular fatorial em Delphi usando recursividadeQuantidade de visualizações: 13261 vezes |
|
O fatorial de um determinado número, representado por n! equivale a multiplicar este número por seus antecessores. Assim, o fatorial de 4 (4!) pode ser calculado da seguinte forma: 4 x 3 x 2 x 1 = 24 Sempre que falamos de recursão, o cálculo de fatorial nos auxilia na exemplicação por ser relativamente fácil de se entender todas as etapas do processo. O código abaixo mostra uma função recursiva em Delphi que calcula o fatorial de qualquer número. Tenha cuidado. Calcular o fatorial de um número maior que 10 pode tornar sua máquina extremamente lenta, além de, muitas vezes, não retornar os resultados esperados.
// função recursiva para calcular o fatorial
// de um determinado número
function fatorial(n: Integer): Integer;
begin
if n = 0 then
Result := 1
else
Result := n * fatorial(n - 1);
end;
// vamos chamar a função recursiva
// a partir do Click de um botão
procedure TForm1.Button1Click(Sender: TObject);
var
res: Integer;
begin
// vamos calcular o fatorial de 5
res := fatorial(5);
// vamos mostrar o resultado
ShowMessage('O fatorial de 5 é: ' + IntToStr(res));
end;
Para fins de compatibilidade, esta dica foi escrita usando Delphi 2009. |
Delphi ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em Delphi dados dois pontos no plano cartesianoQuantidade de visualizações: 1412 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem Delphi que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
procedure TForm4.Button2Click(Sender: TObject);
var
x1, y1, x2, y2, m: Double;
begin
// x e y do primeiro ponto
x1 := 3;
y1 := 6;
// x e y do segundo ponto
x2 := 9;
y2 := 10;
// agora vamos calcular o coeficiente angular
m := (y2 - y1) / (x2 - x1);
// e mostramos o resultado
Memo1.Lines.Add('O coeficiente angular é: ' +
FloatToStr(m));
end;
Ao executar este código em linguagem Delphi nós teremos o seguinte resultado: O coeficiente angular é: 0,666666666666667 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
procedure TForm4.Button2Click(Sender: TObject);
var
x1, y1, x2, y2, tangente: Double;
cateto_oposto, cateto_adjascente, tetha: Double;
begin
// incluir a unit Math
// x e y do primeiro ponto
x1 := 3;
y1 := 6;
// x e y do segundo ponto
x2 := 9;
y2 := 10;
// vamos obter o comprimento do cateto oposto
cateto_oposto := y2 - y1;
// e agora o cateto adjascente
cateto_adjascente := x2 - x1;
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
tetha := ArcTan2(cateto_oposto, cateto_adjascente);
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
tangente := Tan(tetha);
// e mostramos o resultado
Memo1.Lines.Add('O coeficiente angular é: ' +
FloatToStr(tangente));
end;
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Java ::: Dicas & Truques ::: Programação Orientada a Objetos |
Programação Orientada a Objetos em Java - Java OOP - Como chamar o construtor de uma superclasse a partir da classe derivadaQuantidade de visualizações: 19317 vezes |
|
Em algumas situações, é necessário efetuar uma chamada ao construtor de uma superclasse a partir da sub-classe, ou classe derivada. Principalmente quando temos que inicializar dados privados pertencentes à superclasse. Imaginemos o seguinte cenário: uma classe Pessoa cujo construtor recebe o nome e idade da pessoa. Temos então uma classe Aluno que herda de pessoa e cujo construtor recebe nome, idade e matrícula. Desta forma, temos aqui uma boa oportunidade para efetuarmos uma chamada ao construtor da superclasse a partir da classe derivada. Comece criando a classe Pessoa (Pessoa.java):
public class Pessoa{
public String nome;
public int idade;
// construtor da classe
public Pessoa(String nome, int idade){
this.nome = nome;
this.idade = idade;
}
}
Compile Pessoa.java. Agora vamos criar um classe Aluno (Aluno.java) que herda da classe Pessoa:
public class Aluno extends Pessoa{
public String matricula;
// construtor
public Aluno(String nome, int idade,
String matricula){
// chama o construtor da superclasse
super(nome, idade);
this.matricula = matricula;
}
}
Compile Aluno.java e escreva o programa abaixo, que demonstra como a chamada ao construtor da superclasse é feita a partir da subclasse, ou classe derivada:
public class Estudos{
public static void main(String args[]){
// cria um objeto da classe Aluno
Aluno aluno = new Aluno("Osmar J. Silva",
36, "AC434-23");
// Exibe o resultado
System.out.println("Nome: " + aluno.nome + "\n" +
"Idade: " + aluno.idade + "\n" +
"Matrícula: " + aluno.matricula);
}
}
Execute este código e observe alguns detalhes interessantes. O mais importante é a forma de chamar o construtor da superclasse: // chama o construtor da superclasse super(nome, idade); Veja como recebemos três variáveis no construtor da classe Aluno e passamos duas delas para o construtor da superclasse. |
Nossas 20 dicas & truques de programação mais populares |
|
C - Como escrever uma função is_numeric() em C que verifica se uma string contém apenas dígitos de 0 a 9 JavaScript - Como remover todos os espaços de uma string em JavaScript usando uma função personalizada remover_espacos() JavaScript - Como usar objetos Set em seus códigos JavaScript |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Java - Padrões de projeto para iniciantes - Como usar o padrão de projeto Singleton em suas aplicações Java Java - Como retornar a quantidade de mapeamentos (chave-valor) em um HashMap do Java usando o método size() |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




