 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
C# ::: Windows Forms ::: ComboBox |
Como retornar a quantidade de itens em um ComboBox do C# Windows FormsQuantidade de visualizações: 9518 vezes |
|
A quantidade de elementos (ou itens) em um ComboBox do C# Windows Forms pode ser obtida por meio da propriedade Count da classe ComboBox.ObjectCollection. Podemos ter acesso a esta classe a partir da propriedade Items da classe ComboBox. Veja um trecho de código no qual obtemos a quantidade de itens em um ComboBox chamado cidades:
private void button1_Click(object sender, EventArgs e){
int quant = cidades.Items.Count;
MessageBox.Show("O ComboBox contém " + quant + " itens");
}
|
JavaScript ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o seno de um número ou ângulo em JavaScript usando a função sin() do objeto MathQuantidade de visualizações: 8988 vezes |
|
Em geral, quando falamos de seno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função seno disponível nas linguagens de programação para calcular o seno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função seno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o seno é a razão entre o cateto oposto (oposto ao ângulo theta) e a hipotenusa, ou seja, o cateto oposto dividido pela hipotenusa. Veja a fórmula: \[\text{Seno} = \frac{\text{Cateto oposto}}{\text{Hipotenusa}} \] Então, se dividirmos 20 por 36.056 (na figura eu arredondei) nós teremos 0.5547, que é a razão entre o cateto oposto e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.5547. O resultado será 0.9828 (em radianos). Convertendo 0.9828 radianos para graus, nós obtemos 56.31º, que é exatamente o ângulo em graus entre o cateto oposto e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é seno na trigonometria, vamos entender mais sobre a função sin() da linguagem JavaScript. Esta função, disponível no objeto Math, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja:
<html>
<head>
<title>Estudos JavaScript</title>
</head>
<body>
<script type="text/javascript">
// vamos calcular o seno de três números
document.writeln("Seno de 0 = " + Math.sin(0));
document.writeln("<br>Seno de 1 = " + Math.sin(1));
document.writeln("<br>Seno de 2 = " + Math.sin(2));
</script>
</body>
</html>
Ao executar este código JavaScript nós teremos o seguinte resultado: Seno de 0 = 0 Seno de 1 = 0.8414709848078965 Seno de 2 = 0.9092974268256817 Note que calculamos os senos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função seno mostrada abaixo: 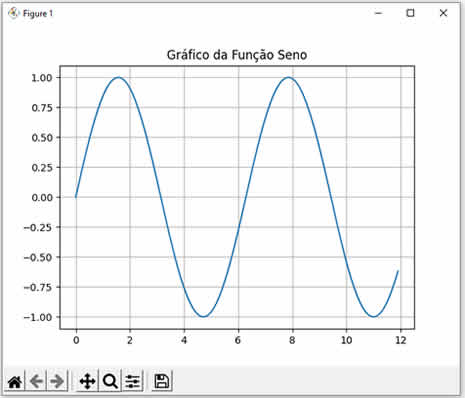 |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de Java - Escreva um programa Java que leia e apresente um conjunto de números inteiros para uma matriz bidimensional 2 x 4 e apresente o valor e a posiçãoQuantidade de visualizações: 528 vezes |
|
Pergunta/Tarefa: Escreva um programa Java que leia e apresente um conjunto de números inteiros para uma matriz bidimensional 2 x 4 e apresente o valor e a posição do maior número inteiro. Você deverá informar tanto a linha quanto a coluna que o maior valor é encontrado. Uma matriz bidimensional 2 x 4 quer dizer que a matriz possui 2 linhas e 4 colunas. Seu programa Java deverá exibir uma saída parecida com:
Valor da linha 1 e coluna 1: 6
Valor da linha 1 e coluna 2: 9
Valor da linha 1 e coluna 3: 11
Valor da linha 1 e coluna 4: 5
Valor da linha 2 e coluna 1: 20
Valor da linha 2 e coluna 2: 63
Valor da linha 2 e coluna 3: 31
Valor da linha 2 e coluna 4: 7
Valores na matriz
6 9 11 5
20 63 31 7
O maior valor é 63
Ele foi encontrado na linha 2 e coluna 2
Veja a resolução comentada deste exercício usando Java:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
// variaveis usdas na resolução do problema
int matriz[][] = new int[2][4];
int maior_valor, linha, coluna;
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// vamos ler os valores e colocar na matriz
for(int i = 0; i < matriz.length; i++){ // linhas
for(int j = 0; j < matriz[0].length; j++){ // colunas
System.out.print("Valor da linha " + (i + 1) + " e coluna "
+ (j + 1) + ": ");
matriz[i][j] = Integer.parseInt(entrada.nextLine());
}
System.out.println();
}
// vamos mostrar a matriz da forma que ela foi informada
System.out.println("\nValores na matriz\n");
for(int i = 0; i < matriz.length; i++){ // linhas
for(int j = 0; j < matriz[0].length; j++){ // colunas
System.out.printf("%5d", matriz[i][j]);
}
// passa para a próxima linha da matriz
System.out.println();
}
// agora vamos localizar o maior valor na matriz
linha = 0;
coluna = 0;
maior_valor = matriz[linha][coluna];
for(int i = 0; i < matriz.length; i++){ // linhas
for(int j = 0; j < matriz[0].length; j++){ // colunas
if(matriz[i][j] > maior_valor){
maior_valor = matriz[i][j];
linha = i + 1;
coluna = j + 1;
}
}
}
// vamos mostrar o resultado
System.out.println("\nO maior valor é " + maior_valor);
System.out.println("Ele foi encontrado na linha " + linha +
" e coluna " + coluna);
}
}
|
C# ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Como usar a instrução continue da linguagem C#Quantidade de visualizações: 9333 vezes |
A instrução continue é usada quando queremos abandonar completamente a iteração atual de um laço e saltar imediatamente para a próxima iteração. Veja um exemplo:
static void Main(string[] args){
for(int i = 0; i <= 10; i++){
// se o valor de i não for par, vamos passar
// para a próxima iteração
if(i % 2 != 0)
continue;
Console.WriteLine("{0}", i);
}
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
Aqui nós estamos exibindo somente os números pares de 0 a 10. Note que, cada vez que o valor de i for ímpar, nós usamos a instrução continue para interromper a instrução atual e saltar para a próxima. Veja mais um exemplo, desta vez usando um laço while:
static void Main(string[] args){
int valor = 0;
while(valor <= 10){
if((valor >= 5) && (valor <= 7)){
valor++;
continue;
}
Console.WriteLine("{0}", valor);
valor++;
}
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
Este laço conta de 0 a 10 mas não exibe os valores 5, 6 e 7. |
GNU Octave ::: Desafios e Lista de Exercícios Resolvidos ::: Pesquisa Operacional |
Exercício Resolvido de Octave - Programação Linear - Um fazendeiro decidiu misturar duas rações, a Ração X e a Ração Y. Cada porção de ração dada aos animaisQuantidade de visualizações: 451 vezes |
|
Pergunta/Tarefa: Este exercício de Octave aborda o uso da função glpk() para resolver um problema de Pesquisa Operacional usando Programação Linear. 1) Um fazendeiro decidiu misturar duas rações, a Ração X e a Ração Y. Cada porção de ração dada aos animais exige 60g de proteína e 30g de gordura. A Ração X possui 15g de proteína e 10g de gordura, e custa R$ 80,00 a unidade. A Ração Y apresenta 20g de proteína e 5g de gordura e custa R$ 50,00 a unidade. Quanto de cada ração deve ser usada para minimizar os custos do fazendeiro? Sua saída deverá ser parecida com: A solução para o problema de minimização é: x = 2.40 y = 1.20 O custo mínimo é: 252.00 Antes de passarmos ao código Octave, vamos fazer a modelagem matemática do problema. O primeiro passo é identificar as variáveis. Assim, vamos chamar de x o número de unidades da Ração X e de y o número de unidades da Ração Y. Veja: x = Número de unidades da Ração X y = Número de unidades da Ração Y E então temos a função custo: custo = 80x + 50y A primeira restrição diz respeito à quantidade de proteína em cada porção de ração. Sabendo que a Ração X apresenta 15g de proteína e a Ração Y apresenta 20g de proteína nós temos: R1: 15x + 20y >= 60 (proteína) A segunda restrição diz respeito à quantidade de gordura em cada porção de ração. Sabendo que a Ração X apresenta 10g de gordura e a Ração Y apresenta 5g de gordura nós temos: R2: 10x + 5y >= 30 (gordura) As restrições R3 e R4 dizem respeito à não negatividade das variáveis de decisão: R3: x >= 0 R4: y >= 0 Veja agora o código Octave completo (pesquisa_operacional.m):
# vamos começar definindo a matriz que representa a função de
# minimização
c = [80.0, 50.0]';
# agora a matriz de restrições
A = [15, 20; 10, 5];
b = [60, 30]';
# as restrições de não negatividade e o limite superior
lb = [0, 0]';
ub = [];
# definimos as restrições como limites inferiores
ctype = "LL";
# indicamos que vamos usar variáveis contínuas (não inteiros)
vartype = "CC";
# vamos usar minimização, por isso definimos o valor 1. Se fosse
# maximização o valor seria -1
s = 1;
# definimos os parâmetros adicionais
param.msglev = 1;
param.itlim = 100;
# e chamamos a função glpk()
[xmin, fmin, status, extra] = glpk(c, A, b, lb, ub, ctype, vartype, s, param);
# mostramos a solução para o problema de minimização
printf("A solução para o problema de minimização é:\n\n");
printf("x = %.2f\n", xmin(1));
printf("y = %.2f\n", xmin(2));
# para finalizar vamos mostrar o custo mínimo
printf("\nO custo mínimo é: %.2f\n\n", fmin);
Ao executar o código você perceberá que, para minimizar os custos do fazendeiro, deverão ser usados na mistura 2,4 unidades da Ração X e 1,2 unidades da Raça Y, a um custo mínimo de R$ 252,00. |
C ::: Dicas & Truques ::: Matemática e Estatística |
Como elevar uma base a um determinado expoente usando a função pow() da linguagem CQuantidade de visualizações: 3426 vezes |
Em algumas situações nós precisamos efetuar cálculos de potenciação em C, ou seja, elevar um número (uma base) a um determinado expoente e obter sua potência. Veja a figura a seguir: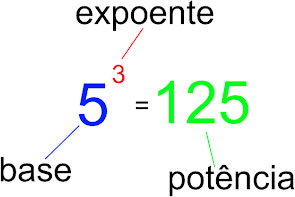 Veja que aqui o valor 5 foi elevado ao cubo, ou seja, ao expoente 3 e obtemos como resultado sua potência: 125. A linguagem C nos fornece a função pow(), presente no header math.h que recebe como argumentos a base e o expoente e nos retorna a potência (como um valor double). Veja um exemplo de seu uso no código abaixo:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
int base = 4;
int expoente = 5;
double potencia = pow(4, 5);
printf("A base %d elevada ao expoente %d é igual à potência %f\n\n",
base, expoente, potencia);
system("PAUSE");
return 0;
}
Ao executarmos este código C nós teremos o seguinte resultado: A base 4 elevada ao expoente 5 é igual à potência 1024.000000 Note que a função pow() da linguagem C retorna um valor double. |
Java ::: Estruturas de Dados ::: Lista Ligada Simples |
Estruturas de dados em Java - Introdução às listas ligadas em JavaQuantidade de visualizações: 16296 vezes |
|
Então você se interessou pelo assunto de listas ligadas em Java? Recomendo que leia esta anotação com muita atenção. É o ponto de partida para o entendimento e implementação desta estrutura de dados tão importante. Uma lista singularmente ou duplamente ligada (singly or doubly linked list) é uma lista dinâmica no sentido de que ela pode crescer ou diminuir de acordo com as necessidades do programa. As matrizes (arrays) comuns também têm seu papel assegurado no estudo das estruturas de dados. No entanto, uma de suas limitações é que seus elementos são dispostos lado a lado na memória. Isso torna a inserção de um novo elemento no meio do array uma tarefa dispendiosa, visto que os demais elementos precisam ser movidos para outras posições. Em uma lista dinâmica isso não acontece. O conceito principal das listas ligadas é a capacidade de um nó (cada elemento da lista é chamado de nó) poder apontar para um outro nó com estrutura semelhante. Veja a estrutura típica de um nó em uma lista ligada:
// classe No
public class No{
public int valor;
public No proximo;
}
// fim da classe No
Note que esta classe contém dois campos: um campo do tipo int que guarda o valor do nó e um campo do tipo referência apontando para um objeto do mesmo tipo que o nó atual. Isso permite a circularidade das listas, ou seja, um nó apontando para um elemento de seu mesmo tipo. Com este conhecimento já podemos criar o início de uma lista singularmente ligada, para isso só precisamos declarar uma variável do tipo No. Veja: // declara o início da lista No inicio; Até agora temos uma lista ligada vazia. A criação do primeiro elemento da lista pode ser feito da seguinte forma:
public class Lista{
// declara o início da lista
static No inicio = null;
public static void main(String args[]){
// verifica se a lista está vazia
if(inicio == null){
// reserva memória para o novo nó
inicio = new No();
// a memória foi alocada com sucesso?
if(inicio != null){
inicio.valor = 150;
// é o primeiro nó...seu campo proximo não deve
// apontar para lugar nenhum
inicio.proximo = null;
}
}
System.out.println(inicio.valor);
System.exit(0);
}
}
Aqui nós temos a criação do primeiro nó de uma lista singularmente ligada. Note como usamos a palavra-chave new para alocar memória para o nó atual. Veja também que o valor null é fornecido para o campo próximo do nó. Isso aconteceu porque temos apenas um nó. Em outras dicas desta seção abordaremos como inserir os demais nós e também listar todos os nós existentes na lista. Até lá. |
Java ::: Dicas & Truques ::: Programação Orientada a Objetos |
Programação Orientada a Objetos em Java - Java OOP - Como chamar o construtor de uma superclasse a partir da classe derivadaQuantidade de visualizações: 19316 vezes |
|
Em algumas situações, é necessário efetuar uma chamada ao construtor de uma superclasse a partir da sub-classe, ou classe derivada. Principalmente quando temos que inicializar dados privados pertencentes à superclasse. Imaginemos o seguinte cenário: uma classe Pessoa cujo construtor recebe o nome e idade da pessoa. Temos então uma classe Aluno que herda de pessoa e cujo construtor recebe nome, idade e matrícula. Desta forma, temos aqui uma boa oportunidade para efetuarmos uma chamada ao construtor da superclasse a partir da classe derivada. Comece criando a classe Pessoa (Pessoa.java):
public class Pessoa{
public String nome;
public int idade;
// construtor da classe
public Pessoa(String nome, int idade){
this.nome = nome;
this.idade = idade;
}
}
Compile Pessoa.java. Agora vamos criar um classe Aluno (Aluno.java) que herda da classe Pessoa:
public class Aluno extends Pessoa{
public String matricula;
// construtor
public Aluno(String nome, int idade,
String matricula){
// chama o construtor da superclasse
super(nome, idade);
this.matricula = matricula;
}
}
Compile Aluno.java e escreva o programa abaixo, que demonstra como a chamada ao construtor da superclasse é feita a partir da subclasse, ou classe derivada:
public class Estudos{
public static void main(String args[]){
// cria um objeto da classe Aluno
Aluno aluno = new Aluno("Osmar J. Silva",
36, "AC434-23");
// Exibe o resultado
System.out.println("Nome: " + aluno.nome + "\n" +
"Idade: " + aluno.idade + "\n" +
"Matrícula: " + aluno.matricula);
}
}
Execute este código e observe alguns detalhes interessantes. O mais importante é a forma de chamar o construtor da superclasse: // chama o construtor da superclasse super(nome, idade); Veja como recebemos três variáveis no construtor da classe Aluno e passamos duas delas para o construtor da superclasse. |
Delphi ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como declarar e inicializar uma matriz de Integer em DelphiQuantidade de visualizações: 12421 vezes |
Nesta dica eu mostrarei como declarar e inicializar uma matriz de inteiros (Integer) em Delphi. Mostrarei também como exibir o valor de cada elemento usando um laço For. Veja o código:
procedure TForm3.Button1Click(Sender: TObject);
var
// vamos declarar uma matriz de 10 inteiros
valores: array[1..10] of Integer;
i: Integer;
begin
// vamos inicializar a matriz com os números pares de 2 até 20
for i := Low(valores) to High(valores) do
begin
valores[i] := i * 2;
end;
// vamos exibir os valores dos elementos
for i := Low(valores) to High(valores) do
begin
Memo1.Lines.Add(IntToStr(valores[i]));
end;
end;
Ao executar este código teremos o seguinte resultado: 2 4 6 8 10 12 14 16 18 20 |
C ::: Dicas & Truques ::: Matemática e Estatística |
Como calcular raiz quadrada em C usando a função sqrt()Quantidade de visualizações: 6869 vezes |
A raiz quadrada de um número pode ser obtida em C por meio da função sqrt(). Esta função recebe um valor double, ou seja, qualquer tipo que possa ser convertido em double e retorna um valor double. Veja o exemplo:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(int argc, char *argv[])
{
int numero = 9;
printf("A raiz quadrada de %d é %f", numero,
sqrt(numero));
printf("\n\n");
system("pause");
return 0;
}
Ao executar este código nós teremos o seguinte resultado: A raiz quadrada de 9 é 3. É importante observar que não é possível obter a raiz quadrada de um número negativo. Caso seu código tente fazer isso, o resultado poderá ser imprevisível. |
Nossas 20 dicas & truques de programação mais populares |
Você também poderá gostar das dicas e truques de programação abaixo |
|
JavaScript - JavaScript para iniciantes - Como usar o método escape() para codificar uma frase em JavaScript Android Java - Como detectar um clique em um botão do Android usando setOnClickListener() e exibir uma mensagem AlertDialog |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




