 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
Java ::: Pacote java.awt.image ::: BufferedImage |
Como desenhar um BufferedImage em um JComponent do JavaQuantidade de visualizações: 10970 vezes |
Neste exemplo nós usamos o método drawImage() da classe Graphics para desenhar o conteúdo de um BufferedImage (que contém uma imagem JPG) em uma JFrame do Java Swing:
import java.awt.*;
import java.io.*;
import java.awt.image.*;
import java.awt.event.*;
import javax.swing.*;
import javax.imageio.*;
public class Estudos extends JFrame{
private BufferedImage imagem;
public Estudos(){
super("Estudos Java");
Container c = getContentPane();
c.setLayout(new FlowLayout());
JButton btn = new JButton("Carregar Imagem");
btn.addActionListener(
new ActionListener(){
public void actionPerformed(ActionEvent e){
imagem = null;
try{
imagem = ImageIO.read(
new File("imagens/fundo.jpg"));
}
catch(IOException exc){
JOptionPane.showMessageDialog(null,
"Erro ao carregar a imagem: " +
exc.getMessage());
}
if(imagem != null){
desenhar();
}
}
}
);
c.add(btn);
setSize(400, 300);
setVisible(true);
}
public void desenhar(){
// desenha a imagem no JFrame
Graphics g = getGraphics();
g.drawImage(imagem, 0, 0, this);
}
public static void main(String args[]){
Estudos app = new Estudos();
app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
}
|
Java ::: Java para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular o produto escalar entre dois vetores usando Java - Geometria Analítica e Álgebra Linear usando JavaQuantidade de visualizações: 3564 vezes |
|
O produto escalar (em inglês: dot product) entre dois vetores é um número real que relaciona o comprimento desses dois vetores e o ângulo formado por eles. É importante notar que alguns autores se referem ao produto escalar como produto interno. Obtém-se o produto escalar entre dois vetores, no R2, ou três vetores, no R3, por meio da fórmula a seguir (assumindo dois vetores __$\vec{u} = (a, b)__$ e __$\vec{v} = (c, d)__$ no R2). \[\vec{u} \cdot \vec{v} = a \cdot c + b \cdot d \] Vamos agora a um exemplo prático. Veja a imagem abaixo, na qual temos dois vetores, com suas coordenadas e magnitudes (módulo, comprimento ou norma): 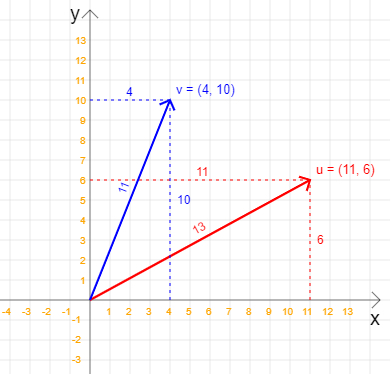 Note que ambos os vetores possuem como origem as coordenadas (0, 0). O primeiro vetor possui as coordenadas finais (4, 10) e magnitude 11, e o segundo vetor possui as coordenadas finais (11, 6) e magnitude 13. Magnitude é o tamanho do vetor, ou seja, seu comprimento, seu módulo ou norma. Veja agora o código Java completo que lê as coordenadas dos dois vetores e calcula e mostra o produto escalar entre eles:
package arquivodecodigos;
import java.util.Scanner;
public class Estudos{
public static void main(String[] args){
Scanner entrada = new Scanner(System.in);
// x e y do primeiro vetor
System.out.print("Coordenada x do primeiro vetor: ");
float x1 = Float.parseFloat(entrada.nextLine());
System.out.print("Coordenada y do primeiro vetor: ");
float y1 = Float.parseFloat(entrada.nextLine());
// x e y do segundo ponto
System.out.print("Coordenada x do segundo vetor: ");
float x2 = Float.parseFloat(entrada.nextLine());
System.out.print("Coordenada y do segundo vetor: ");
float y2 = Float.parseFloat(entrada.nextLine());
// vamos calcular o produto escalar
float pEscalar = (x1 * x2) + (y1 * y2);
// mostramos o resultado
System.out.println("O produto escalar é: " + pEscalar);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Coordenada x do primeiro vetor: 4 Coordenada y do primeiro vetor: 10 Coordenada x do segundo vetor: 11 Coordenada y do segundo vetor: 6 O produto escalar é: 104.0 |
PHP ::: Dicas & Truques ::: Variáveis e Constantes |
Como usar a função isset() do PHP para verificar se uma variável existe (foi definida)Quantidade de visualizações: 58561 vezes |
|
Em algumas situações gostaríamos de verificar se uma variável PHP foi definida, ou seja, seu valor está disponível para uso. Isso é importante para evitar efetuar algum cálculo envolvendo variáveis não existentes (que ainda não foram declaradas). Isso pode ser feito com o auxílio da função isset(). Ela retorna um valor true se a variável testada existir e não estiver com o valor NULL. Caso contrário o retorno será falso. Veja o exemplo a seguir:
<?
/*
Este trecho de código mostra como como verificar
se uma determinada variável foi definida. Esta
técnica é muito usada para verificar variáveis
fornecidas via GET ou POST.
Veja que a função isset apenas verifica se a variável
foi definida, ela não verifica se a variável contém algum
valor (no caso de GET ou POST)
*/
if(isset($_GET['cliente']))
echo "A variável cliente foi definida";
$nome = "Osmar J. Silva";
if(isset($nome))
echo 'A variável $nome foi definida';
?>
Lembre-se de que está função não verifica se a variável contém algum valor, apenas se ela existe e não sofreu atribuição do valor NULL (null em PHP). |
C# ::: Dicas & Truques ::: Data e Hora |
Como retornar o ano da data atual em C# usando a propriedade Year da classe DateTimeQuantidade de visualizações: 84 vezes |
|
Nesta dica eu mostrarei como podemos usar a propriedade Year da classe DateTime da linguagem C# para obter o ano de uma determinada data como um inteiro. Veja o código completo para o exemplo:
using System;
namespace Estudos {
class Program {
static void Main(string[] args) {
// vamos obter a data e hora atual
DateTime agora = DateTime.Now;
// e agora o ano da data como um inteiro
int ano = agora.Year;
// e finalmente mostramos o resultado
Console.WriteLine("Estamos no ano: {0}", ano);
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Estamos no ano: 2022 |
C ::: C para Engenharia ::: Física - Mecânica |
Como calcular o tempo de queda livre de um corpo dada a altura da queda e a aceleração da gravidade usando a linguagem CQuantidade de visualizações: 3007 vezes |
|
Galileu Galilei fez experimentos para comprovar que o tempo de queda dos objetos não depende de sua massa. Esse importante estudioso abandonava objetos de massas diferentes do alto da torre de Pisa e verificava que o tempo para atingirem o solo sempre era o mesmo para todos os casos. No Movimento Uniformemente Variado (MUV), o tempo de queda livre de um corpo, quando temos a altura na qual o objeto é abandonado, pode ser calculado por meio da fórmula: \[ \text{t} = \sqrt{\frac{\text{2} \cdot \text{H}}{\text{g}}} \] Onde: t ? tempo da queda (em segundos). H ? altura em metros na qual o corpo é abandonado. g ? aceleração da gravidade (m/s2). Vamos ver um exemplo? Veja o seguinte enunciado: 1) Um tijolo é largado de uma construção há 10 metros de altura. Calcule o tempo de sua queda, ou seja, o tempo imediatamente antes de o corpo (o tijolo) tocar o chão. Veja que temos a altura de 10 metros e já sabemos que a aceleração da gravidade terrestre é 9.80665. Assim, tudo que temos que fazer é jogar esses valores na fórmula. Veja o código C completo para este cálculo:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(int argc, char *argv[]){
// gravidade terrestre em m/s2
float gravidade = 9.80665;
// altura da queda
float altura = 10; // em metros
// vamos calcular o tempo da queda (em segundos)
float tempo_queda = sqrt((2 * altura) / gravidade);
// mostramos o resultado
printf("O tempo da queda livre é: %f segundos",
tempo_queda);
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: O tempo da queda livre é: 1.428087 segundos. |
C# ::: Namespace System.Windows.Forms ::: Formulários e Janelas |
Como definir uma imagem de fundo para um formulário C# Windows Forms usando a propriedade BackgroundImageQuantidade de visualizações: 14315 vezes |
|
Formulários Windows Forms podem conter uma imagem de fundo. Isso pode ser feito por meio da propriedade BackgroundImage. Em tempo de design, só precisamos clicar no formulário, acessar a janela de propriedades (Properties) e modificar o valor da propriedade BackgroundImage. Quando clicamos no botão ao lado do valor da propriedade, temos acesso à janela Select Resource. Deixe a opção Project resource file marcada e clique o botão Import. Selecione a imagem que você deseja usar e clique o botão OK. Imediatamente a imagem importada será aplicada ao fundo do formulário. É importante observar que esta forma de adicionar a imagem de fundo evita que tenhamos que enviar a imagem juntamente com nossa aplicação. Como a imagem importada fará parte do Resources da aplicação, ela será compilada e fará parte do .exe resultante. É possível também carregar uma imagem e colocá-la como fundo para um formulário em tempo de execução. Veja um trecho de código no qual carregamos uma imagem JPG localizada em uma pasta imagens no mesmo diretório do .exe da aplicação:
private void button2_Click(object sender, EventArgs e){
// using System.IO;
this.BackgroundImage = new Bitmap(Path.GetDirectoryName(
Application.ExecutablePath) + @"\imagens\foto.jpg");
}
|
Delphi ::: Classes, Controles e Componentes ::: TRegistry (Registro do Windows) |
Como excluir chaves no registro do Windows usando Delphi a função DeleteKey() da classe TRegistry do DelphiQuantidade de visualizações: 14153 vezes |
|
Em algumas situações precisamos excluir determinadas chaves do registro do Windows. Para isso podemos usar o método DeleteKey() da classe TRegistry. Este método recebe uma string especificando a chave a ser excluída e retorna um valor Boolean, informando o sucesso da operação. Veja um trecho de código no qual tentamos excluir uma chave com o nome de "Arquivo de Códigos" localizada sob a chave raiz HKEY_CURRENT_USER:
procedure TForm3.Button5Click(Sender: TObject);
var
reg: TRegistry;
begin
// uses Registry
// vamos criar uma instância da classe TRegistry
reg := TRegistry.Create;
// a chave raiz padrão é HKEY_CURRENT_USER mas, por via das dúvidas
// vamos reafirmar isso
reg.RootKey := HKEY_CURRENT_USER;
// vamos verificar se a chave que estamos querendo excluir
// existe
if reg.KeyExists('Arquivo de Códigos') then
begin
// a chave foi encontrada? vamos excluir
if reg.DeleteKey('Arquivo de Códigos') then
begin
ShowMessage('A chave foi excluída com sucesso.');
end
else
begin
ShowMessage('Não consegui excluir a chave especificada');
end;
end
else
begin
ShowMessage('A chave que você deseja excluir não foi encontrada.');
end;
// vamos liberar o registro
reg.Free;
end;
Note que este método remove a chave e todas as informações associadas a ela. Porém, se a chave possuir sub-chaves, estas deverão ser removidas individualmente antes de excluirmos a chave mãe. Para fins de compatibilidade, esta dica foi escrita usando Delphi 2009. |
Python ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em Python dados dois pontos no plano cartesianoQuantidade de visualizações: 3237 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem Python que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
# vamos importar o módulo Math
import math as math
def main():
# x e y do primeiro ponto
x1 = float(input("Coordenada x do primeiro ponto: "))
y1 = float(input("Coordenada y do primeiro ponto: "))
# x e y do segundo ponto
x2 = float(input("Coordenada x do segundo ponto: "))
y2 = float(input("Coordenada y do segundo ponto: "))
# agora vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1)
# e mostramos o resultado
print("O coeficiente angular é: %f\n\n" % m)
if __name__== "__main__":
main()
Ao executar este código em linguagem Python nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.666667 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
# vamos importar o módulo Math
import math as math
def main():
# x e y do primeiro ponto
x1 = float(input("Coordenada x do primeiro ponto: "))
y1 = float(input("Coordenada y do primeiro ponto: "))
# x e y do segundo ponto
x2 = float(input("Coordenada x do segundo ponto: "))
y2 = float(input("Coordenada y do segundo ponto: "))
# vamos obter o comprimento do cateto oposto
cateto_oposto = y2 - y1
# e agora o cateto adjascente
cateto_adjascente = x2 - x1
# vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
# (em radianos, não se esqueça)
tetha = math.atan2(cateto_oposto, cateto_adjascente)
# e finalmente usamos a tangente desse ângulo para calcular
# o coeficiente angular
tangente = math.tan(tetha)
# e mostramos o resultado
print("O coeficiente angular é: %f\n\n" % tangente)
if __name__== "__main__":
main()
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
C# ::: Threads ::: Thread |
Como usar a classe Thread para criar threads em seus programas C#Quantidade de visualizações: 12098 vezes |
A classe Thread permite criar e controlar uma thread, além de definir sua prioridade e obter seu status. Veja a posição desta classe na hierarquia de classes da plataforma .NET:
System.Object
System.Runtime.ConstrainedExecution.CriticalFinalizerObject
System.Threading.Thread
Um processo pode criar uma ou mais threads para executar parte do código do programa associado a tal processo. Usamos um delegate ThreadStart ou um delegate ParameterizedThreadStart para especificar o código do programa que será executado pela thread. O delegate ParameterizedThreadStart nos permite passar dados para as funções a serem executadas pela thread. Durante seu ciclo de vida, uma thread está sempre em um ou mais dos estados definidos pela enumeração ThreadState. Um nível de prioridade de agendamento, como definido na enumeração ThreadPriority, pode ser requisitado para a thread, mas, este comportamento nem sempre é garantido pelo sistema operacional. O método GetHashCode() fornece identificação para threads gerenciadas. Durante o ciclo de vida de uma thread, seu código de identificação não colidirá com os códigos das demais threads, independente do domínio da aplicação a partir do qual obtemos tal valor. Veja um trecho de código no qual criamos uma thread e a agendamos para execução paralela com a thread principal da aplicação. Note como os valores dos dois laços são exibidos de forma compartilhada pelas duas threads, ou seja, um thread exibe alguns valores e pára, para permitir que a outra faça parte do seu trabalho:
class Program{
static void Main(string[] args){
// using using System.Threading;
// vamos criar uma nova instância da clase Thread
// e fornecer o método que será executado
Thread thread = new Thread(contar);
// vamos agendar a thread para futura execução
thread.Start();
// agora vamos contar na thread principal
for (int i = 0; i <= 20; i++){
Console.Write("#" + Thread.CurrentThread.GetHashCode()
+ ": " + i + ", ");
}
Console.Write("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
// método que será chamado pela thread
static void contar(){
for (int i = 0; i <= 20; i++){
Console.Write("#" + Thread.CurrentThread.GetHashCode()
+ ": " + i + ", ");
}
}
}
Aqui eu usei a sintáxe de criação de objetos da classe Thread que cria uma instância de ThreadStart nos bastidores, ou seja, forneci apenas o método a ser executado pela nova thread. Note também que uma chamada ao método Start() da thread não faz com que a thread seja executada imediatamente. Este método apenas torna a thread elegível para execução, ou seja, no estado "pronta" (Running). É o sistema operacional que determina quando a mesma será executada. |
C ::: Dicas & Truques ::: Strings e Caracteres |
Como escrever uma função na linguagem C que verifica se duas strings são iguais ou diferentesQuantidade de visualizações: 9376 vezes |
|
Esta dica mostra como escrever uma função em C que verifica se duas strings são iguais ou diferentes. O nome da função é str_equal(). Esta função aceita duas strings como argumentos e retorna 1 se estas forem iguais e 0 em caso contrário. Experimente, faça as devidas alterações e adicione mais esta função ao seu repertório de códigos C. Veja o código completo para o exemplo:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// função personalizada que permite verificar
// se duas strings são iguais ou diferentes
int str_equal(const char *str1, const char *str2){
while((*str1 == *str2) && (*str1)){
str1++;
str2++;
}
return((*str1 == 0) && (*str2 == 0));
}
int main(int argc, char *argv[]){
char palavra1[] = "Java";
char palavra2[] = "Java";
if(str_equal(palavra1, palavra2) == 1)
printf("As palavras sao iguais");
else
printf("As palavras sao diferentes");
puts("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código nós teremos o seguinte resultado: As palavras são iguais |
Nossas 20 dicas & truques de programação mais populares |
|
Java - Como adicionar conteúdo a um arquivo texto existente em Java usando BufferedWriter e FileWriter JavaScript - Como filtrar os elementos de um array em JavaScript usando a função filter() - Vetores e matrizes em JavaScript C - Como comparar os primeiros n caracteres de duas strings usando a função strncmp() da linguagem C |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Python - Como usar a função type() da linguagem Python para descobrir o tipo de dados de uma variável JavaScript - Como remover todos os espaços de uma string em JavaScript usando uma função personalizada remover_espacos() |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





