C ::: Desafios e Lista de Exercícios Resolvidos ::: Engenharia Civil - Cálculo Estrutural

Exercícios Resolvidos de C - Como calcular as reações de apoio, momento de flexão máxima e forças cortantes em uma viga bi-apoiada com carga distribuída retangular usando C

Quantidade de visualizações: 1214 vezes
Pergunta/Tarefa:

Veja a seguinte figura: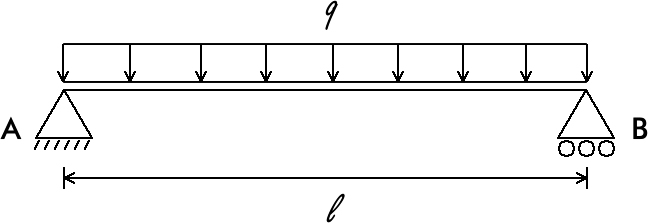



Nesta imagem temos uma viga bi apoiada com uma carga q distribuída de forma retangular a uma distância l. Para fins didáticos, vamos considerar que a carga q será em kN/m e a distância l será em metros. O apoio A é de segundo gênero e o apoio B é de primeiro gênero.

Escreva um programa C que solicita ao usuário que informe o valor da carga q e a distância l entre os apoios A e B. Em seguida mostre os valores das reações nos apoios A e B, o momento de flexão máxima da viga e o momento de flexão para uma determinada distância (que o usuário informará) a partir do apoio A.

Mostre também as forças cortantes nos apoios A e B. Lembre-se de que, para uma carga distribuída de forma retangular, o diagrama de momento fletor é uma parábola, enquanto o diagrama de cortante é uma reta (com o valor zero para a força cortante no meio da viga).

Sua saída deve ser parecida com:

Valor da carga em kN/m: 10
Distância em metros: 13

A reação no apoio A é: 65.000000 kN
A reação no apoio B é: 65.000000 kN
O momento fletor máximo é: 211.250000 kN

Informe uma distância a partir do apoio A: 4
O momento fletor na distância informada é: 180.000000 kN

A força cortante no apoio A é: 65.000000 kN
A força cortante no apoio B é: -65.000000 kN
Resposta/Solução:

Veja a resolução comentada deste exercício usando C:

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int main(int argc, char *argv[]) {
  // variáveis usadas na resolução do problema
  float carga, distancia, reacao_a, reacao_b;
  float flexao_maxima, distancia_temp, flexao_distancia;
  float cortante_a, cortante_b;
  
  // vamos pedir para o usuário informar o valor da carga
  printf("Valor da carga em kN/m: ");
  scanf("%f", &carga);
  
  // vamos pedir para o usuário informar a distância entre os apoios
  printf("Distancia em metros: ");
  scanf("%f", &distancia);
  
  // vamos calcular a reação no apoio A
  reacao_a = (1.0 / 2.0) * carga * distancia;
  
  // vamos calcular a reação no apoio B
  reacao_b = reacao_a;
  
  // vamos calcular o momento fletor máximo
  flexao_maxima = (1.0 / 8.0) * carga * pow(distancia, 2.0);
  
  // e mostramos o resultado
  printf("\nA reacao no apoio A e: %f kN", reacao_a);
  printf("\nA reacao no apoio B e: %f kN", reacao_b);
  printf("\nO momento fletor maximo e: %f kN", flexao_maxima);
  
  // vamos pedir para o usuário informar uma distância a
  // partir do apoio A
  printf("\n\nInforme uma distancia a partir do apoio A: ");
  scanf("%f", &distancia_temp);
  // vamos mostrar o momento fletor na distância informada
  if (distancia_temp > distancia) {
    printf("\nDistancia invalida.\n");
  }
  else {
    flexao_distancia = (1.0 / 2.0) * carga * distancia_temp * 
      (distancia - distancia_temp);
    printf("O momento fletor na distancia informada e: %f kN", 
      flexao_distancia);  
  }
  
  // vamos mostrar a força cortante no apoio A
  cortante_a = (1.0 / 2.0) * carga * distancia;
  printf("\n\nA forca cortante no apoio A e: %f kN", cortante_a);
  
  // vamos mostrar a força cortante no apoio B
  cortante_b = cortante_a * -1;
  printf("\nA forca cortante no apoio B e: %f kN\n\n", cortante_b);
  
  printf("\n\n");
  system("PAUSE");
  return 0;
}


Java ::: Dicas & Truques ::: Strings e Caracteres

Como retornar a representação numérica de um caractere em Java fazendo um cast de char para int

Quantidade de visualizações: 228 vezes
Um cast forçado de char para int é uma das formas mais práticas para se obter a representação numérica de um caractere em Java. Tudo que precisamos fazer é usar o método charAt() da classe String para obtermos o caractere na posição desejada de um texto, frase ou palavra e, em seguida, convertê-lo (cast) para um int.

Veja o código completo para o exemplo:

package arquivodecodigos;

// Este exemplo mostra como obter a representação
// númerica de um caractere

public class Estudos{
  public static void main(String[] args){
    String frase = "Programando em Java";
    
    for(int i = 0; i < frase.length(); i++){
      int valor = (int)frase.charAt(i);
      System.out.println(frase.charAt(i) + " = " 
        + valor);
    }    
        
    System.exit(0);
  }
}

Ao executar este código Java nós teremos o seguinte resultado:

P = 80
r = 114
o = 111
g = 103
r = 114
a = 97
m = 109
a = 97
n = 110
d = 100
o = 111
  = 32
e = 101
m = 109
  = 32
J = 74
a = 97
v = 118
a = 97


JavaScript ::: Dicas & Truques ::: Matemática e Estatística

Como elevar uma base a um determinado expoente usando o método pow() do objeto Math do JavaScript

Quantidade de visualizações: 24778 vezes
Em algumas situações nós precisamos efetuar cálculos de potenciação em JavaScript, ou seja, elevar um número (uma base) a um determinado expoente e obter sua potência. Veja a figura a seguir: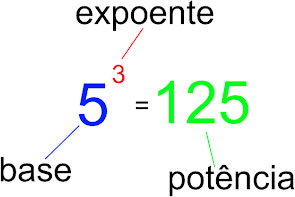



Veja que aqui o valor 5 foi elevado ao cubo, ou seja, ao expoente 3 e obtemos como resultado sua potência: 125.

A linguagem JavaScript nos fornece o método pow(), como parte do objeto Math, que recebe como argumentos a base e o expoente e nos retorna a potência. Veja um exemplo de seu uso no código abaixo:

<!doctype html>
<html>
<head>
 <title>Estudos JavaScript</title>
</head>
<body>

<script type="text/javascript">
  var base = 4;
  var expoente = 5;
  var potencia = Math.pow(4, 5);
  document.write("A base " + base + " elevada ao expoente "
    + expoente + " é igual à potência " + potencia);
</script>

</body>
</html>

Ao executarmos este código JavaScript nós teremos o seguinte resultado:

A base 4 elevada ao expoente 5 é igual a potencia 1024

Revit Python Shell ::: Dicas & Truques ::: Selection, Seleção

Como pedir para o usuário selecionar somente um elemento no Revit usando a função PickObject() do objeto Selection do Revit Python Shell

Quantidade de visualizações: 332 vezes
Nesta dica mostrarei como podemos usar a função PickObject() do objeto Selection do Revit Python Shell para pedir para o usuário selecionar somente um elemento na área de desenho do Revit. Note que o objeto Selection é obtido a partir do objeto uidoc, carregado automaticamente pelo Revit Python Shell.

Depois que o usuário seleciona o elemento, nós usamos a função doc.GetElement() para receber a referência ao elemento e convertê-la para um elemento real. Então, para finalizar, nós acessamos a propriedade Id do elemento e a exibimos na tela.

Veja o código Revit Python Shell completo para o exemplo: 

# faz o import necessário
from Autodesk.Revit.UI.Selection import ObjectType

# precisamos ocultar a janela do Revit Python Shell
__window__.Hide()
 
# agora fazemos uma chamada à função PickObject() do objeto Selection e retornamos
# uma Reference
selecionado = uidoc.Selection.PickObject(ObjectType.Element, "Selecione um elemento")
 
# depois que o usuário fizer a seleção nós mostramos a janela do
# Revit Python Shell novamente
__window__.Show()
__window__.Topmost = True
 
# obtemos o elemento a partir de sua referência usando a função
# GetElement() do objeto Document
elemento = doc.GetElement(selecionado)
 
# e mostramos o resultado
print("O id do elemento selecionado é: {0}".format(elemento.Id))

Ao executar este código Revit Python Shell nós teremos o seguinte resultado:

O id do elemento selecionado é: 359410

Veja como usei as funções __window__.Hide(), __window__.Show() e __window__.Topmost = True para ocultar a janela do Revit Python Shell e exibí-la novamente depois que o usuário fizer a seleção do elemento. Sem essas funções essa operação não pode ser realizada.

C++ ::: Dicas & Truques ::: Matemática e Estatística

Como calcular juros compostos e montante usando C++

Quantidade de visualizações: 17368 vezes
O regime de juros compostos é o mais comum no sistema financeiro e portanto, o mais útil para cálculos de problemas do dia-a-dia. Os juros gerados a cada período são incorporados ao principal para o cálculo dos juros do período seguinte.

Chamamos de capitalização o momento em que os juros são incorporados ao principal. Após três meses de capitalização, temos:

1º mês: M = P .(1 + i)
2º mês: o principal é igual ao montante do mês anterior: M = P x (1 + i) x (1 + i)
3º mês: o principal é igual ao montante do mês anterior: M = P x (1 + i) x (1 + i) x (1 + i)

Simplificando, obtemos a fórmula:

M = P . (1 + i)^n

Importante: a taxa i tem que ser expressa na mesma medida de tempo de n, ou seja, taxa de juros ao mês para n meses.

Para calcularmos apenas os juros basta diminuir o principal do montante ao final do período:

J = M - P

Vejamos um exemplo:

Considerando que uma pessoa empresta a outra a quantia de R$ 2.000,00, a juros compostos, pelo prazo de 3 meses, à taxa de 3% ao mês. Quanto deverá ser pago de juros?

Veja o código C++ para a resolução:

#include <iostream>

using namespace std;

int main(int argc, char *argv[])
{
  float principal = 2000.00;
  float taxa = 0.03; // 3%
  int meses = 3;
  
  float montante = principal * pow((1 + taxa), meses);
  float juros = montante - principal;
  
  cout << "O total de juros a ser pago é: " << 
      juros << "\n";
  cout << "O montante a ser pago é: " << 
      montante << "\n\n";
	
  system("PAUSE"); // pausa o programa
  return EXIT_SUCCESS;
}

Um outra aplicação interessante é mostrar mês a mês a evolução dos juros. Veja o código a seguir:

#include <iostream>

using namespace std;

int main(int argc, char *argv[])
{
  float principal = 2000.00;
  float taxa = 0.03; // 3%
  int meses = 3;
  float anterior = 0.0;
  float montante;
  float juros;
  
  for(int i = 1; i <= meses; i++){
    montante = principal * pow((1 + taxa), i);
    juros = montante - principal - anterior;
		
    anterior += juros;
  
    cout << "Mês: " << i << " - Montante: " <<
       montante << " - Juros " << juros << "\n";
  }
	
  system("PAUSE"); // pausa o programa
  return EXIT_SUCCESS;
}


Java ::: Classes e Componentes ::: JTable

Java Swing - Como obter a quantidade de colunas em uma JTable usando o método getColumnCount()

Quantidade de visualizações: 105 vezes
Nesta dica mostrarei como é possível contar as colunas de uma JTable com uma chamada ao método getColumnCount() da interface TableModel, que representa os dados contidos na tabela. Note que, neste exemplo, eu escrevi toda a aplicação Java Swing "na unha", ou seja, sem nenhum editor visual. Esta técnica é boa para entender todas as partes que compoem uma aplicação Java Swing.

Veja o código completo:

package arquivodecodigos;

import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
 
public class Estudos extends JFrame{
  public Estudos(){
    super("Exemplo de uma tabela simples");
         
    // colunas da tabela
    String[] colunas = {"Cidade", "Estado", "Habitantes"};
         
    // conteúdo da tabela
         
    Object[][] conteudo = {
        {"Goiânia", "GO", "43.023.432"},
        {"São Paulo", "SP", "5.343.234"},
        {"Rio de Janeiro", "RJ", "6.434.212"},
        {"Jussara", "GO", "87.454"},
        {"Barra do Garças", "MT", "64.344"}
    };
         
    // constrói a tabela
    final JTable tabela = new JTable(conteudo, colunas);
    tabela.setPreferredScrollableViewportSize(
      new Dimension(350, 50));
     
    Container c = getContentPane();
    c.setLayout(new FlowLayout());
         
    JButton btn = new JButton("Número de Colunas");
    btn.addActionListener(
      new ActionListener(){
        public void actionPerformed(ActionEvent e){
          JOptionPane.showMessageDialog(null,
            "Quantidade de colunas: " + 
            tabela.getModel().getColumnCount(), 
            "JTable", JOptionPane.INFORMATION_MESSAGE);  
        }
      }
    );
         
    JScrollPane scrollPane = new JScrollPane(tabela);
    c.add(scrollPane);
    c.add(btn);
         
    setSize(400, 300);
    setVisible(true);
  }
     
  public static void main(String args[]){
    Estudos app = new Estudos();
    app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
  }
}

Ao executar este exemplo e clicar no botão nós veremos uma mensagem JOptionPane.showMessageDialog() com o seguinte texto:

Quantidade de colunas: 3

Java ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas

Como calcular o diâmetro, a circunferência e a área de um círculo dado o raio em Java - Java para Geometria

Quantidade de visualizações: 2415 vezes
O círculo é uma figura geométrica plana e que possui quatro características: seu raio, seu diâmetro, sua circunferência e sua área. Aqui já podemos aproveitar e relembrar a diferença entre o círculo e a circunferência. O círculo é o conjunto de pontos resultantes da união entre uma circunferência e seus pontos internos, ou seja, o círculo é a área cuja delimitação é uma circunferência.

É importante observar que alguns autores tratam o círculo como uma circunferência. Assim, para estes autores, calcular a circunferência de um círculo equivale a calcular o perímetro da circunferência.

Veja a figura a seguir para relembrar o que é o raio de um círculo:



Nesta dica mostrarei como podemos usar Java para calcular o diâmetro, a circunferência e a área de um círculo tendo apenas o raio como informação. Antes, porém, vamos às formulas. Sabendo que r é o raio, temos:

\[\text{Diâmetro d} = 2 \times r \]

\[\text{Circunferência C} = 2 \times \pi \times r \]

\[\text{Área A} = \pi \times r^2 \]

Agora vamos ver o código Java que solicita ao usuário que informe o raio do círculo e mostra o diâmetro, a circunferência e a área:

package arquivodecodigos;

import java.util.Scanner;

public class Estudos{
  public static void main(String[] args){
    Scanner entrada = new Scanner(System.in);
    
    // vamos ler o raio do círculo
    System.out.print("Informe o raio do círculo: ");
    double raio = Double.parseDouble(entrada.nextLine());
    
    // vamos achar o diâmetro do círculo
    double diametro = 2 * raio;
    // agora calculamos a circunferência
    double circunferencia = 2 * Math.PI * raio;
    // finalmente calculamos a área do círculo
    double area = Math.PI * Math.pow(raio, 2);
    
    // vamos mostrar os resultados
    System.out.println("O diâmetro do círculo é: " +
      diametro);
    System.out.println("A circunferência do círculo é: " +
      circunferencia);
    System.out.println("A área do círculo é: " + area);
  }
}

Ao executar este código Java nós teremos o seguinte resultado:

Informe o raio do círculo: 10
O diâmetro do círculo é: 20.0
A circunferência do círculo é: 62.83185307179586
A área do círculo é: 314.1592653589793

Lembre-se de que a área é em centímetros quadrados, metros quadrados, etc.

Java ::: Dicas & Truques ::: Arquivos e Diretórios

Como criar diretórios em Java usando o método mkdir() da classe File

Quantidade de visualizações: 174 vezes
Em algumas ocasiões nossos programas precisam criar diretórios. Na linguagem Java isso pode ser feito com o auxílio do método mkdir() da classe File, do pacote java.io.

Este método não recebe nenhum parâmetro e atua em cima de uma instância da classe File. Além disso, ele retorna um boolean indicando o sucesso ou não da operação.

Veja o código completo para um exemplo: 

package arquivodecodigos;

// precisamos importar o pacote java.io
import java.io.*;
 
public class Estudos{
  public static void main(String[] args){
    // nome e caminho do diretório que será criado
    File diretorio = new File("c:\\estudos_java\\imagens");
         
    // o diretório foi criado com sucesso?
    if(diretorio.mkdir()){
      System.out.println("Diretório criado com sucesso");
    }
    else{
      System.out.println("Nao foi possível criar o diretório");
    }
  }
}

Se o diretório puder ser criado, você verá uma mensagem:

Diretório criado com sucesso

Observe que este método pode disparar uma exceção do tipo SecurityException se você não tiver permissão para criar diretórios nos locais especificados.

Python ::: Python para Engenharia ::: Engenharia Civil - Cálculo Estrutural

Como calcular a Posição da Linha Neutra em vigas de concreto armado usando Python - Python para Engenharia Civil - Cálculo Estrutural

Quantidade de visualizações: 218 vezes
O concreto possui excelente resistência à compressão, porém, sua resistência à tração é muito pequena, chegando em torno de 10% da sua resistência à compressão. O aço, por sua vez, apresenta alta resistência à tração.

Por esta razão a combinação destes dois materiais resulta no que conhecemos por concreto armado, no qual o concreto, no caso das vigas, resiste às solicitações de compressão (em geral na parte superior da viga) e o aço se encarrega da tração (na parte inferior da viga).

Entre as forças de compressão e tração da viga de concreto armado existe uma região na qual as tensões são nulas, ou seja, não há nem tração nem compressão. Essa região é conhecida como linha neutra da viga e é usada, entre outras coisas, para verificarmos se a viga se encontra nas condições mínimas de dutibilidade exigidas pela ABNT NBR 6118/2014.

Outra característica muito importante da linha neutra é que ela nos permite indicar em qual domínio de deformação as nossas vigas de concreto armado estão trabalhando.

A posição da linha neutra em vigas de concreto armado pode ser calculada por meio da seguinte fórmula:

\[x = 1,25 \cdot d \cdot \left(1 - \sqrt{1 - \frac{M_d}{0,425 \cdot b_w \cdot d^2 \cdot f_\text{cd}}}\right)\]

Onde:

x é a posição da linha neutra a partir da fibra mais comprimida da viga, em metros (que depois convertemos para cm);

d é a altura útil da viga em metros;

Md é o momento solicitante de cálculo na viga, em kN.m;

bw é a largura da viga, em metros;

fcd é a resistência de cálculo do concreto, em kN/m2;

Veja agora o código Python completo que pede para o usuário informar a altura e largura da viga em centímetros, o momento solicitante na viga em kN.m e o FCK do concreto em Mpa, mostra a posição da linha neutra da viga e informa se ela obedece ao valor máximo imposto pela ABNT NBR 6118/2014 e também o domínio de deformação que ela está atuando:

# precisamos importar o módulo Math
import math

# função principal do programa Python
def main():
  # vamos pedir para o usuário informar a altura da viga
  altura = float(input("Informe a altura H da viga em cm: "))
  # vamos converter de centímetros para metros
  altura = altura / 100.00

  # vamos pedir para o usuário informar a largura da viga
  largura = float(input("Informe a largura bw da viga em cm: "))
  # vamos converter de centímetros para metros
  largura = largura / 100.00

  # vamos calcular a altura útil da viga
  # aqui eu usei 0.9 mas alguns engenheiros usam 0.95
  altura_util = 0.9 * altura

  # vamos pedir para o usuário informar o momento
  # máximo solicitante Mk (calculado no Ftool ou outra ferramenta)
  Mk = float(input("Informe o momento solicitante Mk em kN.m: "))
  # vamos definir o valor do gama f
  yf = 1.4
  # calculamos o md, ou seja, o momento solicitante de cálculo
  Md = Mk * yf

  # vamos pedir para o usuário informar o FCK do concreto
  fck = float(input("Informe o FCK do concreto em Mpa: "))
  # vamos definir o valor do gama c
  yc = 1.4
  # calculamos o fcd, ou seja, a resistência de cálculo do concreto
  fcd = fck / yc

  # finalmente vamos calcular a posição da linha neutra
  # note que converti o fcd de Mpa para kN/m2
  x = 1.25 * altura_util * (1 - math.sqrt(1 - (Md / (0.425 *
    largura * math.pow(altura_util, 2) * (fcd * 1000.0)))))
  
  # vamos mostrar os resultados 
  print("\nA altura útil da viga é: {0} cm ({1} m)".format(
    round(altura_util * 100, 5), round(altura_util, 5)))
  print("O momento solicitante de cálculo é: {0} kN.m".format(
    round(Md, 5)))
  print("O fcd do concreto é: {0} Mpa".format(round(fcd, 5)))
  print("A posição da linha neutra é: {0} cm".format(round(x * 100.0, 5)))
  
  # vamos verificar se a posição da linha neutra está dentro do
  # limite máximo imposto pela ABNT NBR 6118/2014 para FCK até 50 Mpa
  if ((x / altura_util) <= 0.45):
    print("Garante condições mínimas de dutibilidade? SIM")
  else:
    print("Garante condições mínimas de dutibilidade? NÃO")

  # vamos verificar o domínio de deformação da vaga
  temp = x / altura_util
  if (temp <= 0.167):
    print("A viga está trabalhando no domínio 1")
  elif ((temp > 0.167) and (temp <= 0.259)):
    print("A viga está trabalhando no domínio 2")
  elif ((temp > 0.259) and (temp <= 0.628)):
    print("A viga está trabalhando no domínio 3")
  else:
    print("A viga está trabalhando no domínio 4/5")

if __name__ == "__main__":
  main()

Ao executar este código Python nós teremos o seguinte resultado:

Informe a altura H da viga em cm: 35
Informe a largura bw da viga em cm: 19
Informe o momento solicitante Mk em kN.m: 32.3
Informe o FCK do concreto em Mpa: 25

A altura útil da viga é: 31.5 cm (0.315 m)
O momento solicitante de cálculo é: 45.22 kN.m
O fcd do concreto é: 17.85714 Mpa
A posição da linha neutra é: 6.81136 cm
Garante condições mínimas de dutibilidade? SIM
A viga está trabalhando no domínio 2

Python ::: Dicas & Truques ::: Data e Hora

Datas e horas em Python - Como obter o nome do dia da semana no formato longo (segunda-feira, terça-feira, etc) usando a função strftime() do Python

Quantidade de visualizações: 8945 vezes
Nesta dica eu mostro como podemos usar a função strftime() da linguagem Python para obter e exibir o nome do dia da semana no formato longo e em português, ou seja, segunda-feira, terça-feira, quarta-feira, etc.

Veja o código completo para o exemplo:

from datetime import datetime
import locale

# função principal do programa
def main():
  # Configurações do usuário
  locale.setlocale(locale.LC_ALL, '')
 
  # Obtém um datatime da data e hora atual
  hoje = datetime.today()
 
  # Exibe o nome do dia da semana no formato
  # longo
  print("O dia da semana é:", hoje.strftime("%A"))
 
if __name__== "__main__":
  main()

Ao executarmos este código nós teremos o seguinte resultado:

O dia da semana é: quinta-feira

Carregar Publicações Anteriores

Nossas 20 dicas & truques de programação mais populares

Você também poderá gostar das dicas e truques de programação abaixo

Nossas 20 dicas & truques de programação mais recentes

Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site

Últimos Exercícios Resolvidos

E-Books em PDF
E-Book 350 Exercícios Resolvidos de Java - PDF com 500 páginas
Domine lógica de programação e a linguagem Java com o nosso E-Book 350 Exercícios Exercícios de Java, para você estudar onde e quando quiser.

Este e-book contém exercícios resolvidos abrangendo os tópicos: Java básico, matemática e estatística, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.
Ver Conteúdo do E-book
E-Book 650 Dicas, Truques e Exercícios Resolvidos de Python - PDF com 1.200 páginas
Domine lógica de programação e a linguagem Python com o nosso E-Book 650 Dicas, Truques e Exercícios Exercícios de Python, para você estudar onde e quando quiser.

Este e-book contém dicas, truques e exercícios resolvidos abrangendo os tópicos: Python básico, matemática e estatística, banco de dados, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.
Ver Conteúdo do E-book

Linguagens Mais Populares

1º lugar: Java
2º lugar: Python
3º lugar: C#
4º lugar: PHP
5º lugar: C
6º lugar: Delphi
7º lugar: JavaScript
8º lugar: C++
9º lugar: VB.NET
10º lugar: Ruby
Questões de Concurso para Engenharia Civil
Fundações
Instalações Hidráulicas Prediais
Fenômenos de Transporte e Hidráulica
Estruturas de Aço e Madeira
Exercícios Resolvidos
Lista de Exercícios Resolvidos de Java
Lista de Exercícios Resolvidos de C
Lista de Exercícios Resolvidos de C++
Bancos de Dados
MySQL
Firebird
MS SQL Server
PostgreSQL
Questões de Concurso
Topografia
Hidrologia
Hidrostática
Ética e Legislação Profissional
Frameworks
jQuery
AngularJS
React / ReactJS / React.js
Laravel
Projetos e Códigos Fonte
Projetos e Códigos Fonte Java
Projetos e Códigos Fonte PHP
Projetos e Códigos Fonte Python
Especializações
Data Science
Calculadoras
Calculadoras de Topografia
Calculadoras de Matemática
Calculadoras de Data e Hora
Calculadoras de Física
Calculadoras de Estatística
Calculadoras de Trigonometria
Calculadoras de Matrizes
Calculadoras de Vetores
Ferramentas
Tabela de Cores Flat Design
Tabela de Cores do Material Design do Google
Tabela de Cores Web Safe Colors
Todas as Linguagens, Frameworks, Biliotecas e Bancos de Dados
.NET Framework | ActionScript | Adobe AIR | Adobe Flex | AJAX | Android Java | Angular | AngularJS | Apache Ant | Apache Maven | Apache Tomcat | Apache Web Server | Arduino | ASP.NET | AutoCAD | AutoCAD .NET API C# | AutoCAD Civil 3D | AutoCAD Civil 3D .NET C# | AutoCAD VBA | AutoLISP | Bourne Again Shell (bash Shell) | C | C# | C++ | C++ Builder | CodeIgniter | CSS | Dart | Data Science | Delphi | DHTML (Dynamic HTML) | Django | Eclipse IDE | Elixir | Enterprise JavaBeans (EJB) | Erlang | Excel | Excel VBA | Ext JS | Facelets | Firebird | Flutter | Fórmulas da Física | Geral | GNU Octave | GoLang | Groovy | GTK+ | Haskell | HEC-RAS | Hibernate | HTML/XHTML | HTML5 | IBM DB2 | iReport | iTextSharp | Java | Java Servlets | JavaFX | JavaScript | JBoss | JPA - Java Persistence Architecture API - Arquitetura de Persistência Java | jQuery | jQuery UI | JSF - Java Server Faces | JSP (Java Server Pages) | Kotlin | Laravel | Linux | LISP | MongoDB | MS SQL Server | MySQL | NetBeans IDE | NetBeans IDE | Node.js | Perl | PHP | PHP-GTK | Portugol | PostgreSQL | Processing.py | Python | QGIS | Qt | R | React | React Native | React.js | Revit C# | Revit Python Shell | Ruby | Ruby On Rails | Rust | Smarty | Struts | Struts 2 | Tcl e Tcl/Tk | TypeScript | VB.NET | VBA | Visual LISP | VisuAlg | WebGL (Web Graphics Library) | wxWidgets | Zend Framework |

© 2025 Arquivo de Códigos - Todos os direitos reservados
Neste momento há 36 usuários muito felizes estudando em nosso site.