CSS ::: Dicas & Truques ::: Barras de Navegação, Menus e Dropdowns |
Como criar uma barra de menus na horizontal usando CSS e o valor inline-block para a propriedade displayQuantidade de visualizações: 566 vezes |
|
Nesta dica mostrarei como podemos criar uma barra de menus horizontal usando CSS. Para isso cada item de menu será um elemento <li>, contidos dentro de um elemento <ul>. O truque é definir o valor inline-block para a propriedade display de cada elemento <li>. Veja a página HTML e CSS completa para o exemplo:
<!doctype html>
<html>
<head>
<title>Estudos CSS</title>
<style>
#menu{
background-color: #eeeeee;
list-style-type: none;
text-align: center;
margin: 0;
padding: 0;
}
#menu li {
display: inline-block;
font-size: 20px;
padding: 20px;
text-decoration: none;
}
#menu li a{
text-decoration: none;
}
</style>
</head>
<body>
<h1>Exemplo de Barra de Menu Horizontal</h1>
<p>Veja como podemos usar o valor inline-block para
a propriedade display do CSS para criar uma barra
de menu na horizontal</p>
<ul id="menu">
<li><a href="index.php">Início</a></li>
<li><a href="servicos.php">Serviços</a></li>
<li><a href="produtos.php">Produtos</a></li>
<li><a href="contatos.php">Contatos</a></li>
</ul>
</body>
</html>
|
JavaScript ::: Dicas & Truques ::: Data e Hora |
Como usar o objeto Date em JavaScript - Curso de JavaScript para iniciantesQuantidade de visualizações: 7445 vezes |
O objeto Date é um tipo de dados embutido na linguagem JavaScript. Objetos Date são criados, em sua forma mais simples (construtor sem argumentos), da seguinte forma:
<html>
<head>
<title>Estudos JavaScript</title>
</head>
<body>
<script type="text/javascript">
// vamos criar um novo objeto Date
var hoje = new Date();
// vamos exibir a representação deste objeto Date
document.write("Data e hora atual: " + hoje);
</script>
</body>
</html>
Ao executarmos este código teremos um resultado parecido com: Data e hora atual: Fri Mar 18 10:02:02 UTC-0300 2011 Note que a representação textual de um objeto Date é a data atual no formato curto (em inglês), as horas e a diferença em relação ao horário UTC (Universal Time Coordinated, sucessor do GMT - Greenwich Mean Time). Uma vez criado um objeto Date, podemos usar vários de seus métodos para operar sobre seus valores de datas e horas. A maioria dos métodos serve simplesmente para obter ou definir os valores dos campos ano, mês, dia, horas, minutos, segundos e milisegundos, usando a hora local ou UTC. O método toString() e suas variantes nos permitem converter datas e horas para os formatos comumente exibidos aos usuários. Veja um exemplo:
<script type="text/javascript">
// vamos criar um novo objeto Date
var hoje = new Date();
// vamos exibir a representação deste objeto Date
document.write("Data e hora atual: " + hoje.toLocaleString());
</script>
Ao executarmos este código teremos um resultado parecido com: Data e hora atual: sexta-feira, 18 de março de 2011 15:44:07 Aqui nós usamos o método toLocaleString() do objeto Date para exibir a data e hora de acordo com as configurações regionais do computador local. Os métodos getTime() e setTime() obtém ou definem a representação interna do objeto Date como o número de milisegundos decorridos desde a meia-noite do dia 1º de janeiro de 1970 (GMT). Neste formato padrão de milisegundos, a data e hora são representadas por um único inteiro, o que facilita os cálculos envolvendo datas e horas. O padrão ECMAScript exige que o objeto Date seja capaz de representar qualquer data e hora, na precisão de milisegundos, na faixa de 100 milhões de anos antes ou depois de 01/01/1970. |
Delphi ::: Data Access Controls (Controles de Acesso a Dados) ::: TField e Classes Derivadas |
Como usar a classe TField em seus programas DelphiQuantidade de visualizações: 12574 vezes |
|
A classe TField (na unit DB) é um ancestral comum de todos os componentes que representam os campos de uma tabela no banco de dados (ou um dataset cujos dados foram carregados de um arquivo do tipo texto, binário ou XML). Esta classe encapsula o comportamento comum a todos os demais componentes to tipo field (campo). Veja sua posição na hierarquia de classes do Delphi:
System.TObject
Classes.TPersistent
Classes.TComponent
DB.TField
A classe TField apresenta propriedades, eventos e métodos que são usados para as seguintes tarefas: 1) Alterar o valor de um campo em um dataset; 2) Converter o valor de um campo de um tipo para outro tipo; 3) Efetuar validações nos dados informados pelos usuários para determinados campos; 4) Definir como as informações dos campos são mostradas em tempo de exibição ou para edição; 5) Calcular o valor de um campo a partir de código escrito no evento OnCalcFields do dataset; 6) Pesquisar o valor do campo a partir de outro dataset. Em geral não criamos instâncias da classe TField diretamente. Componentes que descendem de TField são criados automaticamente a cada vez que o dataset é ativado. Estes descendentes podem ser dinâmicos (o padrão) ou persistentes. Componentes campos dinâmicos refletem as colunas dos metadados da tabela a qual pertencem no momento que o dataset é aberto. Componentes campos persistentes são criados em tempo de design usando o editor Fields, que especifica os campos no dataset, suas propriedades e a ordem em que deverão estar. A criação de componentes de campos persistentes garante que todas as vezes que uma aplicação for executada, ela usará e exibirá as mesmas colunas, na mesma ordem, até mesmo se a estrutura física da base de dados mudar. Se uma coluna em uma tabela na qual um componente de campo persistente é baseado for excluída ou alterada, o IDE gera uma exceção em vez de permitir a abertura do dataset usando um coluna não existente ou incompatível. Se isso acontecer, devemos remover o camponente field para o campo não existente usando o editor Fields. Um campo (field) em um dataset é sempre tratado como uma das classes descendentes de TField abaixo: TADTField TDateField TReferenceField TAggregateField TDateTimeField TSmallIntField TArrayField TFloatField TSQLTimeStampField TAutoIncField TFMTBCDField TStringField TBCDField TGraphicField TTimeField TBinaryField TGuidField TVarBytesField TBlobField TIDispatchField TVariantField TBooleanField TIntegerField TWideStringField TBytesField TInterfaceField TWordField TCurrencyField TLargeintField TDataSetField TMemoField
procedure TForm3.Button3Click(Sender: TObject);
var
campo: TField;
begin
// vamos obter o campo com o nome "titulo" do registro atual
campo := ClientDataSet1.FieldByName('titulo');
// vamos mostrar o valor do campo
ShowMessage('O valor do campo é: ' + campo.AsString);
end;
Ao executarmos este código teremos um resultado parecido com: "O valor do campo é: Programando em Java". Esta dica foi escrita e testada no Delphi 2009. |
Java ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a equação reduzida da reta em Java dados dois pontos pertencentes à retaQuantidade de visualizações: 1386 vezes |
|
Nesta dica de Java veremos como calcular a equação reduzida da reta quando temos dois pontos pertencentes à esta reta. Não, nessa dica não vamos calcular a equação geral da reta, apenas a equação reduzida. Em outras dicas do site você encontra como como isso pode ser feito. Para relembrar: a equação reduzida da reta é y = mx + n, em que x e y são, respectivamente, a variável independente e a variável dependente; m é o coeficiente angular, e n é o coeficiente linear. Além disso, m e n são números reais. Com a equação reduzida da reta, é possível calcular quais são os pontos que pertencem a essa reta e quais não pertencem. Vamos começar então analisando a seguinte figura, na qual temos dois pontos que pertencem à uma reta: 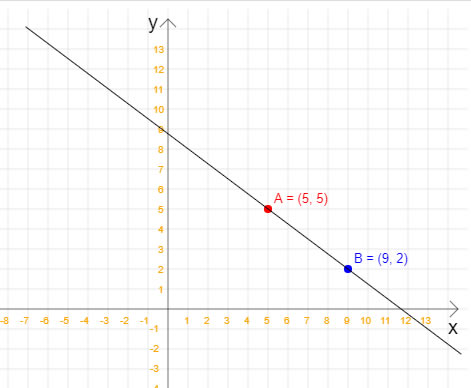 Note que a reta da figura passa pelos pontos A(5, 5) e B(9, 2). Então, uma vez que já temos os dois pontos, já podemos calcular a equação reduzida da reta. Veja o código Java completo para esta tarefa:
package estudos;
import java.util.Scanner;
public class Estudos{
public static void main(String[] args){
// vamos usar a classe Scanner para ler os dados
Scanner entrada = new Scanner(System.in);
// vamos ler as coordenadas do primeiro ponto
System.out.print("Coordenada x do primeiro ponto: ");
double x1 = Double.parseDouble(entrada.nextLine());
System.out.print("Coordenada y do primeiro ponto: ");
double y1 = Double.parseDouble(entrada.nextLine());
// vamos ler as coordenadas do segundo ponto
System.out.print("Coordenada x do segundo ponto: ");
double x2 = Double.parseDouble(entrada.nextLine());
System.out.print("Coordenada y do segundo ponto: ");
double y2 = Double.parseDouble(entrada.nextLine());
String sinal = "+";
// vamos calcular o coeficiente angular da reta
double m = (y2 - y1) / (x2 - x1);
// vamos calcular o coeficiente linear
double n = y1 - (m * x1);
// coeficiente linear menor que zero? O sinal será negativo
if (n < 0){
sinal = "-";
n = n * -1;
}
// mostra a equação reduzida da reta
System.out.println("Equação reduzida: y = " + m + "x"
+ " " + sinal + " " + n);
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 5 Coordenada y do primeiro ponto: 5 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 2 Equação reduzida: y = -0,75x + 8,75 Para testarmos se nossa equação reduzida da reta está realmente correta, considere o valor 3 para o eixo x da imagem acima. Ao efetuarmos o cálculo: >> y = (-0.75 * 3) + 8.75 y = 6.5000 temos o valor 6.5 para o eixo y, o que faz com que o novo ponto caia exatamente em cima da reta considerada na imagem. |
Python ::: Python para Engenharia ::: Engenharia Civil - Cálculo Estrutural |
Como calcular o Índice de Esbeltez de um pilar em Python - Python para Engenharia Civil e Cálculo EstruturalQuantidade de visualizações: 339 vezes |
 O índice de esbeltez de um pilar, representado pela letra grega λ (lambda) é uma relação que mede a altura do pilar em relação à sua largura ou seção transversal. Esse índice é usado para avaliar a suscetibilidade de um pilar à flambagem, que é um tipo de falha estrutural que pode ocorrer em pilares esbeltos sob compressão. Segundo a NBR 6118, 15.8.2, os pilares devem ter índice de esbeltez menor ou igual a 200 (λ ≤ 200). Apenas no caso de postes com força normal menor que 0,10 fcd x Ac, o índice de esbeltez pode ser maior que 200. O índice de esbeltez é a razão entre o comprimento de flambagem e o raio de giração, nas direções a serem consideradas. De acordo com o comprimento de flambagem, os pilares classificam-se como: curto, se λ < 35; medianamente esbelto, se 35 < λ < 90; esbelto, se 90 < λ < 140; e muito esbelto, se 140 < λ < 200. A fórmula para o cálculo do índice de esbeltez pode ser definida como: \[\lambda = 3,46 \cdot \frac{le}{h} \] Onde: λ = número adimensional representando o índice de esbeltez ao longo da direção escolhida (x ou y); le = algura do pilar, ou seja, o comprimento do pilar em centímetros. h = dimensão escolhida (x ou y) em centímetros. De acordo com a norma NBR 6118 (ABNT, 2014), se o índice de esbeltez na direção escolhida for menor que 35, nós não precisamos considerar os efeitos locais de 2ª ordem. Vamos agora ao código Python? Pediremos ao usuário para informar o comprimento (altura) do pilar em metros, as dimensões nas direções x e y e mostraremos os índices de esbeltez nas direções x e y do pilar com as respectivas anotações da necessidade ou não da consideração dos efeitos locais de 2ª ordem. Veja:
# método principal
def main():
# vamos pedir o comprimento do pilar em metros (pé direito)
le = float(input("Informe o comprimento do pilar (em metros): "))
# vamos converter o comprimento em metros para centímetros
le = le * 100.0
# vamos pedir as dimensões do pilar
hx = float(input("Informe a dimensão do pilar na direção x (em cm): "))
hy = float(input("Informe a dimensão do pilar na direção y (em cm): "))
# agora vamos calcular o índice de esbeltez na direção x
lambda_x = 3.46 * (le / hx)
# agora vamos calcular o índice de esbeltez na direção y
lambda_y = 3.46 * (le / hy)
# e mostramos os resultados
print("\nO índice de esbeltez na direção x é: {0}".format(round(lambda_x, 2)))
# precisamos considerar os efeitos locais de segunda ordem na direção x?
if lambda_x < 35:
print("Não considerar os efeitos locais de 2ª ordem na direção x")
else:
print("Considerar os efeitos locais de 2º ordem na direção x")
print("\nO índice de esbeltez na direção y é: {0}".format(round(lambda_y, 2)))
# precisamos considerar os efeitos locais de segunda ordem na direção y?
if lambda_y < 35:
print("Não considerar os efeitos locais de 2ª ordem na direção y")
else:
print("Considerar os efeitos locais de 2ª ordem na direção y")
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Informe o comprimento do pilar (em metros): 2.88 Informe a dimensão do pilar na direção x (em cm): 40 Informe a dimensão do pilar na direção y (em cm): 19 O índice de esbeltez na direção x é: 24.91 Não considerar os efeitos locais de 2ª ordem na direção x O índice de esbeltez na direção y é: 52.45 Considerar os efeitos locais de 2ª ordem na direção y |
Java ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como converter um vetor (array) em uma List usando o método asList() da classe Arrays da linguagem JavaQuantidade de visualizações: 15063 vezes |
|
Em algumas situações nós gostaríamos de obter uma List, ou melhor, um objeto da interface List, a partir de um vetor (um array). Nesta dica mostrarei como isso é possível. Nós vamos criar um vetor de cinco objetos da classe Integer, vamos instanciar estes objetos com valores inteiros e, em seguida, vamos obter um objeto List contendo os mesmos. Veja o código completo para o exemplo:
package arquivodecodigos;
import java.util.*;
public class Estudos{
public static void main(String[] args){
Integer[] valores = new Integer[5];
// inicializa os elementos do array
valores[0] = 1;
valores[1] = 2;
valores[2] = 3;
valores[3] = 4;
valores[4] = 5;
List lista = Arrays.asList(valores);
// percorre a lista
for(int i = 0; i < lista.size(); i++){
Integer valor = (Integer)(lista.get(i));
System.out.println(valor.toString());
}
System.exit(0);
}
}
Ao executar este código nós teremos o seguinte resultado: 1 2 3 4 5 |
Ruby ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de Ruby - Escreva um programa Ruby para mover todos os zeros para o final do vetor, sem alterar a ordem dos elementos já presentes no arrayQuantidade de visualizações: 1226 vezes |
|
Pergunta/Tarefa: Dado o seguinte vetor de inteiros: # vamos declarar e construir um vetor de 8 inteiros valores = [0, 3, 0, 5, 7, 4, 0, 9] Sua saída deverá ser parecida com: Vetor na ordem original: 0 3 0 5 7 4 0 9 Vetor com os zeros deslocados para o final: 3 5 7 4 9 0 0 0 Veja a resolução comentada deste exercício usando Ruby:
# vamos declarar e construir um vetor de 8 inteiros
valores = [0, 3, 0, 5, 7, 4, 0, 9]
# vamos mostrar o vetor na ordem original
print("Vetor na ordem original:\n")
for i in (0..valores.length - 1)
printf("%d ", valores[i])
end
# vamos inicializar j como 0 para que ele aponte para
# o primeiro elemento do vetor
j = 0
# agora o laço for percorre todos os elementos do vetor,
# incrementanto a variável i e deixando o j em 0
for i in (0..valores.length - 1)
# encontramos um valor que não é 0
if(valores[i] != 0)
# fazemos a troca entre os elementos nos índices
# i e j
temp = valores[i]
valores[i] = valores[j]
valores[j] = temp
# e avançamos o j para o elemento seguinte
j = j + 1
end
end
# agora mostramos o resultado
print("\n\nVetor com os zeros deslocados para o final:\n")
for i in (0..valores.length - 1)
printf("%d ", valores[i])
end
Não se esqueça: A resolução do exercício deve ser feita sem a criação de um vetor, array ou lista adicional, e os elementos diferentes de zero devem permanecer na mesma ordem que eles estavam antes. |
Ruby ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como adicionar itens ao final de um array em Ruby usando o operador <<Quantidade de visualizações: 6592 vezes |
|
Nesta dica mostrarei como podemos usar o operador << da linguagem Ruby para adicionar novos elementos no final de um array. Veja o código completo para o exemplo:
# vamos criar um array de nomes
nomes = []
# Lê entrada até que o valor -1 seja
# fornecido
loop do
print "Digite um nome (-1 para sair): "
nome = gets.chomp
# vamos adicionar este nome no final do
# array
if nome != "-1"
nomes << nome # adiciona o nome ao array
end
# vamos sair do laço se o valor for "-1"
if nome == "-1"
break
end
end
# Exibe todos os valores do array
puts "\nOs nomes fornecidos foram:"
nomes.each do | nome |
puts nome
end
Ao executar este código Ruby nós teremos o seguinte resultado: Digite um nome (-1 para sair): FERNANDA Digite um nome (-1 para sair): LAURA Digite um nome (-1 para sair): ISADORA Digite um nome (-1 para sair): CINTIA Digite um nome (-1 para sair): -1 Os nomes fornecidos foram: FERNANDA LAURA ISADORA CINTIA |
C# ::: Windows Forms ::: ComboBox |
Como excluir todos os itens de um ComboBox do C# Windows Forms usando a função Clear() da classe ComboBox.ObjectCollectionQuantidade de visualizações: 10084 vezes |
Há algumas situações nas quais precisamos remover (limpar) todos os itens de um ComboBox. Isso pode ser feito com uma chamada ao método Clear() da classe ComboBox.ObjectCollection. Temos acesso a esta classe por meio da propriedade Items da classe ComboBox. Vja o exemplo:
private void button1_Click(object sender, EventArgs e){
// exclui todos os itens do ComboBox chamado
// linguagensCombo
linguagensCombo.Items.Clear();
}
|
VB.NET ::: Dicas & Truques ::: Strings e Caracteres |
Como inverter uma string em VB.NET usando a função StrReverse()Quantidade de visualizações: 10870 vezes |
|
Em algumas situações nós precisamos inverter a ordem dos caracteres de uma palavra, frase ou texto em VB.NET. Para isso nós podemos usar a função StrReverse(). Veja um exemplo completo de seu uso:
Imports System
Module Program
Sub Main(args As String())
Dim frase As String = "Gosto de VB.NET"
' vamos mostrar a frase original
Console.WriteLine("A frase original é: " & frase)
' vamos inverter a string
frase = StrReverse(frase)
' mostramos a frase invertida
Console.WriteLine("A frase invertida é: " & frase)
Console.WriteLine(vbCrLf & "Pressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código VB.NET nós teremos o seguinte resultado: A frase original é: Gosto de VB.NET A frase invertida é: TEN.BV ed otsoG |
Nossas 20 dicas & truques de programação mais populares |
|
AutoLISP - Como retornar o nome da layer atual do AutoCAD usando AutoLISP e a variável de sistema CLAYER PHP - Programação Orientada a Objetos em PHP - Aprenda a criar e usar métodos e classes abstratas em PHP |
Você também poderá gostar das dicas e truques de programação abaixo |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





