 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
C ::: Estruturas de Dados ::: Lista Ligada Simples |
Estruturas de Dados em C - Como inserir antes de um determinado nó em uma lista encadeada simples usando CQuantidade de visualizações: 2076 vezes |
|
Em algumas situações nós precisamos inserir o novo nó antes de um determinado nó na lista encadeada simples. Veja, por exemplo, uma lista com o seguintes valores: 45 | 3 | 98 | 47 Suponha que queremos inserir o valor 50 antes do 98, então o novo conteúdo da lista será: 45 | 3 | 50 | 98 | 47 Observe que neste exemplo eu tratei o caso de inserir antes do primeiro nó, ou seja, antes do 45, mas não tratei a lista vazia. Há também a questão do laço infinito caso o usuário queira inserir antes de um nó não existente (não tratada). Veja o código completo:
#include <stdio.h>
#include <stdlib.h>
// estrutura Nó
struct No{
int valor;
struct No *proximo;
};
// fim da estrutura Nó
// função que permite exibir os valores de
// todos os nós da lista
void exibir(struct No *n){
if(n != NULL){
do{
printf("%d\n", n->valor);
n = n->proximo;
}while(n != NULL);
}
else
printf("A lista esta vazia\n\n");
}
// função que permite inserir um novo nó
// antes de um determinado valor
struct No *inserir_antes_valor(struct No *n, int v, int v_antes){
// reserva memória para o novo nó
struct No *novo = (struct No*)malloc(sizeof(struct No));
novo->valor = v;
// guarda o nó antes do valor que procuramos
struct No *anterior = NULL;
struct No *temp = n; // aponta para o início da lista
// enquanto for diferente do valor que estamos procurando
while(temp->valor != v_antes){
anterior = temp; // anterior recebe temp
// e temp recebe o seu próximo
temp = temp->proximo;
}
// ATENÇÃO: não estamos tratando a condição
// de lista vazia. Para isso veja minha dica
// sobre como inserior no início da lista
// devemos inserior no início da lista?
if(anterior == NULL){
// o próximo do novo nó é o início da lista
novo->proximo = n;
n = novo; // início da lista é o novo nó
}
else{
// o proximo do anterior é o novo nó
anterior->proximo = novo;
// e o próximo do novo nó é temp
novo->proximo = temp;
}
return n;
}
// função que permite inserir nós no
// final da lista.
// veja que a função recebe o valor a ser
// armazenado em cada nó e um ponteiro para o
// início da lista. A função retorna um
// ponteiro para o início da lista
struct No *inserir_final(struct No *n, int v){
// reserva memória para o novo nó
struct No *novo = (struct No*)malloc(sizeof(struct No));
novo->valor = v;
// verifica se a lista está vazia
if(n == NULL){
// é o primeiro nó...não deve apontar para
// lugar nenhum
novo->proximo = NULL;
return novo; // vamos retornar o novo nó como sendo o início da lista
}
else{ // não está vazia....vamos inserir o nó no final
// o primeiro passo é chegarmos ao final da lista
struct No *temp = n; // vamos obter uma referência ao primeiro nó
// vamos varrer a lista até chegarmos ao último nó
while(temp->proximo != NULL){
temp = temp->proximo;
}
// na saída do laço temp aponta para o último nó da lista
// novo será o último nó da lista...o campo próximo dele deve
// apontar para NULL
novo->proximo = NULL;
// vamos fazer o último nó apontar para o nó recém-criado
temp->proximo = novo;
return n; // vamos retornar o início da lista intacto
}
}
int main(int argc, char *argv[])
{
// declara a lista
struct No *inicio = NULL;
// vamos inserir quatro valores no final
// da lista
inicio = inserir_final(inicio, 45);
inicio = inserir_final(inicio, 3);
inicio = inserir_final(inicio, 98);
inicio = inserir_final(inicio, 47);
// vamos exibir a lista
puts("Valores atuais:\n");
exibir(inicio);
// vamos inserir o valor 50 antes do 98
inicio = inserir_antes_valor(inicio, 50, 98);
// vamos exibir a lista novamente
puts("\nValores agora:\n");
exibir(inicio);
puts("\n\n");
system("pause");
return 0;
}
|
LISP ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como converter radianos em graus em LISP - Trigonometria em LISPQuantidade de visualizações: 773 vezes |
|
Todas as funções trigonométricas em Common Lisp (ou AutoLISP, para programadores AutoCAD) recebem seus argumentos em radianos, em vez de graus. Um exemplo disso é a função sin(). Esta função recebe o ângulo em radianos e retorna o seu seno. No entanto, há momentos nos quais precisamos retornar alguns valores como graus. Para isso é importante sabermos fazer a conversão de radianos para graus. Veja a fórmula abaixo: \[Graus = Radianos \times \frac{180}{\pi}\] Agora veja como esta fórmula pode ser escrita em código LISP:
; programa LISP que converte radianos em graus
(let((radianos)(graus))
; valor em radianos
(setq radianos 1.5)
; obtém o valor em graus
(setq graus (* radianos (/ 180 pi)))
; mostra o resultado
(format t "~F radianos em graus é ~F" radianos
graus)
)
Ao executarmos este código LISP nós teremos o seguinte resultado: 1.5 radianos convertidos para graus é 85.94366926962348 Para fins de memorização, 1 radiano equivale a 57,2957795 graus. |
C# ::: Dicas & Truques ::: Matemática e Estatística |
Como resolver uma equação do segundo grau em C# - Como calcular Bhaskara em C#Quantidade de visualizações: 1560 vezes |
|
Como resolver uma equação do 2º grau usando C# Nesta dica mostrarei como encontrar as raízes de uma equação quadrática, ou seja, uma equação do 2º usando a linguagem C#. Definimos como equação do 2º grau ou equações quadráticas qualquer equação do tipo ax² + bx + c = 0 em que a, b e c são números reais e a ≠ 0. Ela recebe esse nome porque, no primeiro membro da igualdade, há um polinômio de grau dois com uma única incógnita. Note que, dos coeficientes a, b e c, somente o a é diferente de zero, pois, caso ele fosse igual a zero, o termo ax² seria igual a zero, logo a equação se tornaria uma equação do primeiro grau: bx + c = 0. Independentemente da ordem da equação, o coeficiente a sempre acompanha o termo x², o coeficiente b sempre acompanha o termo x, e o coeficiente c é sempre o termo independente. Como resolver uma equação do 2º grau Conhecemos como soluções ou raízes da equação ax² + bx + c = 0 os valores de x que fazem com que essa equação seja verdadeira. Uma equação do 2º grau pode ter no máximo dois números reais que sejam raízes dela. Para resolver equações do 2º grau completas, existem dois métodos mais comuns: a) Fórmula de Bhaskara; b) Soma e produto. O primeiro método é bastante mecânico, o que faz com que muitos o prefiram. Já para utilizar o segundo, é necessário o conhecimento de múltiplos e divisores. Além disso, quando as soluções da equação são números quebrados, soma e produto não é uma alternativa boa. Como resolver uma equação do 2º grau usando Bhaskara Como nosso código C# vai resolver a equação quadrática usando a Fórmula de Bhaskara, o primeiro passo é encontrar o determinante. Veja: \[\Delta =b^2-4ac\] Nem sempre a equação possui solução real. O valor do determinante é que nos indica isso, existindo três possibilidades: a) Se determinante > 0, então a equação possui duas soluções reais. b) Se determinante = 0, então a equação possui uma única solução real. c) Se determinante < 0, então a equação não possui solução real. Encontrado o determinante, só precisamos substituir os valores, incluindo o determinante, na Fórmula de Bhaskara: \[x = \dfrac{- b\pm\sqrt{b^2- 4ac}}{2a}\] Vamos agora ao código C#. Nossa aplicação vai pedir para o usuário informar os valores dos três coeficientes a, b e c e, em seguida, vai apresentar as raizes da equação:
using System;
namespace Estudos {
class Principal {
static void Main(string[] args) {
// os coeficientes
double a, b, c;
// as duas raizes, a imaginaria e o discriminante
double raiz1, raiz2, imaginaria, discriminante;
// vamos pedir para o usuário informar os valores dos coeficientes
Console.Write("Valor do coeficiente a: ");
a = Double.Parse(Console.ReadLine());
Console.Write("Valor do coeficiente b: ");
b = Double.Parse(Console.ReadLine());
Console.Write("Valor do coeficiente c: ");
c = Double.Parse(Console.ReadLine());
// vamos calcular o discriminante
discriminante = (b * b) - (4 * a * c);
// a equação possui duas soluções reais?
if (discriminante > 0) {
raiz1 = (-b + Math.Sqrt(discriminante)) / (2 * a);
raiz2 = (-b - Math.Sqrt(discriminante)) / (2 * a);
Console.Write("Existem duas raizes: x1 = " + raiz1
+ " e x2 = " + raiz2);
}
// a equação possui uma única solução real?
else if (discriminante == 0) {
raiz1 = raiz2 = -b / (2 * a);
Console.Write("Existem duas raizes iguais: x1 = "
+ raiz1 + " e x2 = " + raiz2);
}
// a equação não possui solução real?
else if (discriminante < 0) {
raiz1 = raiz2 = -b / (2 * a);
imaginaria = Math.Sqrt(-discriminante) / (2 * a);
Console.Write("Existem duas raízes complexas: x1 = " +
raiz1 + " + " + imaginaria + " e x2 = " + raiz2
+ " - " + imaginaria);
}
Console.WriteLine("\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Valor do coeficiente a: 1 Valor do coeficiente b: 2 Valor do coeficiente c: -3 Existem duas raizes: x1 = 1 e x2 = -3 |
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Python Básico |
Exercício Resolvido de Python - Ler três números inteiros e indicar se eles estão em ordem crescente ou decrescenteQuantidade de visualizações: 954 vezes |
|
Pergunta/Tarefa: Escreva um programa Python que pede para o usuário informar três números inteiros e informa se eles estão em ordem crescente ou decrescente. Se os números estiverem em ordem crescente, escreva "Ordem Crescente". Se estiverem em ordem decrescente, escreva "Ordem Decrescente". Do contrário escreva "Sem ordem definida". Sua saída deverá ser parecida com: Primeiro número: 4 Segundo número: 8 Terceiro número: 11 Ordem Crescente Veja a resolução comentada deste exercício em Python:
# função principal do programa
def main():
# vamos ler três números do usuário
a = int(input("Primeiro número: "))
b = int(input("Segundo número: "))
c = int(input("Terceiro número: "))
# os números estão em ordem crescente?
if a < b and b < c:
print("Ordem Crescente")
# os números estão em ordem decrescente?
elif a > b and b > c:
print("Ordem Decrescente")
# sem ordem definida
else:
print("Sem ordem definida")
if __name__== "__main__":
main()
|
C# ::: Dicas & Truques ::: Data e Hora |
Datas e horas em C# - Como obter o ano da data atual usando a classe Calendar do C#Quantidade de visualizações: 67 vezes |
|
Em algumas situações nós precisamos obter apenas o mês do ano da data atual ou para uma determinada data. Isso pode ser feito por meio de uma chamada ao método GetYear() da classe Calendar da linguagem C#. Veja o código completo para o exemplo:
using System;
using System.Globalization;
namespace Estudos{
class Program{
static void Main(string[] args) {
DateTime agora = DateTime.Now;
Calendar calendario = CultureInfo.InvariantCulture.Calendar;
int ano = calendario.GetYear(agora);
Console.WriteLine("Estamos no ano: {0}", ano);
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código nós teremos o seguinte resultado: Estamos no ano: 2021 |
Portugol ::: Dicas & Truques ::: Cadeias e Caracteres |
Como testar se uma sub-cadeia está contida em uma cadeia de caracteres em Portugol usando a função posicao_texto()Quantidade de visualizações: 525 vezes |
|
Nesta dica mostrarei como podemos verificar se uma substring está contida em uma string em Portugol. Para isso nós vamos usar a função posicao_texto() da biblioteca Texto. A função posicao_texto() pede a sub-cadeia a ser pesquisada, a cadeia na qual a pesquisa será feita e o índice do primeiro caractere a partir do qual a sub-string será pesquisada. Se a substring for encontrada, a função retorna a posição do primeiro caractere. Caso contrário o valor -1 será retornado. Veja o código completo para um programa Portugol no qual testamos se uma palavra está contida em uma frase:
programa {
// vamos importar a biblioteca Texto
inclua biblioteca Texto --> tx
funcao inicio() {
// vamos criar uma frase
cadeia frase = "Gosto de programar em Portugol"
// vamos criar uma sub-cadeia
cadeia palavra = "Portugol"
// vamos verificar se a sub-cadeia está contida na cadeia
se (tx.posicao_texto(palavra, frase, 0) != -1) {
escreva("A substring está contida na string")
}
senao {
escreva("A substring não está contida na string")
}
}
}
Ao executar este código Portugol nós teremos o seguinte resultado: A substring está contida na string. |
Java ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a equação reduzida da reta em Java dados dois pontos pertencentes à retaQuantidade de visualizações: 1418 vezes |
|
Nesta dica de Java veremos como calcular a equação reduzida da reta quando temos dois pontos pertencentes à esta reta. Não, nessa dica não vamos calcular a equação geral da reta, apenas a equação reduzida. Em outras dicas do site você encontra como como isso pode ser feito. Para relembrar: a equação reduzida da reta é y = mx + n, em que x e y são, respectivamente, a variável independente e a variável dependente; m é o coeficiente angular, e n é o coeficiente linear. Além disso, m e n são números reais. Com a equação reduzida da reta, é possível calcular quais são os pontos que pertencem a essa reta e quais não pertencem. Vamos começar então analisando a seguinte figura, na qual temos dois pontos que pertencem à uma reta: 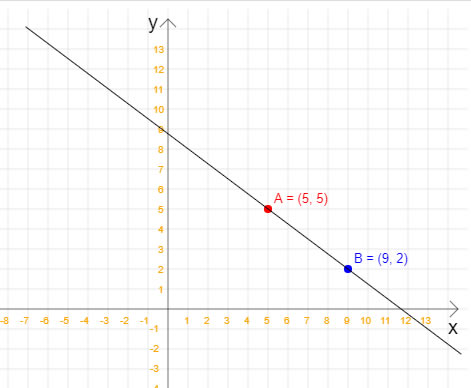 Note que a reta da figura passa pelos pontos A(5, 5) e B(9, 2). Então, uma vez que já temos os dois pontos, já podemos calcular a equação reduzida da reta. Veja o código Java completo para esta tarefa:
package estudos;
import java.util.Scanner;
public class Estudos{
public static void main(String[] args){
// vamos usar a classe Scanner para ler os dados
Scanner entrada = new Scanner(System.in);
// vamos ler as coordenadas do primeiro ponto
System.out.print("Coordenada x do primeiro ponto: ");
double x1 = Double.parseDouble(entrada.nextLine());
System.out.print("Coordenada y do primeiro ponto: ");
double y1 = Double.parseDouble(entrada.nextLine());
// vamos ler as coordenadas do segundo ponto
System.out.print("Coordenada x do segundo ponto: ");
double x2 = Double.parseDouble(entrada.nextLine());
System.out.print("Coordenada y do segundo ponto: ");
double y2 = Double.parseDouble(entrada.nextLine());
String sinal = "+";
// vamos calcular o coeficiente angular da reta
double m = (y2 - y1) / (x2 - x1);
// vamos calcular o coeficiente linear
double n = y1 - (m * x1);
// coeficiente linear menor que zero? O sinal será negativo
if (n < 0){
sinal = "-";
n = n * -1;
}
// mostra a equação reduzida da reta
System.out.println("Equação reduzida: y = " + m + "x"
+ " " + sinal + " " + n);
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 5 Coordenada y do primeiro ponto: 5 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 2 Equação reduzida: y = -0,75x + 8,75 Para testarmos se nossa equação reduzida da reta está realmente correta, considere o valor 3 para o eixo x da imagem acima. Ao efetuarmos o cálculo: >> y = (-0.75 * 3) + 8.75 y = 6.5000 temos o valor 6.5 para o eixo y, o que faz com que o novo ponto caia exatamente em cima da reta considerada na imagem. |
jQuery ::: Dicas & Truques ::: Manipulação e Conteúdo Dinâmico |
Como definir o conteúdo HTML de um elemento usando a função html() do jQueryQuantidade de visualizações: 7915 vezes |
O método html("conteúdo") permite definir o conteúdo (innerHTML) de todos os elementos encontrados em uma determinada condição. Considere os seguintes elementos P:<p>Sou o primeiro parágrafo</p> <p>Sou o segundo parágrafo</p> Veja agora o código JavaScript que define o conteúdo HTML destes dois parágrafos:
<script type="text/javascript">
<!--
function definirInnerHTML(){
var texto = "<b>Veja este texto</b>";
// define o conteúdo para os elementos P
$('p').html(texto);
}
//-->
</script>
Lembre, porém, que a prática mais comum é definir o conteúdo HTML de um elemento identificado por um id. O retorno deste método é um objeto jQuery, que pode ser usado para possíveis encadeamentos de chamadas de métodos. |
Java ::: Dicas & Truques ::: Gráficos |
Como desenhar em um JComponent do Java Swing (JLabel, JButton, JPanel, etc) usando o método paintComponent()Quantidade de visualizações: 10188 vezes |
|
A classe JComponent possui um método chamado paintComponent(Graphics g) que recebe um objeto da classe Graphics que pode ser usado para desenhar na superfície do componente. Desta forma, qualquer componente que herda de JComponent pode ser usado para esta finalidade. Para demonstrar como isso é feito, veja um trecho de código no qual desenhamos uma linha em um JLabel e o anexamos à janela do aplicativo. Observe a criação de uma classe personalizada que herda de JLabel:
import java.awt.*;
import javax.swing.*;
public class Estudos extends JFrame{
public Estudos() {
super("Desenhando em um JLabel");
Container c = getContentPane();
// Cria o JLabel
MinhaLabel label = new MinhaLabel();
c.add(label);
setSize(350, 250);
setVisible(true);
}
public static void main(String args[]){
Estudos app = new Estudos();
app.setDefaultCloseOperation(
JFrame.EXIT_ON_CLOSE);
}
}
// classe personalizada que permite desenhar
class MinhaLabel extends JLabel{
protected void paintComponent(Graphics g){
super.paintComponent(g);
g.drawLine(0, 0, 200, 200);
}
}
|
C ::: Dicas & Truques ::: Strings e Caracteres |
Como contar as ocorrências de uma substring em uma string em C usando uma função substring_count() personalizadaQuantidade de visualizações: 10385 vezes |
Em algumas situações precisamos obter a quantidade de vezes que uma substring ocorre dentro de uma string. Para isso podemos usar a função personalizada substring_count(). Esta função recebe a string e a substring que desejamos pesquisar e retorna um inteiro contendo a quantidade de vezes que a substring foi encontrada. Veja o código:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// função personalizada que permite contar as
// ocorrências de uma substring em uma string
int substring_count(const char *str, const char *substring){
int i, j, k, quant = 0;
// vamos percorrer todos os caracteres da string
for(i = 0; str[i]; i++){
for(j = i, k = 0; str[j] == substring[k]; j++, k++){
if(substring[k + 1] == 0) // fim da comparação
quant++;
}
}
return quant;
}
int main(int argc, char *argv[]){
char frase[] = "Gosto muito de Java, JavaScript e Python";
printf("Ocorrencias encontradas: %d",
substring_count(frase, "Java"));
puts("\n\n");
system("PAUSE");
return 0;
}
|
Nossas 20 dicas & truques de programação mais populares |
|
MySQL - Como retornar a hora atual no MySQL usando as funções CURTIME(), CURRENT_TIME e CURRENT_TIME() |
Você também poderá gostar das dicas e truques de programação abaixo |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




