 |
|||||
|
|||||
JavaScript ::: Dicas & Truques ::: Matemática e Estatística |
Como elevar uma base a um determinado expoente usando o método pow() do objeto Math do JavaScriptQuantidade de visualizações: 24804 vezes |
Em algumas situações nós precisamos efetuar cálculos de potenciação em JavaScript, ou seja, elevar um número (uma base) a um determinado expoente e obter sua potência. Veja a figura a seguir: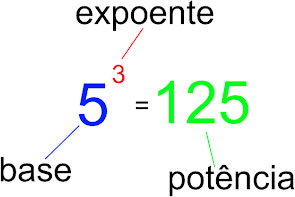 Veja que aqui o valor 5 foi elevado ao cubo, ou seja, ao expoente 3 e obtemos como resultado sua potência: 125. A linguagem JavaScript nos fornece o método pow(), como parte do objeto Math, que recebe como argumentos a base e o expoente e nos retorna a potência. Veja um exemplo de seu uso no código abaixo:
<!doctype html>
<html>
<head>
<title>Estudos JavaScript</title>
</head>
<body>
<script type="text/javascript">
var base = 4;
var expoente = 5;
var potencia = Math.pow(4, 5);
document.write("A base " + base + " elevada ao expoente "
+ expoente + " é igual à potência " + potencia);
</script>
</body>
</html>
Ao executarmos este código JavaScript nós teremos o seguinte resultado: A base 4 elevada ao expoente 5 é igual a potencia 1024 |
C ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Tenha cuidado com os limites dos índices de um vetor ou matriz na linguagem CQuantidade de visualizações: 9913 vezes |
|
Um erro muito comum em programas C ocorre quando não atentamos para os limites dos índices de um vetor ou matriz. Como sabemos, os índices iniciam em 0 e vão até o tamanho do vetor menos 1. Porém, ao contrário de outras linguagens, o C (compiladores sendo usados em 2007 e 2008) não evita que este limite seja ultrapassado. O resultado disso é que o programa acaba lendo posições de memória inexistentes ou pertecentes a outros programas. Veja um trecho de código no qual acessamos uma posição inválida no vetor valores. Este código foi testado no MinGW 3.4.2 e compilou e executou sem qualquer mensagem de advertência.
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[])
{
// array com 5 inteiros
int valores[] = {23, 6, 45, 9, 3};
// acessa um índice além dos limites do array
// lembre-se de que os índices iniciam em 0
int valor = valores[5];
// exibe o resultado
printf("%d\n\n", valor);
system("PAUSE");
return 0;
}
Ao executar este código nós teremos o seguinte resultado (o seu vai ser diferente, é claro): -858993460 Minha recomendação é: se você quer mesmo programar na linguagem C, crie uma forma de impedir o acesso à índices inválidos. Se isso acontecer, os resultados exibidos pelos seus programas poderão ser realmente inesperados. |
GNU Octave ::: Desafios e Lista de Exercícios Resolvidos ::: Pesquisa Operacional |
Exercício Resolvido de Octave - Programação Linear - Um fazendeiro decidiu misturar duas rações, a Ração X e a Ração Y. Cada porção de ração dada aos animaisQuantidade de visualizações: 425 vezes |
|
Pergunta/Tarefa: Este exercício de Octave aborda o uso da função glpk() para resolver um problema de Pesquisa Operacional usando Programação Linear. 1) Um fazendeiro decidiu misturar duas rações, a Ração X e a Ração Y. Cada porção de ração dada aos animais exige 60g de proteína e 30g de gordura. A Ração X possui 15g de proteína e 10g de gordura, e custa R$ 80,00 a unidade. A Ração Y apresenta 20g de proteína e 5g de gordura e custa R$ 50,00 a unidade. Quanto de cada ração deve ser usada para minimizar os custos do fazendeiro? Sua saída deverá ser parecida com: A solução para o problema de minimização é: x = 2.40 y = 1.20 O custo mínimo é: 252.00 Antes de passarmos ao código Octave, vamos fazer a modelagem matemática do problema. O primeiro passo é identificar as variáveis. Assim, vamos chamar de x o número de unidades da Ração X e de y o número de unidades da Ração Y. Veja: x = Número de unidades da Ração X y = Número de unidades da Ração Y E então temos a função custo: custo = 80x + 50y A primeira restrição diz respeito à quantidade de proteína em cada porção de ração. Sabendo que a Ração X apresenta 15g de proteína e a Ração Y apresenta 20g de proteína nós temos: R1: 15x + 20y >= 60 (proteína) A segunda restrição diz respeito à quantidade de gordura em cada porção de ração. Sabendo que a Ração X apresenta 10g de gordura e a Ração Y apresenta 5g de gordura nós temos: R2: 10x + 5y >= 30 (gordura) As restrições R3 e R4 dizem respeito à não negatividade das variáveis de decisão: R3: x >= 0 R4: y >= 0 Veja agora o código Octave completo (pesquisa_operacional.m):
# vamos começar definindo a matriz que representa a função de
# minimização
c = [80.0, 50.0]';
# agora a matriz de restrições
A = [15, 20; 10, 5];
b = [60, 30]';
# as restrições de não negatividade e o limite superior
lb = [0, 0]';
ub = [];
# definimos as restrições como limites inferiores
ctype = "LL";
# indicamos que vamos usar variáveis contínuas (não inteiros)
vartype = "CC";
# vamos usar minimização, por isso definimos o valor 1. Se fosse
# maximização o valor seria -1
s = 1;
# definimos os parâmetros adicionais
param.msglev = 1;
param.itlim = 100;
# e chamamos a função glpk()
[xmin, fmin, status, extra] = glpk(c, A, b, lb, ub, ctype, vartype, s, param);
# mostramos a solução para o problema de minimização
printf("A solução para o problema de minimização é:\n\n");
printf("x = %.2f\n", xmin(1));
printf("y = %.2f\n", xmin(2));
# para finalizar vamos mostrar o custo mínimo
printf("\nO custo mínimo é: %.2f\n\n", fmin);
Ao executar o código você perceberá que, para minimizar os custos do fazendeiro, deverão ser usados na mistura 2,4 unidades da Ração X e 1,2 unidades da Raça Y, a um custo mínimo de R$ 252,00. |
Python ::: Dicas & Truques ::: Strings e Caracteres |
Como testar se uma string contém apenas letras em Python usando a função isalpha()Quantidade de visualizações: 15036 vezes |
Este exemplo mostra como podemos a função isalpha() do Python para verificar se uma string contém apenas letras, ou seja, nada de números, espaços nem pontuação. Se algum número, espaço, um caractere especial ou pontuação estiver contido, a função retorna False.
def main():
# uma palavra contendo apenas letras
palavra = "Arquivo"
# a palavra contém apenas letras?
if palavra.isalpha():
print("A string contém apenas letras")
else:
print("A string não contém somente letras")
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: A string contém apenas letras. |
Delphi ::: VCL - Visual Component Library ::: TListBox |
Como usar o controle TListBox em suas aplicações DelphiQuantidade de visualizações: 13955 vezes |
|
Objetos da classe TListBox, da unit StdCtrls, são controles do tipo lista de seleção. Este componente exibe uma lista com barras de rolagem contendo items que podem ser selecionados, adicionados ou excluídos. A classe TListBox é um wrapper (invólucro) para o controle LISTBOX da plataforma Windows. Em controles do tipo ListBox o usuário pode selecionar apenas um ítem ou vários itens de uma vez. Em Delphi, a classe TListBox implementa o comportamento genérico definido em TCustomListBox. É esta classe que devemos usar para derivar nossa própria ListBox caso o controle TListBox não satisfaça as nossas necessidades. É claro que podemos partir de qualquer classe que herde de TCustomListBox. A forma mais comum de adicionarmos um controle TListBox em nossos formulários é selecionando este componente na aba Standard e arrastando-o para a posição desejada na janela. Em seguida podemos adicionar itens na lista acessando sua propriedade Items, que são do tipo TStrings, ou seja, uma lista de strings. Ao clicarmos na propriedade Items no Object Inspector, um String List Editor será exibido. Basta inserir algumas strings nesta caixa de texto, pressionar o botão OK e verificar como o controle já exibe os itens que acabamos de inserir. Em tempo de execução, itens podem ser adicionados à uma TListBox usando códigos parecidos com:
procedure TForm1.Button1Click(Sender: TObject);
begin
// vamos inserir um novo item na TListBox
ListBox1.Items.Add('Osmar J. Silva');
end;
Se precisarmos obter o texto do ítem selecionado em uma TListBox, podemos usar: procedure TForm1.Button1Click(Sender: TObject); begin // vamos obter o texto do item selecionado na TListBox ShowMessage(ListBox1.Items[ListBox1.ItemIndex]); end; Para fins de compatibilidade, esta dica foi escrita usando Delphi 2009. |
Java ::: Topografia e Geoprocessamento ::: Passos Iniciais |
Como converter graus, minutos e segundos para graus decimais em JavaQuantidade de visualizações: 525 vezes |
|
Em algumas situações, principalmente em cálculos da Engenharia Civil e Topografia, nós precisamos converter graus, minutos e segundos para graus decimais. É comum chamarmos graus, minutos e segundos de DMS ou GMS, enquanto os graus decimais são chamados de UTM. Nesta dica veremos como converter 85º 42' 13.75'' para graus decimais. A fórmula que usaremos é a seguinte: \[\text{Graus decimais} = \text{Graus} + \frac{\text{Minutos}}{60} + \frac{\text{Segundos}}{3600} \] Veja agora o código Java completo que pede para o usuário informar os graus, os minutos e os segundos e mostra os graus decimais:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// vamos pedir para o usuário informar os graus, minutos
// e segundos
System.out.print("Informe os graus: ");
double graus = Double.parseDouble(entrada.nextLine());
System.out.print("Informe os minutos: ");
double minutos = Double.parseDouble(entrada.nextLine());
System.out.print("Informe os segundos: ");
double segundos = Double.parseDouble(entrada.nextLine());
// agora vamos calcular os graus decimais
double grausDecimais = graus + (minutos / 60.0) +
(segundos / 3600.0);
// e agora mostramos o resultado
System.out.println("Os graus decimais são: " + grausDecimais);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Informe os graus: 85 Informe os minutos: 42 Informe os segundos: 13.75 Os graus decimais são: 85.70381944444445 Fique atento ao sinal. Se o valor em graus, minutos e segundos possuir os caracteres "W" ou "S", então o valor em graus decimais deverá levar o sinal de negativo. |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Programação Orientada a Objetos |
POO - Programação Orientada a Objetos - Exercícios Resolvidos de Java - Ex. 2 - A classe Circulo (construtores, métodos, getters e setters e encapsulamento)Quantidade de visualizações: 19794 vezes |
|
Pergunta/Tarefa: Escreva uma classe Circulo para representar círculos. Esta classe deverá conter os seguintes atributos e métodos: a) Uma variável privada do tipo double chamada raio que guardará o valor do raio atual do circulo. b) Métodos get() e set() públicos que permitem definir e acessar o valor da variável raio. c) Um construtor que recebe o valor do raio como argumento. d) Um método getArea() que calcula e retorna a área do círculo. e) Um método getCircunferencia() que calcula e retorna a circunferência do círculo. f) Um método aumentarRaio() que recebe um valor double e o usa como percentual para aumentar o raio do círculo. Crie uma classe contendo um método main() para testar a funcionalidade da classe Circulo. Eis um exemplo de entrada e saída: 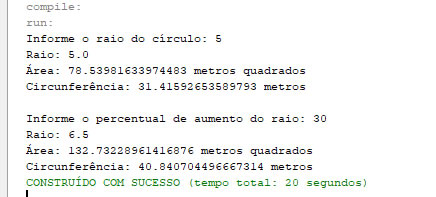 Resposta/Solução: Veja a resolução comentada deste exercício usando Java console: Circulo.java:
package estudos;
public class Circulo{
private double raio; // guarda o raio atual do círculo
// construtor que recebe o valor do raio como argumento
public Circulo(double raio){
this.raio = raio;
}
// permite obter o raio do círculo
public double getRaio(){
return raio;
}
// permite definir o raio do círculo
public void setRaio(double raio){
this.raio = raio;
}
// obtém a área do círculo
public double getArea(){
double area = Math.PI * Math.pow(this.raio, 2);
return area;
}
// obtém a circunferência do círculo
public double getCircunferencia(){
double circunferencia = (2 * Math.PI) * this.raio;
return circunferencia;
}
// permite aumentar o raio de acordo com uma porcentagem fornecida
public void aumentarRaio(double porcentagem){
this.raio = this.raio + (porcentagem / 100.0) * this.raio;
}
}
Veja agora o método main() que nos permite testar a funcionalidade da classe Circulo:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
// vamos criar uma instância da classe Circulo
Scanner entrada = new Scanner(System.in);
System.out.print("Informe o raio do círculo: ");
double raio = Double.parseDouble(entrada.nextLine());
Circulo c = new Circulo(raio);
// vamos mostrar o valor do raio atual
System.out.println("Raio: " + c.getRaio());
// vamos mostrar a área
System.out.println("Área: " + c.getArea() + " metros quadrados");
// vamos mostrar a circunferência
System.out.println("Circunferência: " + c.getCircunferencia() + " metros");
// vamos aumentar o raio do circulo em uma determinada porcentagem
System.out.print("\nInforme o percentual de aumento do raio: ");
double percentual = Double.parseDouble(entrada.nextLine());
c.aumentarRaio(percentual);
// vamos mostrar o valor do raio atual
System.out.println("Raio: " + c.getRaio());
// vamos mostrar a área
System.out.println("Área: " + c.getArea() + " metros quadrados");
// vamos mostrar a circunferência
System.out.println("Circunferência: " + c.getCircunferencia() + " metros");
}
}
|
VisuAlg ::: Dicas & Truques ::: Matemática e Estatística |
Como resolver uma equação do segundo grau em VisuAlg - Como calcular Bhaskara em VisuAlgQuantidade de visualizações: 1810 vezes |
|
Como resolver uma equação do 2º grau usando VisuAlg Nesta dica mostrarei como encontrar as raízes de uma equação quadrática, ou seja, uma equação do 2º usando um algoritmo escrito na ferramenta VisuAlg, uma das preferidas para o aprendizado de algoritmos e lógica de programação. Definimos como equação do 2º grau ou equações quadráticas qualquer equação do tipo ax² + bx + c = 0 em que a, b e c são números reais e a ≠ 0. Ela recebe esse nome porque, no primeiro membro da igualdade, há um polinômio de grau dois com uma única incógnita. Note que, dos coeficientes a, b e c, somente o a é diferente de zero, pois, caso ele fosse igual a zero, o termo ax² seria igual a zero, logo a equação se tornaria uma equação do primeiro grau: bx + c = 0. Independentemente da ordem da equação, o coeficiente a sempre acompanha o termo x², o coeficiente b sempre acompanha o termo x, e o coeficiente c é sempre o termo independente. Como resolver uma equação do 2º grau Conhecemos como soluções ou raízes da equação ax² + bx + c = 0 os valores de x que fazem com que essa equação seja verdadeira. Uma equação do 2º grau pode ter no máximo dois números reais que sejam raízes dela. Para resolver equações do 2º grau completas, existem dois métodos mais comuns: a) Fórmula de Bhaskara; b) Soma e produto. O primeiro método é bastante mecânico, o que faz com que muitos o prefiram. Já para utilizar o segundo, é necessário o conhecimento de múltiplos e divisores. Além disso, quando as soluções da equação são números quebrados, soma e produto não é uma alternativa boa. Como resolver uma equação do 2º grau usando Bhaskara Como nosso algoritmo VisuAlg vai resolver a equação quadrática usando a Fórmula de Bhaskara, o primeiro passo é encontrar o determinante. Veja: \[\Delta =b^2-4ac\] Nem sempre a equação possui solução real. O valor do determinante é que nos indica isso, existindo três possibilidades: a) Se determinante > 0, então a equação possui duas soluções reais. b) Se determinante = 0, então a equação possui uma única solução real. c) Se determinante < 0, então a equação não possui solução real. Encontrado o determinante, só precisamos substituir os valores, incluindo o determinante, na Fórmula de Bhaskara: \[x = \dfrac{- b\pm\sqrt{b^2- 4ac}}{2a}\] Vamos agora ao código VisuAlg. Nossa aplicação vai pedir para o usuário informar os valores dos três coeficientes a, b e c e, em seguida, vai apresentar as raizes da equação:
Algoritmo "Como resolver uma equação do 2º grau usando VisuAlg"
Var
// variáveis usadas na resolução do problema
// os coeficientes
a, b, c: real
// as duas raizes, a imaginaria e o discriminante
raiz1, raiz2, imaginaria, discriminante: real
Inicio
// vamos pedir para o usuário informar os valores dos coeficientes
escreva("Valor do coeficiente a: ")
leia(a)
escreva("Valor do coeficiente b: ")
leia(b)
escreva("Valor do coeficiente c: ")
leia(c)
// vamos calcular o discriminante
discriminante <- (b * b) - (4 * a * c)
// a equação possui duas soluções reais?
se discriminante > 0 então
raiz1 <- (-b + raizq(discriminante)) / (2 * a)
raiz2 <- (-b - raizq(discriminante)) / (2 * a)
escreva("Duas raizes: x1 = ", raiz1, " e x2 = ", raiz2)
senão
// a equação possui uma única solução real?
se discriminante = 0 então
raiz1 <- -b / (2 * a)
raiz2 <- -b / (2 * a)
escreva("Duas raizes iguais: x1 = ", raiz1, " e x2 = ", raiz2)
// a equação não possui solução real?
senão
raiz1 <- -b / (2 * a)
raiz2 <- -b / (2 * a)
imaginaria <- raizq(-discriminante) / (2 * a)
escreva("Existem duas raízes complexas: ")
escreva("x1 = ", raiz1, " + " ,imaginaria, " e x2 = ", raiz2, " - ", imaginaria)
fimse
fimse
Fimalgoritmo
Ao executar este código VisuAlg nós teremos o seguinte resultado: Valor do coeficiente a: 1 Valor do coeficiente b: 2 Valor do coeficiente c: -3 Existem duas raizes: x1 = 1.0 e x2 = -3.0 |
Java ::: Dicas & Truques ::: Internacionalização e Localização (Internationalization, i18n, Localization, l10n) |
Como obter a localização padrão da JVM usando o método getDefault() da classe Locale da linguagem JavaQuantidade de visualizações: 9078 vezes |
Em algumas situações precisamos fazer a internacionalização de nossas aplicações. Isso implica em usar um objeto da classe Locale para aplicar a formatação de datas, horas e valores de acordo com as configurações regionais do usuário. Porém, antes de alterar o Locale padrão da JVM, é importante sabermos mais sobre ele. Para isso temos o método estático getDefault() da classe Locale:public static Locale getDefault() Este método retorna um objeto da classe Locale que nos permitirá obter informações sobre a língua, o país e demais configurações do ambiente. Veja um trecho de código demonstrando seu uso:
import java.util.*;
public class Estudos{
public static void main(String args[]){
// obtém o Locale padrão da JVM
Locale locale = Locale.getDefault();
// vamos exibir o código da linguagem e nome do
// país para o Locale obtido
System.out.println(locale.getLanguage() + " - "
+ locale.getDisplayCountry());
}
}
O resultado da execução deste código será algo como: pt - Brasil |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercício Resolvido de Java - Como rotacionar os elementos de um vetor de inteiros n vezes para a direita - Solução usando vetor temporárioQuantidade de visualizações: 690 vezes |
|
Pergunta/Tarefa: Dado o vetor:
// vamos criar um vetor de inteiros
int valores[] = {1, 6, 9, 3, 7, 8, 5, 2};
Importante: a solução que apresentamos usa um array adicional para resolver o desafio. Fique à vontade para usar força-bruta ou outra abordagem que achar mais conveniente. Sua saída deverá ser parecida com: Array na ordem original: 1 6 9 3 7 8 5 2 Rotação do vetor no passo 1 do primeiro laço: 8 0 0 0 0 0 0 0 Rotação do vetor no passo 2 do primeiro laço: 8 5 0 0 0 0 0 0 Rotação do vetor no passo 3 do primeiro laço: 8 5 2 0 0 0 0 0 Rotação do vetor no passo 1 do segundo laço: 8 5 2 1 0 0 0 0 Rotação do vetor no passo 2 do segundo laço: 8 5 2 1 6 0 0 0 Rotação do vetor no passo 3 do segundo laço: 8 5 2 1 6 9 0 0 Rotação do vetor no passo 4 do segundo laço: 8 5 2 1 6 9 3 0 Rotação do vetor no passo 5 do segundo laço: 8 5 2 1 6 9 3 7 Array depois de rotacionar 3 vezes: 8 5 2 1 6 9 3 7 Veja a resolução comentada deste exercício em Java:
package estudos;
public class Estudos {
public static void main(String[] args) {
// vamos criar um vetor de inteiros
int valores[] = {1, 6, 9, 3, 7, 8, 5, 2};
// mostramos o array na ordem original
System.out.println("Array na ordem original:");
exibirVetor(valores);
// vamos rotacionar o array 3 casas para a direita
valores = rotacionarArray(valores, 3);
// e mostramos o resultado
System.out.println("Array depois de rotacionar 3 vezes:");
exibirVetor(valores);
}
// método usado para exibir o array
public static void exibirVetor(int []vetor){
// percorremos cada elemento do vetor
for (int i = 0; i < vetor.length; i++) {
System.out.print(vetor[i] + " ");
}
System.out.println("\n");
}
// método que recebe um vetor de inteiros e o rotaciona um
// determinado número de vezes
public static int[] rotacionarArray(int[] vetor, int n) {
// vamos obter a quantidade de elementos no vetor
int quant = vetor.length;
// o número de rotações é maior que a quantidade de
// elementos no vetor? Se for nós ajustamos o número
// de rotações usando o operador de módulo
if(n > quant){
n = n % quant;
}
// criamos um vetor temporário
int[] resultado = new int[quant];
// o primeiro laço movimenta os elementos a partir
// do valor de n
for(int i = 0; i < n; i++){
resultado[i] = vetor[quant - n + i];
// mostramos o progresso
System.out.println("Rotação do vetor no passo " + (i + 1) +
" do primeiro laço:");
exibirVetor(resultado);
}
// ajustamos o índice para o primeiro elemento do vetor
int indice = 0;
for(int i = n; i < quant; i++){
resultado[i] = vetor[indice];
// mostramos o progresso
System.out.println("Rotação do vetor no passo " + (indice + 1) +
" do segundo laço:");
exibirVetor(resultado);
indice++; // incrementa o índice
}
// retorna o vetor rotacionado
return resultado;
}
}
A solução que apresentamos aqui usa um vetor temporário, isto é, um array adicional, para melhorar a perfomance. Em outras dicas do site nós apresentamos uma solução para este desafio usando força-bruta. A força-bruta não é a melhor abordagem, mas pode ser mais fácil de ser entendida por iniciantes em programação. |
Nossas 20 dicas & truques de programação mais populares |
|
Java - Como remover itens repetidos de uma ArrayList usando um objeto da classe LinkedHashSet do Java |
Você também poderá gostar das dicas e truques de programação abaixo |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





