Node.js ::: Node.js + MongoDB ::: Passos Iniciais |
Node.js MongoDB - Como instalar o driver do MongoDB no Node.js e efetuar uma conexão Node.js + MongoDBQuantidade de visualizações: 1526 vezes |
|
Assumindo que você já conhece o banco de dados MongoDB, já fez sua instalação e já está um pouco familiarizado com suas características, nesta dica mostrarei como podemos efetuar uma conexão Node.js + MongoDB. Este é o passo inicial para desenvolver aplicações MEAN (Mongo, Express, Angular, Node) ou MERN (Mongo, Express, React, Node). Note que, nessa dica, usarei apenas o MongoClient para efetuar a conexão com o banco de dados MongoDB. Em outras dicas eu abordo o Mongoose. Então vamos iniciar. A primeira coisa que temos que fazer é instalar o driver MongoDB. Assim, com o Node.js devidamente instalado e funcionando, e com o banco MongoDB em perfeito funcionamento também, abra uma janela de terminal e digite o comando: npm install mongodb Após alguns minutos, a instalação será concluída e teremos o seguinte resultado: + mongodb@3.6.4 added 17 packages from 9 contributors and audited 20 packages in 9.358s 1 package is looking for funding run `npm fund` for details found 0 vulnerabilities Agora já podemos escrever o código que efetua a conexão Node.js com o MongoDB. Abra o seu editor de códigos favorito e digite a listagem abaixo:
// vamos obter uma referência ao MongoClient
var MongoClient = require('mongodb').MongoClient;
// vamos nos conectar à base de dados escola
var url = 'mongodb://localhost:27017/escola';
// Vamos nos conectar ao servidor e base de dados. Atenção: Em caso de erro, a
// função pode demorar a retornar, pois o Node.js pode pensar que é lentidão
// na rede
MongoClient.connect(url, {useUnifiedTopology: true}, function(err, db) {
if(err){
console.log("Não foi possível efetuar a conexão. Erro: " + err);
}
else{
console.log("Conexão efetuada com sucesso.");
}
// finalmente vamos fechar a conexao
if(db){
db.close();
}
});
Salve este código como conexao.js e execute-o no Node.js (com o MongoDB rodando, é claro) com o seguinte comando: c:\estudos_nodejs>node conexao.js Se tudo correr bem você verá a mensagem: Conexão efetuada com sucesso. Veja que, nesse código, eu efetuei uma conexão com a base de dados escola. Se a porta e o servidor estiverem corretos (talvez você tenha que informar um usuário e senha também), a conexão será efetuada com sucesso mesmo que a base de dados não exista. Quando informamos uma base de dados inexistente, o MongoDB entende que queremos criá-la, mas ele só a cria de fato, quando solicitamos a criação de uma nova coleção. Em mais dicas dessa seção você aprenderá como criar coleções no MongoDB a partir de seus códigos Node.js. Até lá e bons estudos. |
C# ::: Dicas & Truques ::: Data e Hora |
Como calcular a quantidade de dias decorridos em C# usando um objeto TimeSpanQuantidade de visualizações: 8518 vezes |
Em algumas ocasiões precisamos saber a quantidade de dias decorridos deste uma determinada data usando a linguagem C#. O trecho de código abaixo mostra como isso pode ser feito. Veja que usamos o construtor da estrutura DateTime para construir a data no passado e então a subtraímos da data atual. Em seguida obtemos a quantidade de dias do TimeSpan resultante:
using System;
namespace Estudos {
class Program {
static void Main(string[] args) {
// vamos obter a quantidade de dias decorridos entre
// 10/06/2009 e a data atual
DateTime data_anterior = new DateTime(2009, 6, 10); // 10/06/2009
DateTime hoje = DateTime.Now;
// obtém a quantidade de dias decorridos
TimeSpan dif = hoje.Subtract(data_anterior);
int decorridos = dif.Days;
// exibe o resultado
System.Console.WriteLine("Dias decorridos desde 10/06/2009: " +
decorridos);
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Dias decorridos desde 10/06/2009: 4662 |
Java ::: Dicas & Truques ::: Fuso Horários |
Como retornar uma lista de todos os IDs de fusos horários suportados pela linguagem Java usando o método getAvailableIDs() da classe TimeZoneQuantidade de visualizações: 9021 vezes |
A linguagem Java, por meio da classe TimeZone, nos permite trabalhar com uma enorme variedade de fusos horários. No entanto, antes de assumir que um determinado fuso horário é suportado, é interessante verificar se tal fuso horário está na lista de IDs suportados. Isso pode ser feito com uma chamada ao método estático getAvailableIDs(). Este método retorna o ID de todos os fusos horários suportados. Veja um exemplo de como usá-lo:
import java.util.*;
public class Estudos{
public static void main(String args[]){
// obtém todos os IDs de fusos horários
// disponíveis na classe TimeZone
String fusos[] = TimeZone.getAvailableIDs();
for(int i = 0; i < fusos.length; i++){
System.out.println(fusos[i]);
}
}
}
Ao executar este código você terá um resultado semelhante à (optamos por listar apenas os 100 primeiros resultados): Etc/GMT+12 Etc/GMT+11 MIT Pacific/Apia Pacific/Midway Pacific/Niue Pacific/Pago_Pago Pacific/Samoa US/Samoa America/Adak America/Atka Etc/GMT+10 HST Pacific/Fakaofo Pacific/Honolulu Pacific/Johnston Pacific/Rarotonga Pacific/Tahiti SystemV/HST10 US/Aleutian US/Hawaii Pacific/Marquesas AST America/Anchorage America/Juneau America/Nome America/Yakutat Etc/GMT+9 Pacific/Gambier SystemV/YST9 SystemV/YST9YDT US/Alaska America/Dawson America/Ensenada America/Los_Angeles America/Tijuana America/Vancouver America/Whitehorse Canada/Pacific Canada/Yukon Etc/GMT+8 Mexico/BajaNorte PST PST8PDT Pacific/Pitcairn SystemV/PST8 SystemV/PST8PDT US/Pacific US/Pacific-New America/Boise America/Cambridge_Bay America/Chihuahua America/Dawson_Creek America/Denver America/Edmonton America/Hermosillo America/Inuvik America/Mazatlan America/Phoenix America/Shiprock America/Yellowknife Canada/Mountain Etc/GMT+7 MST MST7MDT Mexico/BajaSur Navajo PNT SystemV/MST7 SystemV/MST7MDT US/Arizona US/Mountain America/Belize America/Cancun America/Chicago America/Costa_Rica America/El_Salvador America/Guatemala America/Indiana/Knox America/Indiana/Petersburg America/Indiana/Vincennes America/Knox_IN America/Managua America/Menominee America/Merida America/Mexico_City America/Monterrey America/North_Dakota/Center America/North_Dakota/New_Salem America/Rainy_River America/Rankin_Inlet America/Regina America/Swift_Current America/Tegucigalpa America/Winnipeg CST CST6CDT Canada/Central Canada/East-Saskatchewan Canada/Saskatchewan Chile/EasterIsland Um bom uso deste método é quando estamos desenvolvendo uma aplicação que mostra o horário ao redor do mundo. Podemos ter uma lista de fusos horários e, mediante a seleção do usuário, fornecer o valor selecionado para o método setTimeZone() da classe Calendar, por exemplo. |
PHP ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cateto oposto dadas as medidas da hipotenusa e do cateto adjascente em PHPQuantidade de visualizações: 1398 vezes |
|
Todos estamos acostumados com o Teorema de Pitágoras, que diz que "o quadrado da hipotenusa é igual à soma dos quadrados dos catetos". Baseado nessa informação, fica fácil retornar a medida do cateto oposto quando temos as medidas da hipotenusa e do cateto adjascente. Isso, claro, via programação em linguagem PHP. Comece observando a imagem a seguir:  Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. A medida da hipotenusa é, sem arredondamentos, 36.056 metros. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras): \[c^2 = a^2 + b^2\] Tudo que temos que fazer é mudar a fórmula para: \[a^2 = c^2 - b^2\] Veja que agora o quadrado do cateto oposto é igual ao quadrado da hipotenusa menos o quadrado do cateto adjascente. Não se esqueça de que a hipotenusa é o maior lado do triângulo retângulo. Veja agora como esse cálculo é feito em linguagem PHP: <?php $c = 36.056; // medida da hipotenusa $b = 30; // medida do cateto adjascente // agora vamos calcular o comprimento da cateto oposto $a = sqrt(pow($c, 2) - pow($b, 2)); // e mostramos o resultado echo "A medida do cateto oposto é: " . $a; ?> Ao executar este código PHP nós teremos o seguinte resultado: A medida do cateto oposto é: 20.000878380711 Como podemos ver, o resultado retornado com o código PHP confere com os valores da imagem apresentada. |
C ::: Dicas & Truques ::: Data e Hora |
Como usar o tipo time_t do header <time.h> da linguagem CQuantidade de visualizações: 5225 vezes |
O tipo time_t, presente no header <time.h> é usado quando precisamos representar datas e horas e, quando necessário, efetuar operações aritméticas envolvendo as mesmas. Este tipo é obtido por meio de uma chamada à função time(). Veja:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(int argc, char *argv[]){
// declara uma variável do tipo time_t e atribui a ela
// o resultado de uma chamada à função time()
time_t hora_atual = time(NULL);
printf("Segundos desde 01/01/1970: %d\n\n", hora_atual);
system("PAUSE");
return 0;
}
Ao executar este trecho de código teremos algo parecido com: Segundos desde 01/01/1970: 1334017044 Como podemos ver, o tipo time_t é apenas um apelido para um long, como declarado no header time.h: typedef long time_t; Desta forma, time_t guarda a quantidade de segundos decorridos desde a meia-noite do dia 01/01/1970 UTC. |
Portugol ::: Desafios e Lista de Exercícios Resolvidos ::: Laços de Repetição |
Exercício Resolvido de Portugol - Calculando e exibindo os números primos entre 2 e 100Quantidade de visualizações: 219 vezes |
|
Pergunta/Tarefa: Um inteiro é um número primo se ele for divisível somente por 1 e por ele mesmo. Assim, 2, 3, 5 e 7 são primos, enquanto 4, 6, 8 e 9 não são. Note que o número 1 não é primo. Escreva um programa (algorítmo) Portugol Web Studio que usa um laço PARA, ENQUANTO ou FACA...ENQUANTO para calcular e exibir os números primos entre 2 (incluindo) e 100 (incluindo). Sua saída deverá ser parecida com: Numeros primos entre 2 e 100: 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 Veja a resolução comentada deste exercício usando Portugol Web Studio:
programa {
funcao inicio() {
// limite dos números primos (incluindo)
inteiro limite = 100
logico primo
// Lembre-se! O número 1 não é primo
escreva("Numeros primos entre 2 e " + limite + ":\n")
// laço que percorre os valores de 2 até o limite desejado
para (inteiro i = 2; i <= limite; i++) {
primo = verdadeiro
// se o valor de i for 7, a variável j do laço contará
// de 2 até 7 / 2 (divisão inteira), ou seja, 3. Se o
// módulo de 7 por qualquer um dos valores neste intervalo
// for igual a 0, então o número não é primo
para (inteiro j = 2; j <= (i / 2); j++) {
se (i % j == 0) {
primo = falso // não é primo
pare
}
}
se (primo == verdadeiro) {
escreva(i, " ")
}
}
}
}
|
PHP ::: Dicas & Truques ::: Gráficos e Cores |
Gráficos em PHP - Como verificar se a extensão GD está disponível na sua instalação do PHPQuantidade de visualizações: 10491 vezes |
|
Gráficos em PHP são gerados a partir da biblioteca (ou extensão) GD. É claro que você pode usar outras bibliotecas, mas esta é a mais comumente usada e disponível nas hospedagens compartilhadas. Antes de começar a gerar gráficos e imagens, porém, você precisa verificar se a GD está disponível no seu interpretador. A melhor forma de verificar isso é usar a página phpinfo() e procurar a seção "GD". Você deverá ter algo assim: GD Support enabled GD Version 2.0 or higher FreeType Support enabled FreeType Linkage with freetype JPG Support enabled PNG Support enabled WBMP Support enabled A partir da versão 4.3 do PHP, uma versão da GD (equivalente à GD 2.0 ou mais recente) já vem instalada por padrão. Isso dispensa a instalação da biblioteca. |
JavaScript ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como testar se todos os elementos de um array satisfazem uma condição em JavaScript usando a função every()Quantidade de visualizações: 1559 vezes |
|
Em algumas situações nós gostaríamos de testar todos os elementos de um vetor e verificar se todos eles passam em um determinado teste. Para isso podemos usar a função every(), adicionada à linguagem JavaScript por meio do ECMAScript 5 (JavaScript 5, ECMAScript 2009, ES5). Este método nos permite fornecer uma função de callback que será chamada para cada um dos elementos do vetor. E o retorno do método every() é um valor true se todos os elementos passarem no teste e false em caso contrário. Veja um exemplo no qual testamos se TODOS os elementos de um vetor são maiores que 10:
<script type="text/javascript">
function testarTodos(valor, indice, vetor){
if(valor > 10){
return true;
}
}
var valores = new Array(21, 50, 30, 70, 12, 3);
// vamos verificar se TODOS os valores são
// maiores que 10
var res = valores.every(testarTodos);
window.alert("Todos passaram no teste: " + res);
</script>
Aqui o resultado será false, pois o valor 3 não passou no teste. É importante observar que, assim que a função de callback retorna false pela primeira vez, o método every() já abandona sua execução. Uma função passada para o método every() pode conter os seguintes argumentos (nessa mesma ordem): a) O valor do item; b) O índice do item (opcional); c) O vetor a partir do qual o método every() está sendo chamado (opcional). Como última observação, o método every() não modifica o array original. |
Java ::: Java para Engenharia ::: Eletricidade, Circuitos Elétricos e Eletrônicos |
Como calcular corrente, voltagem, resistência e potência em um circuito série de corrente contínua usando JavaQuantidade de visualizações: 1970 vezes |
|
Como calcular corrente, voltagem, resistência e potência em um círcuito série de corrente contínua usando Java Nesta dica mostrarei como é possível usar operações básicas da linguagem Java para calcular a corrente, voltagem, resistência e potência em um circuito série de corrente contínua. É conhecido como um circuito série um circuito composto exclusivamente por componentes elétricos ou eletrônicos conectados em série (de conexão em série, que é o mesmo que associação em série ou ligação em série). A associação em série é uma das formas básicas de se conectarem componentes elétricos ou eletrônicos. A nomeação descreve o método como os componentes são conectados. Vanos começar analisando a seguinte imagem: 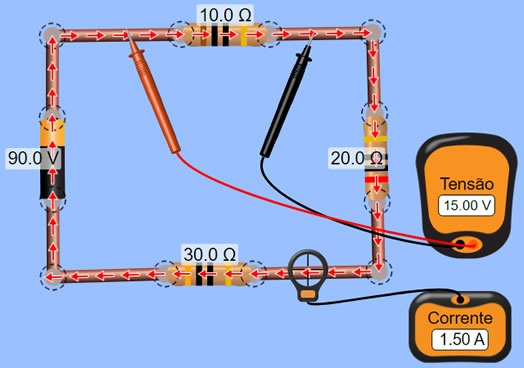 Esta imagem foi extraída do Simulador do PHET, no endereço https://phet.colorado.edu. Note que temos uma fonte de alimentação 90V, e três resistores (com resistências de 10Ω, 20Ω e 30Ω). Vamos começar relembrando os aspectos importantes dos circuitos em série: 1) A corrente elétrica I (medida em ampères (A), ou coulombs por segundo) é comum a todos os elementos do circuito. 2) A tensão elétrica V, (medida em volts (V), ou joules por coulomb) é dividida entre as cargas, ou seja, a soma das tensões nas cargas deve ser igual à tensão da fonte de alimentação. 3) A resistência elétrica R (medida em ohms (Ω)) total do circuito é igual à soma de todas as resistências das cargas. 4) A potência total P (medida em watts (W)) é igual à soma das potências das cargas que compõem o circuito. Vamos escrever um pouco de código então? Veja nosso primeiro código Java que calcula a corrente total, a tensão total, a resistência total e a potência total do circuito em série mostrado na imagem:
package estudos_java;
public class Estudos{
public static void main(String[] args){
// Tensão total do circuito em série
double eTotal = 90.0;
// Resitência total
double resist1 = 10.0;
double resist2 = 20.0;
double resist3 = 30.0;
double rTotal = resist1 + resist2 + resist3;
// Corrente elétrica total
double iTotal = eTotal / rTotal;
// Potência elétrica total
double pTotal = eTotal * iTotal;
// mostra os valores
System.out.println("Tensão total: " + eTotal);
System.out.println("Resistência total: " + rTotal);
System.out.println("Corrente total: " + iTotal);
System.out.println("Potência total: " + pTotal);
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Tensão total: 90.0 Resistência total: 60.0 Corrente total: 1.5 Potência total: 135.0 Pronto! Agora que já sabemos o valor da corrente elétrica, e sabemos que a corrente é comum a todos os elementos do circuito em série, podemos calcular a tensão individual dos componentes. Assim, veja um trecho de código Java que calcula a tensão elétrica nos três resistores (lembre-se: tensão é o produto da corrente pela resistência):
package estudos_java;
public class Estudos{
public static void main(String[] args){
// Tensão total do circuito em série
double eTotal = 90.0;
// Resitência total
double resist1 = 10.0;
double resist2 = 20.0;
double resist3 = 30.0;
double rTotal = resist1 + resist2 + resist3;
// Corrente elétrica total
double iTotal = eTotal / rTotal;
// Potência elétrica total
double pTotal = eTotal * iTotal;
// mostra os valores
System.out.println("Tensão total: " + eTotal);
System.out.println("Resistência total: " + rTotal);
System.out.println("Corrente total: " + iTotal);
System.out.println("Potência total: " + pTotal);
// mostra as tensões nos resistores
System.out.println("\nTensão nos resistores individuais:");
double e1 = resist1 * iTotal;
double e2 = resist2 * iTotal;
double e3 = resist3 * iTotal;
System.out.println("Tensão no Resistor 1: " + e1 + "V");
System.out.println("Tensão no Resistor 2: " + e2 + "V");
System.out.println("Tensão no Resistor 3: " + e3 + "V");
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Tensão total: 90.0 Resistência total: 60.0 Corrente total: 1.5 Potência total: 135.0 Tensão nos resistores individuais: Tensão no Resistor 1: 15.0V Tensão no Resistor 2: 30.0V Tensão no Resistor 3: 45.0V Para finalizar, vamos calcular a potência dissipada em cada um dos resistores de forma individual. Observe que a potência é o produto da tensão pela corrente (P = E.I). Eis o código:
package estudos_java;
public class Estudos{
public static void main(String[] args){
// Tensão total do circuito em série
double eTotal = 90.0;
// Resitência total
double resist1 = 10.0;
double resist2 = 20.0;
double resist3 = 30.0;
double rTotal = resist1 + resist2 + resist3;
// Corrente elétrica total
double iTotal = eTotal / rTotal;
// Potência elétrica total
double pTotal = eTotal * iTotal;
// mostra os valores
System.out.println("Tensão total: " + eTotal);
System.out.println("Resistência total: " + rTotal);
System.out.println("Corrente total: " + iTotal);
System.out.println("Potência total: " + pTotal);
// mostra as tensões nos resistores
System.out.println("\nTensão nos resistores individuais:");
double e1 = resist1 * iTotal;
double e2 = resist2 * iTotal;
double e3 = resist3 * iTotal;
System.out.println("Tensão no Resistor 1: " + e1 + "V");
System.out.println("Tensão no Resistor 2: " + e2 + "V");
System.out.println("Tensão no Resistor 3: " + e3 + "V");
// mostra as potências dissapadas nos resistores
System.out.println("\nPotência dissipada nos resistores individuais:");
double p1 = e1 * iTotal; // Potência = Tensão x Corrente
double p2 = e2 * iTotal;
double p3 = e3 * iTotal;
System.out.println("Potência no Resistor 1: " + p1 + "W");
System.out.println("Potência no Resistor 2: " + p2 + "W");
System.out.println("Potência no Resistor 3: " + p3 + "W");
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Tensão total: 90.0 Resistência total: 60.0 Corrente total: 1.5 Potência total: 135.0 Tensão nos resistores individuais: Tensão no Resistor 1: 15.0V Tensão no Resistor 2: 30.0V Tensão no Resistor 3: 45.0V Potência dissipada nos resistores individuais: Potência no Resistor 1: 22.5W Potência no Resistor 2: 45.0W Potência no Resistor 3: 67.5W |
Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como somar os elementos da diagonal principal de uma matriz em PythonQuantidade de visualizações: 3699 vezes |
|
A Matriz quadrada é um tipo especial de matriz que possui o mesmo número de linhas e o mesmo número de colunas, ou seja, dada uma matriz Anxm, ela será uma matriz quadrada se, e somente se, n = m, onde n é o número de linhas e m é o número de colunas. Em geral as matrizes quadradas são chamadas de Matrizes de Ordem n, onde n é o número de linhas e colunas. Dessa forma, uma matriz de ordem 4 é uma matriz que possui 4 linhas e quatro colunas. Toda matriz quadrada possui duas diagonais, e elas são muito exploradas tanto na matemática quanto na construção de algorítmos. Essas duas diagonais são chamadas de Diagonal Principal e Diagonal Secundária. A diagonal principal de uma matriz quadrada une o seu canto superior esquerdo ao canto inferior direito. Veja: 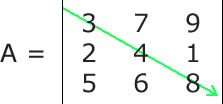 Nesta dica veremos como calcular a soma dos valores dos elementos da diagonal principal de uma matriz usando Python. Para isso, só precisamos manter em mente que a diagonal principal de uma matriz A é a coleção das entradas Aij em que i é igual a j. Assim, tudo que temos a fazer é converter essa regra para código Python. Veja um trecho de código Python completo no qual pedimos para o usuário informar os elementos da matriz e em seguida mostramos a soma dos elementos da diagonal superior:
def main():
# vamos declarar e construir uma matriz de três linhas
# e três colunas
linhas, colunas = (3, 3)
matriz = [[0 for x in range(linhas)] for y in range(colunas)]
soma_diagonal = 0 # guarda a soma dos elementos na diagonal
# principal
# vamos ler os elementos da matriz
for i in range(len(matriz)):
for j in range(len(matriz[i])):
matriz[i][j] = int(input("Informe o valor para a linha " + str(i)
+ " e coluna " + str(j) + ": "))
print()
for i in range(len(matriz)):
for j in range(len(matriz[i])):
print(matriz[i][j], end=' ')
print()
# vamos calcular a soma dos elementos da diagonal
# principal
for i in range(len(matriz)):
for j in range(len(matriz[i])):
if i == j:
soma_diagonal = soma_diagonal + matriz[i][j]
# finalmente mostramos a soma da diagonal principal
print("\nA soma dos elementos da diagonal principal é: %d" %
soma_diagonal)
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Informe o valor para a linha 0 e coluna 0: 3 Informe o valor para a linha 0 e coluna 1: 7 Informe o valor para a linha 0 e coluna 2: 9 Informe o valor para a linha 1 e coluna 0: 2 Informe o valor para a linha 1 e coluna 1: 4 Informe o valor para a linha 1 e coluna 2: 1 Informe o valor para a linha 2 e coluna 0: 5 Informe o valor para a linha 2 e coluna 1: 6 Informe o valor para a linha 2 e coluna 2: 8 3 7 9 2 4 1 5 6 8 A soma dos elementos da diagonal principal é: 15 |
Nossas 20 dicas & truques de programação mais populares |
|
Java - Como carregar uma imagem em um BufferedImage do Java usando o método read() da classe ImageIO Delphi - Como selecionar um item de uma ListBox do Delphi em tempo de execução usando a propriedade ItemIndex Java - Como converter Coordenadas Cartesianas para Coordenadas Polares usando Java - Java para Engenharia |
Você também poderá gostar das dicas e truques de programação abaixo |
|
QGIS - Como retornar o título do projeto do QGIS usando PyQGIS e a função title() da classe QgsProject CSS - Como definir uma imagem de fundo para a página HTML em CSS usando a propriedade background-image |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






