VB.NET ::: Dicas & Truques ::: Strings e Caracteres |
Como comparar strings em VB.NET usando o método Compare() da classe String do .NET FrameworkQuantidade de visualizações: 12433 vezes |
|
Este exemplo mostra como comparar strings em VB.NET usando o método Compare() da classe String. Lembre-se de que a versão do método que usamos neste exemplo diferencia maiúsculas de minúsculas. Veja o código completo:
Imports System
Module Program
Sub Main(args As String())
Dim palavra1, palavra2 As String
palavra1 = "Visual Basic"
palavra2 = "Visual Basic"
If String.Compare(palavra1, palavra2) = 0 Then
Console.WriteLine("As duas strings são iguais")
Else
Console.WriteLine("As duas strings são diferentes")
End If
Console.WriteLine(vbCrLf & "Pressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código VB.NET nós teremos o seguinte resultado: As duas strings são iguais |
C++ ::: C++ para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como somar os elementos da diagonal principal de uma matriz em C++Quantidade de visualizações: 1550 vezes |
|
A Matriz quadrada é um tipo especial de matriz que possui o mesmo número de linhas e o mesmo número de colunas, ou seja, dada uma matriz Anxm, ela será uma matriz quadrada se, e somente se, n = m, onde n é o número de linhas e m é o número de colunas. Em geral as matrizes quadradas são chamadas de Matrizes de Ordem n, onde n é o número de linhas e colunas. Dessa forma, uma matriz de ordem 4 é uma matriz que possui 4 linhas e quatro colunas. Toda matriz quadrada possui duas diagonais, e elas são muito exploradas tanto na matemática quanto na construção de algorítmos. Essas duas diagonais são chamadas de Diagonal Principal e Diagonal Secundária. A diagonal principal de uma matriz quadrada une o seu canto superior esquerdo ao canto inferior direito. Veja: 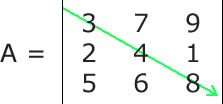 Nesta dica veremos como calcular a soma dos valores dos elementos da diagonal principal de uma matriz usando C++. Para isso, só precisamos manter em mente que a diagonal principal de uma matriz A é a coleção das entradas Aij em que i é igual a j. Assim, tudo que temos a fazer é converter essa regra para código C++. Veja um trecho de código C++ completo no qual pedimos para o usuário informar os elementos da matriz e em seguida mostramos a soma dos elementos da diagonal superior:
#include <iostream>
#include <cstdlib>
using namespace std;
int main(int argc, char *argv[]){
// vamos declarar e construir uma matriz de três linhas
// e três colunas
int linhas = 3, colunas = 3;
int matriz[linhas][colunas];
// guarda a soma dos elementos na diagonal principal
int soma_diagonal = 0;
// vamos ler os valores para os elementos da matriz
for(int i = 0; i < linhas; i++){ // linhas
for(int j = 0; j < colunas; j++){ // colunas
cout << "Informe o valor para a linha " << i <<
" e coluna " << j << ": ";
cin >> matriz[i][j];
}
}
// vamos mostrar a matriz da forma que ela
// foi informada
cout << "\n";
// percorre as linhas
for(int i = 0; i < linhas; i++){
// percorre as colunas
for(int j = 0; j < colunas; j++){
cout << matriz[i][j] << " ";
}
// passa para a próxima linha da matriz
cout << "\n";
}
// vamos calcular a soma dos elementos da diagonal
// principal
for(int i = 0; i < linhas; i++){
for(int j = 0; j < colunas; j++){
if(i == j){
soma_diagonal = soma_diagonal + matriz[i][j];
}
}
}
// finalmente mostramos a soma da diagonal principal
cout << "\nA soma dos elementos da diagonal principal é: "
<< soma_diagonal << "\n\n";
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
Ao executar este código C++ nós teremos o seguinte resultado: Informe o valor para a linha 0 e coluna 0: 3 Informe o valor para a linha 0 e coluna 1: 7 Informe o valor para a linha 0 e coluna 2: 9 Informe o valor para a linha 1 e coluna 0: 2 Informe o valor para a linha 1 e coluna 1: 4 Informe o valor para a linha 1 e coluna 2: 1 Informe o valor para a linha 2 e coluna 0: 5 Informe o valor para a linha 2 e coluna 1: 6 Informe o valor para a linha 2 e coluna 2: 8 3 7 9 2 4 1 5 6 8 A soma dos elementos da diagonal principal é: 15 |
Java ::: Dicas & Truques ::: Strings e Caracteres |
Como converter uma string para letras maiúsculas em Java - Como transformar uma string em maiúsculas usando o método toUpperCase() da classe StringQuantidade de visualizações: 338 vezes |
|
A classe String nos fornece o toUpperCase() que converte todas as letras em um texto para letras maiúsculas e nos retorna o resultado de acordo com o locale padrão. Este método é semelhante à toUpperCase(Locale.getDefault()). Veja um exemplo de como transformar todas as letras de uma frase para letras maiúsculas:
package arquivodecodigos;
public class Estudos{
public static void main(String[] args){
String original = "Onde posso aprender a programar em Java?";
// vamos convertar para letras maísculas
String maiusculas = original.toUpperCase();
// vamos mostrar o resultado
System.out.println("String original: " + original);
System.out.println("Em letras maiúsculas: " + maiusculas);
System.exit(0);
}
}
Ao executarmos este código nós teremos o seguinte resultado: String original: Onde posso aprender a programar em Java? Em letras maiúsculas: ONDE POSSO APRENDER A PROGRAMAR EM JAVA? Esta dica foi revisada e atualizada para o Java 8. |
C ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como converter radianos em graus na linguagem CQuantidade de visualizações: 5679 vezes |
|
Todos os métodos e funções trigonométricas em C recebem seus argumentos em radianos, em vez de graus. Um exemplo disso é a função sin() do header math.h. Esta função recebe o ângulo em radianos e retorna o seu seno. No entanto, há momentos nos quais precisamos retornar alguns valores como graus. Para isso é importante sabermos fazer a conversão de radianos para graus. Veja a fórmula abaixo: \[Graus = Radianos \times \frac{180}{\pi}\] Agora veja como esta fórmula pode ser escrita em código C:
#include <stdio.h>
#include <stdlib.h>
// vamos definir o valor de PI
#define PI 3.14159265358979323846
int main(int argc, char *argv[]){
// valor em radianos
double radianos = 1.5;
// obtém o valor em graus
double graus = radianos * (180 / PI);
// mostra o resultado
printf("%f radianos convertidos para graus é %f\n\n",
radianos, graus);
system("PAUSE");
return 0;
}
Ao executarmos este código C nós teremos o seguinte resultado: 1.500000 radianos convertidos para graus é 85.943669 Para fins de memorização, 1 radiano equivale a 57,2957795 graus. |
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Strings e Caracteres |
Exercício Resolvido de Python - Como testar se duas palavras são anagramas uma da outra - Solução usando dicionário/hash tableQuantidade de visualizações: 2560 vezes |
|
Exercícios Resolvidos de Python - Como testar se duas palavras são anagramas uma da outra - Solução usando dicionário/hash table Pergunta/Tarefa: Dadas duas palavras p1 e p2, escreva um código Python que informa se uma palavra é anagrama da outra. Um anagrama é uma espécie de jogo de palavras criado com a reorganização das letras de uma palavra ou expressão para produzir outras palavras ou expressões, utilizando todas as letras originais exatamente uma vez. Para esta solução você deverá, obrigatoriamente, usar um dicionário Python, ou seja, um objeto dict. O objetivo é construir duas tabelas de frequências dos caracteres de cada palavra. Dicionários em Python são similares às tabelas hash (hash tables) em outras linguagens de programação. Seu programa deverá exibir a seguinte saída:  Resposta/Solução: Veja a resolução com código comentado em Python:
# método que recebe duas palavras e retorna
# verdadeiro se uma palavra for anagrama da
# outra
def anagramas(palavra1, palavra2):
# o primeiro passo é verificar se os comprimentos das duas
# palavras são iguais
if(len(palavra1) != len(palavra2)):
return False
# agora criamos dois dictionaries para as frequencias de
# cada uma das palavras
freq_p1 = {}
freq_p2 = {}
# agora registramos as frequências de letras na primeira
# palavra
for letra in palavra1:
# a letra já está no dicionário?
if letra in freq_p1:
freq_p1[letra] += 1 # aumenta a frequêcia desta letra
else:
freq_p1[letra] = 1 # ainda não estava no dicionário
# agora registramos as frequências de letras na segunda
# palavra
for letra in palavra2:
# a letra já está no dicionário?
if letra in freq_p2:
freq_p2[letra] += 1 # aumenta a frequêcia desta letra
else:
freq_p2[letra] = 1 # ainda não estava no dicionário
# registradas as frequências de letras das duas palavras,
# chegou a hora de compararmos os dois dicionários
for chave in freq_p1:
# esta chave não está no segundo dicionário ou
# possui valores diferentes?
if chave not in freq_p2 or freq_p1[chave] != freq_p2[chave]:
return False
# se chegou até aqui então uma palavra é anagrama da outra
return True
def main():
# vamos ler duas palavras e verificar se uma é anagrama da outra
palavra1 = input("Informe a primeira palavra: ")
palavra2 = input("Informe a segunda palavra: ")
# vamos chamar o método que faz a verificação
if(anagramas(palavra1, palavra2)):
print("As duas palavras são anagramas")
else:
print("As duas palavras não são anagramas")
if __name__== "__main__":
main()
|
Java ::: Reflection (introspecção) e RTI (Runtime Type Information) ::: Passos Iniciais |
Como retornar o nome de uma classe Java usando os métodos getClass() e getName()Quantidade de visualizações: 13563 vezes |
|
Entre os métodos que uma classe herda da classe Object, está o método getClass(). Este método retorna um objeto da classe Class e podemos tirar proveito disso para fazer em encadeamento e chamar também o método getName() para obter o nome de uma determinada classe. Veja o exemplo no qual obtemos uma String contendo o nome de uma classe (juntamente com o nome do pacote ao qual ela pertence):
import javax.swing.*;
public class Estudos{
public static void main(String args[]){
JButton btn = new JButton();
String nomeClasse = btn.getClass().getName();
System.out.println(nomeClasse);
// exibirá: "javax.swing.JButton"
System.exit(0);
}
}
Ao executarmos este código nós teremos o seguinte resultado: javax.swing.JButton |
jQuery ::: Dicas & Truques ::: Manipulação e Conteúdo Dinâmico |
Como usar o método prependTo() do jQuery para adicionar todo o conteúdo de um elemento ao final de outro elemento HTMLQuantidade de visualizações: 7365 vezes |
|
O método prependTo() é usado quando queremos adicionar todo o conteúdo dos elementos retornados sob uma determinada condição no início de outro ou outros elementos HTML. Veja um trecho de código no qual adicionamos o conteúdo de um parágrafo no início de um elemento DIV:
<script type="text/javascript">
<!--
function adicionarConteudo(){
var texto = "Mais uma linha.<br>";
$("#parag").prependTo("#div_1");
}
//-->
</script>
O método prependTo() opera em todos os elementos HTML retornados sob uma determinação condição. O retorno do método é um objeto jQuery que pode ser usado para fins de encadeamento de chamadas de métodos. |
Portugol ::: Dicas & Truques ::: Matemática e Estatística |
Como resolver uma equação do segundo grau em Portugol - Como calcular Bhaskara em PortugolQuantidade de visualizações: 2615 vezes |
|
Como resolver uma equação do 2º grau usando Portugol Nesta dica mostrarei como encontrar as raízes de uma equação quadrática, ou seja, uma equação do 2º usando um algoritmo escrito na ferramenta Portugol Studio, uma das preferidas para o aprendizado de algoritmos e lógica de programação. Definimos como equação do 2º grau ou equações quadráticas qualquer equação do tipo ax² + bx + c = 0 em que a, b e c são números reais e a ≠ 0. Ela recebe esse nome porque, no primeiro membro da igualdade, há um polinômio de grau dois com uma única incógnita. Note que, dos coeficientes a, b e c, somente o a é diferente de zero, pois, caso ele fosse igual a zero, o termo ax² seria igual a zero, logo a equação se tornaria uma equação do primeiro grau: bx + c = 0. Independentemente da ordem da equação, o coeficiente a sempre acompanha o termo x², o coeficiente b sempre acompanha o termo x, e o coeficiente c é sempre o termo independente. Como resolver uma equação do 2º grau Conhecemos como soluções ou raízes da equação ax² + bx + c = 0 os valores de x que fazem com que essa equação seja verdadeira. Uma equação do 2º grau pode ter no máximo dois números reais que sejam raízes dela. Para resolver equações do 2º grau completas, existem dois métodos mais comuns: a) Fórmula de Bhaskara; b) Soma e produto. O primeiro método é bastante mecânico, o que faz com que muitos o prefiram. Já para utilizar o segundo, é necessário o conhecimento de múltiplos e divisores. Além disso, quando as soluções da equação são números quebrados, soma e produto não é uma alternativa boa. Como resolver uma equação do 2º grau usando Bhaskara Como nosso algoritmo Portugol vai resolver a equação quadrática usando a Fórmula de Bhaskara, o primeiro passo é encontrar o determinante. Veja: \[\Delta =b^2-4ac\] Nem sempre a equação possui solução real. O valor do determinante é que nos indica isso, existindo três possibilidades: a) Se determinante > 0, então a equação possui duas soluções reais. b) Se determinante = 0, então a equação possui uma única solução real. c) Se determinante < 0, então a equação não possui solução real. Encontrado o determinante, só precisamos substituir os valores, incluindo o determinante, na Fórmula de Bhaskara: \[x = \dfrac{- b\pm\sqrt{b^2- 4ac}}{2a}\] Vamos agora ao código Portugol (escrevi e testei no Portugol Webstudio). Nossa aplicação vai pedir para o usuário informar os valores dos três coeficientes a, b e c e, em seguida, vai apresentar as raizes da equação:
// "Como resolver uma equação do 2º grau usando Portugol
programa {
// inclui a biblioteca Matematica
inclua biblioteca Matematica --> mat
// função principal do programa
funcao inicio() {
// variáveis usadas na resolução do problema
// os coeficientes
real a, b, c
// as duas raizes, a imaginaria e o discriminante
real raiz1, raiz2, imaginaria, discriminante
// vamos pedir para o usuário informar os valores dos coeficientes
escreva("Valor do coeficiente a: ")
leia(a)
escreva("Valor do coeficiente b: ")
leia(b)
escreva("Valor do coeficiente c: ")
leia(c)
// vamos calcular o discriminante
discriminante = (b * b) - (4 * a * c)
// a equação possui duas soluções reais?
se (discriminante > 0) {
raiz1 = ((b * -1) + mat.raiz(discriminante, 2.0)) / (2 * a)
raiz2 = ((b * -1) - mat.raiz(discriminante, 2.0)) / (2 * a)
escreva("Duas raizes: x1 = ", raiz1, " e x2 = ", raiz2)
}
// a equação possui uma única solução real?
senao se (discriminante == 0){
raiz1 = (b * -1) / (2 * a)
raiz2 = (b * -1) / (2 * a)
escreva("Duas raizes iguais: x1 = ", raiz1, " e x2 = ", raiz2)
}
// a equação não possui solução real?
senao{
raiz1 = (b * -1) / (2 * a)
raiz2 = (b * -1) / (2 * a)
imaginaria = mat.raiz((discriminante * -1), 2.0) / (2 * a)
escreva("Existem duas raízes complexas: ")
escreva("x1 = ", raiz1, " + " ,imaginaria, " e x2 = ", raiz2, " - ", imaginaria)
}
}
}
Ao executar este código Portugol nós teremos o seguinte resultado: Valor do coeficiente a: 1 Valor do coeficiente b: 2 Valor do coeficiente c: -3 Existem duas raizes: x1 = 1.0 e x2 = -3.0 |
C ::: C para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular a norma ou módulo de vetores nos espaços R2 e R3 usando C - Geometria Analítica e Álgebra Linear usando CQuantidade de visualizações: 4316 vezes |
|
Em Geometria Analítica e Álgebra Linear, a magnitude, norma, comprimento, tamanho ou módulo (também chamado de intensidade na Física) de um vetor é o seu comprimento, que pode ser calculado por meio da distância de seu ponto final a partir da origem, no nosso caso (0,0). Considere o seguinte vetor no plano, ou seja, no espaço bidimensional, ou R2: \[\vec{v} = \left(7, 6\right)\] Aqui este vetor se inicia na origem (0, 0) e vai até as coordenadas (x = 7) e (y = 6). Veja sua plotagem no plano 2D:  Note que na imagem já temos todas as informações que precisamos, ou seja, o tamanho desse vetor é 9 (arredondado) e ele faz um ângulo de 41º (graus) com o eixo x positivo. Em linguagem mais adequada da trigonometria, podemos dizer que a medida do cateto oposto é 6, a medida do cateto adjacente é 7 e a medida da hipotenusa (que já calculei para você) é 9. Note que já mostrei também o ângulo theta (__$\theta__$) entre a hipotenusa e o cateto adjacente, o que nos dá a inclinação da reta representada pelos pontos (0, 0) e (7, 6). Relembrando nossas aulas de trigonometria nos tempos do colegial, temos que o quadrado da hipotenusa é a soma dos quadrados dos catetos, ou seja, o Teorema de Pitágoras: \[a^2 = b^2 + c^2\] Como sabemos que a potenciação é o inverso da radiciação, podemos escrever essa fórmula da seguinte maneira: \[a = \sqrt{b^2 + c^2}\] Passando para os valores x e y que já temos: \[a = \sqrt{7^2 + 6^2}\] Podemos comprovar que o resultado é 9,21 (que arredondei para 9). Não se esqueça da notação de módulo ao apresentar o resultado final: \[\left|\vec{v}\right| = \sqrt{7^2 + 6^2}\] E aqui está o código C que nos permite informar os valores x e y do vetor e obter o seu comprimento, tamanho ou módulo:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(int argc, char *argv[]){
float x, y, norma;
// vamos ler os valores x e y
printf("Informe o valor de x: ");
scanf("%f", &x);
printf("Informe o valor de y: ");
scanf("%f", &y);
// vamos calcular a norma do vetor
norma = sqrt(pow(x, 2) + pow(y, 2));
// mostra o resultado
printf("A norma do vetor é: %f", norma);
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: Informe o valor de x: 7 Informe o valor de y: 6 A norma do vetor é: 9.219544457292887 Novamente note que arredondei o comprimento do vetor para melhor visualização no gráfico. Para calcular a norma de um vetor no espaço, ou seja, no R3, basta acrescentar o componente z no cálculo. |
Java ::: Design Patterns (Padrões de Projeto) ::: Singleton Pattern |
Padrões de projeto para iniciantes - Como usar o padrão de projeto Singleton em suas aplicações JavaQuantidade de visualizações: 12005 vezes |
|
O padrão de projeto Singleton (ou Singleton Pattern) é um dos padrões de projeto mais conhecidos e implementado extensivamente nas linguagens que suportam programação orientada a objetos, tais como Java e C#. Nesta dica eu mostrarei como implementá-lo. Uma das situações nas quais usamos o padrão Singleton é quando queremos que somente uma instância de uma determinada classe seja criada e que esta esteja disponível para todas as demais classes do sistema. Um exemplo disso é uma classe responsável por registrar logs do sistema, uma classe responsável por obter conexões com o banco de dados, ou ainda uma classe que concentra dados de configuração da aplicação. Assim, a chave do padrão Singleton é um método estático, geralmente chamado de getInstance(), que retorna uma nova instância da classe se esta ainda não foi instanciada. Se a classe já tiver sido instanciada, o método getInstance() retorna a instância já existente. Vamos ver um exemplo deste padrão em Java. Observe o código a seguir: Código para Logger.java:
package estudos;
// Uma classe Singleton responsável por gravar
// logs no sistema
public class Logger {
// variável estática e privada que guarda a instância
// atual da classe
private static Logger instancia = null;
// Método estático que retorna uma instância já existente, ou
// cria uma nova instância
public static Logger getInstance() {
if (instancia == null) {
instancia = new Logger();
}
return instancia;
}
// Construtor privado para evitar que instâncias sejam
// criadas usando new
private Logger() {
// não precisamos fazer nada aqui
}
// método usado para registrar logs
public void registrarLog(String dados) {
System.out.println("Vou registrar o log: " + dados);
}
}
Veja agora como podemos chamar o método getInstance(), obter um objeto da classe Logger e "registrar um log": Código para Main.java:
package estudos;
public class Main {
public static void main(String[] args) {
// vamos registrar um novo log usando a classe Singleton
Logger.getInstance().registrarLog("Novo usuário cadastrado.");
}
}
Ao executar esta aplicação teremos a seguinte saída: Vou registrar o log: Novo usuário cadastrado. |
Nossas 20 dicas & truques de programação mais populares |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






