 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de Java - Escreva um programa Java para mover todos os zeros para o final do vetor, sem alterar a ordem dos elementos já presentes no arrayQuantidade de visualizações: 713 vezes |
|
Pergunta/Tarefa: Dado o seguinte vetor de inteiros:
// vamos declarar e construir um vetor de 8 inteiros
int valores[] = {0, 3, 0, 5, 7, 4, 0, 9};
Sua saída deverá ser parecida com: Vetor na ordem original: 0 3 0 5 7 4 0 9 Vetor com os zeros deslocados para o final: 3 5 7 4 9 0 0 0 Veja a resolução comentada deste exercício usando Java:
package exercicio;
public class Exercicio {
public static void main(String[] args) {
// vamos declarar e construir um vetor de 8 inteiros
int valores[] = {0, 3, 0, 5, 7, 4, 0, 9};
// vamos mostrar o vetor na ordem original
System.out.println("Vetor na ordem original:\n");
for(int i = 0; i < valores.length; i++){
System.out.print(valores[i] + " ");
}
// vamos inicializar j como 0 para que ele aponte para
// o primeiro elemento do vetor
int j = 0;
// agora o laço for percorre todos os elementos do vetor,
// incrementanto a variável i e deixando o j em 0
for(int i = 0; i < valores.length; i++){
// encontramos um valor que não é 0
if(valores[i] != 0){
// fazemos a troca entre os elementos nos índices
// i e j
int temp = valores[i];
valores[i] = valores[j];
valores[j] = temp;
// e avançamos o j para o elemento seguinte
j++;
}
}
// agora mostramos o resultado
System.out.println("\n\nVetor com os zeros deslocados para o final:\n");
for(int i = 0; i < valores.length; i++){
System.out.print(valores[i] + " ");
}
System.out.println();
}
}
Não se esqueça: A resolução do exercício deve ser feita sem a criação de um vetor, array ou lista adicional, e os elementos diferentes de zero devem permanecer na mesma ordem que eles estavam antes. |
Ruby ::: Dicas & Truques ::: Data e Hora |
Datas e horas em Ruby: Time, Date ou DateTime - Qual classe devo usar?Quantidade de visualizações: 8698 vezes |
|
A linguagem Ruby oferece três classes básicas para lidar com datas e horas: Time, Date e DateTime. Para ajudá-lo em seus estudos, veja uma descrição breve de cada uma: 1) A classe Time está mais para um encapsulamento das funções de datas e horas da biblioteca C. Estas bibliotecas são geralmente baseadas na época UNIX (UNIX epoch) e, assim, não conseguem representar datas e horas antes de 1970. 2) A classe Date foi criada para superar estas deficiências da classe Time. Com esta classe nós podemos lidar com datas realmente antigas, tais como o aniversário de Leonardo da Vinci (15 de abril de 1452) e, esta classe funciona muito bem com a reforma do calendário. No entanto, a classe Date não permite lidar com horas, ou seja, ao usá-la não seremos capazes de representar a hora que Leonardo da Vinci nasceu. Apenas a data de nascimento. 3) A classe DateTime herda da Date e tenta ser o melhor de ambos os mundos. Com esta classe podemos representar datas da mesma forma que Date e horas da mesma forma que Time. Geralmente os desenvolvedores optam por esta classe, por considerá-la a forma mais correta de representar datas e horas. |
PHP ::: PHP + MySQL ::: MySQL Improved Extension (mysqli) |
Como estabelecer uma conexão PHP + MySQL no modo procedimental - Como se conectar ao banco MySQL usando PHP (modo procedural) usando mysqli_connect - Revisado)Quantidade de visualizações: 7304 vezes |
|
Nesta dica mostrarei como usar a função mysqli_connect da extensão mysqli para efetuar uma conexão PHP + MySQL usando o modo precedimental, ou seja, nada de programação orientada aqui, mas em outras dicas dessa seção você encontrará a forma de conexão orientada a objetos. Veja um trecho de código completo no qual nos conectamos ao banco de dados MySQL e exibimos uma mensagem indicando o sucesso da operação:
<?
// vamos efetuar a conexão com o banco
$conexao = mysqli_connect("localhost", "root",
"osmar1234", "estudos");
// conexão efetuada com sucesso?
if(mysqli_connect_errno()) {
echo "Não foi possível efetuar a conexão com o MySQL: "
. mysqli_connect_error();
// vamos sair daqui
exit();
}
else{
echo "Conexão efetuada com sucesso.";
// fecha a conexão
mysqli_close($conexao);
}
?>
Este trecho de código foi revisado e testado no PHP 8. |
AutoCAD .NET API C# ::: Dicas & Truques ::: Linha, Linhas, Comando LINE |
Como selecionar uma linha no AutoCAD e mostrar a equação da reta correspondente usando AutoCAD .NET C# APIQuantidade de visualizações: 573 vezes |
|
Em algumas situações nós queremos posicionar pontos ou outros desenhos em cima de uma linha, ou seja, em cima de uma reta. Uma das melhores formas de fazer isso é obtendo a equação reduzida da reta e usar as coordenadas x e y correspondentes. Nesta dica eu mostro como isso pode ser feito usando a AutoCAD .NET C# API. O primeiro passo é pedir para o usuário selecionar a linha na área de desenho do AutoCAD usando doc.Editor.GetEntity(). Em seguida nós obtemos as coordenadas iniciais e finais da linha usando as propriedades StartPoint e EndPoint do objeto AcadLine. Para finalizar nós calculamos a equação reduzida da reta e exibimos o resultado. Fique atento ao código que calcula o coeficiente angular e linear da reta. Considere o caso em que o coeficiente angular ou linear é igual a 0. Veja o código AutoCAD .NET API C# completo para o exemplo:
using System;
using Autodesk.AutoCAD.Runtime;
using Autodesk.AutoCAD.ApplicationServices;
using Autodesk.AutoCAD.DatabaseServices;
using Autodesk.AutoCAD.Geometry;
using Autodesk.AutoCAD.EditorInput;
[assembly: CommandClass(typeof(PluginEstudos.Class1))]
namespace PluginEstudos {
public class Class1 {
[CommandMethod("estudos")]
public void Estudos() {
// vamos obter o documento atual
Document doc = Application.DocumentManager.MdiActiveDocument;
// vamos obter a base de dados
Database db = doc.Database;
// opções da seleção
PromptEntityOptions opcoes = new
PromptEntityOptions("\nSelecione uma linha: ");
// obtemos o resultado da seleção
PromptEntityResult resultado = doc.Editor.GetEntity(opcoes);
// a seleção foi feita com sucesso
if (resultado.Status != PromptStatus.OK) {
Application.ShowAlertDialog("Nenhum elemento selecionado.");
return;
}
// obtemos o id do objeto selecionado
ObjectId id_objeto = resultado.ObjectId;
// iniciamos uma transação
using (Transaction trans = db.TransactionManager.StartTransaction()) {
BlockTable tabela_blocos;
BlockTableRecord reg_tabela_blocos;
// obtemos a entidade selecionada
Entity ent = trans.GetObject(id_objeto, OpenMode.ForWrite) as Entity;
// a entidade selecionada é uma linha
if (ent is Line) {
Line linha = ent as Line;
// vamos obter o ponto inicial da linha
Point3d ponto_inicial = linha.StartPoint;
// vamos obter o ponto final da linha
Point3d ponto_final = linha.EndPoint;
string sinal = "+";
// vamos calcular o coeficiente angular da reta
Double m = (ponto_final.Y - ponto_inicial.Y) / (ponto_final.X - ponto_inicial.X);
// vamos calcular o coeficiente linear
double n = ponto_inicial.Y - (m * ponto_inicial.X);
// coeficiente linear menor que zero? O sinal será negativo
if (n < 0) {
sinal = "-";
n = n * -1;
}
// abre o model space para escrita
tabela_blocos = trans.GetObject(db.BlockTableId,
OpenMode.ForRead) as BlockTable;
reg_tabela_blocos = trans.GetObject(tabela_blocos[BlockTableRecord.ModelSpace],
OpenMode.ForWrite) as BlockTableRecord;
// vamos calcular as coordenadas x e y do ponto médio que
// será usado para posicionar o texto
double x = (ponto_inicial.X + ponto_final.X) / 2;
double y = (ponto_inicial.Y + ponto_final.Y) / 2;
// criamos um novo texto
DBText texto = new DBText();
texto.TextString = "y = " + m.ToString("0.00") + "x"
+ " " + sinal + " " + n.ToString("0.00");
texto.SetDatabaseDefaults();
texto.Height = 5;
texto.Position = new Point3d(x, y - texto.Height, 0);
// adicionamos o texto no desenho
reg_tabela_blocos.AppendEntity(texto);
trans.AddNewlyCreatedDBObject(texto, true);
}
else {
Application.ShowAlertDialog("Você não selecionou uma linha.");
}
// salvamos a transação
trans.Commit();
}
}
}
}
Ao executar este código AutoCAD .NET C# API e selecionar uma linha nós teremos um resultado parecido com: Selecione uma linha [Usuário seleciona a linha] [Mostra a equação reduzida da reta como um texto posicionado no ponto médio da linha] Como forma de testar ainda mais o código, defina um valor para o x e experimente plotar um ponto na área de desenho do AutoCAD. Você verá que o ponto cai exatamente em cima da linha, ou seja, da reta que a representa. |
C# ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Vetores e matrizes em C# - Como ordenar um vetor de inteiros usando o método Sort() da classe Array do C#Quantidade de visualizações: 16842 vezes |
|
Nesta dica mostrarei como podemos usar o método Sort() da classe Array da linguagem C# para classificar um vetor de inteiros em ordem crescente. Note que o método Sort() é estático e modifica o conteúdo do array original. Veja o código completo para o exemplo:
using System;
namespace Estudos{
class Program{
static void Main(string[] args) {
// cria e inicializa um array de inteiros
int[] valores = { 4, 69, 1, 0, 17, 23, 14 };
Console.WriteLine("Ordem original:");
for (int i = 0; i < valores.Length; i++)
Console.WriteLine(valores[i]);
// ordena o array
Array.Sort(valores);
// exibe os elementos na ordem crescente
Console.WriteLine();
Console.WriteLine("Ordem crescente:");
for (int i = 0; i < valores.Length; i++)
Console.WriteLine(valores[i]);
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código nós teremos o seguinte resultado: Ordem original: 4 69 1 0 17 23 14 Ordem crescente: 0 1 4 14 17 23 69 |
VisuAlg ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em VisuAlg dados dois pontos no plano cartesianoQuantidade de visualizações: 643 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem VisuAlg que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
algoritmo "Calcular o coeficiente angular de uma reta em VisuAlg"
var
// coordenadas dos dois pontos
x1, y1, x2, y2: real
// guarda o coeficiente angular
m: real
inicio
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos calcular o coeficiente angular
m <- (y2 - y1) / (x2 - x1)
// mostramos o resultado
escreva("O coeficiente angular é: ", m)
fimalgoritmo
Ao executar este código VisuAlg nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.6666666666666666 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
algoritmo "Calcular o coeficiente angular de uma reta em VisuAlg"
var
// coordenadas dos dois pontos
x1, y1, x2, y2: real
// guarda os comprimentos dos catetos oposto e adjascente
cateto_oposto, cateto_adjascente: real
// guarda o ângulo tetha (em radianos) e a tangente
tetha, tangente: real
inicio
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos obter o comprimento do cateto oposto
cateto_oposto <- y2 - y1
// e agora o cateto adjascente
cateto_adjascente <- x2 - x1
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
tetha <- ArcTan(cateto_oposto / cateto_adjascente)
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
tangente <- Tan(tetha)
// mostramos o resultado
escreva("O coeficiente angular é: ", tangente)
fimalgoritmo
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
PHP ::: Sistemas Completos com Código Fonte ::: Projetos PHP com Código Fonte - Códigos Fonte PHP |
Calendário de Eventos em PHP e MySQL - Código fonte completo com opções de cadastrar, listar, excluir, editar e listar eventosQuantidade de visualizações: 10159 vezes |
|
Aprenda como criar um Calendário de Eventos completo em PHP e MySQL. Código-fonte completo e comentado para programadores de nível iniciante e médio. Sobre este projeto PHP e MySQL Que tal aprender ou aprimorar as suas técnicas de programação em PHP e MySQL desenvolvendo um Calendário de Eventos completo, com as opções de cadastrar, listar, excluir, alterar e listar os eventos. Veja na imagem abaixo a tela inicial do sistema: 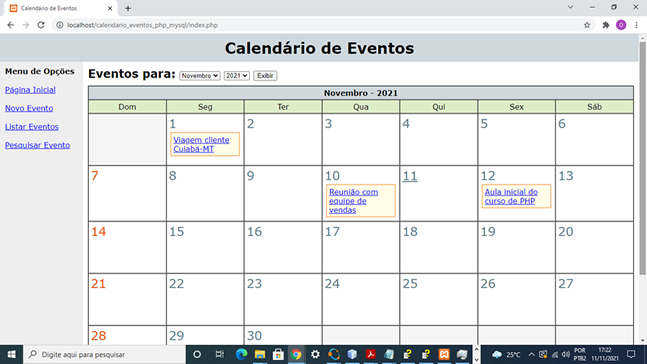 O que vou aprender neste código fonte? Além de aprender como gravar dados em uma tabela MySQL usando PHP, você verá, de forma prática e sem enrolação, como ler os dados de volta, editar, listar e pesquisar. Porém, o mais importante é que você aprenderá a construir um calendário usando PHP. Essa é uma técnica que você poderá levar para várias outras linguagens. Uma característica interessante deste código é o uso de uma janela modal feita usando apenas HTML e CSS. Essa janela é exibida por cima do calendário ao clicarmos em um determinado evento. Veja:  O código jQuery para exibir a janela é bem simples e poderá ser usado para várias outras aplicações. Além disso, o código para a requisição Ajax abrirá um mundo de possibilidades. Veja agora a tela para a criação de novos eventos: 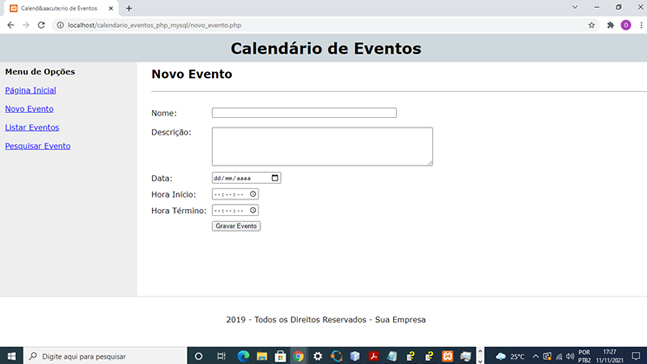 Para a construção desta tela de cadastro você aprenderá a usar os controles date e time do HTML5 para deixar seus códigos ainda mais robustos. Nesta tela você aprenderá também a validar os campos e exibir mensagens alertando ao usuário a necessidade do preenchimento correto. Para finalizar, veja a tela que lista todos os eventos cadastrados: 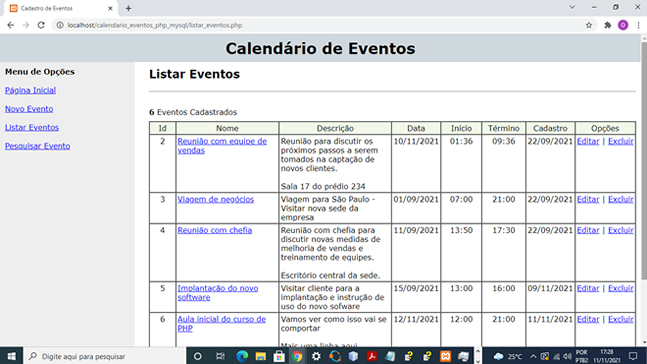 Nesta tela de listagem você aprenderá a colocar as opções para a visualização individual de cada evento assim como as opções de editar ou excluir os eventos. Como posso obter este código fonte? Para adquirir este código fonte, me chama no WhatsApp ou no e-mail indicados na lateral do site. Se necessário podemos combinar e faço a instalação na sua máquina ou no seu domínio. Podemos também combinar as alterações ou a adição de novas funcionalidades. |
Python ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o seno de um número ou ângulo em Python usando a função sin() do módulo MathQuantidade de visualizações: 1640 vezes |
|
Em geral, quando falamos de seno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função seno disponível nas linguagens de programação para calcular o seno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função seno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o seno é a razão entre o cateto oposto (oposto ao ângulo theta) e a hipotenusa, ou seja, o cateto oposto dividido pela hipotenusa. Veja a fórmula: \[\text{Seno} = \frac{\text{Cateto oposto}}{\text{Hipotenusa}} \] Então, se dividirmos 20 por 36.056 (na figura eu arredondei) nós teremos 0.5547, que é a razão entre o cateto oposto e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.5547. O resultado será 0.9828 (em radianos). Convertendo 0.9828 radianos para graus, nós obtemos 56.31º, que é exatamente o ângulo em graus entre o cateto oposto e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é seno na trigonometria, vamos entender mais sobre a função sin() da linguagem Python. Este método, que faz parte do módulo Math, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja:
# importamos a biblioteca Math
import math as math
def main():
print("Seno de 0 = ", math.sin(0))
print("Seno de 1 = ", math.sin(1))
print("Seno de 2 = ", math.sin(2))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Seno de 0 = 0.0 Seno de 1 = 0.8414709848078965 Seno de 2 = 0.9092974268256817 Note que calculamos os senos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função seno mostrada abaixo: 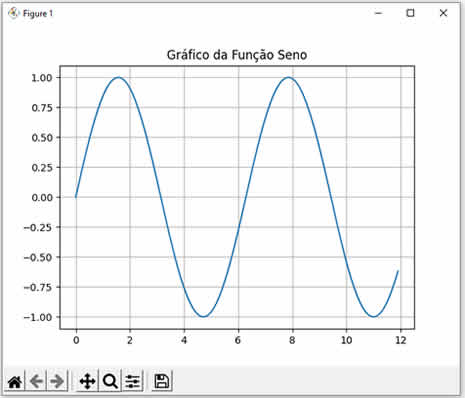 |
PHP ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de PHP - Escreva um programa PHP para mover todos os zeros para o final do vetor, sem alterar a ordem dos elementos já presentes no arrayQuantidade de visualizações: 1608 vezes |
|
Pergunta/Tarefa: Dado o seguinte vetor de inteiros: // vamos declarar e construir um vetor de 8 inteiros $valores = array(0, 3, 0, 5, 7, 4, 0, 9); Sua saída deverá ser parecida com: Vetor na ordem original: 0 3 0 5 7 4 0 9 Vetor com os zeros deslocados para o final: 3 5 7 4 9 0 0 0 Veja a resolução comentada deste exercício usando PHP:
<?php
// Este código PHP pode ser executado tanto na linha
// de comando quanto pelo servidor web
// vamos declarar e construir um vetor de 8 inteiros
$valores = array(0, 3, 0, 5, 7, 4, 0, 9);
// vamos mostrar o vetor na ordem original
echo("Vetor na ordem original:\n");
for($i = 0; $i < count($valores); $i++){
echo $valores[$i] . " ";
}
// vamos inicializar j como 0 para que ele aponte para
// o primeiro elemento do vetor
$j = 0;
// agora o laço for percorre todos os elementos do vetor,
// incrementanto a variável i e deixando o j em 0
for($i = 0; $i < count($valores); $i++){
// encontramos um valor que não é 0
if($valores[$i] != 0){
// fazemos a troca entre os elementos nos índices
// i e j
$temp = $valores[$i];
$valores[$i] = $valores[$j];
$valores[$j] = $temp;
// e avançamos o j para o elemento seguinte
$j++;
}
}
// agora mostramos o resultado
echo "\n\nVetor com os zeros deslocados para o final:\n";
for($i = 0; $i < count($valores); $i++){
echo $valores[$i] . " ";
}
?>
Não se esqueça: A resolução do exercício deve ser feita sem a criação de um vetor, array ou lista adicional, e os elementos diferentes de zero devem permanecer na mesma ordem que eles estavam antes. |
Delphi ::: VCL - Visual Component Library ::: TEdit |
Como obter a quantidade de caracteres em um TEdit do Delphi usando a função GetTextLen()Quantidade de visualizações: 12796 vezes |
|
Em algumas ocasiões nós precisamos descobrir a quantidade de caracteres contidos em uma caixa de texto do tipo TEdit. Para isso podemos usar o método GetTextLen(), definido originalmente na classe TControl. Esta função retorna um valor inteiro contendo o tamanho do texto da caixa de texto. Veja um exemplo do uso do método GetTextLen() no trecho de código a seguir:
procedure TForm1.Button1Click(Sender: TObject);
var
tamanho: Integer;
begin
// vamos obter a quantidade de caracteres no TEdit
tamanho := Edit1.GetTextLen();
// vamos mostrar o resultado
ShowMessage('O Edit contém ' + IntToStr(tamanho) + ' caracteres.');
end;
Ao executar este exemplo você terá um resultado parecido com: O Edit contém 5 caracteres. |
Nossas 20 dicas & truques de programação mais populares |
|
Python - Como definir o texto de um wx.Button do wxPython em tempo de execução usando a função SetLabel() JavaScript - JavaScript para iniciantes - Como usar o método escape() para codificar uma frase em JavaScript C - Como inverter (reverter) o conteúdo de uma string em C usando uma função str_reverse() personalizada |
Você também poderá gostar das dicas e truques de programação abaixo |
|
C - Como escrever uma função strtoupper() em C para transformar uma palavra inteira em letras maiúsculas Android Java - Como detectar um clique em um botão do Android usando o evento onClick no XML de layout AutoCAD Civil 3D .NET C# - Como retornar a quantidade de perfis de um alinhamento do Civil 3D usando a função GetProfileIds() da API C# do AutoCAD Civil 3D Python - Como calcular o coeficiente angular de uma reta em Python dados dois pontos no plano cartesiano |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





