 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
jQuery ::: Dicas & Truques ::: Manipulação e Conteúdo Dinâmico |
Como usar o método appendTo() do jQuery para adicionar todo o conteúdo de um elemento ao final de outro elemento HTMLQuantidade de visualizações: 557 vezes |
|
O método appendTo() é usado quando queremos adicionar todo o conteúdo dos elementos retornados sob uma determinada condição a outro ou outros elementos HTML. Veja um trecho de código no qual adicionamos o conteúdo de um parágrafo ao final de um elemento DIV:
<script type="text/javascript">
<!--
function adicionarConteudo(){
var texto = "<br>Mais uma linha.";
$("#parag").appendTo("#div_1");
}
//-->
</script>
O método appendTo() opera em todos os elementos HTML retornados sob uma determinação condição. O retorno do método é um objeto jQuery que pode ser usado para fins de encadeamento de chamadas de métodos. |
GoLang ::: Desafios e Lista de Exercícios Resolvidos ::: Geometria, Trigonometria e Figuras Geométricas |
Exercícios Resolvidos de Golang - Como calcular a área de um losango em GoQuantidade de visualizações: 1205 vezes |
|
Pergunta/Tarefa: Um losango é um quadrilátero equilátero, ou seja, é um polígono formado por quatro lados de igual comprimento. Um losango é também um paralelogramo. Alguns autores exigem ainda que nenhum dos ângulos do quadrilátero seja reto para que ele seja considerado um losango. A área (em metros quadrados) de um losango pode ser calculada usando-se a seguinte fórmula: 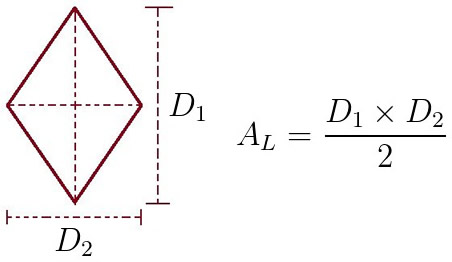 Onde D1 é a diagonal maior e D2 é a diagonal menor. Escreva um programa Golang que leia a diagonal maior e a diagonal menor e calcule a área do losango. Sua saída deverá ser parecida com: Informe a medida da diagonal maior: 5 Informe a medida da diagonal menor: 10 A área (em metros quadrados) do losango é: 25 Veja a resolução comentada deste exercício usando Go:
// pacote principal
package main
// vamos importar o módulo de formatação de
// entrada e saída
import "fmt"
// esta é a função principal do programa
func main() {
// variáveis que vamos usar na resolução do problema
var diagonal_maior, diagonal_menor int
var area float32
// vamos ler os valores das diagonais maior e menor
fmt.Print("Informe a medida da diagonal maior: ")
fmt.Scanln(&diagonal_maior)
fmt.Print("Informe a medida da diagonal menor: ")
fmt.Scanln(&diagonal_menor)
// calcula a area do losango
area = float32((diagonal_maior * diagonal_menor)) / 2
// mostra o resultado
fmt.Printf("A área (em metros quadrados) é: %.2f",
area)
}
|
Delphi ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Delphi para iniciantes: Como usar o laço de repetição for do DelphiQuantidade de visualizações: 22490 vezes |
|
O laço for do Delphi (linguagem Object Pascal) é usado quando queremos que um determinado bloco de instruções seja executado um determinado número de vezes. Na maioria das vezes a execução deste laço é controlada por uma variável de controle, que deve ser declarada antes de seu uso. Veja um laço for que contará de 0 até 10 (incluído):
procedure TForm1.Button3Click(Sender: TObject);
var
i: Integer; // variável de controle
begin
for i := 0 to 10 do
begin
ShowMessage(IntToStr(i)); // mostra a mensagem 10 vezes
end;
end;
Veja que o valor da variável de controle i começa em 0 e é incrementado a cada iteração até que seu valor seja igual a 10, o que faz com que a execução do laço seja interrompida. A variável de controle de um laço for deve ser do tipo ordinal (inteiro, caractere, Boolean, enumerações ou sub-faixas) e não pode ser alterada dentro do laço. Veja:
procedure TForm1.Button3Click(Sender: TObject);
var
i: Integer; // variável de controle
begin
// este laço for pretende exibir os números pares de 0 a 10
for i := 0 to 10 do
begin
ShowMessage(IntToStr(i));
i := i + 2; // vamos ter problemas aqui
end;
end;
Ao tentarmos compilar este código teremos o seguinte erro: [DCC Error] Unit1.pas(107): E2081 Assignment to FOR-Loop variable 'i' Este erro nos informa que não é possível atribuir valor a uma variável de controle dentro do laço for. Se quisermos que o laço "conte" de trás para frente, podemos substituir a palavra-chave to por downto. Veja:
procedure TForm1.Button3Click(Sender: TObject);
var
i: Integer; // variável de controle
begin
// este laço for conta de 10 até 0
for i := 10 downto 0 do
begin
ShowMessage(IntToStr(i));
end;
end;
Para fins de compatibilidade, esta dica foi escrita usando Delphi 2009. |
C# ::: Windows Forms ::: DataGridView |
Como retornar a quantidade de linhas em um DataGridView do C# Windows FormsQuantidade de visualizações: 14911 vezes |
A quantidade de linhas em um DataGridView do C# Windows Forms pode ser obtida por meio da propriedade RowCount. Veja:
private void button2_Click(object sender, EventArgs e){
// vamos adicionar três colunas no DataGridView
dataGridView1.Columns.Add("cidade", "Cidade");
dataGridView1.Columns.Add("estado", "Estado");
dataGridView1.Columns.Add("populacao", "População");
// vamos adicionar três linhas
dataGridView1.Rows.Add("Goiânia", "GO", "3.453,39");
dataGridView1.Rows.Add("Cuiabá", "MT", "1.876,12");
dataGridView1.Rows.Add("Curitiba", "PR", "5.346,98");
// não vamos permitir que o usuário adicione novas
// linhas (o que daria uma linha a mais na nossa
// contagem
dataGridView1.AllowUserToAddRows = false;
// vamos obter a quantidade de linhas no DataGridView
int quant_linhas = dataGridView1.RowCount;
// exibe o resultado
MessageBox.Show("O DataGridView contém " +
quant_linhas + " linhas");
}
É possível também usar a propriedade RowCount para definir a quantidade de linhas em um DataGridView: dataGridView1.RowCount = 6; Há algumas considerações importantes sobre a propriedade RowCount: 1) Se seu valor for definido como 0, todas as linhas do DataGridView serão removidas; 2) Se o novo valor for menor que o valor atual, as linhas excedentes serão removidas no final da coleção Rows; 3) Se o novo valor for maior que o valor atual, as novas linhas serão adicionadas no final da coleção Rows; 4) Se tentarmos alterar o valor desta propriedade após a definição da propriedade DataSource, uma exceção InvalidOperationException será lançada. |
JavaScript ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em JavaScript usando a função cos() do objeto Math - Calculadora de cosseno em JavaScriptQuantidade de visualizações: 7627 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da linguagem JavaScript. Esta função, que é parte do objeto Math, recebe um valor numérico e retorna um valor também numérico) entre -1 até 1 (ambos inclusos). Veja:
<html>
<head>
<title>Estudos JavaScript</title>
</head>
<body>
<script type="text/javascript">
// vamos calcular o cosseno de 3 números
document.writeln("Cosseno de 0 = " + Math.cos(0));
document.writeln("<br>Cosseno de 1 = " + Math.cos(1));
document.writeln("<br>Cosseno de 2 = " + Math.cos(2));
</script>
</body>
</html>
Ao executar este código JavaScript nós teremos o seguinte resultado: Cosseno de 0 = 1 Cosseno de 1 = 0.5403023058681398 Cosseno de 2 = -0.4161468365471424 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 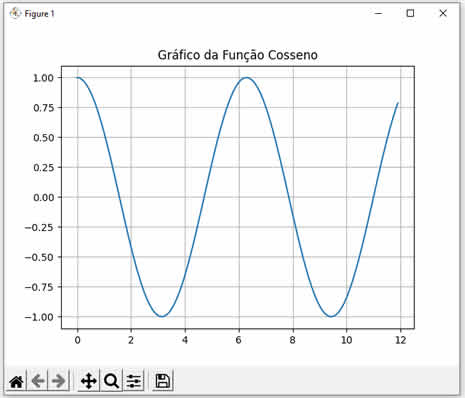 |
C# ::: Dicas & Truques ::: Gráficos |
Como desenhar gráficos em C# usando GDI+ - Computação gráfica em C# - Passos iniciasQuantidade de visualizações: 17395 vezes |
|
Qualquer um que queira iniciar os estudos e desenhos de gráficos em C# usando Windows Forms deve obrigatoriamente entender um pouco de GDI e GDI+. GDI é o acrônimo de Graphics Device Interface e GDI+ é o seu sucessor em versões mais recentes do Microsoft Windows. Com a indepedência do GDI+ podemos desenhar em um formulário, na tela ou impressora sem qualquer modificação no código. O próprio GDI+ se encarrega dos detalhes da implementação de cada um destes diferentes dispositivos. O GDI+ é uma interface de programação de aplicações (API) que forma o sub-sistema do sistema operacional Microsoft Windows XP. Esta API é a responsável pela exibição de informações na tela e impressoras. O GDI+ é uma DLL Win32 chamada de gdiplus.dll que é distribuída com o Windows XP e versões mais recentes do Windows. Esta DLL está também disponível para uso em versões do Windows anteriores ao XP. A plataforma .NET encapsula as funcionalidades do GDI+ nos seguintes namespaces: System.Drawing, System.Drawing.Drawing2D, System.Drawing.Imaging, System.Drawing.Text e System.Drawing.Printing. Antes de iniciar seus desenhos em C# e Windows Forms, é importante entender o sistema de coordenadas do GDI+. Este sistema usa a medida de pixels ("picture elements"), que é a menor unidade de resolução no display de um monitor. Assim, o canto superior esquerdo de um controle GUI (um formulário, um painel, botão, etc) tem as coordenadas (0, 0), ou seja, x = 0 e y = 0. Lembre-se de que x é o eixo horizontal e y é o eixo vertical. A classe Graphics, do pacote System.Drawing, é quem fornece boa parte dos métodos que usamos para desenhar em C# e Windows Forms. Veja sua posição na hierarquia de classes da plataforma .NET:
System.Object
System.MarshalByRefObject
System.Drawing.Graphics
Um objeto desta classe pode ser obtido com uma chamada ao método CreateGraphics() a partir de um objeto que herda de System.Windows.Forms.Control ou gerenciando o evento Paint do controle e acessando a propriedade Graphics da classe System.Windows.Forms.PaintEventArgs. Veja um trecho de código no qual desenhamos uma linha horizontal no formulário a partir do clique de um botão:
private void button1_Click(object sender, EventArgs e){
// vamos obter o Graphics do formulário
Graphics g = this.CreateGraphics();
// vamos desenhar uma linha horizontal de 300 pixels na
// cor preta e espessura de 1 pixel
g.DrawLine(new Pen(Color.Black, 1), new Point(20, 80),
new Point(320, 80));
// vamos liberar o objeto Graphics
g.Dispose();
}
|
VB.NET ::: Dicas & Truques ::: Strings e Caracteres |
Como contar as ocorrências de um caractere em uma string em VB.NET usando o método IndexOf()Quantidade de visualizações: 12846 vezes |
|
Nesta dica mostrarei como podemos usar o método IndexOf() da classe String do VB.NET e o laço While para contar quantas vezes um determinado caractere ocorre em uma palavra, frase ou string. Veja o código completo para o exemplo:
Imports System
Module Program
Sub Main(args As String())
Dim frase As String = "Gosto muito de VB.NET e você?"
Dim letra As Char = "o"
Dim quant As Integer = 0
Dim pos As Integer = -1, pos_ant As Integer = -1
Dim cont As Integer = 0
' mostra a frase
Console.WriteLine("A frase é: " & frase)
While cont < frase.Length
pos = frase.IndexOf(letra, cont)
If pos <> pos_ant And pos <> -1 Then
Console.WriteLine("""" & letra &
""" encontrada na posição " & pos)
quant += 1
End If
cont += 1
pos_ant = pos
End While
' mostra a quantidade de ocorrências da letra "o"
Console.WriteLine("Encontrei " & quant & " ocorrências da " _
& "letra " & letra)
Console.WriteLine(vbCrLf & "Pressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código VB.NET nós teremos o seguinte resultado: A frase é: Gosto muito de VB.NET e você? "o" encontrada na posição 1 "o" encontrada na posição 4 "o" encontrada na posição 10 "o" encontrada na posição 25 Encontrei 4 ocorrências da letra o |
PHP ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como adicionar novos elementos a um array PHP usando a notação [] - Adicionando elementos ao final de um array PHPQuantidade de visualizações: 15995 vezes |
|
Em várias situações nós precisamos incluir novos elementos ao final de um vetor (array) PHP. Para isso nós podemos usar a notação [], que adiciona o novo elemento ao array e incrementa sua faixa de índices automaticamente. Veja um exemplo completo no qual declaramos um vetor e em seguida usamos a notação [] para adicionar três elementos ao seu final:
<?
// vamos declarar o vetor
$pessoas = array();
// define o elemento no índice 0
$pessoas[] = "Osmar J. Silva";
// define o elemento no índice 1
$pessoas[] = "Salvador M. Andrade";
// define o elemento no índice 2
$pessoas[] = "Dyego Fernandes de Sousa";
// vamos mostrar o conteúdo do vetor
var_dump($pessoas);
?>
Ao executarmos este código nós teremos o seguinte resultado: array(3) { [0]=> string(14) "Osmar J. Silva" [1]=> string(19) "Salvador M. Andrade" [2]=> string(24) "Dyego Fernandes de Sousa" } Esta dica foi revisada e testado no PHP 8. |
Java ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como testar se uma matriz é uma matriz identidade usando JavaQuantidade de visualizações: 1163 vezes |
|
Seja M uma matriz quadrada de ordem n. A matriz M é chamada de Matriz Identidade de ordem n (indicada por In) quando os elementos da diagonal principal são todos iguais a 1 e os elementos restantes são iguais a zero. Para melhor entendimento, veja a imagem de uma matriz identidade de ordem 3, ou seja, três linhas e três colunas: 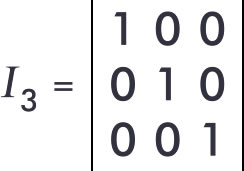 Veja um código Java completo no qual nós declaramos uma matriz quadrada de ordem 3, pedimos para o usuário informar os valores de seus elementos e no final informamos se a matriz é uma matriz identidade ou não:
package estudos;
import java.util.Scanner;
public class Estudos{
public static void main(String[] args){
int n = 3; // ordem da matriz quadrada
int matriz[][] = new int[n][n]; // matriz quadrada
// para efetuar a leitura do usuário
Scanner entrada = new Scanner(System.in);
// vamos pedir para o usuário informar os elementos da matriz
for (int i = 0; i < n; i++){
for (int j = 0; j < n; j++) {
System.out.print("Elemento na linha " + (i + 1) +
" e coluna " + (j + 1) + ": ");
matriz[i][j] = Integer.parseInt(entrada.nextLine());
}
}
// agora verificamos se a matriz é uma matriz identidade
boolean identidade = true;
for(int linha = 0; linha < n; linha++){
for(int coluna = 0; coluna < n; coluna++){
if(matriz[linha][coluna] != 1 && matriz[coluna][linha] != 0){
identidade = false;
break;
}
}
}
// agora mostramos a matriz lida
System.out.printf("\n");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.printf("%d ", matriz[i][j]);
}
System.out.printf("\n");
}
if (identidade){
System.out.printf("\nA matriz informada é uma matriz identidade.\n");
}
else{
System.out.printf("\nA matriz informada não é uma matriz identidade.\n");
}
}
}
Ao executar este código Java nós teremos o seguinte resultado: Elemento na linha 1 e coluna 1: 1 Elemento na linha 1 e coluna 2: 0 Elemento na linha 1 e coluna 3: 0 Elemento na linha 2 e coluna 1: 0 Elemento na linha 2 e coluna 2: 1 Elemento na linha 2 e coluna 3: 0 Elemento na linha 3 e coluna 1: 0 Elemento na linha 3 e coluna 2: 0 Elemento na linha 3 e coluna 3: 1 1 0 0 0 1 0 0 0 1 A matriz informada é uma matriz identidade. |
Python ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a equação reduzida da reta em Python dados dois pontos pertencentes à retaQuantidade de visualizações: 3376 vezes |
|
Nesta dica de Python veremos como calcular a equação reduzida da reta quando temos dois pontos pertencentes à esta reta. Não, nessa dica não vamos calcular a equação geral da reta, apenas a equação reduzida. Em outras dicas do site você encontra como como isso pode ser feito. Para relembrar: a equação reduzida da reta é y = mx + n, em que x e y são, respectivamente, a variável independente e a variável dependente; m é o coeficiente angular, e n é o coeficiente linear. Além disso, m e n são números reais. Com a equação reduzida da reta, é possível calcular quais são os pontos que pertencem a essa reta e quais não pertencem. Vamos começar então analisando a seguinte figura, na qual temos dois pontos que pertencem à uma reta: 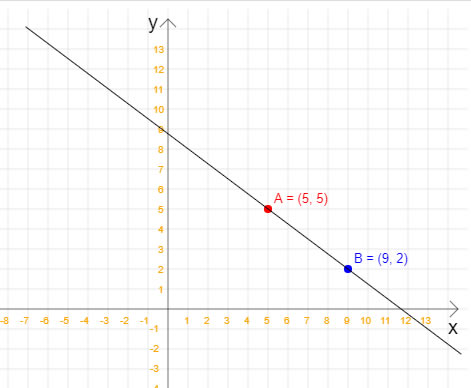 Note que a reta da figura passa pelos pontos A(5, 5) e B(9, 2). Então, uma vez que já temos os dois pontos, já podemos calcular a equação reduzida da reta. Veja o código Python completo para esta tarefa:
# método principal
def main():
# vamos ler as coordenadas do primeiro ponto
x1 = float(input("Coordenada x do primeiro ponto: "))
y1 = float(input("Coordenada y do primeiro ponto: "))
# vamos ler as coordenadas do segundo ponto
x2 = float(input("Coordenada x do segundo ponto: "))
y2 = float(input("Coordenada y do segundo ponto: "))
sinal = "+"
# vamos calcular o coeficiente angular da reta
m = (y2 - y1) / (x2 - x1)
# vamos calcular o coeficiente linear
n = y1 - (m * x1)
# coeficiente linear menor que zero? O sinal será negativo
if (n < 0):
sinal = "-"
n = n * -1
# mostra a equação reduzida da reta
print("Equação reduzida: y = %.2fx %s %.2f" % (m, sinal, n))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 5 Coordenada y do primeiro ponto: 5 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 2 Equação reduzida: y = -0,75x + 8,75 Para testarmos se nossa equação reduzida da reta está realmente correta, considere o valor 3 para o eixo x da imagem acima. Ao efetuarmos o cálculo: >> y = (-0.75 * 3) + 8.75 y = 6.5000 temos o valor 6.5 para o eixo y, o que faz com que o novo ponto caia exatamente em cima da reta considerada na imagem. |
Nossas 20 dicas & truques de programação mais populares |
|
Delphi - Como habilitar ou desabilitar um TEdit do Delphi usando a função EnableWindow() da API do Windows |
Você também poderá gostar das dicas e truques de programação abaixo |
|
JavaScript - Cookies em JavaScript - Como registrar a quantidade de vezes que o usuário visitou a sua página HTML AutoLISP - Como desenhar uma linha no AutoCAD usando AutoLISP - Dois pontos geométricos e o comando LINE |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




