Java ::: Fundamentos da Linguagem ::: Variáveis e Constantes

Curso Completo de Java - Como usar constantes em Java

Quantidade de visualizações: 15545 vezes
O valor de uma variável pode ser alterado durante a execução do programa. Mas, o valor de uma constante não é alterado jamais. Escritas sempre com letras maiúsculas, as constantes trazem algumas vantagens, entre elas o fato de que nomes descritivos para constantes podem tornar o programa mais fácil de ser lido. Além disso, o valor representado pela constante pode ser alterado em apenas um lugar do código fonte.

Veja abaixo como declarar e usar uma constante em Java:

// Este exemplo mostra como declarar e usar
// uma constante em Java

public class Estudos{
  final static int IDENT_PROGRAMA = 47; 
  
  public static void main(String args[]){
    System.out.println("O valor da constante " +
      "é " + IDENT_PROGRAMA);
    System.exit(0);
  }
}

Observe que usamos o modificador final para marcar um identificador como constante. Veja agora o que acontece quando tentamos alterar o valor de uma constante em tempo de compilação:

// vamos tentar alterar o valor da constante
IDENT_PROGRAMA = 29;

O compilador emitirá a seguinte mensagem de erro:

Estudos.java:9: cannot assign a value to final 
variable IDENT_PROGRAMA
  IDENT_PROGRAMA = 29;
  ^
1 error


Java ::: Desafios e Lista de Exercícios Resolvidos ::: Programação Orientada a Objetos

Algorítmos Resolvidos de Java - A classe Retangulo (construtores, getters e setters, encapsulamento e static)

Quantidade de visualizações: 15485 vezes
Exercícios Resolvidos de Java - A classe Retangulo (construtores, getters e setters, encapsulamento e static)

Pergunta/Tarefa:

Escreva uma classe Retangulo para representar um retângulo. A classe deve conter:

a) Dois campos de dados do tipo double chamados largura e altura que especificam a largura e a altura do retângulo. Os valores padrões são 1 tanto para a largura quanto para a altura.

b) Um campo de dado do tipo String chamado cor que especifica a cor do retângulo. Para este exercício em particular, assuma que TODOS os retângulos possuirão a mesma cor. A cor padrão é branco.

c) Um construtor sem argumentos que cria um retângulo padrão.

d) Um construtor que cria um retângulo com a largura e altura especificadas.

e) Métodos get() e set() para os três campos de dados da classe.

f) Um método chamado getArea() que retorna a área do retângulo.

g) Um método chamado getPerimetro() que retorna o perímetro do retângulo.

Escreva um programa de teste que cria dois objetos da classe Retangulo. Sua saída deverá ser parecida com:



Resposta/Solução:

Veja a resolução comentada deste exercício usando Java console:

Retangulo.java

package estudos;

public class Retangulo {
  private double largura; // largura do retângulo
  private double altura; // altura do retângulo
  
  // O exercício pede que TODOS os retângulos tenham a mesma cor
  // consulte a dica http://www.arquivodecodigos.net/dicas/1158 para mais
  // detalhes sobre o modificador static
  private static String cor = "branco"; // cor do retângulo

  // construtor sem argumentos
  public Retangulo(){
    this.largura = 1;
    this.altura = 1;
  }

  // construtor que permite especificar a largura e a altura
  public Retangulo(double largura, double altura){
    this.largura = largura;
    this.altura = altura;
  }

  // obtém a altura
  public double getAltura() {
    return altura;
  }

  // define a altura
  public void setAltura(double altura){
    this.altura = altura;
  }

  // obtém a largura
  public double getLargura(){
    return largura;
  }

  // define a largura
  public void setLargura(double largura){
    this.largura = largura;
  }
  
  // obtém a cor de TODOS os retângulos
  public static String getCor(){
    return cor;
  }

  // define a cor de TODOS os retângulos
  public static void setCor(String cor){
    Retangulo.cor = cor;
  }

  // este método retorna a área do retângulo (em metros quadrados)
  public double getArea(){
    return (this.largura * this.altura);  
  }
  
  // este método retorna o perímetro do retângulo (em metros)
  public double getPerimetro(){
    return ((2 * this.largura) + (2 * this.altura));  
  }
}

Agora o teste no método main():

package estudos;

public class Estudos {
  public static void main(String[] args) {
    // vamos criar uma instância da classe Retangulo com
    // os valores padrões
    Retangulo a = new Retangulo();
    
    // agora vamos informar a largura e a altura
    Retangulo b = new Retangulo(10, 5);
    
    // os dois retângulos terão a cor verde
    Retangulo.setCor("verde");
    
    // vamos mostrar os resultados do primeiro retângulo
    System.out.println("Primeiro retângulo");
    System.out.println("Largura: " + a.getLargura());
    System.out.println("Altura: " + a.getAltura());
    System.out.println("Cor: " + Retangulo.getCor());
    System.out.println("Área: " + a.getArea() + " metros quadrados");
    System.out.println("Perímetro: " + a.getPerimetro() + " metros");
    
    // vamos mostrar os resultados do segundo retângulo
    System.out.println("\nSegundo retângulo");
    System.out.println("Largura: " + b.getLargura());
    System.out.println("Altura: " + b.getAltura());
    System.out.println("Cor: " + Retangulo.getCor());
    System.out.println("Área: " + b.getArea() + " metros quadrados");
    System.out.println("Perímetro: " + b.getPerimetro() + " metros");
  }
}


JavaScript ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas

Como calcular a área de um círculo em JavaScript dado o raio do círculo

Quantidade de visualizações: 7470 vezes
A área de um círculo pode ser calculada por meio do produto entre a constante PI e a medida do raio ao quadrado (r2). Comece analisando a figura abaixo: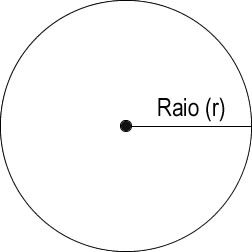



Sendo assim, temos a seguinte fórmula:



Onde A é a área, PI equivale a 3,14 (aproximadamente) e r é o raio do círculo.

A área do círculo é igual a calcular a área da circunferência. Lembrando que a medida da área do círculo e da circunferência é uma medida aproximada.

O raio é a medida que vai do centro até um ponto da extremidade do círculo. O diâmetro é a medida equivalente ao dobro da medida do raio, passando pelo centro do círculo e dividindo-o em duas partes. A medida do diâmetro é 2 * PI.

Veja agora um código JavaScript completo (incluindo a página HTML) que calcula a área de um círculo mediante a informação do raio:

<!doctype html>
<html>
<head>
 <title>Estudos JavaScript</title>
</head>
<body>

<script type="text/javascript">
  // efetua a leitura do raio
  var raio = parseFloat(window.prompt("Informe o raio do círculo:"));
  // calcula a área
  var area = Math.PI * Math.pow(raio, 2);
  // mostra o resultado
  document.writeln("A area do círculo de raio " +
    raio + " é igual a " + area);
</script>

</body>
</html>

Ao executarmos este código nós teremos o seguinte resultado:

Informe o raio do círculo: 5
A area do círculo de raio 5 é igual a 78.53981633974483

Java ::: Java para Engenharia ::: Unidades de Medida

Como converter Quilograma-Força para Newton em Java - Java para Física

Quantidade de visualizações: 451 vezes
Nesta dica mostrarei como podemos efetuar a conversão de Quilograma-Força para Newton usando Java. Este cálculo é comum quando estamos tentando resolver problemas de Física usando programação.

Antes de continuarmos, vamos revisar estas duas unidades de medida. O Quilograma-Força (kgf) é a unidade de medida de uma força que faz um objeto com uma massa de 1 kg acelerar em um metro por segundo ao quadrado (1 m/s2). O Newton é a unidade utilizada para medir força no Sistema Internacional de Unidades (SI).

Agora vamos à fórmula para transformar Quilograma-Força em Newton. Veja:

\[\text{Newton} = \text{Quilograma-Força} \cdot 9,8 \]

Note que só precisamos multiplicar Quilograma-Força por 9,8 para obtermos o resultado em Newton.

Vamos ver um exemplo? Veja um código Java completo que pede para o usuário informar um valor em Quilograma-Força e o converte para Newton:

package estudos;

import java.util.Scanner;

public class Estudos {
  public static void main(String[] args) {
    // variáveis usadas na resolução do problema
    double kgf, newton; 

    // para ler a entrada do usuário
    Scanner entrada = new Scanner(System.in);
    
    // vamos ler o valor em Quilograma-Força
    System.out.print("Informe o valor em kgf: ");
    kgf = Double.parseDouble(entrada.nextLine());
    
    // agora vamos fazer a conversão para Newton
    newton = kgf * 9.80665;
    
    // e mostramos o resultado
    System.out.println("O resultado é: " + newton + " N");
  }
}

Ao executarmos este código Java nós teremos o seguinte resultado:

Informe o valor em kgf: 50
O resultado é: 490.3325 N

Java ::: Coleções (Collections) ::: HashMap

Como adicionar novos mapeamentos chave-valor a um HashMap do Java usando o método put()

Quantidade de visualizações: 9609 vezes
Novos mapeamentos chave-valor são adicionados a um HashMap da linguagem Java usando-se o método put(). Veja sua assinatura:

public V put(K key, V value)


Note que este método recebe a chave e o valor a ser inserido e retorna um objeto do mesmo tipo daquele fornecido no segundo argumento. Este retorno é muito útil para sabermos se o novo valor não sobrepôs um valor já existente. Se o retorno for null, o novo valor foi inserido. Caso contrário o retorno será o valor existente antes da sobreposição. Apenas tenha cuidado com valores null existentes como chaves ou valores. Nestes casos o retorno do método put não ajudará em nada.

Veja um exemplo do uso do método put():

package estudos;

import java.util.*;

public class Estudos{
  public static void main(String[] args){
    
    // vamos criar uma instância de HashMap
    HashMap<Integer, String> clientes = new HashMap<Integer, String>();

    // vamos adicionar três chaves e seus valores
    clientes.put(new Integer(1), "Osmar J. Silva");
    clientes.put(new Integer(2), "Salvador Miranda de Andrade");
    clientes.put(new Integer(3), "Marcos da Costa Santos");

    // é possível também referenciar o valor adicionado
    // ao HashMap, uma vez que este é o retorno do métoto put()
    String nome = clientes.put(new Integer(2), "Carlos"); 

    if(nome == null){
      System.out.println("Novo valor inserido com sucesso");
    }
    else{
      System.out.println("Valor já existia. Houve sopreposição"); 
    }

    System.exit(0);
  }
}

Ao executar este código Java nós teremos o seguinte resultado:

Valor já existia. Houve sopreposição

Java ::: Pacote java.awt ::: Graphics

Como retornar a cor atual do contexto de desenho usando o método getColor() da classe Graphics do Java - Computação gráfica em Java

Quantidade de visualizações: 7952 vezes
Antes de efetuar qualquer desenho na superfície de um componente, é importante saber qual cor está definida no momento, assim podemos alterá-la se necessário. Para isso podemos usar o método getColor() da classe Graphics. Este método retorna um objeto da classe Color.

Veja um exemplo no qual obtemos a cor usada atualmente para desenhar na superfície de um JLabel:

import java.awt.*;
import java.awt.event.*;
import javax.swing.*;

public class Estudos extends JFrame{
  JLabel label;  

  public Estudos() {
    super("Desenhando");
    
    Container c = getContentPane();
    c.setLayout(new BorderLayout());

    // Cria um JLabel
    label = new JLabel();
    c.add(label, BorderLayout.CENTER);

    // Cria um botão
    JButton btn = new 
      JButton("Obter a cor do contexto");
    btn.addActionListener(
      new ActionListener(){
        public void actionPerformed(ActionEvent e){
          
          Graphics graphics = label.getGraphics();
          
          // obtém a cor usada para desenhar no
          // contexto de desenho
          Color cor = graphics.getColor();
          JOptionPane.showMessageDialog(null,
            "A cor usada atualmente é " +
            cor.toString());
        }
      }
    );
    
    // Adiciona o botão à janela
    c.add(btn, BorderLayout.SOUTH);

    setSize(350, 250);
    setVisible(true);
  }
  
  public static void main(String args[]){
    Estudos app = new Estudos();
    app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
  }
}

Ao executar este código Java nós teremos o seguinte resultado:

A cor usada atualmente é java.awt.Color[r=0,g=0,b=0]

GNU Octave ::: Desafios e Lista de Exercícios Resolvidos ::: Pesquisa Operacional

Exercício Resolvido de Octave - Programação Linear - Um fazendeiro decidiu misturar duas rações, a Ração X e a Ração Y. Cada porção de ração dada aos animais

Quantidade de visualizações: 399 vezes
Pergunta/Tarefa:

Este exercício de Octave aborda o uso da função glpk() para resolver um problema de Pesquisa Operacional usando Programação Linear.

1) Um fazendeiro decidiu misturar duas rações, a Ração X e a Ração Y. Cada porção de ração dada aos animais exige 60g de proteína e 30g de gordura. A Ração X possui 15g de proteína e 10g de gordura, e custa R$ 80,00 a unidade. A Ração Y apresenta 20g de proteína e 5g de gordura e custa R$ 50,00 a unidade.

Quanto de cada ração deve ser usada para minimizar os custos do fazendeiro?

Sua saída deverá ser parecida com:

A solução para o problema de minimização é:

x = 2.40
y = 1.20

O custo mínimo é: 252.00
Resposta/Solução:

Antes de passarmos ao código Octave, vamos fazer a modelagem matemática do problema. O primeiro passo é identificar as variáveis. Assim, vamos chamar de x o número de unidades da Ração X e de y o número de unidades da Ração Y. Veja:

x = Número de unidades da Ração X
y = Número de unidades da Ração Y

E então temos a função custo:

custo = 80x + 50y

A primeira restrição diz respeito à quantidade de proteína em cada porção de ração. Sabendo que a Ração X apresenta 15g de proteína e a Ração Y apresenta 20g de proteína nós temos:

R1: 15x + 20y >= 60 (proteína)

A segunda restrição diz respeito à quantidade de gordura em cada porção de ração. Sabendo que a Ração X apresenta 10g de gordura e a Ração Y apresenta 5g de gordura nós temos:

R2: 10x + 5y >= 30 (gordura)

As restrições R3 e R4 dizem respeito à não negatividade das variáveis de decisão:

R3: x >= 0
R4: y >= 0

Veja agora o código Octave completo (pesquisa_operacional.m): 

# vamos começar definindo a matriz que representa a função de
# minimização
c = [80.0, 50.0]';

# agora a matriz de restrições
A = [15, 20; 10, 5];
b = [60, 30]';

# as restrições de não negatividade e o limite superior
lb = [0, 0]';
ub = [];

# definimos as restrições como limites inferiores
ctype = "LL";

# indicamos que vamos usar variáveis contínuas (não inteiros)
vartype = "CC";

# vamos usar minimização, por isso definimos o valor 1. Se fosse
# maximização o valor seria -1
s = 1;

# definimos os parâmetros adicionais
param.msglev = 1;
param.itlim = 100;

# e chamamos a função glpk()
[xmin, fmin, status, extra] = glpk(c, A, b, lb, ub, ctype, vartype, s, param);

# mostramos a solução para o problema de minimização
printf("A solução para o problema de minimização é:\n\n");
printf("x = %.2f\n", xmin(1));
printf("y = %.2f\n", xmin(2));

# para finalizar vamos mostrar o custo mínimo
printf("\nO custo mínimo é: %.2f\n\n", fmin);

Ao executar o código você perceberá que, para minimizar os custos do fazendeiro, deverão ser usados na mistura 2,4 unidades da Ração X e 1,2 unidades da Raça Y, a um custo mínimo de R$ 252,00.

Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear

Como converter Coordenadas Cartesianas para Coordenadas Polares usando Python

Quantidade de visualizações: 5758 vezes
Nesta nossa série de Python para Geometria Analítica e Álgebra Linear, mostrarei um código 100% funcional para fazer a conversão entre coordenadas cartesianas e coordenadas polares. Esta operação é muito frequente em computação gráfica e é parte integrante das disciplinas dos cursos de Engenharia (com maior ênfase na Engenharia Civil).

Na matemática, principalmente em Geometria e Trigonometria, o sistema de Coordenadas no Plano Cartesiano, ou Espaço Cartesiano, é um sistema que define cada ponto em um plano associando-o, unicamente, a um conjuntos de pontos numéricos.

Dessa forma, no plano cartesiano, um ponto é representado pelas coordenadas (x, y), com o x indicando o eixo horizontal (eixo das abscissas) e o y indicando o eixo vertical (eixo das ordenadas). Quando saímos do plano (espaço 2D ou R2) para o espaço (espaço 3D ou R3), temos a inclusão do eixo z (que indica profundidade).

Já o sistema de Coordenadas Polares é um sistema de coordenadas em duas dimensões no qual cada ponto no plano é determinado por sua distância a partir de um ponto de referência conhecido como raio (r) e um ângulo a partir de uma direção de referência. Este ângulo é normalmente chamado de theta (__$\theta__$). Assim, um ponto em Coordenadas Polares é conhecido por sua posição (r, __$\theta__$).

Antes de prosseguirmos, veja uma imagem demonstrando os dois sistemas de coordenadas: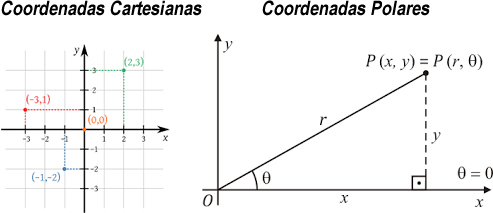



A fórmula para conversão de Coordenadas Cartesianas para Coordenadas Polares é:

__$r = \sqrt{x^2+y2}__$
__$\theta = \\arctan\left(\frac{y}{x}\right)__$

E aqui está o código Python completo que recebe as coordenadas cartesianas (x, y) e retorna as coordenadas polares (r, __$\theta__$):

# importamos a bibliteca NumPy
import numpy as np
import math as math
  
def main():
  # vamos ler as coordenadas cartesianas
  x = float(input("Valor de x: "))
  y = float(input("Valor de y: "))

  # vamos calcular o raio
  raio = math.sqrt(math.pow(x, 2) + math.pow(y, 2))  

  # agora calculamos o theta (ângulo) em radianos 
  theta = np.arctan2(y, x)

  # queremos o ângulo em graus também
  angulo_graus = 180 * (theta / math.pi) 

  # e exibimos o resultado
  print("As Coordenadas Polares são:")
  print("raio = %0.4f, theta = %0.4f, ângulo em graus = %0.2f" 
    % (raio, theta, angulo_graus))

if __name__== "__main__":
  main()

Ao executar este código nós teremos o seguinte resultado:

Valor de x: -1
Valor de y: 1
As Coordenadas Polares são:
raio = 1.4142, theta = 2.3562, ângulo em graus = 135.00

Veja que as coordenadas polares equivalentes são (__$\sqrt{2}__$, __$\frac{3\pi}{4}__$), com o theta em radianos. Sim, os professores das disciplinas de Geometria Analítica e Álgebra Linear, Física e outras gostam de escrever os resultados usando raízes e frações em vez de valores reais.

C# ::: Dicas & Truques ::: Data e Hora

Como testar se um ano é bissexto em C# usando a função IsLeapYear() da classe DateTime

Quantidade de visualizações: 14438 vezes
Podemos verificar se um determinando ano é bissexto usando o método IsLeapYear() da estrutura DateTime. Este método recebe um valor inteiro representando o ano com 4 dígitos e retorna um valor true ou false. Veja o exemplo:

static void Main(string[] args){
  // vamos verificar se o ano 2008
  // é bissexto
  int ano = 2008;

  if(DateTime.IsLeapYear(ano)){
    Console.WriteLine("O ano informado é bissexto");
  }
  else{
    Console.WriteLine("O ano informado NÃO é bissexto");
  }

  // pausa o programa
  Console.ReadKey();
}

Este método pode disparar uma exceção ArgumentOutOfRangeException se o valor do ano for menor que 1 ou maior que 9999.

C# ::: Dicas & Truques ::: Arquivos e Diretórios

Como adicionar conteúdo ao final de um arquivo em C# usando as classes FileStream e StreamWriter

Quantidade de visualizações: 10279 vezes
Nesta dica mostro como usar as classes FileStream e StreamWriter para adicionar conteúdo a um arquivo já existente. Note que usamos o construtor de FileStream que aceita o caminho e nome do arquivo e o modo que ele será aberto. Ao fornecer o valor FileMode.Append nós estamos informando que, se o arquivo existir, mais conteúdo será adicionando ao seu final. Do contrário o arquivo é criado.

Já no construtor de StreamWriter nós estamos fornecendo a codificação dos caracteres, neste caso, UTF-8. Para finalizar, escrevemos no arquivo usando os métodos Write() e WriteLine() da classe StreamWriter.

Veja o código:

static void Main(string[] args){
  // vamos criar uma instância de FileStream. Note que neste
  // construtor nós estamos informando o caminho e nome do
  // arquivo e o modo de abertura do arquivo. Se o arquivo já existir
  // o novo conteúdo é adicionado. Se não existir, o arquivo é criado
  FileStream fs = new FileStream("dados.txt", FileMode.Append);

  // já temos o FileStream? vamos fornecê-lo a um StreamWriter
  StreamWriter sw = new StreamWriter(fs, Encoding.UTF8);

  // vamos escrever ou adicioar conteúdo no arquivo
  sw.WriteLine("Esta é mais uma linha");
  sw.Write("Hoje é: ");
  sw.WriteLine(DateTime.Now);
  sw.WriteLine("Esta é a última linha");
  
  sw.Flush();
  sw.Close();
  fs.Close();

  Console.WriteLine("Acabei de escrever no arquivo");
  Console.WriteLine("Pressione qualquer tecla para sair...");
  // pausa o programa
  Console.ReadKey();
}

Ao executar este código C# nós teremos o seguinte resultado:

Acabei de escrever no arquivo
Pressione qualquer tecla para sair...

Carregar Publicações Anteriores

Nossas 20 dicas & truques de programação mais populares

Você também poderá gostar das dicas e truques de programação abaixo

Nossas 20 dicas & truques de programação mais recentes

Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site

Últimos Exercícios Resolvidos

E-Books em PDF
E-Book 350 Exercícios Resolvidos de Java - PDF com 500 páginas
Domine lógica de programação e a linguagem Java com o nosso E-Book 350 Exercícios Exercícios de Java, para você estudar onde e quando quiser.

Este e-book contém exercícios resolvidos abrangendo os tópicos: Java básico, matemática e estatística, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.
Ver Conteúdo do E-book
E-Book 650 Dicas, Truques e Exercícios Resolvidos de Python - PDF com 1.200 páginas
Domine lógica de programação e a linguagem Python com o nosso E-Book 650 Dicas, Truques e Exercícios Exercícios de Python, para você estudar onde e quando quiser.

Este e-book contém dicas, truques e exercícios resolvidos abrangendo os tópicos: Python básico, matemática e estatística, banco de dados, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.
Ver Conteúdo do E-book

Linguagens Mais Populares

1º lugar: Java
2º lugar: Python
3º lugar: C#
4º lugar: PHP
5º lugar: C
6º lugar: Delphi
7º lugar: JavaScript
8º lugar: C++
9º lugar: VB.NET
10º lugar: Ruby
Questões de Concurso para Engenharia Civil
Fundações
Instalações Hidráulicas Prediais
Fenômenos de Transporte e Hidráulica
Estruturas de Aço e Madeira
Exercícios Resolvidos
Lista de Exercícios Resolvidos de Java
Lista de Exercícios Resolvidos de C
Lista de Exercícios Resolvidos de C++
Bancos de Dados
MySQL
Firebird
MS SQL Server
PostgreSQL
Questões de Concurso
Topografia
Hidrologia
Hidrostática
Ética e Legislação Profissional
Frameworks
jQuery
AngularJS
React / ReactJS / React.js
Laravel
Projetos e Códigos Fonte
Projetos e Códigos Fonte Java
Projetos e Códigos Fonte PHP
Projetos e Códigos Fonte Python
Especializações
Data Science
Calculadoras
Calculadoras de Topografia
Calculadoras de Matemática
Calculadoras de Data e Hora
Calculadoras de Física
Calculadoras de Estatística
Calculadoras de Trigonometria
Calculadoras de Matrizes
Calculadoras de Vetores
Ferramentas
Tabela de Cores Flat Design
Tabela de Cores do Material Design do Google
Tabela de Cores Web Safe Colors
Todas as Linguagens, Frameworks, Biliotecas e Bancos de Dados
.NET Framework | ActionScript | Adobe AIR | Adobe Flex | AJAX | Android Java | Angular | AngularJS | Apache Ant | Apache Maven | Apache Tomcat | Apache Web Server | Arduino | ASP.NET | AutoCAD | AutoCAD .NET API C# | AutoCAD Civil 3D | AutoCAD Civil 3D .NET C# | AutoCAD VBA | AutoLISP | Bourne Again Shell (bash Shell) | C | C# | C++ | C++ Builder | CodeIgniter | CSS | Dart | Data Science | Delphi | DHTML (Dynamic HTML) | Django | Eclipse IDE | Elixir | Enterprise JavaBeans (EJB) | Erlang | Excel | Excel VBA | Ext JS | Facelets | Firebird | Flutter | Fórmulas da Física | Geral | GNU Octave | GoLang | Groovy | GTK+ | Haskell | HEC-RAS | Hibernate | HTML/XHTML | HTML5 | IBM DB2 | iReport | iTextSharp | Java | Java Servlets | JavaFX | JavaScript | JBoss | JPA - Java Persistence Architecture API - Arquitetura de Persistência Java | jQuery | jQuery UI | JSF - Java Server Faces | JSP (Java Server Pages) | Kotlin | Laravel | Linux | LISP | MongoDB | MS SQL Server | MySQL | NetBeans IDE | NetBeans IDE | Node.js | Perl | PHP | PHP-GTK | Portugol | PostgreSQL | Processing.py | Python | QGIS | Qt | R | React | React Native | React.js | Revit C# | Revit Python Shell | Ruby | Ruby On Rails | Rust | Smarty | Struts | Struts 2 | Tcl e Tcl/Tk | TypeScript | VB.NET | VBA | Visual LISP | VisuAlg | WebGL (Web Graphics Library) | wxWidgets | Zend Framework |

© 2025 Arquivo de Códigos - Todos os direitos reservados
Neste momento há 24 usuários muito felizes estudando em nosso site.