C# ::: Dicas & Truques ::: Arquivos e Diretórios |
Como renomear um diretório em C# usando o método MoveTo() da classe DirectoryInfoQuantidade de visualizações: 9699 vezes |
|
Nesta dica mostrarei como podemos usar a função MoveTo() da classe DirectoryInfo para renomear um diretório na linguagem C#. Note que, na verdade, o que o método MoveTo() faz é mover todo o conteúdo de um diretório (incluindo seu conteúdo) para um novo diretório, o que dá o mesmo resultado que simplesmente renomear o diretório antigo. Veja um exemplo completo de seu uso:
using System;
using System.IO;
namespace Estudos {
class Program {
static void Main(string[] args) {
// vamos criar uma instância da classe DirectoryInfo
DirectoryInfo dir = new DirectoryInfo(@"C:\estudos_csharp\teste");
try {
// vamos chamar o método MoveTo() para renomear o diretório
dir.MoveTo(@"C:\estudos_csharp\teste_2");
Console.WriteLine("Diretório renomeado com sucesso.");
}
catch (Exception e) {
Console.WriteLine("Não foi possível renomear o diretório: {0}", e.ToString());
}
finally { }
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Diretório renomeado com sucesso. |
Delphi ::: Dicas & Truques ::: Strings e Caracteres |
Como converter todo o conteúdo de uma string para letras maiúsculas em Delphi usando a função AnsiUpperCase()Quantidade de visualizações: 17242 vezes |
Algumas vezes precisamos converter todo o conteúdo de uma string para letras maiúsculas. Em Delphi isso pode ser feito com o auxílio da função AnsiUpperCase(). Esta função recebe uma string e retorna outra string com todos os caracteres maiúsculos. Veja o exemplo:procedure TForm1.Button1Click(Sender: TObject); var nome: string; begin nome := 'Osmar'; // vamos converter a string para letras maiúsculas nome := AnsiUpperCase(nome); // exibe o resultado ShowMessage(nome); end; Note que esta função suporta caracteres de mais de um byte e com acentuações. Para questões de compatibilidade, esta dica foi escrita usando Delphi 2009. |
React Native ::: React Native - Componentes Visuais ::: Button |
Como detectar um clique em um botão do React Native e exibir uma mensagem AlertQuantidade de visualizações: 1348 vezes |
|
Nesta dica mostrarei como detectar um evento onPress em um botão do React Native e exibir uma mensagem usando o método alert() do componente Alert. Note que o evento onPress é disparado quando o usuário pressiona o botão. Veja o código completo para o exemplo:
import React, {Component} from 'react';
import {View, Button, Alert} from 'react-native';
type Props = {};
export default class App extends Component<Props> {
render() {
return (
<View style={{backgroundColor: '#eeeeee',
padding: 30}}>
<Button onPress = {() =>
Alert.alert("Bem-vindo(a) ao React Native")}
title="Clique" />
</View>
);
}
}
Veja que este exemplo define o código a ser chamado quando o botão for clicado diretamente em sua declaração. Em outras dicas dessa seção você verá como clicar no botão e chamar uma função JavaScript residente fora da declaração do botão. |
Java ::: Fundamentos da Linguagem ::: Tipos de Dados |
Apostila Java para iniciantes - Como usar o tipo de dados referência em seus códigos JavaQuantidade de visualizações: 11566 vezes |
O Java contém 8 tipos de dados primitivos e um tipo referência. No entanto, poucos livros dedicam exemplos a este último tipo. Vamos começar analisando o trecho de código abaixo:
public class Estudos{
public static void main(String args[]){
String nome = "Osmar J. Silva";
System.out.println(nome);
System.exit(0);
}
}
Se observarmos este código, veremos que a variável nome não é um tipo primitivo e sim uma referência. Desta forma, qualquer variável ou constante que não seja do tipo primitivo é uma referência a um objeto de uma classe, interface, etc. Arrays não são tipos primitivos também. Assim, variáveis ou constantes que apontam para arrays (vetores e matrizes) também são referências. É importante entender bem a noção de referências, visto que é por meio delas que acessamos um determinado objeto na memória. Além disso, como objetos e arrays são sempre passados por referência aos métodos Java, fica fácil entender como várias referências podem apontar para o mesmo objeto ao mesmo tempo. E, caso você tenha esquecido, os tipos primitivos nunca são passados por referêcia aos métodos. Em vez disso, eles são passados por valor (o que quer dizer que uma alteração nos argumentos fornecidos ao métodos não altera a cópia original da variável). |
Java ::: Classes e Componentes ::: JTable |
Java Swing - Como obter a quantidade de colunas em uma JTable usando o método getColumnCount()Quantidade de visualizações: 64 vezes |
|
Nesta dica mostrarei como é possível contar as colunas de uma JTable com uma chamada ao método getColumnCount() da interface TableModel, que representa os dados contidos na tabela. Note que, neste exemplo, eu escrevi toda a aplicação Java Swing "na unha", ou seja, sem nenhum editor visual. Esta técnica é boa para entender todas as partes que compoem uma aplicação Java Swing. Veja o código completo:
package arquivodecodigos;
import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
public class Estudos extends JFrame{
public Estudos(){
super("Exemplo de uma tabela simples");
// colunas da tabela
String[] colunas = {"Cidade", "Estado", "Habitantes"};
// conteúdo da tabela
Object[][] conteudo = {
{"Goiânia", "GO", "43.023.432"},
{"São Paulo", "SP", "5.343.234"},
{"Rio de Janeiro", "RJ", "6.434.212"},
{"Jussara", "GO", "87.454"},
{"Barra do Garças", "MT", "64.344"}
};
// constrói a tabela
final JTable tabela = new JTable(conteudo, colunas);
tabela.setPreferredScrollableViewportSize(
new Dimension(350, 50));
Container c = getContentPane();
c.setLayout(new FlowLayout());
JButton btn = new JButton("Número de Colunas");
btn.addActionListener(
new ActionListener(){
public void actionPerformed(ActionEvent e){
JOptionPane.showMessageDialog(null,
"Quantidade de colunas: " +
tabela.getModel().getColumnCount(),
"JTable", JOptionPane.INFORMATION_MESSAGE);
}
}
);
JScrollPane scrollPane = new JScrollPane(tabela);
c.add(scrollPane);
c.add(btn);
setSize(400, 300);
setVisible(true);
}
public static void main(String args[]){
Estudos app = new Estudos();
app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
}
Ao executar este exemplo e clicar no botão nós veremos uma mensagem JOptionPane.showMessageDialog() com o seguinte texto: Quantidade de colunas: 3 |
Delphi ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em Delphi dados dois pontos no plano cartesianoQuantidade de visualizações: 1375 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem Delphi que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
procedure TForm4.Button2Click(Sender: TObject);
var
x1, y1, x2, y2, m: Double;
begin
// x e y do primeiro ponto
x1 := 3;
y1 := 6;
// x e y do segundo ponto
x2 := 9;
y2 := 10;
// agora vamos calcular o coeficiente angular
m := (y2 - y1) / (x2 - x1);
// e mostramos o resultado
Memo1.Lines.Add('O coeficiente angular é: ' +
FloatToStr(m));
end;
Ao executar este código em linguagem Delphi nós teremos o seguinte resultado: O coeficiente angular é: 0,666666666666667 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
procedure TForm4.Button2Click(Sender: TObject);
var
x1, y1, x2, y2, tangente: Double;
cateto_oposto, cateto_adjascente, tetha: Double;
begin
// incluir a unit Math
// x e y do primeiro ponto
x1 := 3;
y1 := 6;
// x e y do segundo ponto
x2 := 9;
y2 := 10;
// vamos obter o comprimento do cateto oposto
cateto_oposto := y2 - y1;
// e agora o cateto adjascente
cateto_adjascente := x2 - x1;
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
tetha := ArcTan2(cateto_oposto, cateto_adjascente);
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
tangente := Tan(tetha);
// e mostramos o resultado
Memo1.Lines.Add('O coeficiente angular é: ' +
FloatToStr(tangente));
end;
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Java ::: Dicas & Truques ::: Imagens e Processamento de Imagens |
Como criar um programa de visualização de imagens em Java - Código fonte completoQuantidade de visualizações: 19558 vezes |
O que temos abaixo é o código completo para uma aplicação Java Swing que permite visualizar imagens JPG, GIF ou PNG. A imagem é selecinada usando um JFileChooser e carregada usando o método read() da classe ImageIO. Veja que usamos também uma classe personalizada de JPanel para exibir a imagem:
import java.awt.*;
import java.io.*;
import java.awt.image.*;
import java.awt.event.*;
import javax.swing.*;
import javax.imageio.*;
public class Estudos extends JFrame{
private BufferedImage imagem;
AreaImagem areaImagem;
public Estudos(){
super("Estudos Java");
Container c = getContentPane();
c.setLayout(new BorderLayout());
JButton btn = new JButton("Carregar Imagem");
btn.addActionListener(
new ActionListener(){
public void actionPerformed(ActionEvent e){
JFileChooser fc = new JFileChooser();
int res = fc.showOpenDialog(null);
if(res == JFileChooser.APPROVE_OPTION){
File arquivo = fc.getSelectedFile();
imagem = null;
try{
imagem = ImageIO.read(arquivo);
}
catch(IOException exc){
JOptionPane.showMessageDialog(null,
"Erro ao carregar a imagem: " +
exc.getMessage());
}
if(imagem != null){
areaImagem.imagem = imagem;
areaImagem.repaint();
}
}
}
}
);
c.add(btn, BorderLayout.SOUTH);
// Cria a área de exibição da imagem
areaImagem = new AreaImagem();
c.add(areaImagem, BorderLayout.CENTER);
setSize(400, 300);
setVisible(true);
}
public static void main(String args[]){
Estudos app = new Estudos();
app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
}
// Sub-classe de JPanel para exibir a imagem
class AreaImagem extends JPanel{
public BufferedImage imagem;
public void paintComponent(Graphics g){
super.paintComponent(g);
// desenha a imagem no JPanel
g.drawImage(imagem, 0, 0, this);
}
}
|
Java ::: Dicas & Truques ::: Data e Hora |
Como adicionar ou subtrair horas à data atual usando o método add() e a constante Calendar.HOUR da classe Calendar do JavaQuantidade de visualizações: 504 vezes |
Nesta dica mostrarei como podemos usar a função add() e a constante Calendar.HOUR da classe Calendar do Java para adicionar ou subtrair horas de uma data. Veja o exemplo a seguir:
package estudos;
import java.util.Calendar;
public class Estudos {
public static void main(String[] args) {
// vamos construir uma instância da classe Calendar
Calendar agora = Calendar.getInstance();
// vamos exibir a data e hora atuais
System.out.println("Data e hora atual: " +
agora.getTime().toString());
// adiciona 15 hora à hora atual
agora.add(Calendar.HOUR, 13);
// mostra a data e hora com as 15 horas adicionadas
System.out.println("Daqui a 15 horas: " +
agora.getTime().toString());
}
}
Ao executar este código Java nós teremos o seguinte resultado: Data e hora atual: Mon Jan 16 12:33:26 BRST 2023 Daqui a 15 horas: Tue Jan 17 01:33:26 BRST 2023 Se quisermos subtrair as horas ao invés de adicionar, basta fornecermos um valor negativo para o método add(). |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de Java - Como testar se um valor está contido em um array em JavaQuantidade de visualizações: 11300 vezes |
|
Pergunta/Tarefa: Escreva um programa Java GUI ou console que declara, constrói e inicializa um vetor (array unidimensional) de 5 inteiros. Em seguida peça ao usuário para informar um valor inteiro e informe se o valor lido está contido no vetor. A declaração, construção e inicialização do vetor pode ser feita da seguinte forma:
// declara, constrói e inicializa um vetor de 5 inteiros
int valores[] = {4, 21, 8, 120, 1};
Resposta/Solução: Veja a resolução comentada deste exercício usando Java console:
package estudos;
import javax.swing.JOptionPane;
public class Estudos {
public static void main(String[] args) {
// declara, constrói e inicializa um vetor de 5 inteiros
int valores[] = {4, 21, 8, 120, 1};
// vamos ler um valor inteiro
int pesquisa = Integer.parseInt(JOptionPane.showInputDialog("Valor:"));
// vamos verificar se o valor informado está contido no vetor
boolean encontrado = false;
for(int i = 0; i < valores.length; i++){
if(valores[i] == pesquisa){
encontrado = true;
break;
}
}
if(encontrado){
JOptionPane.showMessageDialog(null, "O valor está no vetor");
}
else{
JOptionPane.showMessageDialog(null, "O valor não está no vetor");
}
}
}
|
Python ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a equação reduzida da reta em Python dados dois pontos pertencentes à retaQuantidade de visualizações: 3276 vezes |
|
Nesta dica de Python veremos como calcular a equação reduzida da reta quando temos dois pontos pertencentes à esta reta. Não, nessa dica não vamos calcular a equação geral da reta, apenas a equação reduzida. Em outras dicas do site você encontra como como isso pode ser feito. Para relembrar: a equação reduzida da reta é y = mx + n, em que x e y são, respectivamente, a variável independente e a variável dependente; m é o coeficiente angular, e n é o coeficiente linear. Além disso, m e n são números reais. Com a equação reduzida da reta, é possível calcular quais são os pontos que pertencem a essa reta e quais não pertencem. Vamos começar então analisando a seguinte figura, na qual temos dois pontos que pertencem à uma reta: 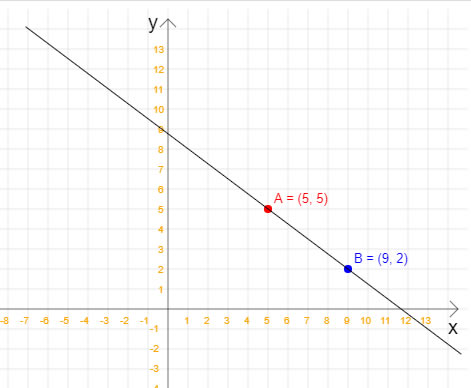 Note que a reta da figura passa pelos pontos A(5, 5) e B(9, 2). Então, uma vez que já temos os dois pontos, já podemos calcular a equação reduzida da reta. Veja o código Python completo para esta tarefa:
# método principal
def main():
# vamos ler as coordenadas do primeiro ponto
x1 = float(input("Coordenada x do primeiro ponto: "))
y1 = float(input("Coordenada y do primeiro ponto: "))
# vamos ler as coordenadas do segundo ponto
x2 = float(input("Coordenada x do segundo ponto: "))
y2 = float(input("Coordenada y do segundo ponto: "))
sinal = "+"
# vamos calcular o coeficiente angular da reta
m = (y2 - y1) / (x2 - x1)
# vamos calcular o coeficiente linear
n = y1 - (m * x1)
# coeficiente linear menor que zero? O sinal será negativo
if (n < 0):
sinal = "-"
n = n * -1
# mostra a equação reduzida da reta
print("Equação reduzida: y = %.2fx %s %.2f" % (m, sinal, n))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 5 Coordenada y do primeiro ponto: 5 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 2 Equação reduzida: y = -0,75x + 8,75 Para testarmos se nossa equação reduzida da reta está realmente correta, considere o valor 3 para o eixo x da imagem acima. Ao efetuarmos o cálculo: >> y = (-0.75 * 3) + 8.75 y = 6.5000 temos o valor 6.5 para o eixo y, o que faz com que o novo ponto caia exatamente em cima da reta considerada na imagem. |
Nossas 20 dicas & truques de programação mais populares |
Você também poderá gostar das dicas e truques de programação abaixo |
|
PHP - Como inserir um determinado número de zeros antes de um número em PHP usando a função sprintf() MySQL - Como adicionar uma chave primária a uma tabela MySQL usando o comando ALTER TABLE ADD PRIMARY KEY |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





