 |
|||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
|
|||||
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Recursão (Recursividade) |
Exercício Resolvido de Python - Um método recursivo que conta de 0 até 10Quantidade de visualizações: 1349 vezes |
|
Exercícios Resolvidos de Python - Um método recursivo que conta de 0 até 10 Pergunta/Tarefa: Escreva um método recursivo que conta e exibe os valores de 0 até 10. Seu método deverá possuir a seguinte assinatura: def contar_recursivamente(n): # sua implementação aqui Sua saída deverá ser parecida com: 0 1 2 3 4 5 6 7 8 9 10 Veja a resolução comentada deste exercício usando Python:
# método recursivo que conta de 0 até 10
def contar_recursivamente(n):
# vamos exibir o número atual
print(n, " ", end =" ")
# devemos prosseguir com a recursividade?
if n < 10:
# incrementa o valor de n
n = n + 1
contar_recursivamente(n) # e faz uma nova chamada recursiva
# método principal
def main():
# efetua uma chamada ao método recursivo fornecendo o primeiro valor
contar_recursivamente(0)
if __name__== "__main__":
main()
|
Python ::: Fundamentos da Linguagem ::: Passos Iniciais |
Como criar módulos de código reutilizável em PythonQuantidade de visualizações: 8696 vezes |
|
Uma das características da boa programação é reutilizar ao máximo códigos bem testados e independentes. A criação de módulos de funções e definições de classes em Python pode ser feita de forma bem simples. 1) Comece criando um arquivo chamado funcoes.py com o seguinte conteúdo: """ Sou um módulo Python. A única funcionalidade que ofereço é uma função que soma dois números """ def somar(num1, num2): return (num1 + num2) 2) Salve este arquivo no diretório atual de sua aplicação e vamos importá-lo. Para isso escreva um novo programa. Uma sugestão é:
"""
Sou o programa principal e vou importar
o módulo que contém a função somar
"""
import funcoes
def main():
print(funcoes.somar(3, 5))
if __name__== "__main__":
main()
3) Execute o programa e veja o resultado. Para que este programa funcione corretamente, é preciso que o módulo a ser importado esteja no diretório atual ou em qualquer um dos diretórios pesquisados pelo interpretador Python, geralmente representados pelo variável de ambiente PYTHONPATH. Porém, há situações que queremos agrupar nossos módulos em um diretório dentro do diretório principal da aplicação. O exemplo abaixo mostra como importar um módulo localizado no diretório "lib" da aplicação atual: """ Sou o programa principal e vou importar o módulo que contém a função somar() """ # importa o módulo sys import sys # acrescenta o diretório lib na variável # de ambiente PYTHONPATH sys.path.append(sys.path[0] + '\\lib') # pode importar funcoes no diretório lib import funcoes # pode chamar o método somar agora def main(): print(funcoes.somar(3, 5)) if __name__== "__main__": main() |
C ::: C para Engenharia ::: Física - Mecânica |
Como calcular Velocidade Vetorial Média usando a linguagem C - C para Engenharia - Física - Mecânica - CinemáticaQuantidade de visualizações: 3045 vezes |
|
Como calcular Velocidade Vetorial Média usando a linguagem C Na Física, mais especificamente na Mecânica e Cinemática, nós estamos o tempo todo interessados em medir a "rapidez" com que uma partícula se move de um ponto para outro ponto. Por partícula podemos entender qualquer móvel: um carro, um avião, uma bola, uma pessoa, etc. No caso de um movimento bidimensional ou tridimensional nós devemos considerar a grandeza velocidade média como vetores e usar a notação vetorial. Em outras dicas do site você encontrará cálculos envolvendo vetores e até mesmo calculadoras com as operações vetoriais mais comuns. Dessa forma, a fórmula para obtenção da Velocidade Vetorial Média é: \[\vec{v}_\text{méd} = \frac{\Delta \vec{r}}{\Delta t} \] Onde __$\Delta \vec{r}__$ é a variação da posição da partícula e __$\Delta t__$ é a variação do tempo entre os dois deslocamentos cuja velocidade vetorial média querermos medir. Antes de vermos o código C, dê uma boa olhada na imagem a seguir: 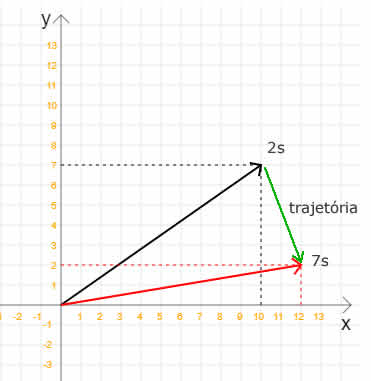 Nosso objetivo será calcular a velocidade vetorial média da partícula saindo da posição __$\vec{r}_1__$ = 10__$\hat{\imath}__$ + 7__$\hat{\jmath}__$ m (10, 7), no instante t1 = 2s, e indo para a posição __$\vec{r}_2__$ = 12__$\hat{\imath}__$ + 2__$\hat{\jmath}__$ m (12, 2) em t2 = 7s. Note que o trajeto da partícula foi marcado de verde na imagem. E agora, finalmente, vamos ao código C que lê os valores das coordenadas x e y dos dois vetores de posições (inicial e final), o tempo de deslocamento inicial e final e mostra o vetor velocidade média:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
// coordenadas dos dois vetores de posições
float x1, y1, x2, y2;
// guarda o vetor delta r (variação do deslocamento)
float delta_r_x, delta_r_y;
// guarda o tempo inicial, tempo final e variacao (em segundos)
float tempo_inicial, tempo_final, delta_t;
// guarda as coordenadas do vetor velocidade
float vetor_vm_x, vetor_vm_y;
// x e y do primeiro vetor
printf("Coordenada x do primeiro vetor: ");
scanf("%f", &x1);
printf("Coordenada y do primeiro vetor: ");
scanf("%f", &y1);
// x e y do segundo vetor
printf("Coordenada x do segundo vetor: ");
scanf("%f", &x2);
printf("Coordenada y do segundo vetor: ");
scanf("%f", &y2);
// vamos ler o tempo inicial e tempo final
printf("Tempo inicial em segundos: ");
scanf("%f", &tempo_inicial);
printf("Tempo final em segundos: ");
scanf("%f", &tempo_final);
// vamos calcular o vetor delta r
delta_r_x = x2 - x1;
delta_r_y = y2 - y1;
// vamos calcular o delta t (variação do tempo)
delta_t = tempo_final - tempo_inicial;
// finalmente calculamos o vetor velocidade média
vetor_vm_x = delta_r_x / delta_t;
vetor_vm_y = delta_r_y / delta_t;
// mostramos o resultado
printf("O Vetor Velocidade Média é: (%.2f, %.2f)m/s",
vetor_vm_x, vetor_vm_y);
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: Coordenada x do primeiro vetor: 10 Coordenada y do primeiro vetor: 7 Coordenada x do segundo vetor: 12 Coordenada y do segundo vetor: 2 Tempo inicial em segundos: 2 Tempo final em segundos: 7 O Vetor Velocidade Média é: (0.40, -1.00)m/s Pressione qualquer tecla para continuar. . . Note que aqui nós estamos usando vetores do R2, mas o processo é o mesmo para vetores do R3. |
Java ::: Fundamentos da Linguagem ::: Tipos de Dados |
Java para iniciantes - Como usar o tipo de dados short da linguagem JavaQuantidade de visualizações: 12175 vezes |
O tipo de dados short pode ser usado quando queremos armazenar valores inteiros na faixa -32,768 à 32,767. Veja um exemplo:
public class Estudos{
static short valor = 30000;
public static void main(String args[]){
System.out.println("O valor da variável é: "
+ valor);
System.exit(0);
}
}
Porém, é preciso estar atento a um detalhe muito importante (testado na versão 6 do SDK). Veja o trecho de código seguinte:
public class Estudos{
public static void main(String args[]){
short a = 32;
short b = 19;
short soma = a + b;
System.out.println("O resultado é: " + soma);
System.exit(0);
}
}
À primeira vista este código está correto, visto que a soma das variáveis a e b não ultrapassam a faixa do tipo short. Porém, ao tentarmos compilar, temos a seguinte mensagem de erro:
Estudos.java:5: possible loss of precision
found : int
required: short
short soma = a + b;
^
1 error
short a = 32; short b = 19; short soma = (short)(a + b); O tipo de dados short pode ser convertido (sem a necessidade de cast) para os seguintes tipos: short -> int -> long -> float -> double Se precisarmos converter o tipo short para os tipos char e byte, teremos que lançar mão de uma coerção (cast). Veja: short a = 32; short b = 19; byte soma = (byte)(a + b); |
C ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Como usar a instrução break da linguagem C para interromper a execução de um laçoQuantidade de visualizações: 15756 vezes |
Laços for, while, do...while e switch podem ter suas iterações (repetições) interrompidas com o uso da instrução break. Quando isso acontece, o fluxo de execução salta para a primeira instrução após o laço. Veja um exemplo:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[])
{
int i;
for(i = 0; i <= 10; i++){
printf("%d ", i);
if(i == 6)
break; // sai do laço
}
printf("\n\n");
system("PAUSE");
return 0;
}
Este código exibirá os valores de 0 à 6. Veja que execução do laço é interrompida exatamente no ponto em que a instrução break é encontrada. Se houver mais instruções dentro do laço mas logo após o break, estas instruções não serão executadas. |
C ::: C para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular a norma ou módulo de vetores nos espaços R2 e R3 usando C - Geometria Analítica e Álgebra Linear usando CQuantidade de visualizações: 4416 vezes |
|
Em Geometria Analítica e Álgebra Linear, a magnitude, norma, comprimento, tamanho ou módulo (também chamado de intensidade na Física) de um vetor é o seu comprimento, que pode ser calculado por meio da distância de seu ponto final a partir da origem, no nosso caso (0,0). Considere o seguinte vetor no plano, ou seja, no espaço bidimensional, ou R2: \[\vec{v} = \left(7, 6\right)\] Aqui este vetor se inicia na origem (0, 0) e vai até as coordenadas (x = 7) e (y = 6). Veja sua plotagem no plano 2D:  Note que na imagem já temos todas as informações que precisamos, ou seja, o tamanho desse vetor é 9 (arredondado) e ele faz um ângulo de 41º (graus) com o eixo x positivo. Em linguagem mais adequada da trigonometria, podemos dizer que a medida do cateto oposto é 6, a medida do cateto adjacente é 7 e a medida da hipotenusa (que já calculei para você) é 9. Note que já mostrei também o ângulo theta (__$\theta__$) entre a hipotenusa e o cateto adjacente, o que nos dá a inclinação da reta representada pelos pontos (0, 0) e (7, 6). Relembrando nossas aulas de trigonometria nos tempos do colegial, temos que o quadrado da hipotenusa é a soma dos quadrados dos catetos, ou seja, o Teorema de Pitágoras: \[a^2 = b^2 + c^2\] Como sabemos que a potenciação é o inverso da radiciação, podemos escrever essa fórmula da seguinte maneira: \[a = \sqrt{b^2 + c^2}\] Passando para os valores x e y que já temos: \[a = \sqrt{7^2 + 6^2}\] Podemos comprovar que o resultado é 9,21 (que arredondei para 9). Não se esqueça da notação de módulo ao apresentar o resultado final: \[\left|\vec{v}\right| = \sqrt{7^2 + 6^2}\] E aqui está o código C que nos permite informar os valores x e y do vetor e obter o seu comprimento, tamanho ou módulo:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(int argc, char *argv[]){
float x, y, norma;
// vamos ler os valores x e y
printf("Informe o valor de x: ");
scanf("%f", &x);
printf("Informe o valor de y: ");
scanf("%f", &y);
// vamos calcular a norma do vetor
norma = sqrt(pow(x, 2) + pow(y, 2));
// mostra o resultado
printf("A norma do vetor é: %f", norma);
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: Informe o valor de x: 7 Informe o valor de y: 6 A norma do vetor é: 9.219544457292887 Novamente note que arredondei o comprimento do vetor para melhor visualização no gráfico. Para calcular a norma de um vetor no espaço, ou seja, no R3, basta acrescentar o componente z no cálculo. |
Python ::: Python para Engenharia ::: Engenharia Civil - Cálculo Estrutural |
Como calcular a Força Normal Adimensional ou Força Normal Reduzida de um pilar em Python - Python para Estruturas de Concreto ArmadoQuantidade de visualizações: 507 vezes |
 A Força Normal Adimensional de um pilar, também chamada de Força Normal Reduzida, é representada pela letra grega ν (ni) e nos dá uma idéia da magnitude da força normal que está sendo aplicada na seção transversal de um pilar. A fórmula para o cálculo da Força Normal Adimensional pode ser representada da seguinte forma: \[\nu = \frac{N_\text{sd}}{A_\text{c} \cdot \frac{f_\text{ck}}{\gamma _\text{c}}} \] Onde: ν é a Força Normal Adimensional sem unidade; Nd é a força normal de projeto, em kN. fck é a resistência característica do concreto em kN/cm2. Para converter de Mpa para kN/cm2 nós só precisamos dividir por 10. γc é o fator de ponderação do concreto e, em geral, possui o valor 1,4. Ao dividirmos o fck pelo γc nós chegamos ao fcd, que é resistência de cálculo do concreto. Note que o valor encontrado para a força normal adimensional ν (ni) é o valor que, junto com o μ (mi), forma a dupla de fatores para o ábaco de VENTURINI que nos retornará o valor de ω (ômega) que nos ajudará a calcular a área de aço (As) do pilar. Há duas considerações importantes em relação à Força Normal Adimensional ν de um pilar: a) Se ν < 0,30 -> pode ser adequado reduzir a seção transversal do pilar. b) Se ν > 1,30 -> pode ser conveniente aumentar a seção transversal do pilar. Agora vamos ver o código Python? Note que pediremos para o usuário informar as dimensões do pilar nas direções x e y em centímetros, a carga total no pilar em kN e o fck do concreto em Mpa e retornaremos o valor da força normal adimensional:
# método principal
def main():
# vamos pedir as dimensões do pilar
hx = float(input("Informe a dimensão do pilar na direção x (em cm): "))
hy = float(input("Informe a dimensão do pilar na direção y (em cm): "))
# vamos pedir a carga total no pilar em kN
Nk = float(input("Informe a carga total no pilar (em kN): "))
# agora vamos obter o FCK do concreto em MPa
fck = float(input("Informe o FCK do concreto (em MPa): "))
# vamos converter MPa para kN/cm2
fck = fck / 10
# vamos obter o menor lado do pilar (menor dimensão da seção transversal)
if (hx < hy):
b = hx
else:
b = hy
# agora vamos calcular a área do pilar em centímetros quadrados
area = hx * hy
# a área está de acordo com a norma NBR 6118 (ABNT, 2014)
if (area < 360):
print("A área do pilar não pode ser inferior a 360cm2")
return
# vamos calcular a força normal de projeto Nd
yn = 1.95 - (0.05 * b) # de acordo com a norma NBR 6118 (ABNT, 2014) Tabela 13.1
yf = 1.4 # regra geral para concreto armado
Nd = yn * yf * Nk
# vamos fixar o fator de ponderação do concreto em 1.4
yc = 1.4
# e agora calculamos a força normal adimensional do pilar
fna = Nd / (area * (fck / yc))
# e mostramos o resultado
print("\nA Força Normal Adimensional do pilar é: {0}".format(round(fna, 2)))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Informe a dimensão do pilar na direção x (em cm): 40 Informe a dimensão do pilar na direção y (em cm): 19 Informe a carga total no pilar (em kN): 841.35 Informe o FCK do concreto (em MPa): 30 A Força Normal Adimensional do pilar é: 0.72 |
Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular a distância entre dois pontos no plano em Python - Python para Geometria Analítica e Álgebra LinearQuantidade de visualizações: 10662 vezes |
|
Como calcular a Distância Euclidiana entre dois pontos usando Python. Em várias aplicações envolvendo geometria, principalmente no desenvolvimento de jogos em Python, é comum nos depararmos com a necessidade de calcular a distância entre dois pontos A e B. Nessa dica mostrarei como efetuar esse cálculo no R2, ou seja, no plano. Em outra dica eu abordo o cálculo no R3 (espaço). Comece analisando a imagem abaixo:  Veja que temos um ponto A (x = 3; y = 6) e um ponto B (x = 9; y = 4). Para determinarmos a distância entre esses dois pontos no plano cartesiano, temos que realizar a análise tanto no sentido do eixo das abscissas (x) quanto no do eixo das ordenadas (y). Veja a fórmula: \[d_{AB} = \sqrt{\left(x_b - x_a\right)^2 + \left(y_b - y_a\right)^2}\] Agora, jogando os valores dos dois pontos da fórmula nós teremos: \[d_{AB} = \sqrt{\left(9 - 3\right)^2 + \left(6 - 4\right)^2}\] Que resulta em 6,32 (aproximadamente). E agora veja o código Python completo que lê as coordenadas dos dois pontos e mostra a distância entre eles:
import math
# função que permite calcular a distância
# entre dois pontos no plano (R2)
def distancia2d(x1, y1, x2, y2):
a = x2 - x1
b = y2 - y1
c = math.sqrt(math.pow(a, 2) + math.pow(b, 2))
return c
# função principal do programa
def main():
# vamos ler os dados do primeiro ponto
x1 = float(input("Informe o x do primeiro ponto: "))
y1 = float(input("Informe o y do primeiro ponto: "))
# vamos ler os dados do segundo ponto
x2 = float(input("Informe o x do segundo ponto: "))
y2 = float(input("Informe o y do segundo ponto: "))
# vamos obter a distância entre eles
distancia = distancia2d(x1, y1, x2, y2)
print("Distância entre os dois pontos: %0.2f" % distancia);
if __name__== "__main__":
main()
Ao executarmos este código Python nós teremos o seguinte resultado: Informe o x do primeiro ponto: 3 Informe o y do primeiro ponto: 6 Informe o x do segundo ponto: 9 Informe o y do segundo ponto: 4 Distância entre os dois pontos: 6.32 |
GoLang ::: Fundamentos da Linguagem ::: Laços de Repetição |
Como usar o laço for em GoLang - O laço for da linguagem GoQuantidade de visualizações: 1012 vezes |
|
Como todas (ou praticamente todas) as linguagens de programação, a GoLang também possui o seu laço for, ou loop for. Este laço é usado para repetir uma ou mais instruções quando sabemos exatamente quantas vezes essa repetição ocorrerá. Em Go, o laço for é composto de três partes: inicialização, teste de continuidade e incremento ou decremento da variável de controle. Na parte da inicialização nós declaramos e inicializamos as variáveis que serão usadas dentro da estrutura. O teste de continuidade é a parte na qual verificamos se o laço deverá continuar repetindo ou encerrar. Finalmente, a parte de incremento ou decremento é usada para ajustarmos a variável de controle do laço. Veja, por exemplo, como escrever um laço for em GoLang que contará de 1 até 10, escrevendo os números na tela:
// pacote principal
package main
// vamos importar o módulo de formatação de
// entrada e saída
import "fmt"
// esta é a função principal do programa
func main() {
for i := 1; i <= 10; i++ {
fmt.Printf("%d ", i)
}
}
Ao executar este código Go nós teremos o seguinte resultado: 1 2 3 4 5 6 7 8 9 10 O laço for da linguagem GoLang nos permite omitir as partes da inicialização e de incremento ou decremento, embora esse tipo de código não seja muito usual. Veja um trecho de código no qual usamos o laço for da linguagem Go para contar de 10 até 0 (omitindo a parte da inicialização da variável de controle):
// pacote principal
package main
// vamos importar o módulo de formatação de
// entrada e saída
import "fmt"
// esta é a função principal do programa
func main() {
i := 10 // definimos o valor inicial aqui
for ; i >= 0; i-- {
fmt.Printf("%d ", i)
}
}
Ao executarmos este código Go nós teremos o seguinte resultado: 10 9 8 7 6 5 4 3 2 1 0 Veja, agora, uma modificação do código acima. Desta vez eu omiti a parte de incremento ou decremento da variável de controle:
// pacote principal
package main
// vamos importar o módulo de formatação de
// entrada e saída
import "fmt"
// esta é a função principal do programa
func main() {
for i := 10; i >= 0; {
fmt.Printf("%d ", i)
i--
}
}
|
C# ::: Coleções (Collections) ::: List<T> |
Como pesquisar um elemento em uma lista do C# usando a função Find() e um PredicateQuantidade de visualizações: 15142 vezes |
|
Em algumas situações gostaríamos de pesquisar e retornar o primeiro elemento de uma List<T> que obedece a algum critério de busca. Assim, poderíamos, por exemplo, pesquisar um nome que começa com uma determinada palavra ou um preço de produto maior ou igual a um determinado valor. Para tais situações podemos usar o método Find(). Este método possui a seguinte assinatura: public T Find( Predicate<T> match ) Veja que o método pede um delegate do tipo Predicate<T> que define as condições para a pesquisa do elemento. Se o elemento for encontrado, este é retornado. Caso contrário, o valor padrão para T é retornado (null para referências). Veja um trecho de código no qual eu mostro como usar o método Find() em combinação com um método personalizado que permite usar um delegate anônimo. Desta forma conseguimos fornecer, em tempo de execução, o argumento para o parâmetro match do Predicate:
static void Main(string[] args){
// vamos criar um objeto da classe List<T>
List<string> nomes = new List<string>();
// vamos inserir quatro valores na lista
nomes.Add("Osmar J. Silva");
nomes.Add("Salvador Miranda de Andrade");
nomes.Add("Dyego Fernandes de Souza");
nomes.Add("Marcos de Paula Rocha");
// vamos pesquisar um valor na lista usando um método personalizado
// Neste exemplo vamos retornar o primeiro nome que contenha a palavra
// "Dyego"
string nome = encontrar(nomes, "Dyego");
// vamos verificar se o nome foi encontrado
if(nome != null){
// foi encontrado....vamos retornar o resultado
Console.WriteLine(nome);
}
else{
Console.WriteLine("Nenhum nome encontrado.");
}
// vamos pausar a execução
Console.Write("\n\nPressione qualquer tecla para continuar...");
Console.ReadKey();
}
// método auxiliar que permite encontrar um valor na lista usando
// o método Find() da classe List<T> e um Predicate
static string encontrar(List<string> lista, string texto){
string encontrado = null;
// vamos pesquisar o valor na lista usando seu método Find()
// Aqui o primeiro nome que passar no critério de busca será retornado
encontrado = lista.Find(delegate(string valor){
return valor.Contains(texto);
});
return encontrado;
}
O método Find() executa uma busca linear. Assim, este método é uma operação O(n), onde n é a quantidade de elementos na lista. |
Nossas 20 dicas & truques de programação mais populares |
|
Delphi - Como calcular MDC em Delphi |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Java - Como usar a classe Character da linguagem Java para tratar caracteres individuais em seus programas Java - Estruturas de Dados em Java - Como obter o nó com menor valor em uma árvore binária de busca em Java MySQL - Como formatar campos DATE, TIME, DATETIME e TIMESTAMP usando a função DATE_FORMAT() do MySQL |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




