 |
|||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
|
|||||
C ::: Dicas & Truques ::: Arquivos e Diretórios |
Como testar se um arquivo existe usando a linguagem CQuantidade de visualizações: 14322 vezes |
Muitas vezes precisamos saber se um determinado arquivo existe antes de efetuarmos alguma operação. O trecho de código abaixo mostra como você pode implementar uma função file_exists() em C que pode ser usada em seus programas. O segredo aqui é tentar abrir o arquivo passado como argumento para a função. Se o arquivo for aberto com sucesso, sabemos que ele existe e a função retorna o valor 1 (true), do contrário retorna 0 (false):
#include <stdio.h>
#include <stdlib.h>
/*
Implementação de uma função file_exists() em C. Se
o arquivo existir o valor 1 (true) será retornado. Caso
contrário a função retornará 0 (false).
*/
int file_exists(const char *filename)
{
FILE *arquivo;
if(arquivo = fopen(filename, "r"))
{
fclose(arquivo);
return 1;
}
return 0;
}
int main(int argc, char *argv[])
{
// testa se o arquivo existe
if(file_exists("c:\\testes.txt")){
printf("O arquivo existe no local especificado.\n");
}
else
printf("O arquivo NAO existe no local especificado.\n");
printf("\n\n");
system("PAUSE");
return 0;
}
|
Ruby ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de Ruby - Escreva um programa Ruby para mover todos os zeros para o final do vetor, sem alterar a ordem dos elementos já presentes no arrayQuantidade de visualizações: 1241 vezes |
|
Pergunta/Tarefa: Dado o seguinte vetor de inteiros: # vamos declarar e construir um vetor de 8 inteiros valores = [0, 3, 0, 5, 7, 4, 0, 9] Sua saída deverá ser parecida com: Vetor na ordem original: 0 3 0 5 7 4 0 9 Vetor com os zeros deslocados para o final: 3 5 7 4 9 0 0 0 Veja a resolução comentada deste exercício usando Ruby:
# vamos declarar e construir um vetor de 8 inteiros
valores = [0, 3, 0, 5, 7, 4, 0, 9]
# vamos mostrar o vetor na ordem original
print("Vetor na ordem original:\n")
for i in (0..valores.length - 1)
printf("%d ", valores[i])
end
# vamos inicializar j como 0 para que ele aponte para
# o primeiro elemento do vetor
j = 0
# agora o laço for percorre todos os elementos do vetor,
# incrementanto a variável i e deixando o j em 0
for i in (0..valores.length - 1)
# encontramos um valor que não é 0
if(valores[i] != 0)
# fazemos a troca entre os elementos nos índices
# i e j
temp = valores[i]
valores[i] = valores[j]
valores[j] = temp
# e avançamos o j para o elemento seguinte
j = j + 1
end
end
# agora mostramos o resultado
print("\n\nVetor com os zeros deslocados para o final:\n")
for i in (0..valores.length - 1)
printf("%d ", valores[i])
end
Não se esqueça: A resolução do exercício deve ser feita sem a criação de um vetor, array ou lista adicional, e os elementos diferentes de zero devem permanecer na mesma ordem que eles estavam antes. |
Java ::: Java para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como converter Coordenadas Cartesianas para Coordenadas Polares usando Java - Java para EngenhariaQuantidade de visualizações: 2210 vezes |
|
Nesta nossa série de Java para Geometria Analítica e Álgebra Linear, mostrarei um código 100% funcional para fazer a conversão entre coordenadas cartesianas e coordenadas polares. Esta operação é muito frequente em computação gráfica e é parte integrante das disciplinas dos cursos de Engenharia (com maior ênfase na Engenharia Civil). Na matemática, principalmente em Geometria e Trigonometria, o sistema de Coordenadas no Plano Cartesiano, ou Espaço Cartesiano, é um sistema que define cada ponto em um plano associando-o, unicamente, a um conjuntos de pontos numéricos. Dessa forma, no plano cartesiano, um ponto é representado pelas coordenadas (x, y), com o x indicando o eixo horizontal (eixo das abscissas) e o y indicando o eixo vertical (eixo das ordenadas). Quando saímos do plano (espaço 2D ou R2) para o espaço (espaço 3D ou R3), temos a inclusão do eixo z (que indica profundidade). Já o sistema de Coordenadas Polares é um sistema de coordenadas em duas dimensões no qual cada ponto no plano é determinado por sua distância a partir de um ponto de referência conhecido como raio (r) e um ângulo a partir de uma direção de referência. Este ângulo é normalmente chamado de theta (__$\theta__$). Assim, um ponto em Coordenadas Polares é conhecido por sua posição (r, __$\theta__$). Antes de prosseguirmos, veja uma imagem demonstrando os dois sistemas de coordenadas: 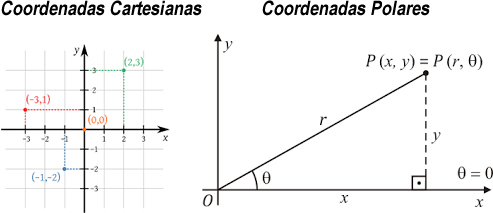 A fórmula para conversão de Coordenadas Cartesianas para Coordenadas Polares é: __$r = \sqrt{x^2+y2}__$ __$\theta = \\arctan\left(\frac{y}{x}\right)__$ E aqui está o código Java completo que recebe as coordenadas cartesianas (x, y) e retorna as coordenadas polares (r, __$\theta__$):
package arquivodecodigos;
import java.util.Scanner;
public class Estudos{
public static void main(String args[]){
Scanner entrada = new Scanner(System.in);
// vamos ler as coordenadas cartesianas
System.out.print("Valor de x: ");
double x = Double.parseDouble(entrada.nextLine());
System.out.print("Valor de y: ");
double y = Double.parseDouble(entrada.nextLine());
// vamos calcular o raio
double raio = Math.sqrt(Math.pow(x, 2) + Math.pow(y, 2));
// agora calculamos o theta (ângulo) em radianos
double theta = Math.atan2(y, x);
// queremos o ângulo em graus também
double angulo_graus = 180 * (theta / Math.PI);
// e exibimos o resultado
System.out.println("As Coordenadas Polares são:\n" +
"raio = " + raio + ", theta = " + theta + ", ângulo em graus = " +
angulo_graus);
}
}
Ao executar este código nós teremos o seguinte resultado: Valor de x: -1 Valor de y: 1 As Coordenadas Polares são: raio = 1.4142135623730951, theta = 2.356194490192345, ângulo em graus = 135.0 Veja que as coordenadas polares equivalentes são (__$\sqrt{2}__$, __$\frac{3\pi}{4}__$), com o theta em radianos. Sim, os professores das disciplinas de Geometria Analítica e Álgebra Linear, Física e outras gostam de escrever os resultados usando raizes e frações em vez de valores reais. |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de Java - Como verificar quantas vezes um valor é encontrado em um vetor - Como usar vetores e matrizes em JavaQuantidade de visualizações: 16218 vezes |
|
Pergunta/Tarefa: Escreva um programa Java que declara, constrói e inicializa um vetor de 10 inteiros. Em seguida peça para que o usuário informe um valor a ser pesquisado. Faça uma varredura no vetor e informe quantas vezes o valor pesquisado é encontrado:
// declara, constrói e inicializa um vetor de 10 inteiros
int valores[] = {4, 21, 9, 8, 12, 21, 4, 4, 1, 10};
Informe um valor: 4 O valor foi encontrado: 3 vezes Informe um valor: 8 O valor foi encontrado: 1 vezes Informe um valor: 3 O valor foi encontrado: 0 vezes Veja a resolução comentada deste exercício usando Java:
package estudos;
import java.util.Scanner;
public class Estudos{
public static void main(String[] args){
// declara, constrói e inicializa um vetor de 10 inteiros
int valores[] = {4, 21, 9, 8, 12, 21, 4, 4, 1, 10};
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// vamos ler um valor inteiro
System.out.print("Informe um valor: ");
int pesquisa = Integer.parseInt(entrada.nextLine());
// vamos verificar quantas vezes o valor informado está
// contido no vetor
int repeticoes = 0;
for(int i = 0; i < valores.length; i++){
if(valores[i] == pesquisa){
repeticoes++; // encontrou? vamos contar esta ocorrência
}
}
// vamos mostrar o resultado
System.out.println("O valor foi encontrado: " +
repeticoes + " vezes");
}
}
|
LISP ::: LISP para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como converter Coordenadas Cartesianas para Coordenadas Polares em LISP - LISP para EngenhariaQuantidade de visualizações: 806 vezes |
|
Nesta nossa série de LISP e AutoLISP para Geometria Analítica e Álgebra Linear, mostrarei um código 100% funcional para fazer a conversão entre coordenadas cartesianas e coordenadas polares. Esta operação é muito frequente em computação gráfica e é parte integrante das disciplinas dos cursos de Engenharia (com maior ênfase na Engenharia Civil). Na matemática, principalmente em Geometria e Trigonometria, o sistema de Coordenadas no Plano Cartesiano, ou Espaço Cartesiano, é um sistema que define cada ponto em um plano associando-o, unicamente, a um conjuntos de pontos numéricos. Dessa forma, no plano cartesiano, um ponto é representado pelas coordenadas (x, y), com o x indicando o eixo horizontal (eixo das abscissas) e o y indicando o eixo vertical (eixo das ordenadas). Quando saímos do plano (espaço 2D ou R2) para o espaço (espaço 3D ou R3), temos a inclusão do eixo z (que indica profundidade). Já o sistema de Coordenadas Polares é um sistema de coordenadas em duas dimensões no qual cada ponto no plano é determinado por sua distância a partir de um ponto de referência conhecido como raio (r) e um ângulo a partir de uma direção de referência. Este ângulo é normalmente chamado de theta (__$\theta__$). Assim, um ponto em Coordenadas Polares é conhecido por sua posição (r, __$\theta__$). Antes de prosseguirmos, veja uma imagem demonstrando os dois sistemas de coordenadas:  A fórmula para conversão de Coordenadas Cartesianas para Coordenadas Polares é: __$r = \sqrt{x^2+y2}__$ __$\theta = \\arctan\left(\frac{y}{x}\right)__$ E aqui está o código LISP completo que recebe as coordenadas cartesianas (x, y) e retorna as coordenadas polares (r, __$\theta__$):
; programa LISP que converte Coordenadas Cartesianas
; em Coordenadas Polares
(let((x)(y)(raio)(theta)(angulo_graus))
; vamos ler as coordenadas cartesianas
(princ "Valor de x: ")
(force-output)
(setq x (read))
(princ "Valor de y: ")
(force-output)
(setq y (read))
; vamos calcular o raio
(setq raio (sqrt (+ (expt x 2) (expt y 2))))
; agora calculamos o theta (ângulo) em radianos
(setq theta (atan y x))
; queremos o ângulo em graus também
(setq angulo_graus (* 180 (/ theta pi)))
; e exibimos o resultado
(princ "As Coordenadas Polares são: ")
(format t "raio = ~F, theta = ~F, ângulo em graus: ~F"
raio theta angulo_graus)
)
Ao executar este código LISP nós teremos o seguinte resultado: Valor de x: -1 Valor de y: 1 As Coordenadas Polares são: raio = 1.4142135623730951, theta = 2.356194490192345, ângulo em graus = 135.0 Veja que as coordenadas polares equivalentes são (__$\sqrt{2}__$, __$\frac{3\pi}{4}__$), com o theta em radianos. Sim, os professores das disciplinas de Geometria Analítica e Álgebra Linear, Física e outras gostam de escrever os resultados usando raizes e frações em vez de valores reais. |
Java ::: Fundamentos da Linguagem ::: Tipos de Dados |
Como usar null em JavaQuantidade de visualizações: 32046 vezes |
|
O tipo de dados null é um tipo (ou valor) especial que indica que uma referência não está apontando para nenhum objeto, ou seja, aponta para uma posição de memória nula. Este tipo pode ser atribuído (ou testado) apenas a referências. Seu uso não é permitido com primitivos. Veja um trecho de código no qual definimos que uma variável do tipo String aponta para um objeto nulo:
public class Estudos{
public static void main(String args[]){
String nome = null;
System.out.println(nome.length());
System.exit(0);
}
}
Este código compila normalmente. Porém, ao tentarmos executá-lo, temos uma exceção de tempo de execução NullPointerException: Exception in thread "main" java.lang.NullPointerException at Estudos.main(Estudos.java:5) Isso aconteceu porque estamos tentando executar um método de um objeto que não existe. Uma técnica muito valiosa é testar se uma referência não está apontando para um objeto nulo. Veja como isso é feito:
public class Estudos{
public static void main(String args[]){
String nome = null;
if(nome != null)
System.out.println(nome.length());
else
System.out.println("Objeto é nulo.");
System.exit(0);
}
}
Tenha em mente que, quando uma referência recebe o valor null, o objeto para o qual ela apontava fica imediatamente disponível para o coletor de lixo (Garbagge Colector), ou seja, a memória ocupada pelo objeto pode ser liberada a qualquer momento. Veja agora o que acontece quando tentamos atribuir o valor null a um primitivo:
public class Estudos{
public static void main(String args[]){
int valor = null;
System.exit(0);
}
}
Eis a mensagem de erro de compilação:
Estudos.java:3: incompatible types
found : <nulltype>
required: int
int valor = null;
^
1 error
|
Java ::: Pacote java.awt ::: Graphics |
Como retornar a cor atual do contexto de desenho usando o método getColor() da classe Graphics do Java - Computação gráfica em JavaQuantidade de visualizações: 7996 vezes |
|
Antes de efetuar qualquer desenho na superfície de um componente, é importante saber qual cor está definida no momento, assim podemos alterá-la se necessário. Para isso podemos usar o método getColor() da classe Graphics. Este método retorna um objeto da classe Color. Veja um exemplo no qual obtemos a cor usada atualmente para desenhar na superfície de um JLabel:
import java.awt.*;
import java.awt.event.*;
import javax.swing.*;
public class Estudos extends JFrame{
JLabel label;
public Estudos() {
super("Desenhando");
Container c = getContentPane();
c.setLayout(new BorderLayout());
// Cria um JLabel
label = new JLabel();
c.add(label, BorderLayout.CENTER);
// Cria um botão
JButton btn = new
JButton("Obter a cor do contexto");
btn.addActionListener(
new ActionListener(){
public void actionPerformed(ActionEvent e){
Graphics graphics = label.getGraphics();
// obtém a cor usada para desenhar no
// contexto de desenho
Color cor = graphics.getColor();
JOptionPane.showMessageDialog(null,
"A cor usada atualmente é " +
cor.toString());
}
}
);
// Adiciona o botão à janela
c.add(btn, BorderLayout.SOUTH);
setSize(350, 250);
setVisible(true);
}
public static void main(String args[]){
Estudos app = new Estudos();
app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
}
Ao executar este código Java nós teremos o seguinte resultado: A cor usada atualmente é java.awt.Color[r=0,g=0,b=0] |
Java ::: Dicas & Truques ::: Matemática e Estatística |
Como calcular porcentagem em Java - Como efetuar cálculos de porcentagem em JavaQuantidade de visualizações: 55356 vezes |
|
Cálculos de porcentagens estão presentes em boa parte das aplicações que desenvolvemos. Porém, há momentos em que a mente trava e não conseguimos lembrar com clareza como estes cálculos são feitos, principalmente em Java. Esta anotação tem o objetivo de ser uma fonte de pesquisa para os momentos em que suas habilidades matemáticas insistirem em continuar ocultas. Ex: 1 - Suponhamos que um produto que custe R$ 178,00 sofra um acréscimo de 15%. Qual o valor final do produto? Veja o código em Java:
// Algoritmo que calcula porcentagem em Java
package estudos;
public class Estudos {
public static void main(String[] args) {
// variáveis usadas na resolução do problema
double valor, percentual, valor_final;
valor = 178.00; // valor original
percentual = 15.0 / 100.0; // 15%
valor_final = valor + (percentual * valor);
// mostra o resultado
System.out.println("O valor final do produto é: " + valor_final);
// O resultado será 204,70
}
}
Ex: 2 - Um produto, cujo valor original era de R$ 250,00, teve um desconto de 8%. Qual foi seu valor final? Veja o código em Java:
// Algoritmo que calcula porcentagem em Java
package estudos;
public class Estudos {
public static void main(String[] args) {
// variáveis usadas na resolução do problema
double valor, percentual, valor_final;
valor = 250.00; // valor original
percentual = 8.0 / 100.0; // 8%
valor_final = valor - (percentual * valor);
// mostra o resultado
System.out.println("O valor final do produto é: " + valor_final);
// O resultado será 230,00
}
}
Ex: 3 - Em um concurso de perguntas e respostas, um jovem acertou 72 das 90 perguntas apresentadas. Qual foi a porcentagem de acertos? E a porcentagem de erros? Veja o código em Java:
// Algoritmo que calcula porcentagem em Java
package estudos;
public class Estudos {
public static void main(String[] args) {
// variáveis usadas na resolução do problema
double perguntas, acertos;
perguntas = 90.0;
acertos = 72.0;
// mostra a porcentagem de acertos
System.out.print("Porcentagem de acertos: ");
System.out.println(((acertos / perguntas) * 100) + "%");
// mostra a porcentagem de erros
System.out.print("Porcentagem de erros: ");
System.out.println((((perguntas - acertos) / perguntas) * 100) + "%");
// Os resultados serão 80% e 20%
}
}
Ex: 4 - Um aparelho de CD foi adquirido por R$ 300,00 e revendido por R$ 340,00. Qual foi a porcentagem de lucro na transação? Veja o código em Java:
// Algoritmo que calcula porcentagem em Java
package estudos;
public class Estudos {
public static void main(String[] args) {
// variáveis usadas na resolução do problema
double valor_anterior, novo_valor, porcentagem_lucro;
valor_anterior = 300.0; // valor anterior
novo_valor = 340.0; // valor novo
// calcula a porcentagem de lucro
// efetua o cálculo
porcentagem_lucro = ((novo_valor * 100) / valor_anterior) - 100;
System.out.println("A porcentagem de lucro foi de: " +
porcentagem_lucro + "%");
// O resultado será 13,33
}
}
Ex: 5 - Uma loja repassa 5% do lucro a seus vendedores. Se um produto custa R$ 70,00, qual o valor em reais repassado a um determinado vendedor? Veja o código em Java:
// Algoritmo que calcula porcentagem em Java
package estudos;
public class Estudos {
public static void main(String[] args) {
// variáveis usadas na resolução do problema
double valor, percentual, comissao;
valor = 70.0; // valor do produto
percentual = 5.0 / 100.0; // 5%
// calcula a comissão
comissao = percentual * valor;
// mostra o resultado
System.out.println("O valor repassado ao vendedor é: " + comissao);
// O resultado será 3,5
}
}
|
C++ ::: Dicas & Truques ::: Strings e Caracteres |
Como embaralhar os caracteres de uma string em C++ usando a função random_shuffle()Quantidade de visualizações: 13086 vezes |
|
Em algumas situações, tais como o desenvolvimento de um gerador de senhas aleatórias, pode ser necessário embaralharmos as letras de uma palavra. Em C++ isso pode ser feito por meio do uso da função random_shuffle() da STL (Standard Template Library). Não se esqueça de efetuar uma chamada a srand() antes do código que embaralha os caracteres da string. Veja o código C++ completo para o exemplo:
#include <string>
#include <iostream>
#include <algorithm>
#include <time.h>
using namespace std;
int main(int argc, char *argv[]){
// vamos iniciar o gerador de números
// aleatórios
srand(time(NULL));
// vamos criar uma string
string palavra = "JAVASCRIPT";
cout << "Palavra original: " << palavra << endl;
// vamos embaralhar as palavras da string
random_shuffle(palavra.begin(), palavra.end());
// exibe o resultado
cout << "Palavra com caracteres embaralhados: " << palavra << "\n\n";
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
Ao executar este código C++ nós teremos o seguinte resultado: Palavra original: JAVASCRIPT Palavra com caracteres embaralhados: RPSAITCVAJ |
Java ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cateto adjascente dadas as medidas da hipotenusa e do cateto oposto em JavaQuantidade de visualizações: 1456 vezes |
|
Nesta dica mostrarei como podemos tirar proveito do Teorema de Pitágoras para obter a medida do cateto adjascente quando temos as medidas da hipotenusa e do cateto oposto. Este teorema diz que "o quadrado da hipotenusa é igual à soma dos quadrados dos catetos", o que torna a nossa tarefa, na linguagem Java, muito fácil. Comece observando a imagem a seguir:  Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. A medida da hipotenusa é, sem arredondamentos, 36.056 metros. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras): \[c^2 = a^2 + b^2\] Tudo que temos que fazer é mudar a fórmula para: \[b^2 = c^2 - a^2\] Veja que agora o quadrado do cateto adjascente é igual ao quadrado da hipotenusa menos o quadrado do cateto oposto. Não se esqueça de que a hipotenusa é o maior lado do triângulo retângulo. Veja agora como esse cálculo é feito em linguagem Java:
package arquivodecodigos;
public class Estudos{
public static void main(String args[]){
double c = 36.056; // medida da hipotenusa
double a = 20; // medida do cateto oposto
// agora vamos calcular a medida da cateto adjascente
double b = Math.sqrt(Math.pow(c, 2) - Math.pow(a, 2));
// e mostramos o resultado
System.out.println("A medida do cateto adjascente é: " +
b);
}
}
Ao executar este código Java nós teremos o seguinte resultado: A medida do cateto adjascente é: 30.00058559428465 Como podemos ver, o resultado retornado com o código Java confere com os valores da imagem apresentada. |
Nossas 20 dicas & truques de programação mais populares |
|
VB.NET - Como adicionar horas à data e hora atual em VB.NET usando a função AddHours() da classe DateTime GoLang - Como retornar o tamanho de uma string em Golang usando os métodos len() e RuneCountInString() |
Você também poderá gostar das dicas e truques de programação abaixo |
|
C# - Como adicionar ou subtrair meses de uma data em C# usando a função AddMonths() da classe DateTime JavaScript - JavaScript Avançado - Como remover todas as ocorrências de uma substring em uma string usando uma função recursiva |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




