 |
|||||
|
|||||
MySQL ::: Dicas & Truques ::: Data e Hora |
Como formatar campos DATE, TIME, DATETIME e TIMESTAMP usando a função DATE_FORMAT() do MySQLQuantidade de visualizações: 25855 vezes |
A função DATE_FORMAT() é usada quando precisamos formatar os valores obtidos de campos do tipo DATE, TIME, DATETIME e TIMESTAMP. Veja um exemplo no qual obtemos o valor de um campo DATE chamado vencimento e o formatamos para o formato 30/10/2007:SELECT DATE_FORMAT(vencimento, '%d/%m/%Y') FROM tabela_estudos A relação de caracteres que podem ser usados na definição do formato para esta função pode ser encontrada em: http://www.arquivodecodigos.com.br/ referencias/mysql/ caracteres_formatacao_data_hora.php |
C ::: Dicas & Truques ::: Ordenação e Pesquisa (Busca) |
C para iniciantes - Como ordenar os elementos de um vetor de inteiros usando a ordenação da bolha (Bubble Sort) na linguagem CQuantidade de visualizações: 9875 vezes |
|
O método ou algorítmo de ordenação da bolha é uma das técnicas mais simples de ordenação. No entanto, este método não é eficiente, visto que o tempo despendido para sua execução é muito elevado se comparado à outros métodos existentes. Geralmente usamos este método quando queremos ordenar 50 elementos ou menos. O entendimento deste método é fácil. Se estivermos ordenandos os valores do menor para o maior, o método da bolha percorre os elementos do vetor (array), comparando e movendo o menor valor para a primeira posição do vetor, tal qual bolhas indo para a superfície. Veja um exemplo completo:
#include <stdio.h>
#include <stdlib.h>
void bubble_sort(int matriz[], int tam){
int temp, i, j;
for(i = 0; i < tam; i++){
for(j = 0; j < tam; j++){
if(matriz[i] < matriz[j]){
temp = matriz[i];
matriz[i] = matriz[j];
matriz[j] = temp;
}
}
}
}
int main(int argc, char *argv[])
{
int valores[] = {4, 6, 2, 8, 1, 9, 3, 0, 11};
int i, tamanho = 9;
// imprime a matriz sem a ordenação
for(i = 0; i < 9; i++){
printf("%d ", valores[i]);
}
// vamos ordenar a matriz
bubble_sort(valores, tamanho);
// imprime a matriz ordenada
puts("\n");
for(i = 0; i < 9; i++){
printf("%d ", valores[i]);
}
puts("\n");
system("pause");
return 0;
}
Ao executar este código nós teremos o seguinte resultado: Sem ordenação: 4, 6, 2, 8, 1, 9, 3, 0, 11 Ordenados: 0, 1, 2, 3, 4, 6, 8, 9, 11 |
Java ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a equação reduzida da reta em Java dados dois pontos pertencentes à retaQuantidade de visualizações: 1390 vezes |
|
Nesta dica de Java veremos como calcular a equação reduzida da reta quando temos dois pontos pertencentes à esta reta. Não, nessa dica não vamos calcular a equação geral da reta, apenas a equação reduzida. Em outras dicas do site você encontra como como isso pode ser feito. Para relembrar: a equação reduzida da reta é y = mx + n, em que x e y são, respectivamente, a variável independente e a variável dependente; m é o coeficiente angular, e n é o coeficiente linear. Além disso, m e n são números reais. Com a equação reduzida da reta, é possível calcular quais são os pontos que pertencem a essa reta e quais não pertencem. Vamos começar então analisando a seguinte figura, na qual temos dois pontos que pertencem à uma reta: 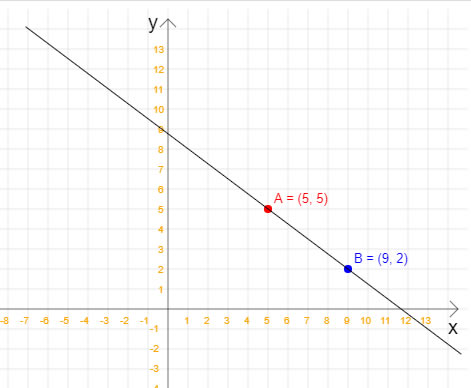 Note que a reta da figura passa pelos pontos A(5, 5) e B(9, 2). Então, uma vez que já temos os dois pontos, já podemos calcular a equação reduzida da reta. Veja o código Java completo para esta tarefa:
package estudos;
import java.util.Scanner;
public class Estudos{
public static void main(String[] args){
// vamos usar a classe Scanner para ler os dados
Scanner entrada = new Scanner(System.in);
// vamos ler as coordenadas do primeiro ponto
System.out.print("Coordenada x do primeiro ponto: ");
double x1 = Double.parseDouble(entrada.nextLine());
System.out.print("Coordenada y do primeiro ponto: ");
double y1 = Double.parseDouble(entrada.nextLine());
// vamos ler as coordenadas do segundo ponto
System.out.print("Coordenada x do segundo ponto: ");
double x2 = Double.parseDouble(entrada.nextLine());
System.out.print("Coordenada y do segundo ponto: ");
double y2 = Double.parseDouble(entrada.nextLine());
String sinal = "+";
// vamos calcular o coeficiente angular da reta
double m = (y2 - y1) / (x2 - x1);
// vamos calcular o coeficiente linear
double n = y1 - (m * x1);
// coeficiente linear menor que zero? O sinal será negativo
if (n < 0){
sinal = "-";
n = n * -1;
}
// mostra a equação reduzida da reta
System.out.println("Equação reduzida: y = " + m + "x"
+ " " + sinal + " " + n);
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 5 Coordenada y do primeiro ponto: 5 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 2 Equação reduzida: y = -0,75x + 8,75 Para testarmos se nossa equação reduzida da reta está realmente correta, considere o valor 3 para o eixo x da imagem acima. Ao efetuarmos o cálculo: >> y = (-0.75 * 3) + 8.75 y = 6.5000 temos o valor 6.5 para o eixo y, o que faz com que o novo ponto caia exatamente em cima da reta considerada na imagem. |
VB.NET ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Como usar o laço Do...While...Loop do VB.NETQuantidade de visualizações: 17704 vezes |
|
Um instrução de repetição (também chamada de laço ou loop) permite que um bloco de códigos seja executado repetidamente até que uma condição seja satisfeita. O laço Do...While...Loop é usado quando queremos testar uma condição e, executar um bloco de código repetidamente enquanto esta condição for verdadeira. Lembre-se de que, se a condição já for falsa, o laço nunca será executado. Veja um exemplo de laço Do...While...Loop que nos permite exibir os números de 0 a 10: Dim numero As Integer = 0 Do While numero <= 10 Console.WriteLine(numero) numero += 1 Loop Veja uma nova versão deste código, desta vez contando de 10 a 0: Dim numero As Integer = 10 Do While numero >= 0 Console.WriteLine(numero) numero -= 1 Loop Aqui nós estamos novamente avaliando uma condição, ou seja, se o resultado da condição for True, a execução do laço continua. Se for False, o laço pára. Veja um exemplo no qual a condição booleana está bem explícita:
Dim pode As Boolean = True
Dim valor As Integer = 1
Do While pode
Console.WriteLine(valor)
valor += 1
If valor > 20 Then
pode = False
End If
Loop
|
C# ::: LINQ ::: LINQ to Objects |
Como retornar o maior elemento em um array de int em C# usando a função Max() do LINQQuantidade de visualizações: 1116 vezes |
|
Nesta dica mostrarei, em um exemplo bem simples, como podemos usar o método Max() do LINQ (Language-Integrated Query) do C# para retornar o maior elemento de um vetor de inteiros. Note que temos um vetor de int com os valores {5, 2, 8, 3, 0, 1} e o valor 8 deverá ser retornado como sendo o maior. Veja o código completo para o exemplo:
using System;
using System.Linq;
namespace Estudos {
class Principal {
static void Main(string[] args) {
// vamos construir um vetor de inteiros
int[] valores = {5, 2, 8, 3, 0, 1};
// vamos obter o maior elemento do vetor
int maior = valores.Max();
// vamos mostrar o resultado
Console.WriteLine("O maior valor é: {0}", maior);
Console.WriteLine("\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: O maior valor é: 8 Fique atento ao fato de que o método Max() pode atirar uma exceção do tipo InvalidOperation se o array ou coleção estiver vazia ou não incluir nenhum elemento que se encaixe nas condições testadas. Veja o resultado ao chamarmos este método em um vetor vazio: System.InvalidOperationException HResult=0x80131509 Message=Sequence contains no elements Source=System.Linq StackTrace: at System.Linq.ThrowHelper.ThrowNoElementsException() at System.Linq.Enumerable.Max(IEnumerable`1 source) at Estudos.Principal.Main(String[] args) in C:\estudos_c#\Estudos\Principal.cs:line 11 |
JavaScript ::: Dicas & Truques ::: Matemática e Estatística |
JavaScript para matemática - Como obter o menor entre dois ou mais valores numéricos usando a função min() do JavaScriptQuantidade de visualizações: 7859 vezes |
|
A função min() do objeto Math da linguagem JavaScript pode ser usada quando temos dois ou mais valores numéricos e gostaríamos de retornar o menor deles. Note que esta função não aceita um vetor (array) como argumento, ou seja, os valores devem ser fornecidos de forma literal ou passados como variáveis independentes. Veja o código JavaScript completo para o exemplo:
<html>
<head>
<title>Estudando JavaScript</title>
</head>
<body>
<script type="text/javascript">
var n1 = 45;
var n2 = 18;
var menor = Math.min(n1, n2);
document.write("O menor número é " + menor);
</script>
</body>
</html>
Ao executar este código nós teremos o seguinte resultado: O menor número é 18 O retorno do método min() é um objeto Number representando o menor dos valores fornecidos. Se nenhum argumento for informado, o retorno será um objeto Infinity, enquanto um objeto NaN será retornado se algum dos valores fornecidos não for um valor numérico válido. |
VisuAlg ::: Desafios e Lista de Exercícios Resolvidos ::: VisuAlg Básico |
Exercícios Resolvidos de VisuAlg - Escreva um programa VisuAlg para calcular e imprimir o número de lâmpadas necessáriasQuantidade de visualizações: 366 vezes |
|
Pergunta/Tarefa: Escreva um programa VisuAlg para calcular e imprimir o número de lâmpadas necessárias para iluminar um determinado cômodo de uma residência. Dados de entrada: a potência da lâmpada utilizada (em watts), as dimensões (largura e comprimento, em metros) do cômodo. Considere que a potência necessária é de 18 watts por metro quadrado. Sua saída deverá ser parecida com: Informe a potência da lâmpada (em watts): 100 Informe a largura do cômodo (em metros): 6 Informe o comprimento do cômodo (em metros): 4 Serão necessárias 4 lâmpadas. Veja a resolução completa para o exercício em VisuAlg, comentada linha a linha:
algoritmo "Como calcular o número de lâmpadas necessárias"
var
// variáveis usadas na resolução do problema
potencia_lampada, largura_comodo, comprimento_comodo: real
area_comodo, potencia_total: real
quant_lampadas: inteiro
inicio
// vamos ler a potência da lâmpada
escreva("Informe a potência da lâmpada (em watts): ")
leia(potencia_lampada)
// vamos ler a largura do cômodo
escreva("Informe a largura do cômodo (em metros): ")
leia(largura_comodo)
// agora vamos ler o comprimento do cômodo
escreva("Informe o comprimento do cômodo (em metros): ")
leia(comprimento_comodo)
// agora vamos calcular a área do cômodo
area_comodo <- largura_comodo * comprimento_comodo
// calculamos a potência total necessária para iluminar
// todo o cômodo
potencia_total <- area_comodo * 18
// e finalmente calculamos a quantidade de lâmpadas necessárias
quant_lampadas <- Int(potencia_total / potencia_lampada)
// será necessário no mínimo uma lâmpada
se quant_lampadas = 0 entao
quant_lampadas <- quant_lampadas + 1
fimse
// e mostramos o resultado
escreva("Serão necessárias ", quant_lampadas, " lâmpadas.")
fimalgoritmo
|
Python ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em Python dados dois pontos no plano cartesianoQuantidade de visualizações: 3215 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem Python que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
# vamos importar o módulo Math
import math as math
def main():
# x e y do primeiro ponto
x1 = float(input("Coordenada x do primeiro ponto: "))
y1 = float(input("Coordenada y do primeiro ponto: "))
# x e y do segundo ponto
x2 = float(input("Coordenada x do segundo ponto: "))
y2 = float(input("Coordenada y do segundo ponto: "))
# agora vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1)
# e mostramos o resultado
print("O coeficiente angular é: %f\n\n" % m)
if __name__== "__main__":
main()
Ao executar este código em linguagem Python nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.666667 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
# vamos importar o módulo Math
import math as math
def main():
# x e y do primeiro ponto
x1 = float(input("Coordenada x do primeiro ponto: "))
y1 = float(input("Coordenada y do primeiro ponto: "))
# x e y do segundo ponto
x2 = float(input("Coordenada x do segundo ponto: "))
y2 = float(input("Coordenada y do segundo ponto: "))
# vamos obter o comprimento do cateto oposto
cateto_oposto = y2 - y1
# e agora o cateto adjascente
cateto_adjascente = x2 - x1
# vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
# (em radianos, não se esqueça)
tetha = math.atan2(cateto_oposto, cateto_adjascente)
# e finalmente usamos a tangente desse ângulo para calcular
# o coeficiente angular
tangente = math.tan(tetha)
# e mostramos o resultado
print("O coeficiente angular é: %f\n\n" % tangente)
if __name__== "__main__":
main()
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Node.js ::: Express.js ::: Passos Iniciais |
Node.js Express.js - Como escrever sua primeira aplicação Express.jsQuantidade de visualizações: 2195 vezes |
|
Se você chegou até esta página vindo(a) de um sistema de busca tal como o Google, saiba que o Express.js é um framework web baseado no núcleo do Node.js, ou seja, antes de experimentar o exemplo abaixo, você deve ter uma instalação funcional do Node.js na sua máquina. Além disso, o módulo express deve estar instalado também, e 100% operacional. No entanto, se sua instalação do Node.js ainda não tem o express, basta entrar no diretório que você instalou o Node.js e disparar o comando a seguir: npm install express Verifique se a instalação foi feita com sucesso e vamos continuar. Este exemplo é bem simples e requer apenas um arquivo. Para tanto, abra o seu editor de código favorito e digite a listagem abaixo:
// vamos importar o módulo express
var express = require('express');
// o servidor vai ouvir na porta 8081
var porta = 8081;
var app = express();
// o asterisco (*) quer dizer que todas as requisições vão cair aqui
app.get('*', function(request, response){
response.end('Tamo juntos!');
});
app.listen(porta, function(){
console.log('O servidor está ouvindo em http://localhost:%s', porta);
});
Salve o arquivo como servidor.js e execute o Node.js. Em seguida abra o seu navegador web no endereço http://localhost:8081 e veja o resultado. Agora não deixe de ver nossas outras dicas de Node.js e aprender cada vez mais. |
PHP ::: Dicas & Truques ::: URLs, Documentos e Páginas |
PHP para iniciantes - Como obter uma lista completa das variáveis de ambiente disponíveis no servidorQuantidade de visualizações: 10391 vezes |
|
Nesta dica mostrarei como é possível combinar o vetor de variáveis de ambiente $_SERVER e o laço foreach() da linguagem PHP para obter uma lista completa das variáveis de ambiente disponíveis no servidor web a partir do qual nossos códigos PHP estão sendo executados. Esta técnica é excelente para depuração (debugging) de código PHP. Veja o código PHP completo para o exemplo:
<html>
<head>
<title>Estudando PHP</title>
</head>
<body>
<?php
foreach($_SERVER as $env => $valor){
echo $env . " = " . $valor . "<br>";
}
?>
</body>
</html>
Ao executar este código PHP nós teremos um resultado parecido com: SERVER_SOFTWARE = Apache/2.4.46 (Win64) OpenSSL/1.1.1h PHP/8.0.0 SERVER_NAME = localhost SERVER_ADDR = ::1 SERVER_PORT = 80 REMOTE_ADDR = ::1 DOCUMENT_ROOT = C:/xampp/htdocs REQUEST_SCHEME = http CONTEXT_PREFIX = CONTEXT_DOCUMENT_ROOT = C:/xampp/htdocs SERVER_ADMIN = postmaster@localhost SCRIPT_FILENAME = C:/xampp/htdocs/estudos/index.php REMOTE_PORT = 61618 GATEWAY_INTERFACE = CGI/1.1 SERVER_PROTOCOL = HTTP/1.1 REQUEST_METHOD = GET QUERY_STRING = REQUEST_URI = /estudos/index.php SCRIPT_NAME = /estudos/index.php PHP_SELF = /estudos/index.php REQUEST_TIME_FLOAT = 1618495343.0591 REQUEST_TIME = 1618495343 |
Nossas 20 dicas & truques de programação mais populares |
|
Java - Exercícios Resolvidos de Java - Como calcular e exibir os 50 primeiros números primos em Java QGIS - Como retornar o título do projeto do QGIS usando PyQGIS e a função title() da classe QgsProject |
Você também poderá gostar das dicas e truques de programação abaixo |
|
AutoCAD Civil 3D .NET C# - Como pedir para o usuário selecionar um alinhamento no Civil 3D usando a função GetEntity() do AutoCAD Civil 3D .NET C# API jQuery - jQuery para iniciantes - Como obter o conteúdo de um elemento HTML usando a função html() do jQuery Java Servlets - Como compartilhar dados entre um Java Servlet e uma página JSP usando a requisição HttpServletRequest |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





