Java ::: Desafios e Lista de Exercícios Resolvidos ::: Java Básico |
Exercícios Resolvidos de Java - Ler um número de três dígitos, separá-lo e invertê-lo, escrevendo o número lido e sua forma inversaQuantidade de visualizações: 16063 vezes |
|
Exercício Resolvido de Java - Ler um número de três dígitos, separá-lo e invertê-lo, escrevendo o número lido e sua forma inversa Pergunta/Tarefa: Escreva um programa Java console ou GUI que leia um número de 3 dígitos e o inverta, escrevendo o número lido e o invertido. Por exemplo, se o usuário informar o valor 753, seu programa deverá invertê-lo, resultando em 357. Seu programa deverá exibir a seguinte saída: Informe um valor inteiro de três dígitos: 753 O valor original é: 753 O valor invertido é: 357 Veja a resolução comentada deste exercício usando Java console:
public static void main(String[] args){
// não se esqueça de adicionar um import para a classe Scanner
// import java.util.Scanner;
// vamos criar um objeto da classe Scanner
Scanner entrada = new Scanner(System.in);
// vamos solicitar ao usuário que informe um valor inteiro
// na faixa 100 a 999 (incluindo)
System.out.print("Informe um valor inteiro de três dígitos: ");
// vamos ler o valor informado
int valor = Integer.parseInt(entrada.next());
// vamos verificar se o valor está na faixa permitida
if(valor < 100 || valor > 999){
System.out.println("Valor fora da faixa permitida");
System.exit(0);
}
// vamos criar uma variável temporária para manter intacto o valor lido
int temp = valor;
int inverso = 0; // guardará o valor invertido
// vamos inverter o valor agora
while(temp != 0){
inverso = (inverso * 10) + (temp % 10);
temp = temp / 10;
}
// vamos mostrar o resultado
System.out.println("O valor original é: " + valor);
System.out.println("O valor invertido é: " + inverso);
}
|
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Programação Orientada a Objetos |
Exercício Resolvido de Python - Uma classe para representar uma pessoa, com os atributos privados de nome, data de nascimento e alturaQuantidade de visualizações: 9703 vezes |
|
Pergunta/Tarefa: Crie uma classe para representar uma pessoa, com os atributos privados de nome, data de nascimento e altura. Crie os métodos públicos necessários para sets e gets e também um método para imprimir todos dados de uma pessoa. Crie um método para calcular a idade da pessoa. A data de nascimento pode ser informada como uma String (no formato 05/10/1982, por exemplo) e, no cálculo da idade, considere apenas o ano da data de nascimento informada. Sua saída deverá ser parecida com: 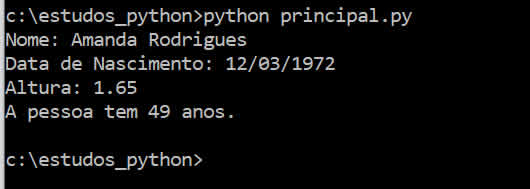 Resposta/Solução: Veja a resolução comentada deste exercício usando Python console: Código para a classe Pessoa (pessoa.py):
from datetime import datetime
class Pessoa:
# construtor da classe Pessoa
def __init__(self, nome, data_nascimento, altura):
self._nome = nome
self._data_nascimento = data_nascimento
self._altura = altura
# método que imprime todos os dados da pessoa
def imprimir_dados(self):
print("Nome:", self._nome, "\nData de Nascimento:" ,
self._data_nascimento, "\nAltura:", self._altura)
# método que calcula a idade da pessoa
def calcular_idade(self):
# vamos obter o ano da data de hoje
ano_data_atual = datetime.today().year
# agora vamos obter o ano de nascimento da pessoa
partes_data_nascimento = self._data_nascimento.split("/")
ano_nascimento = partes_data_nascimento[2]
# agora mostramos a idade da pessoa
anos = ano_data_atual - int(ano_nascimento)
print("A pessoa tem", anos, "anos.")
# método que define o nome da pessoa
def set_nome(self, nome):
self._nome = nome
# método que obtém o nome da pessoa
def get_nome(self):
return self._nome
# método que define a data de nascimento da pessoa
def set_data_nascimento(self, data_nascimento):
self._data_nascimento = data_nascimento
# método que obtém a data de nascimento da pessoa
def get_data_nascimento(self):
return self._data_nascimento
# método que define a altura da pessoa
def set_altura(self, altura):
self._data_altura = altura
# método que obtém a altura da pessoa
def get_altura(self):
return self._altura
Código para o arquivo principal.py:
# importa a classe Pessoa
from pessoa import Pessoa
def main():
# cria um novo objeto da classe Pessoa
pessoa = Pessoa("Amanda Rodrigues", "12/03/1972", 1.65)
# exibe os dados da pessoa
pessoa.imprimir_dados()
# mostra a idade da pessoa
pessoa.calcular_idade()
if __name__== "__main__":
main()
|
PHP ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como converter graus em radianos em PHP usando a função deg2rad() - Trigonometria para iniciantesQuantidade de visualizações: 14542 vezes |
|
As unidades grau e radiano são muito usadas em cálculos de trigonometria. O grau é de uso mais no cotidiano pela sua praticidade, pois envolve, na maioria dos casos, números inteiros. O radiano é de uso em cálculos envolvendo geralmente números racionais (e também na programação gráfica, uma vez que praticamente todas as linguagens de programação possuem funções de trigonometria que requerem e retornam valores em radianos, e não em graus). Graus podem ser convertidos para radianos usando-se a seguinte fórmula:  Note que o valor de PI é 3,14 (aproximadamente). Veja agora um trecho de código PHP que converte um ângulo em graus para radianos: <html> <head> <title>Estudando PHP</title> </head> <body> <?php $graus = 45; $radianos = ($graus / 180) * pi(); echo "Ângulo em graus: " . $graus . "<br>"; echo "Ângulo em radianos: " . $radianos; ?> </body> </html> Ao executarmos este código nós teremos o seguinte resultado: Ângulo em graus: 45 Ângulo em radianos: 0.78539816339745 O PHP, na contramão de várias outras linguagens de programação, nos fornece uma função já embutida que nos permite converter de graus para radianos. Esta função se chama deg2rad(), recebe um valor em graus e devolve o resultado em radianos. Veja como usá-la no código PHP abaixo: <html> <head> <title>Estudando PHP</title> </head> <body> <?php $graus = 45; $radianos = deg2rad($graus); echo "Ângulo em graus: " . $graus . "<br>"; echo "Ângulo em radianos: " . $radianos; ?> </body> </html> Ao executarmos o código novamente, teremos o seguinte resultado: Ângulo em graus: 45 Ângulo em radianos: 0.78539816339745 Veja que o resultado obtido com o uso da função deg2rad() foi o mesmo que obtivemos com o cálculo no início da dica. Para finalizar, saiba que 45o, assim como 30o e 60o são conhecidos como ângulos notáveis, e seus valores em radianos, assim como seus seno, cosseno e tangentes, devem ser memorizados se você quiser se tornar um guru (ou guroa) em geometria e trigonometria (e em computação gráfica, é claro). |
PHP ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como embaralhar os elementos de um array em PHP usando a função shuffle() - Vetores e matrizes em PHPQuantidade de visualizações: 12759 vezes |
|
Em algumas situações nós precisamos misturar os elementos de um vetor em PHP, ou seja, embaralhar de forma aleatória os elementos. Para isso nós podemos usar a função shuffle(), que recebe um vetor e o devolve com a ordem dos elementos embaralhada de forma randômica. Veja o exemplo completo:
<html>
<head>
<title>Estudando PHP</title>
</head>
<body>
<?php
$nomes = array("Osmar", "Marcos", "Igor", "Gustavo");
// ordem original
for($i = 0; $i < count($nomes); $i++){
echo $nomes[$i] . "<br>";
}
echo "<br>";
// embaralha o vetor
shuffle($nomes);
// ordem embaralhada
for($i = 0; $i < count($nomes); $i++){
echo $nomes[$i] . "<br>";
}
?>
</body>
</html>
Ao executar este código nós teremos o seguinte resultado: Osmar Marcos Igor Gustavo Gustavo Osmar Marcos Igor |
JavaScript ::: Dicas & Truques ::: Mouse e Teclado |
Como bloquear o botão direito do mouse em suas páginas HTML usando JavaScriptQuantidade de visualizações: 90 vezes |
|
Em algumas situações, principalmente games desenvolvidos em JavaScript ou HTML5, nós gostaríamos de evitar o botão direito do mouse, ou seja, o menu de contexto no corpo da página web. Para isso só precisamos retornar false para o evento oncontextmenu. Veja como isso pode ser feito no trecho de código JavaScript abaixo: <html> <head> <title>Estudos JavaScript</title> </head> <body oncontextmenu="return false"> <h1>Você não pode usar o botão direito nessa página</h1> </body> </html> Uma boa idéia é avisar ao usuário (por meio de uma mensagem window.alert) que ele não pode usar o botão de contexto no documento HTML. Veja:
<html>
<head>
<title>Estudos JavaScript</title>
</head>
<body oncontextmenu="return aviso()">
<script type="text/javascript">
function aviso(){
window.alert("Botão direito não permitido.");
return false;
}
</script>
</body>
</html>
Agora, ao clicarmos com o botão direito do mouse na página, uma mensagem window.alert será exibida com o seguinte texto: Botão direito não permitido. |
GNU Octave ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em GNU Octave dados dois pontos no plano cartesianoQuantidade de visualizações: 1552 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem GNU Octave (script GNU Octave) que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
# x e y do primeiro ponto
x1 = input("Coordenada x do primeiro ponto: ")
y1 = input("Coordenada y do primeiro ponto: ")
# x e y do segundo ponto
x2 = input("Coordenada x do segundo ponto: ")
y2 = input("Coordenada y do segundo ponto: ")
# agora vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1)
# mostramos o resultado
fprintf("O coeficiente angular é: %f\n\n", m)
Ao executar este código em linguagem GNU Octave nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 x1 = 3 Coordenada y do primeiro ponto: 6 y1 = 6 Coordenada x do segundo ponto: 9 x2 = 9 Coordenada y do segundo ponto: 10 y2 = 10 m = 0.6667 O coeficiente angular é: 0.666667 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
# x e y do primeiro ponto
x1 = input("Coordenada x do primeiro ponto: ")
y1 = input("Coordenada y do primeiro ponto: ")
# x e y do segundo ponto
x2 = input("Coordenada x do segundo ponto: ")
y2 = input("Coordenada y do segundo ponto: ")
# vamos obter o comprimento do cateto oposto
cateto_oposto = y2 - y1
# e agora o cateto adjascente
cateto_adjascente = x2 - x1
# vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
# (em radianos, não se esqueça)
tetha = atan2(cateto_oposto, cateto_adjascente)
# e finalmente usamos a tangente desse ângulo para calcular
# o coeficiente angular
tangente = tan(tetha)
# mostramos o resultado
fprintf("O coeficiente angular é: %f\n\n", tangente)
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
C ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em C usando a função cos() do header math.h - Calculadora de cosseno em CQuantidade de visualizações: 11183 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da linguagem C. Esta função, que faz parte do header math.h, recebe um valor numérico double e retorna um valor double, ou seja, também numérico) entre -1 até 1 (ambos inclusos). Veja:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(int argc, char *argv[]){
// vamos calcular o cosseno de três números
printf("Cosseno de 0 = %f\n", cos(0));
printf("Cosseno de 1 = %f\n", cos(1));
printf("Cosseno de 2 = %f\n", cos(2));
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: Cosseno de 0 = 1.000000 Cosseno de 1 = 0.540302 Cosseno de 2 = -0.416147 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 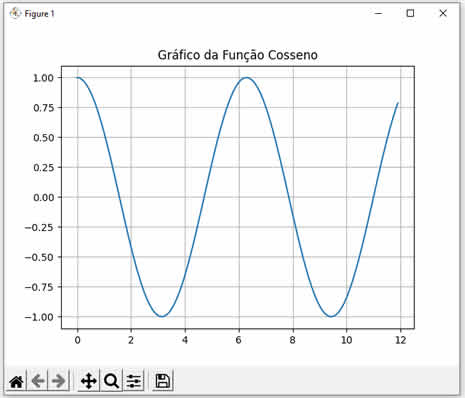 |
Java ::: Classes e Componentes ::: JTextArea |
Java Swing - Como salvar o conteúdo de um JTextArea em um arquivo (usando um JFileChooser para localizar o diretório e arquivo)Quantidade de visualizações: 201 vezes |
|
Nesta dica mostrarei como é possível como salvar o conteúdo de um JTextArea em um arquivo texto. Essa operação é muito frequente em aplicações Java Swing. Note que faremos uso de um JFileChooser para localizar o arquivo no qual o conteúdo será gravado, ou poderemos informar o nome do arquivo. Observe também o uso do método write() da classe FileWriter para escrever o conteúdo no arquivo. Para finalizar, perceba que não fiz os devidos tratamentos de erros e as mensagens de sucesso das operações e coisas. Fica como exercício para você finalizar. Veja o código completo:
package arquivodecodigos;
import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
import java.io.*;
public class Estudos extends JFrame{
JTextArea textArea;
JButton btn;
public Estudos() {
super("Salvando o conteúdo de um JTextArea em um arquivo");
Container c = getContentPane();
FlowLayout layout = new FlowLayout(FlowLayout.LEFT);
c.setLayout(layout);
textArea = new JTextArea(10, 20);
textArea.setLineWrap(true);
btn = new JButton("Salvar Arquivo");
btn.addActionListener(
new ActionListener(){
public void actionPerformed(ActionEvent e){
JFileChooser fc = new JFileChooser();
if(fc.showSaveDialog(Estudos.this) != JFileChooser.APPROVE_OPTION){
return;
}
File arquivo = fc.getSelectedFile();
if(arquivo == null){
return;
}
FileWriter writer = null;
try {
writer = new FileWriter(arquivo);
writer.write(textArea.getText());
}
catch(IOException ex){
// Possiveis erros aqui
}
finally {
if(writer != null){
try{
writer.close();
}
catch (IOException x){
// trate os erros aqui
}
}
}
}
}
);
c.add(textArea);
c.add(btn);
setSize(350, 250);
setVisible(true);
}
public static void main(String args[]){
Estudos app = new Estudos();
app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
}
|
Java ::: Dicas & Truques ::: Ordenação e Pesquisa (Busca) |
Como implementar a ordenação Quicksort em Java - Apostila de Java para iniciantesQuantidade de visualizações: 438 vezes |
|
A ordenação Quicksort é um dos algorítmos de ordenação mais encontrados em aplicações reais de programação. No Delphi esta ordenação é encontrada no objeto TList. No Java podemos encontrá-lo no método Arrays.sort(). Na linguagem C a ordenação Quicksort é implementada na função qsort() da biblioteca padrão. O algoritmo de ordenação Quicksort é do tipo dividir para conquistar (divide-and-conquer principle). Neste tipo de algoritmo o problema é dividido em sub-problemas e a solução é concatenada quando as chamadas recursivas atingirem o caso base. O vetor (ou array) a ser ordenado é dividido em duas sub-listas por um elemento chamado pivô, resultando em uma lista com elementos menores que o pivô e outra lista com os elementos maiores que o pivô. Esse processo é repetido para cada chamada recursiva. Sim, a ordenação Quicksort faz uso extensivo de recursividade, razão pela qual devemos ter muito cuidado para não estourar a pilha do sistema. Existem muitos estudos sobre o pivô ideal para a ordenação Quicksort. Nessa dica adotarei o último elemento do array ou sub-array como pivô. Em vetores não ordenados essa estratégia, em geral, resulta em uma boa escolha. Vamos ao código Java então? Veja um programa Java completo demonstrando o uso da ordenação Quicksort para um array de 10 elementos inteiros:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
// vamos declarar um array de 10 elementos
int valores[] = new int[10];
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// vamos pedir ao usuário para informar os valores para o vetor
for(int i = 0; i < valores.length; i++){
System.out.print("Informe o valor do elemento " + i + ": ");
valores[i] = Integer.parseInt(entrada.nextLine());
}
// vamos mostrar o array informado
System.out.println("\nO array informado foi:\n");
for(int i = 0; i < valores.length; i++){
System.out.print(valores[i] + " ");
}
// vamos ordenar o vetor usando a ordenação Quicksort
quickSort(valores, 0, valores.length - 1);
System.out.println("\n\nO array ordenado é:\n");
for(int i = 0; i < valores.length; i++){
System.out.print(valores[i] + " ");
}
System.out.println("\n\n");
}
// função de implementação da ordenação Quicksort
public static void quickSort(int vetor[], int inicio, int fim) {
// o início é menor que o fim?
if (inicio < fim) {
// vamos obter o novo índice da partição
int indiceParticao = particionar(vetor, inicio, fim);
// efetuamos novas chamadas recursivas
quickSort(vetor, inicio, indiceParticao - 1);
quickSort(vetor, indiceParticao + 1, fim);
}
}
// função que retorna o índice de partição
private static int particionar(int vetor[], int inicio, int fim) {
// para guardar o pivô
int pivot = vetor[fim];
int i = (inicio - 1);
for (int j = inicio; j < fim; j++) {
if (vetor[j] <= pivot) {
i++;
// fazemos a troca
int temp = vetor[i];
vetor[i] = vetor[j];
vetor[j] = temp;
}
}
// efetua a troca
int temp = vetor[i + 1];
vetor[i + 1] = vetor[fim];
vetor[fim] = temp;
return i + 1;
}
}
Ao executar este código Java nós teremos o seguinte resultado: Informe o valor do elemento 0: 7 Informe o valor do elemento 1: 2 Informe o valor do elemento 2: 43 Informe o valor do elemento 3: 1 Informe o valor do elemento 4: 9 Informe o valor do elemento 5: 6 Informe o valor do elemento 6: 22 Informe o valor do elemento 7: 3 Informe o valor do elemento 8: 37 Informe o valor do elemento 9: 5 O array informado foi: 7 2 43 1 9 6 22 3 37 5 O array ordenado é: 1 2 3 5 6 7 9 22 37 43 |
Flutter ::: Material Library - Biblioteca Material ::: TextField |
Como habilitar ou desabilitar um botão ao digitar em um widget TextField do FlutterQuantidade de visualizações: 3774 vezes |
|
Nesta dica eu mostro como podemos habilitar ou desabilitar um botão ElevatedButton dependendo do conteúdo de um TextField. Para isso nós vamos usar a propriedade onChanged da classe TextField para desabilitar o botão quando a caixa de texto estiver vazia e habilitá-lo em caso contrário. O truque aqui é passar um valor null para a propriedade onPressed do ElevatedButton. Só isso já basta para que o botão fique desabilitado. Veja o código completo para o exemplo:
import 'package:flutter/material.dart';
// método principal do Dart, que inicia a aplicação
void main() {
runApp(MeuApp());
}
class MeuApp extends StatelessWidget {
// Este widget é a raiz da aplicação Flutter
@override
Widget build(BuildContext context) {
return MaterialApp(
title: 'Controle TextField',
theme: ThemeData(
primarySwatch: Colors.blue,
),
home: TelaInicial(),
);
}
}
// Vamos construir a view e retornar para a raiz da aplicação
class TelaInicial extends StatefulWidget {
TelaInicial({Key key}) : super(key: key);
@override
_TelaInicialState createState() => _TelaInicialState();
}
class _TelaInicialState extends State<TelaInicial> {
bool btnDesabilitado = true; // vamos desabilitar o botão
@override
Widget build(BuildContext context) {
// vamos criar uma caixa de texto chamada nomeTxt
final nomeTxt = TextField(
decoration: InputDecoration(
border: OutlineInputBorder(
borderRadius: BorderRadius.circular(10.0)),
hintText: 'Digite seu nome'
),
// Vamos detectar a mudança de conteúdo do TextField
onChanged: (String value) async {
// setState() força a atualização da janela
if(value.isEmpty) { // o campo de texto não está vazio
setState(() {
btnDesabilitado = true; // desabilita o botão
});
}
else{
setState(() {
btnDesabilitado = false; // habilita o botão
});
}
}
);
final btnNome = ElevatedButton(
onPressed: btnDesabilitado ? null : (){},
child: Text('Clique Aqui'),
);
return Scaffold(
appBar: AppBar(
title: Text("O Widget TextField"),
),
body: Center(
child: Container(
child: Padding(
padding: const EdgeInsets.all(20.0),
child: Column(
children: <Widget>[
// a caixa de texto TextField vai aqui
nomeTxt,
// o botão vai aqui
btnNome,
],
),
),
),
),
);
}
}
|
Nossas 20 dicas & truques de programação mais populares |
|
C# - Como converter um tipo string para um tipo decimal em C# usando o método Parse() da classe Decimal Java - Como inserir uma substring em uma string em Java usando o método insert() da classe StringBuffer |
Você também poderá gostar das dicas e truques de programação abaixo |
|
GoLang - Como retornar o tamanho de uma string em Golang usando os métodos len() e RuneCountInString() |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





