PHP ::: Dicas & Truques ::: Variáveis e Constantes |
Como testar se uma variável é do tipo float (número de ponto-flutuante) usando as funções is_float() e is_real() do PHPQuantidade de visualizações: 12777 vezes |
|
Em algumas situações podemos querer saber se o tipo de uma variável é float, ou seja, contém um valor com casas decimais. Este teste pode ser feito com o auxílio da função is_float() ou is_real(). Esta função retorna um valor true ou false dependendendo do tipo de variável sendo testada.
<?php
$valor = 0.6;
if(is_float($valor)){
echo 'A variável $valor é do tipo float';
}
?>
Ao executar este código PHP nós teremos o seguinte resultado: A variável $valor é do tipo float |
Java ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em Java usando o método cos() da classe Math - Calculadora de cosseno em JavaQuantidade de visualizações: 1728 vezes |
|
Como calcular o cosseno de um ângulo em Java usando o método cos() da classe Math - Calculadora de cosseno em Java Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da linguagem Java. Esta método, que faz parte da classe Math, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja:
package arquivodecodigos;
public class Estudos{
public static void main(String args[]){
System.out.println("Cosseno de 0 = " + Math.cos(0));
System.out.println("Cosseno de 1 = " + Math.cos(1));
System.out.println("Cosseno de 2 = " + Math.cos(2));
}
}
Ao executar este código Java nós teremos o seguinte resultado: Cosseno de 0 = 1.0 Cosseno de 1 = 0.5403023058681398 Cosseno de 2 = -0.4161468365471424 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 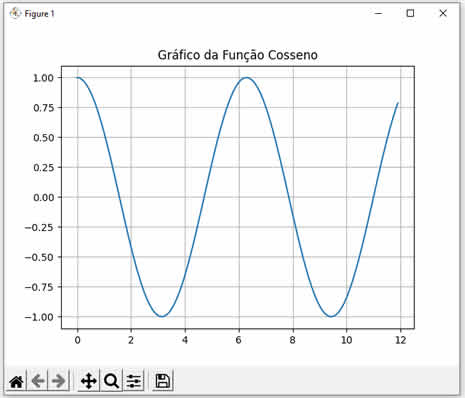 |
HTML5 ::: HTML5 + JavaScript ::: Canvas |
Como carregar uma imagem (ou foto) no objeto Canvas do HTML5Quantidade de visualizações: 2463 vezes |
O objeto Canvas do HTML5 nos permite carregar uma imagem ou foto em tempo de execução e desenhá-la em sua superfície. Para isso, comece criando um objeto Image para guardar a imagem temporariamente na memória:var imagem = new Image(); // vamos carregar a logo do nosso site imagem.src = "https://www.arquivodecodigos.com.br/logo.jpg"; O passo seguinte é adicionar um "ouvidor" de evento neste objeto Image para que ele nos avise quando a imagem estiver 100% carregada. Veja:
// vamos adicionar um "ouvidor" de evento no objeto Image
imagem.addEventListener('load', desenharImagem);
Pronto! Veja que agora, quando o evento load do objeto Image disparar, a função desenharImagem será chamada e a imagem será então desenhada no Canvas. Veja:
function desenharImagem(){
// obtemos uma referência ao elemento Canvas
var canvas = document.getElementById("canvas1");
// obtemos o contexto de desenho
var contexto = canvas.getContext("2d");
// e finalmente desenhamos a imagem
contexto.drawImage(imagem, 0, 0);
}
E aqui está o código completo para o exemplo:
<html>
<head>
<title>O objeto Canvas do HTML5</title>
</head>
<body>
<Canvas id="canvas1" width="500" height="350"></Canvas>
<script type="text/javascript">
var imagem = new Image();
// vamos carregar a logo do nosso site
imagem.src = "https://www.arquivodecodigos.com.br/logo.jpg";
// vamos adicionar um "ouvidor" de evento no objeto Image
imagem.addEventListener('load', desenharImagem);
function desenharImagem(){
// obtemos uma referência ao elemento Canvas
var canvas = document.getElementById("canvas1");
// obtemos o contexto de desenho
var contexto = canvas.getContext("2d");
// e finalmente desenhamos a imagem
contexto.drawImage(imagem, 0, 0);
}
</script>
</body>
</html>
Ao executar a página nós teremos o seguinte resultado:  |
Delphi ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em Delphi dados dois pontos no plano cartesianoQuantidade de visualizações: 1394 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem Delphi que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
procedure TForm4.Button2Click(Sender: TObject);
var
x1, y1, x2, y2, m: Double;
begin
// x e y do primeiro ponto
x1 := 3;
y1 := 6;
// x e y do segundo ponto
x2 := 9;
y2 := 10;
// agora vamos calcular o coeficiente angular
m := (y2 - y1) / (x2 - x1);
// e mostramos o resultado
Memo1.Lines.Add('O coeficiente angular é: ' +
FloatToStr(m));
end;
Ao executar este código em linguagem Delphi nós teremos o seguinte resultado: O coeficiente angular é: 0,666666666666667 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
procedure TForm4.Button2Click(Sender: TObject);
var
x1, y1, x2, y2, tangente: Double;
cateto_oposto, cateto_adjascente, tetha: Double;
begin
// incluir a unit Math
// x e y do primeiro ponto
x1 := 3;
y1 := 6;
// x e y do segundo ponto
x2 := 9;
y2 := 10;
// vamos obter o comprimento do cateto oposto
cateto_oposto := y2 - y1;
// e agora o cateto adjascente
cateto_adjascente := x2 - x1;
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
tetha := ArcTan2(cateto_oposto, cateto_adjascente);
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
tangente := Tan(tetha);
// e mostramos o resultado
Memo1.Lines.Add('O coeficiente angular é: ' +
FloatToStr(tangente));
end;
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
JavaScript ::: Dicas & Truques ::: Matemática e Estatística |
Como resolver uma equação do segundo grau em JavaScript - Como calcular Bhaskara em JavaScriptQuantidade de visualizações: 938 vezes |
|
Como resolver uma equação do 2º grau usando JavaScript Nesta dica mostrarei como encontrar as raízes de uma equação quadrática, ou seja, uma equação do 2º usando a linguagem JavaScript. Definimos como equação do 2º grau ou equações quadráticas qualquer equação do tipo ax² + bx + c = 0 em que a, b e c são números reais e a ≠ 0. Ela recebe esse nome porque, no primeiro membro da igualdade, há um polinômio de grau dois com uma única incógnita. Note que, dos coeficientes a, b e c, somente o a é diferente de zero, pois, caso ele fosse igual a zero, o termo ax² seria igual a zero, logo a equação se tornaria uma equação do primeiro grau: bx + c = 0. Independentemente da ordem da equação, o coeficiente a sempre acompanha o termo x², o coeficiente b sempre acompanha o termo x, e o coeficiente c é sempre o termo independente. Como resolver uma equação do 2º grau Conhecemos como soluções ou raízes da equação ax² + bx + c = 0 os valores de x que fazem com que essa equação seja verdadeira. Uma equação do 2º grau pode ter no máximo dois números reais que sejam raízes dela. Para resolver equações do 2º grau completas, existem dois métodos mais comuns: a) Fórmula de Bhaskara; b) Soma e produto. O primeiro método é bastante mecânico, o que faz com que muitos o prefiram. Já para utilizar o segundo, é necessário o conhecimento de múltiplos e divisores. Além disso, quando as soluções da equação são números quebrados, soma e produto não é uma alternativa boa. Como resolver uma equação do 2º grau usando Bhaskara Como nosso código JavaScript vai resolver a equação quadrática usando a Fórmula de Bhaskara, o primeiro passo é encontrar o determinante. Veja: \[\Delta =b^2-4ac\] Nem sempre a equação possui solução real. O valor do determinante é que nos indica isso, existindo três possibilidades: a) Se determinante > 0, então a equação possui duas soluções reais. b) Se determinante = 0, então a equação possui uma única solução real. c) Se determinante < 0, então a equação não possui solução real. Encontrado o determinante, só precisamos substituir os valores, incluindo o determinante, na Fórmula de Bhaskara: \[x = \dfrac{- b\pm\sqrt{b^2- 4ac}}{2a}\] Vamos agora ao código JavaScript. Nossa aplicação vai pedir para o usuário informar os valores dos três coeficientes a, b e c e, em seguida, vai apresentar as raizes da equação:
<!doctype html>
<html>
<head>
<title>Aprenda Matemática Usando JavaScript</title>
</head>
<body>
<script type="text/javascript">
// os coeficientes
var a, b, c;
// as duas raizes, a imaginaria e o discriminante
var raiz1, raiz2, imaginaria, discriminante;
// vamos pedir para o usuário informar os valores dos coeficientes
a = parseFloat(window.prompt("Valor do coeficiente a: "));
b = parseFloat(window.prompt("Valor do coeficiente b: "));
c = parseFloat(window.prompt("Valor do coeficiente c: "));
// vamos calcular o discriminante
discriminante = (b * b) - (4 * a * c);
// a equação possui duas soluções reais?
if(discriminante > 0){
raiz1 = (-b + Math.sqrt(discriminante)) / (2 * a);
raiz2 = (-b - Math.sqrt(discriminante)) / (2 * a);
document.write("Existem duas raizes: x1 = " + raiz1
+ " e x2 = " + raiz2);
}
// a equação possui uma única solução real?
else if(discriminante == 0){
raiz1 = raiz2 = -b / (2 * a);
document.write("Existem duas raizes iguais: x1 = "
+ raiz1 + " e x2 = " + raiz2);
}
// a equação não possui solução real?
else if(discriminante < 0){
raiz1 = raiz2 = -b / (2 * a);
imaginaria = Math.sqrt(-discriminante) / (2 * a);
document.write("Existem duas raízes complexas: x1 = " +
raiz1 + " + " + imaginaria + " e x2 = " + raiz2
+ " - " + imaginaria);
}
</script>
</body>
</html>
Ao executar este código JavaScript nós teremos o seguinte resultado: Valor do coeficiente a: 1 Valor do coeficiente b: 2 Valor do coeficiente c: -3 Existem duas raizes: x1 = 1 e x2 = -3 |
Python ::: Python para Engenharia ::: Engenharia Civil - Concreto, Concreto Armado e Concretos Especiais |
Cálculo de estribos em vigas de concreto armado usando Python - Verificação da compressão diagonal do concretoQuantidade de visualizações: 232 vezes |
|
No dimensionamento de vigas de concreto armado à força cortante, ou seja, aos esforços de cisalhamento, nós adotamos, de acordo com recomendações da ABNT NBR 6118 (Projeto de estruturas de concreto armado), o modelo de treliça clássica de Ritter-Mörsh, na qual é suposto que uma carga aplicada num ponto qualquer de uma viga de concreto armado, chegue até os apoios percorrendo o caminho de uma treliça. Recordemos ainda que na treliça clássica de Ritter-Mörsh o ângulo de inclinação das bielas comprimidas é igual à 45°. Neste modelo de treliça, a compressão do banzo superior é resistida pelo concreto, enquanto a tração do banzo inferior é resistida pelo aço. As diagonais comprimidas também são resistidas pelo concreto, cabendo ao aço (estribos) o papel de reforçar as diagonais tracionadas. Notem que usei "reforçar", pois o concreto oferece também uma parcela de resistência à tração nestas diagonais. Sendo assim, um dos primeiros passos no cálculo e detalhamento das armaduras transversais, ou seja, a armadura de cisalhamento de uma viga de concreto armado, é a verificação da compressão diagonal do concreto. Neste passo nós verificamos se as bielas comprimidas resistem ao esforço cortante solicitante de projeto VSd. A verificação da compressão diagonal do concreto no Modelo I (no qual o ângulo α, que é o ângulo entre os estribos e o eixo longitudinal da viga, pode ser considerado entre 45º e 90º) pode ser realizada por meio da seguinte fórmula: \[V_\text{Rd2} = 0,27 \cdot \alpha_\text{v2} \cdot f_\text{cd} \cdot b_w \cdot d \] Onde: fcd é a resistência de cálculo do concreto, em kN/cm2; bw é a largura da viga, em centímetros; d é a altura útil da viga em centímetros; Já o αv2 pode ser calculado pela seguinte fórmula: \[\alpha_\text{v2} = 1 - \frac{f_\text{ck}}{250}\] Onde: fck é a resistência característica do concreto, em Mpa. Veja agora o código Python :
# método principal
def main():
# vamos pedir para o usuário informar a altura da viga
altura = float(input("Informe a altura h da viga em cm: "))
# vamos pedir para o usuário informar a largura da viga
largura = float(input("Informe a largura bw da viga em cm: "))
# vamos calcular a altura útil da viga
# aqui eu usei 0.9 mas alguns engenheiros usam 0.95
altura_util = 0.9 * altura
# vamos pedir para o usuário informar o FCK do concreto
fck = float(input("Informe o FCK do concreto em Mpa: "))
# vamos ler o coeficiente de minoração do concreto
yc = float(input("Informe o coeficiente de minoração yc: "))
# vamos solicitar o esforço cortante solicitante VSk
VSk = float(input("Informe o esforço cortante solicitante em kN: "))
# vamos ler o coeficiente de majoração das cargas
yf = float(input("Informe o coeficiente de majoração yf: "))
# vamos calcular o esforço cortante solicitante de cálculo VSd
VSd = yf * VSk
# agora vamos calcular o fcd do concreto
fcd = fck / yc
# vamos calcular o alfa v2
av2 = 1 - (fck / 250)
# finalmente vamos calcular o VRd2 no Modelo de Cálculo I
VRd2 = 0.27 * av2 * (fcd / 10) * largura * altura_util
# vamos mostrar os resultados
print("\n------ RESULTADOS -----------------------------")
print("O fcd do concreto é: {0} Mpa".format(round(fcd, 4)))
print("O valor de av2 é: {0}".format(round(av2, 4)))
print("O valor de VRd2 é: {0} kN".format(round(VRd2, 4)))
print("O valor de VSd é: {0} kN".format(round(VSd, 4)))
# vamos testar se as bielas de compressão não serão esmagadas
if (VSd <= VRd2):
print("VSd <= VRd2: As bielas de compressão RESISTEM")
else:
print("VSd > VRd2: As bielas de compressão NÃO RESISTEM")
if __name__ == "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Informe a altura h da viga em cm: 40 Informe a largura bw da viga em cm: 20 Informe o FCK do concreto em Mpa: 25 Informe o coeficiente de minoração yc: 1.4 Informe o esforço cortante solicitante em kN: 75 Informe o coeficiente de majoração yf: 1.4 ------ RESULTADOS ----------------------------- O fcd do concreto é: 17.8571 Mpa O valor de av2 é: 0.9 O valor de VRd2 é: 312.4286 kN O valor de VSd é: 105.0 kN VSd <= VRd2: As bielas de compressão RESISTEM |
Dart ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como testar se um ponto está dentro de um círculo em Dart - Desenvolvimento de Games com DartQuantidade de visualizações: 874 vezes |
|
Quando estamos trabalhando com computação gráfica, geometria e trigonometria ou desenvolvimento de jogos em Dart, é comum precisarmos verificar se um determinado ponto (uma coordenada x, y) está contido dentro de um círculo. Para melhor entendimento, veja a imagem a seguir: 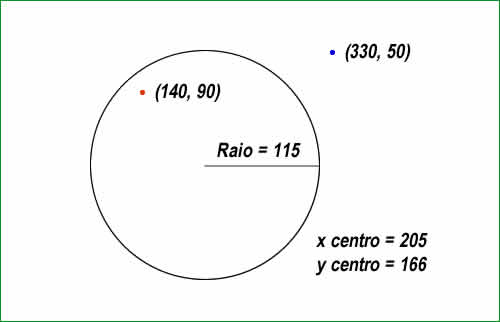 Veja que temos um círculo com raio igual a 115 e com centro nas coordenadas (x = 205; y = 166). Temos também dois pontos. O ponto vermelho está nas coordenadas (x = 140; y = 90) e o ponto azul está nas coordenadas (x = 330; y = 500. Como podemos ver na imagem, o ponto vermelho está dentro do círculo, enquanto o ponto azul está fora. E nosso intenção nesta dica é escrever o código Dart que permite fazer essa verificação. Tenha em mente que está técnica é muito útil para o teste de colisões no desenvolvimento de games. Veja o código completo para o exemplo:
// Vamos importar a biblioteca dart:io
import "dart:io";
// vamos importar a biblioteca dart:math
import "dart:math";
// vamos declarar a classe Circulo
class Circulo{
double xc;
double yc;
double raio;
// construtor da classe Circulo
Circulo(double xc, double yc, double raio){
this.xc = xc; // x do centro
this.yc = yc; // y do centro
this.raio = raio; // raio do círculo
}
}
// agora vamos declarar a classe Ponto
class Ponto{
double x;
double y;
// construtor da classe Ponto
Ponto(double x, double y){
this.x = x; // coordenada x
this.y = y; // coordenada y
}
}
void main(){
// variáveis que vamos usar na resolução do problema
Circulo c;
Ponto p;
double dx, dy;
// vamos criar um objeto Circulo
c = new Circulo(205, 166, 115);
// vamos criar um objeto Ponto
p = new Ponto(140, 90);
// vamos verificar se o ponto está dentro do
// círculo
dx = p.x - c.xc;
dy = p.y - c.yc;
if((pow(dx, 2) + pow(dy, 2)) < pow(c.raio, 2)){
stdout.write("O ponto está dentro do círculo");
}
else{
stdout.write("O ponto NÃO está dentro do círculo");
}
}
Ao executar este código Dart nós teremos o seguinte resultado: O ponto está dentro do círculo. Experimente com círculos de raios e coordenadas centrais diferentes e também com pontos em várias coordenadas e veja como os resultados são interessantes. |
Python ::: Dicas & Truques ::: Ordenação e Pesquisa (Busca) |
Python Insertion Sort - Como ordenar um vetor de inteiros usando a ordenação Insertion Sort (Ordenação por Inserção)Quantidade de visualizações: 3927 vezes |
|
Nesta dica veremos como implementar a ordenação Insertion Sort, Insertion-Sort, ou Ordenação por Inserção na linguagem Python. A ordenação Insertion Sort, Insertion-Sort, ou Ordenação por Inserção, possui uma complexidade de tempo de execução igual à ordenação Bubble Sort (Ordenação da Bolha), ou seja, O(n2). Embora mais rápido que o Bubble Sort, e ser um algorítmo de ordenação quadrática, a ordenação Insertion Sort é bastante eficiente para problemas com pequenas entradas, sendo o mais eficiente entre os algoritmos desta ordem de classificação, porém, nunca recomendada para um grande conjunto de dados. A forma mais comum para o entendimento da ordenação Insertion Sort é compará-la com a forma pela qual algumas pessoas organizam um baralho num jogo de cartas. Imagine que você está jogando cartas. Você está com as cartas na mão e elas estão ordenadas. Você recebe uma nova carta e deve colocá-la na posição correta da sua mão de cartas, de forma que as cartas obedeçam à ordenação. A cada nova carta adicionada à sua mão de cartas, a nova carta pode ser menor que algumas das cartas que você já tem na mão ou maior, e assim, você começa a comparar a nova carta com todas as cartas na sua mão até encontrar sua posição correta. Você insere a nova carta na posição correta, e, novamente, a sua mão é composta de cartas totalmente ordenadas. Então, você recebe outra carta e repete o mesmo procedimento. Então outra carta, e outra, e assim por diante, até não receber mais cartas. Esta é a ideia por trás da ordenação por inserção. Percorra as posições do vetor (array), começando com o índice 1 (um). Cada nova posição é como a nova carta que você recebeu, e você precisa inseri-la no lugar correto no sub-vetor ordenado à esquerda daquela posição. Vamos ver a implementação na linguagem Python agora? Observe o seguinte código, no qual temos um vetor de inteiros com os elementos {4, 6, 2, 8, 1, 9, 3, 0, 11}:
# método que permite ordenar o vetor de inteiros
# usando a ordenação Insertion Sort
def insertionSort(vetor):
# percorre todos os elementos do vetor começando
# pelo segundo elemento
for i in range(len(vetor)):
atual = vetor[i] # o valor atual a ser inserido
# começa a comparar com a célula à esquerda de i
j = i - 1
# enquanto vetor[j] estiver fora de ordem em relação
# a atual
while((j >= 0) and (vetor[j] > atual)):
# movemos vetor[j] para a direita e decrementamos j
vetor[j + 1] = vetor[j]
j = j - 1
# colocamos atual em seu devido lugar
vetor[j + 1] = atual
# função principal do programa
def main():
# cria uma lista de inteiros
valores = [4, 6, 2, 8, 1, 9, 3, 0, 11]
# exibimos o vetor na ordem original
print("Ordem original:\n")
for i in range(len(valores)):
print(valores[i], end = " ")
# vamos ordenar o vetor agora
insertionSort(valores)
# exibimos o vetor ordenado
print("\n\nOrdenado:\n")
for i in range(len(valores)):
print(valores[i], end = " ")
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Sem ordenação: 4 6 2 8 1 9 3 0 11 Ordenada usando Insertion Sort: 0 1 2 3 4 6 8 9 11 |
Revit C# ::: Dicas & Truques ::: Revit C# Windows Forms |
Como criar um formulário Windows Forms a partir do Revit C#Quantidade de visualizações: 785 vezes |
|
Nesta dica mostrarei os passos necessários para se criar uma aplicação Revit C# contendo uma formulário Windows Forms. O objetivo é demonstrar como o usuário pode interagir com os elementos do formulário para acessar e manipular objetos do Revit a partir de códigos C#. Antes de continuarmos, veja a janela Windows Forms que criamos logo abaixo:  Veja que temos um formulário contendo 6 Labels e 6 TextBox contendo as coordenadas inicias e finais de uma linha geométrica usada para criar um novo eixo na área de desenho do Revit. Ao informar as coordenadas e clicar o botão Desenhar Eixo, um novo objeto da classe Grid da Revit API é criado e desenhado no documento atual. Este código é muito útil para iniciantes em programação Revit C# porque mostra como acessar o documento ativo usando ActiveUIDocument e em seguida passar este objeto para uma outra classe C#. De posse deste objeto nós podemos realizar várias tarefas, entre elas criar uma nova linha geométrica usando Line.CreateBound() e, em seguida, criar um novo Grid usando Grid.Create(). Veja o código completo para uma macro chamada Estudos do tipo Aplicativo. Se tiver dificuldades para executar, chama a gente nos contatos na parte superior do site que teremos prazer em ajudá-lo. Eis a listagem do código C#:
using System;
using Autodesk.Revit.UI;
using Autodesk.Revit.DB;
using Autodesk.Revit.UI.Selection;
using System.Collections.Generic;
using System.Linq;
using System.Windows.Forms;
namespace Estudos {
[Autodesk.Revit.Attributes.Transaction(Autodesk.Revit.Attributes.
TransactionMode.Manual)]
[Autodesk.Revit.DB.Macros.AddInId("ED8EC6C4-9489-48F7-B04E-B45B5D1BEB12")]
public partial class ThisApplication {
private void Module_Startup(object sender, EventArgs e) {
JanelaPrincipal janela = new JanelaPrincipal();
janela.uidoc = this.ActiveUIDocument;
janela.ShowDialog();
}
private void Module_Shutdown(object sender, EventArgs e) {
// para fazer alguma limpeza de memória ou algo assim
}
#region Revit Macros generated code
private void InternalStartup() {
this.Startup += new System.EventHandler(Module_Startup);
this.Shutdown += new System.EventHandler(Module_Shutdown);
}
#endregion
}
// classe para representar o formulário
public class JanelaPrincipal : System.Windows.Forms.Form {
public UIDocument uidoc;
public System.Windows.Forms.TextBox txtX0;
public System.Windows.Forms.TextBox txtY0;
public System.Windows.Forms.TextBox txtZ0;
public System.Windows.Forms.TextBox txtX1;
public System.Windows.Forms.TextBox txtY1;
public System.Windows.Forms.TextBox txtZ1;
// construtor da classe
public JanelaPrincipal() {
this.Text = "Meu Formulário Revit C# Windows Forms"; // título da janela
this.Width = 390; // largura da janela
this.Height = 240; // altura da janela
// define a posição atual da janela
this.StartPosition = FormStartPosition.CenterScreen;
// vamos criar quatro labels e quatro caixas de texto
Label label1 = new Label();
label1.Text = "X Inicial:";
label1.Location = new System.Drawing.Point(20, 20);
label1.Height = 15;
label1.Width = 80;
Label label2 = new Label();
label2.Text = "Y Inicial:";
label2.Location = new System.Drawing.Point(120, 20);
label2.Height = 15;
label2.Width = 80;
Label label3 = new Label();
label3.Text = "Z Inicial:";
label3.Location = new System.Drawing.Point(220, 20);
label3.Height = 15;
label3.Width = 80;
txtX0 = new System.Windows.Forms.TextBox();
txtX0.Location = new System.Drawing.Point(20, 40);
txtX0.Width = 80;
txtX0.Height = 15;
txtY0 = new System.Windows.Forms.TextBox();
txtY0.Location = new System.Drawing.Point(120, 40);
txtY0.Width = 80;
txtY0.Height = 15;
txtZ0 = new System.Windows.Forms.TextBox();
txtZ0.Location = new System.Drawing.Point(220, 40);
txtZ0.Width = 80;
txtZ0.Height = 15;
Label label4 = new Label();
label4.Text = "X Final:";
label4.Location = new System.Drawing.Point(20, 80);
label4.Height = 15;
label4.Width = 80;
Label label5 = new Label();
label5.Text = "Y Final:";
label5.Location = new System.Drawing.Point(120, 80);
label5.Height = 15;
label5.Width = 80;
Label label6 = new Label();
label6.Text = "Z Final:";
label6.Location = new System.Drawing.Point(220, 80);
label6.Height = 15;
label6.Width = 80;
txtX1 = new System.Windows.Forms.TextBox();
txtX1.Location = new System.Drawing.Point(20, 97);
txtX1.Width = 80;
txtX1.Height = 15;
txtY1 = new System.Windows.Forms.TextBox();
txtY1.Location = new System.Drawing.Point(120, 97);
txtY1.Width = 80;
txtY1.Height = 15;
txtZ1 = new System.Windows.Forms.TextBox();
txtZ1.Location = new System.Drawing.Point(220, 97);
txtZ1.Width = 80;
txtZ1.Height = 15;
// botão que desenha o eixo nas coordenadas indicadas
Button button1 = new Button();
button1.Text = "Desenhar Eixo";
button1.Location = new System.Drawing.Point(95, 160);
button1.Width = 150;
button1.Click += new System.EventHandler(DesenharEixo);
// botão que fecha a janela
Button button2 = new Button();
button2.Text = "Fechar";
button2.Location = new System.Drawing.Point(265, 160);
button2.Width = 80;
button2.Click += new System.EventHandler(FecharJanela);
// adiciona os controles à janela
this.Controls.Add(label1);
this.Controls.Add(label2);
this.Controls.Add(label3);
this.Controls.Add(label4);
this.Controls.Add(label5);
this.Controls.Add(label6);
this.Controls.Add(txtX0);
this.Controls.Add(txtY0);
this.Controls.Add(txtZ0);
this.Controls.Add(txtX1);
this.Controls.Add(txtY1);
this.Controls.Add(txtZ1);
this.Controls.Add(button1);
this.Controls.Add(button2);
}
// função usada para desenhar um novo eixo no documento atual
private void DesenharEixo(object sender, System.EventArgs e) {
// primeiro obtemos uma referência ao documento atual
Document doc = uidoc.Document;
// criamos a linha geométrica para posicionar o eixo
XYZ inicio = new XYZ(Double.Parse(txtX0.Text), Double.Parse(txtY0.Text),
Double.Parse(txtZ0.Text));
XYZ final = new XYZ(Double.Parse(txtX1.Text), Double.Parse(txtY1.Text),
Double.Parse(txtZ1.Text));
// construímos a linha
Line linhaGeometrica = Line.CreateBound(inicio, final);
// iniciamos uma nova transação
using(Transaction t= new Transaction(doc)) {
t.Start("Criar um novo Grid");
Grid grid = Grid.Create(doc, linhaGeometrica);
t.Commit();
}
}
// função usada para fechar a janela
private void FecharJanela(object sender, System.EventArgs e) {
this.Close();
}
}
}
Não se esqueça de adicionar referências a System.Windows.Forms e System.Drawing. Basta, dentro do SharpDevelop, ir no menu Projeto -> Adicionar Referência. |
Python ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Como criar um laço while() infinito na linguagem PythonQuantidade de visualizações: 10135 vezes |
|
Nesta dica eu mostrarei como é possível criar um laço (loop) while infinito em Python. Esta técnica é útil para as situações nas quais queremos interagir com o usuário do nosso programa até que um determinado valor seja informado. No exemplo abaixo temos um laço while() que será executado até que o texto "fim" seja informado pelo usuário. Veja o código completo:
def main():
while True:
frase = input("Digite uma frase: ");
print("Você digitou: ", frase)
# vamos sair do laço
if frase == "fim":
print("Você acaba de sair do laço while()")
break
if __name__== "__main__":
main()
Ao executar este código nós teremos o seguinte resultado: Digite uma frase: Estou estudando Python Você digitou: Estou estudando Python Digite uma frase: Preciso viajar amanhã Você digitou: Preciso viajar amanhã Digite uma frase: fim Você digitou: fim Você acaba de sair do laço while() |
Nossas 20 dicas & truques de programação mais populares |
Você também poderá gostar das dicas e truques de programação abaixo |
|
JavaScript - Como testar se todos os elementos de um array satisfazem uma condição em JavaScript usando a função every() GNU Octave - Como calcular o cosseno de um ângulo em GNU Octave usando a função cos() - Calculadora de cosseno em Octave Java - Como percorrer uma árvore binária em Java usando o algorítmo depth-first search (DFS) recursivo PHP - Manipulação de texto em PHP - Como acessar e modificar os caracteres individuais de uma string |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





