Ruby ::: Dicas & Truques ::: Programação Orientada a Objetos |
Como acessar variáveis de instâncias para leitura em Ruby sem a necessidade de métodos acessores usando a função attr_readerQuantidade de visualizações: 6947 vezes |
|
Por padrão, variáveis de instância em Ruby só podem ser acessadas usando métodos acessores, ou seja, uma variável de instância @nome deve ser lida usando um método obter_nome. É possível dispensar o uso de métodos acessores empregando o método attr_reader nos nomes das variáveis que poderão ser acessadas, para leitura, é claro. Veja um exemplo:
# Definição da classe Cliente
class Cliente
attr_reader :nome, :idade
def initialize(nome, idade)
@nome = nome
@idade = idade
end
def obter_nome
@nome
end
def obter_idade
@idade
end
end
# Cria uma instância da classe Cliente e inicializa as
# variáveis de instância @nome e @idade
cliente = Cliente.new("Osmar J. Silva", 35)
# Acessa as variáveis de instância sem a necessidade de
# métodos acessórios
puts cliente.nome
puts cliente.idade
Sem o uso do método attr_reader, a linha: puts cliente.nome causaria o seguinte erro: teste.rb:25: undefined method `nome' for #<Cliente:0x27f540c @nome="Osmar J. S ilva", @idade=35> (NoMethodError) |
PHP ::: Dicas & Truques ::: Strings e Caracteres |
Como converter uma string para letras maiúsculas em PHP usando as funções strtoupper() e mb_strtoupper()Quantidade de visualizações: 121 vezes |
As funções strtoupper() e mb_strtoupper() do PHP nos ajuda quando precisamos transformar uma string inteira para letras maiúsculas. Veja o seguinte exemplo:<?php // uma frase contendo letras minúsculas $frase = "PHP? Eu gosto de PHP"; echo "A frase é: " . $frase . "\n"; // agora vamos transformá-la em letras // maiúsculas $frase = strtoupper($frase); echo "A frase em letras maiúsculas é: " . $frase; ?> Ao executar este código PHP nós teremos o seguinte resultado: A frase é: PHP? Eu gosto de PHP A frase em letras maiúsculas é: PHP? EU GOSTO DE PHP A função mb_strtoupper(), por sua vez, é usada quando a palavra, frase ou texto contém acentuações. Nas versões mais recentes do PHP, a função strtoupper() sozinha não consegue converter caracteres minúsculas com acentos para caracteres maiúsculas acentuados. Por isso, a função mb_strtoupper() é usada. Veja: <?php // uma frase contendo letras minúsculas $frase = "Java? Não gosto muito de Java não"; echo "A frase é: " . $frase . "\n"; // agora vamos transformá-la em letras // maiúsculas $frase1 = strtoupper($frase); echo "Usando strtoupper(): " . $frase1; $frase2 = mb_strtoupper($frase, 'UTF-8'); echo "\nUsando mb_strtoupper(): " . $frase2; ?> Ao executar este código PHP nós teremos o seguinte resultado: A frase é: Java? Não gosto muito de Java não Usando strtoupper(): JAVA? NãO GOSTO MUITO DE JAVA NãO Usando mb_strtoupper(): JAVA? NÃO GOSTO MUITO DE JAVA NÃO Veja que usei o valor "UTF-8" como segundo argumento para a função mb_strtoupper(). Se necessário você pode fornecer o valor "ISO-8859-1" também. |
C# ::: Windows Forms ::: DataGridView |
Como retornar a quantidade de colunas em um DataGridView do C# Windows FormsQuantidade de visualizações: 9985 vezes |
A quantidade de colunas em um DataGridView pode ser obtida por meio da propriedade ColumnCount. Veja:
private void button2_Click(object sender, EventArgs e){
// vamos adicionar três colunas no DataGridView
dataGridView1.Columns.Add("cidade", "Cidade");
dataGridView1.Columns.Add("estado", "Estado");
dataGridView1.Columns.Add("populacao", "População");
// vamos adicionar três linhas
dataGridView1.Rows.Add("Goiânia", "GO", "3.453,39");
dataGridView1.Rows.Add("Cuiabá", "MT", "1.876,12");
dataGridView1.Rows.Add("Curitiba", "PR", "5.346,98");
// vamos obter a quantidade de colunas no DataGridView
int quant_colunas = dataGridView1.ColumnCount;
// exibe o resultado
MessageBox.Show("O DataGridView contém " +
quant_colunas + " colunas");
}
É possível também usar a propriedade ColumnCount para definir a quantidade de colunas em um DataGridView: dataGridView1.ColumnCount = 6; Há algumas considerações importantes sobre a propriedade ColumnCount: 1) Se seu valor for definido como 0, todas as colunas do DataGridView serão removidas; 2) Se o novo valor for menor que o valor atual, as colunas excedentes serão removidas no final da coleção Columns; 3) Se o novo valor for maior que o valor atual, as novas colunas serão adicionadas no final da coleção Columns; 4) Se tentarmos alterar o valor desta propriedade após a definição da propriedade DataSource, uma exceção InvalidOperationException será lançada. |
Java ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cateto adjascente dadas as medidas da hipotenusa e do cateto oposto em JavaQuantidade de visualizações: 1431 vezes |
|
Nesta dica mostrarei como podemos tirar proveito do Teorema de Pitágoras para obter a medida do cateto adjascente quando temos as medidas da hipotenusa e do cateto oposto. Este teorema diz que "o quadrado da hipotenusa é igual à soma dos quadrados dos catetos", o que torna a nossa tarefa, na linguagem Java, muito fácil. Comece observando a imagem a seguir:  Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. A medida da hipotenusa é, sem arredondamentos, 36.056 metros. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras): \[c^2 = a^2 + b^2\] Tudo que temos que fazer é mudar a fórmula para: \[b^2 = c^2 - a^2\] Veja que agora o quadrado do cateto adjascente é igual ao quadrado da hipotenusa menos o quadrado do cateto oposto. Não se esqueça de que a hipotenusa é o maior lado do triângulo retângulo. Veja agora como esse cálculo é feito em linguagem Java:
package arquivodecodigos;
public class Estudos{
public static void main(String args[]){
double c = 36.056; // medida da hipotenusa
double a = 20; // medida do cateto oposto
// agora vamos calcular a medida da cateto adjascente
double b = Math.sqrt(Math.pow(c, 2) - Math.pow(a, 2));
// e mostramos o resultado
System.out.println("A medida do cateto adjascente é: " +
b);
}
}
Ao executar este código Java nós teremos o seguinte resultado: A medida do cateto adjascente é: 30.00058559428465 Como podemos ver, o resultado retornado com o código Java confere com os valores da imagem apresentada. |
C ::: C para Engenharia ::: Hidrologia e Hidráulica |
Como calcular o volume de chuvas em C - Fórmula do cálculo do volume de chuvas em CQuantidade de visualizações: 455 vezes |
|
O estudo da Hidrologia passa, necessariamente, pelo cálculo do volume de chuvas em uma determinada região, ou bacia hidrológica. Assim, é comum ouvirmos alguém dizer que, em um determinado local, choveu 100 mm durante um determinado período. Mas o que isso significa? O mês mais chuvoso em Goiânia é dezembro, com média de 229 milímetros de precipitação de chuva. Isso significa que, em uma área de 1 m2, a lâmina de água formada pela chuva que cai apresenta uma altura de 229 milímetros. Como sabemos que o volume é a área multiplicada pela altura, tudo que temos a fazer é considerar a área de 1 m2 multiplicada pela altura da lâmina de água (convertida também para metros). Veja a fórmula: \[\text{Volume} = \text{(Área da Base) x Altura}\] Lembre-se de que volume pode ser retornado em litros, ou seja, 1 m3 = 1000 litros. Veja agora o código C completo que pede para o usuário informar a precipitação da chuva, ou seja, a altura da lâmina de água em milímetros e retorna o volume de água em litros.
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]) {
// variáveis usadas na resolução do problema
float altura_lamina, volume_chuva;
// vamos pedir para o usuário informar a altura da lâmina
// de água em milímetros
printf("Altura da lâmina de água em milímetros: ");
scanf("%f", &altura_lamina);
// o primeiro passo é converter os milímetros da lâmina de água
// para metros
altura_lamina = altura_lamina / 1000.0;
// agora que já temos a altura da lâmina em metros, vamos multiplicar
// pela base (1 metro quadrado) para obtermos o volume da chuva por
// metro quadrado
volume_chuva = (altura_lamina * 1.0) * 1000.0;
// vamos mostrar o resultado
printf("O volume da chuva é: %f litros para cada metro quadrado",
volume_chuva);
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: Altura da lâmina de água em milímetros: 229 O volume da chuva é: 229.0 litros para cada metro quadrado Qual é o volume de 1 mm de chuva? A altura pluviométrica é a espessura da lâmina d'água precipitada que cobre a região atingida pela chuva. Geralmente a unidade de medição é o milímetro (mm) porque o aparelho que mede a chuva, o pluviômetro, é lido em milímetros. O pluviômetro é um aparelho meteorológico destinado a medir, em milímetros, a altura da lâmina de água gerada pela chuva que caiu numa área de 1 m2. 1 mm de chuva equivale a 1 litro de água, ou 1 dm3, considerando a área de 1 m2. |
Java ::: Java para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como somar os elementos da diagonal principal de uma matriz em JavaQuantidade de visualizações: 2949 vezes |
|
A Matriz quadrada é um tipo especial de matriz que possui o mesmo número de linhas e o mesmo número de colunas, ou seja, dada uma matriz Anxm, ela será uma matriz quadrada se, e somente se, n = m, onde n é o número de linhas e m é o número de colunas. Em geral as matrizes quadradas são chamadas de Matrizes de Ordem n, onde n é o número de linhas e colunas. Dessa forma, uma matriz de ordem 4 é uma matriz que possui 4 linhas e quatro colunas. Toda matriz quadrada possui duas diagonais, e elas são muito exploradas tanto na matemática quanto na construção de algorítmos. Essas duas diagonais são chamadas de Diagonal Principal e Diagonal Secundária. A diagonal principal de uma matriz quadrada une o seu canto superior esquerdo ao canto inferior direito. Veja: 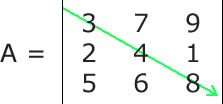 Nesta dica veremos como calcular a soma dos valores dos elementos da diagonal principal de uma matriz usando Java. Para isso, só precisamos manter em mente que a diagonal principal de uma matriz A é a coleção das entradas Aij em que i é igual a j. Assim, tudo que temos a fazer é converter essa regra para código Java. Veja um trecho de código Java completo no qual pedimos para o usuário informar os elementos da matriz e em seguida mostramos a soma dos elementos da diagonal superior:
package arquivodecodigos;
import java.util.Scanner;
public class Estudos{
public static void main(String[] args) {
// vamos fazer a leitura usando a classe Scanner
Scanner entrada = new Scanner(System.in);
// vamos declarar e construir uma matriz de três linhas e três colunas
int matriz[][] = new int[3][3];
int soma_diagonal = 0; // guarda a soma dos elementos na diagonal principal
// vamos ler os valores para os elementos da matriz
for(int i = 0; i < matriz.length; i++){ // linhas
for(int j = 0; j < matriz[0].length; j++){ // colunas
System.out.print("Informe o valor para a linha " + i + " e coluna "
+ j + ": ");
matriz[i][j] = Integer.parseInt(entrada.nextLine());
}
}
// vamos mostrar a matriz da forma que ela
// foi informada
System.out.println();
// percorre as linhas
for(int i = 0; i < matriz.length; i++){
// percorre as colunas
for(int j = 0; j < matriz[0].length; j++){
System.out.printf("%5d ", matriz[i][j]);
}
// passa para a próxima linha da matriz
System.out.println();
}
// vamos calcular a soma dos elementos da diagonal
// principal
for(int i = 0; i < matriz.length; i++){
for(int j = 0; j < matriz[0].length; j++){
if(i == j){
soma_diagonal = soma_diagonal + matriz[i][j];
}
}
}
// finalmente mostramos a soma da diagonal principal
System.out.println("\nA soma dos elementos da diagonal principal é: "
+ soma_diagonal);
}
}
Ao executar este código Java nós teremos o seguinte resultado:
Informe o valor para a linha 0 e coluna 0: 3
Informe o valor para a linha 0 e coluna 1: 7
Informe o valor para a linha 0 e coluna 2: 9
Informe o valor para a linha 1 e coluna 0: 2
Informe o valor para a linha 1 e coluna 1: 4
Informe o valor para a linha 1 e coluna 2: 1
Informe o valor para a linha 2 e coluna 0: 5
Informe o valor para a linha 2 e coluna 1: 6
Informe o valor para a linha 2 e coluna 2: 8
3 7 9
2 4 1
5 6 8
A soma dos elementos da diagonal principal é: 15
|
C ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular a área de um círculo em C dado o raio do círculoQuantidade de visualizações: 8919 vezes |
A área de um círculo pode ser calculada por meio do produto entre a constante PI e a medida do raio ao quadrado (r2). Comece analisando a figura abaixo: Sendo assim, temos a seguinte fórmula:  Onde A é a área, PI equivale a 3,14 (aproximadamente) e r é o raio do círculo. O raio é a medida que vai do centro até um ponto da extremidade do círculo. O diâmetro é a medida equivalente ao dobro da medida do raio, passando pelo centro do círculo e dividindo-o em duas partes. A medida do diâmetro é 2 * Raio. Veja agora um código C completo que calcula a área de um círculo mediante a informação do raio:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
// vamos definir o valor de PI
#define PI 3.14159265358979323846
int main(int argc, char *argv[]){
int raio;
printf("Informe o raio do círculo: ");
// efetua a leitura do raio
scanf("%d", &raio);
// calcula a área
double area = PI * pow(raio, 2);
// mostra o resultado
printf("A area do círculo de raio %d é igual a %f\n\n",
raio, area);
system("PAUSE");
return 0;
}
Ao executarmos este código nós teremos o seguinte resultado: Informe o raio do círculo: 5 A area do círculo de raio 5 é igual a 78.539816 A circunferência é um conjunto de pontos que estão a uma mesma distância do centro. Essa distância é conhecida como raio. A circunferência é estudada pela Geometria Analítica e, em geral, em um plano cartesiano. O círculo, que é formado pela circunferência e pelos infinitos pontos que preenchem seu interior, é estudado pela Geometria Plana, pois ele ocupa um espaço e pode ter sua área calculada, diferentemente da circunferência. |
Ruby ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como adicionar itens ao final de um array em Ruby usando o operador <<Quantidade de visualizações: 6578 vezes |
|
Nesta dica mostrarei como podemos usar o operador << da linguagem Ruby para adicionar novos elementos no final de um array. Veja o código completo para o exemplo:
# vamos criar um array de nomes
nomes = []
# Lê entrada até que o valor -1 seja
# fornecido
loop do
print "Digite um nome (-1 para sair): "
nome = gets.chomp
# vamos adicionar este nome no final do
# array
if nome != "-1"
nomes << nome # adiciona o nome ao array
end
# vamos sair do laço se o valor for "-1"
if nome == "-1"
break
end
end
# Exibe todos os valores do array
puts "\nOs nomes fornecidos foram:"
nomes.each do | nome |
puts nome
end
Ao executar este código Ruby nós teremos o seguinte resultado: Digite um nome (-1 para sair): FERNANDA Digite um nome (-1 para sair): LAURA Digite um nome (-1 para sair): ISADORA Digite um nome (-1 para sair): CINTIA Digite um nome (-1 para sair): -1 Os nomes fornecidos foram: FERNANDA LAURA ISADORA CINTIA |
C ::: Dicas & Truques ::: Strings e Caracteres |
Como acessar os caracteres de uma string individualmente usando índices na linguagem CQuantidade de visualizações: 9652 vezes |
Como em C uma string é vetor (array) de caracteres, tais caracteres podem ser acessados por meio de seu índice no vetor (um valor inteiro começando em 0). Este trecho de código mostra como esta tarefa pode ser realizada:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int main(int argc, char *argv[]){
char palavra[] = "Arquivo";
// vamos acessar o primeiro caractere da string
char letra = palavra[0];
printf("O primeiro caractere e %c\n", letra);
// vamos acessar o quinto caractere da string
letra = palavra[4];
printf("O quinto caractere e %c\n", letra);
puts("\n\n");
system("PAUSE");
return 0;
}
Ao executarmos este códigos nós teremos o seguinte resultado: O primeiro caractere e A O quinto caractere e i |
Java ::: Dicas & Truques ::: Data e Hora |
Como construir uma data no passado ou futuro em Java usando a classe GregorianCalendarQuantidade de visualizações: 8272 vezes |
Esta dica mostra como construir uma data no passado ou futuro na linguagem Java usando a classe GregorianCalendar, que é uma classe derivada e concreta da classe Calendar. Veja a linha na qual informamos a data a ser criada: Calendar data = new GregorianCalendar(2008, 11, 13); Aqui nós estamos usando o construtor da classe GregorianCalendar que requer três valores inteiros. O ano, o mês e o dia. O mês é informado como um valor inteiro na faixa de 0 a 11, ou seja, 0 para janeiro, 1 para fevereiro e assim por diante. Veja o exemplo:
package arquivodecodigos;
import java.util.*;
import java.text.*;
public class Estudos{
public static void main(String args[]){
// vamos construir a data "13/12/2008"
Calendar data = new GregorianCalendar(2008, 11, 13);
// vamos exibir o resultado
Format formato = new SimpleDateFormat(
"EEEE, dd 'de' MMMM 'de' yyyy");
System.out.println(formato.format(data.getTime()));
}
}
Ao executar este código Java nós teremos o seguinte resultado: Sábado, 13 de Dezembro de 2008 |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Delphi - Como converter strings em valores TDateTime usando as funções StrToDate() e StrToDateDef() do Delphi Java - Programação Orientada a Objetos em Java - Como usar o modificador static em suas aplicações Java MySQL - Como excluir a chave primária de uma tabela MySQL usando o comando ALTER TABLE DROP PRIMARY KEY JavaScript - Como retornar o nome ou tipo de exceção de um erro em JavaScript usando a propriedade name do objeto Error |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






