C++ ::: Desafios e Lista de Exercícios Resolvidos ::: Strings e Caracteres |
Exercícios Resolvidos de C++ - Como retornar o código ASCII associado a um caractere em C++ - Ler um caractere e retornar o código ASCII correspondenteQuantidade de visualizações: 650 vezes |
|
Pergunta/Tarefa: Escreva um programa C++ que pede para o usuário informar um caractere (letra ou número) e mostre o código ASCII correspondente. Sua saída deverá ser parecida com: Informe um caractere: A Você informou o caractere: A O código ASCII correspondente é: 65 Veja a resolução comentada deste exercício em C++:
#include <iostream>
using namespace std;
// função principal do programa
int main(int argc, char *argv[]){
// variáveis usadas na resolução do problema
char caractere;
int codigo;
// vamos pedir para o usuário informar uma letra, símbolo ou pontuação
cout << "Informe um caractere: ";
// vamos ler o caractere informado
cin >> caractere;
// agora vamos obter o código ASCII correspondente
codigo = (int)caractere;
// e mostramos o resultado
cout << "Você informou o caractere: " << caractere << endl;
cout << "O código ASCII correspondente é: " << codigo << endl;
cout << "\n" << endl;
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
O Código Padrão Americano para o Intercâmbio de Informação (do inglês American Standard Code for Information Interchange - ASCII, pronunciado [áski]) é um sistema de representação de letras, algarismos e sinais de pontuação e de controle, através de um sinal codificado em forma de código binário (cadeias de bits formada por vários 0 e 1), desenvolvido a partir de 1960, que representa um conjunto de 128 sinais: 95 sinais gráficos (letras do alfabeto latino, algarismos arábicos, sinais de pontuação e sinais matemáticos) e 33 sinais de controle, utilizando 7 bits para representar todos os seus símbolos. |
LISP ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Como usar o laço loop para contar de 1 até 10 em LispQuantidade de visualizações: 701 vezes |
|
A estrutura de repetição loop da linguagem Common Lisp é o laço mais simples fornecido pela linguagem. Este laço nos permite repetir uma ou mais instruções de código repetidamente, até que o comando return seja encontrado, o que faz com que o laço seja interrompido. Veja no trecho de código abaixo como podemos usar o laço loop da Common Lisp para contar e exibir os valores de 1 até 10:
(
; vamos declarar a variável que vamos usar
let (numero)
; vamos inicializar a variável com o valor 1
(setq numero 1)
; agora iniciamos o laço
(loop
; escrevemos o valor da variável
(write numero)
; aumentamos o valor da variável em 1
(setq numero (+ numero 1))
; provocamos uma quebra de linha
(terpri)
; e fazemos o teste da continuidade
(when (> numero 10) (return))
)
)
Ao executarmos este código Common Lisp nós teremos o seguinte resultado: 1 2 3 4 5 6 7 8 9 10 Veja que usamos a macro when para testar o ponto de parada do laço. Note ainda o uso da função terpri da Common Lisp para provocar uma quebra de linha na saída do programa. |
AngularJS ::: Angular / AngularJS + JavaScript ::: Diretivas AngularJS |
Tutorial AngularJS - Como usar a diretiva ng-init do AngularJSQuantidade de visualizações: 2328 vezes |
A diretiva ng-init do AngularJS é usada quando queremos criar uma varíável no escopo atual e inicializá-la com algum valor. Veja um exemplo de seu uso:
<div ng-app="" ng-init="codigo=350">
<h1>O próximo código é: {{codigo + 1}}</h1>
</div>
Quando você executar este exemplo, verá escrita a saída: O próximo código é: 351 Isso aconteceu porque usamos a diretiva ng-init para criar uma variável chamada "codigo" e definimos o seu valor inicial como 350. Então, dentro do elemento <h1>, nós acessamos a variável e aumentamos o seu valor em 1 antes de exibí-la. É importante observar que esta diretiva só é usada em situações nas quais queremos apenas fazer protótipos, exemplos ou testar alguma funcionalidade. Na prática, variáveis do escopo são inicializadas usando-se Components ou Controllers. Um outro uso da diretiva ng-init é para declarar e inicializar variáveis dentro do escopo de um ng-repeat. Veja:
<script type="text/javascript">
// vamos criar uma nova aplicação AngularJS
var app = angular.module('MinhaApp', []);
// vamos criar um novo controller
app.controller('MeuController', function($scope){
$scope.Livros = [
{titulo: "Java para a web", autor: "Osmar J. Silva"},
{titulo: "Aprenda AngularJS", autor: "José de Angelis"}
];
});
</script>
<div ng-app="MinhaApp" ng-controller="MeuController">
<div ng-repeat="livro in Livros" ng-init="ordem = ($index + 1)">
<h1>Ordem: {{ordem}} - Título: {{livro.titulo}} - Autor: {{livro.autor}}</h1>
</div>
</div>
Quando você abrir esta página, verá a seguinte saída: Ordem: 1 - Título: Java para a web - Autor: Osmar J. Silva Ordem: 2 - Título: Aprenda AngularJS - Autor: José de Angelis |
Java ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cateto adjascente dadas as medidas da hipotenusa e do cateto oposto em JavaQuantidade de visualizações: 1431 vezes |
|
Nesta dica mostrarei como podemos tirar proveito do Teorema de Pitágoras para obter a medida do cateto adjascente quando temos as medidas da hipotenusa e do cateto oposto. Este teorema diz que "o quadrado da hipotenusa é igual à soma dos quadrados dos catetos", o que torna a nossa tarefa, na linguagem Java, muito fácil. Comece observando a imagem a seguir:  Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. A medida da hipotenusa é, sem arredondamentos, 36.056 metros. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras): \[c^2 = a^2 + b^2\] Tudo que temos que fazer é mudar a fórmula para: \[b^2 = c^2 - a^2\] Veja que agora o quadrado do cateto adjascente é igual ao quadrado da hipotenusa menos o quadrado do cateto oposto. Não se esqueça de que a hipotenusa é o maior lado do triângulo retângulo. Veja agora como esse cálculo é feito em linguagem Java:
package arquivodecodigos;
public class Estudos{
public static void main(String args[]){
double c = 36.056; // medida da hipotenusa
double a = 20; // medida do cateto oposto
// agora vamos calcular a medida da cateto adjascente
double b = Math.sqrt(Math.pow(c, 2) - Math.pow(a, 2));
// e mostramos o resultado
System.out.println("A medida do cateto adjascente é: " +
b);
}
}
Ao executar este código Java nós teremos o seguinte resultado: A medida do cateto adjascente é: 30.00058559428465 Como podemos ver, o resultado retornado com o código Java confere com os valores da imagem apresentada. |
C ::: Desafios e Lista de Exercícios Resolvidos ::: C Básico |
Exercício Resolvido de C - Ler três números inteiros e indicar se eles estão em ordem crescente ou decrescenteQuantidade de visualizações: 1169 vezes |
|
Pergunta/Tarefa: Escreva um programa C que pede para o usuário informar três números inteiros e informa se eles estão em ordem crescente ou decrescente. Se os números estiverem em ordem crescente, escreva "Ordem Crescente". Se estiverem em ordem decrescente, escreva "Ordem Decrescente". Do contrário escreva "Sem ordem definida". Sua saída deverá ser parecida com: Primeiro número: 4 Segundo número: 8 Terceiro número: 11 Ordem Crescente Veja a resolução comentada deste exercício em C:
#include <stdio.h>
#include <stdlib.h>
#include <locale.h>
// função principal do programa
int main(int argc, char *argv[]){
// variáveis usadas na resolução do exercício
int a, b, c;
setlocale(LC_ALL,""); // para acentos do português
// vamos pedir para o usuário informar três números
printf("Primeiro número: ");
scanf("%d", &a);
printf("Segundo número: ");
scanf("%d", &b);
printf("Terceiro número: ");
scanf("%d", &c);
// os números estão em ordem crescente?
if (a < b && b < c){
printf("Ordem Crescente");
}
// os números estão em ordem decrescente?
else if (a > b && b > c){
printf("Ordem Decrescente");
}
// sem ordem definida
else{
printf("Sem ordem definida");
}
printf("\n\n");
system("PAUSE");
return 0;
}
|
Java ::: Dicas & Truques ::: Threads |
Threads em Java - O que são threads e como usá-las em seus programas JavaQuantidade de visualizações: 13604 vezes |
|
Uma thread é um fluxo de execução de uma determinada tarefa em um programa. Na programação tradicional, temos apenas um fluxo de execução que começa a executar no início do programa e vai até o final. Com o uso de threads podemos ter várias tarefas sendo executadas ao mesmo tempo, cada uma independente da outra. Em programas que contêm interfaces gráficas, o uso de múltiplos fluxos de execução (ou threads) é muito comum. Enquanto digitamos em uma caixa de texto, uma animação pode estar sendo executada ou um arquivo sendo baixado. O Java permite que tenhamos várias threads sendo executadas ao mesmo tempo. Cada tarefa (ou thread) é uma instância da interface Runnable. Esta interface descreve apenas um método: public void run();
// criamos uma classe que servirá como thread
class MinhaThread extends Thread{
private String nome;
public MinhaThread(String nome){
this.nome = nome;
}
public void run(){
for(int i = 1; i <= 20; i++){
System.out.println(nome + ": " + i);
}
}
}
public class Estudos{
public static void main(String[] args){
// vamos criar duas threads
MinhaThread t1 = new MinhaThread("Thread 1");
t1.start(); // chamamos o método start() e não run()
MinhaThread t2 = new MinhaThread("Thread 2");
t2.start(); // chamamos o método start() e não run()
System.exit(0);
}
}
Salve este código como Estudos.java, compile e execute. Veja que cada thread escreverá de 1 a 20 na tela. Observe como as duas threads se alternam em suas tarefas, ou seja, de tempos em tempos uma cede lugar para que a outra seja executada. Note também que, embora nossa classe tenha um método run() nós não o chamamos. O que fazemos é chamar o método start(), que torna a thread elegível para ser executada a qualquer momento. Uma outra forma de criarmos uma thread é fazer com que nossa classe implemente a interface Runnable. Veja:
// criamos uma classe que servirá como thread
class MinhaThread implements Runnable{
private String nome;
public MinhaThread(String nome){
this.nome = nome;
}
public void run(){
for(int i = 1; i <= 20; i++){
System.out.println(nome + ": " + i);
}
}
}
public class Estudos{
public static void main(String[] args){
// vamos criar duas threads
MinhaThread mt1 = new MinhaThread("Thread 1");
Thread t1 = new Thread(mt1);
t1.start();
MinhaThread mt2 = new MinhaThread("Thread 2");
Thread t2 = new Thread(mt2);
t2.start();
System.exit(0);
}
}
O funcionamento do código é o mesmo. A diferença é que agora, a classe usada como thread implementa a interface Runnable. A forma de criação da thread também foi alterada. Agora nós criamos instâncias de Thread fornecendo nossa classe thread como argumento e chamamos o método start da classe Thread e não de nossa própria classe, como fizemos anteriormente. |
C++ ::: Desafios e Lista de Exercícios Resolvidos ::: Métodos, Procedimentos e Funções |
Exercício Resolvido de C++ - Uma função C++ que recebe um valor inteiro e informa se o mesmo é um número primoQuantidade de visualizações: 8961 vezes |
|
Exercícios Resolvidos de C++ - Uma função C++ que recebe um valor inteiro e informa se o mesmo é um número primo Pergunta/Tarefa: Um inteiro é um número primo se ele for divisível somente por 1 e por ele mesmo. Assim, 2, 3, 5 e 7 são primos, enquanto 4, 6, 8 e 9 não são. Escreva uma função C++ que recebe um valor inteiro e informe se o mesmo é um número primo. Você deverá usar a seguinte assinatura para a função:
bool primo(int valor){
// implementação aqui
}
Informe um valor inteiro: 7 O numero informado é primo Veja a resolução comentada deste exercício em C++:
#include <cstdlib>
#include <iostream>
using namespace std;
// protótipo da função primo()
bool primo(int);
int main(int argc, char *argv[]){
int numero;
setlocale(LC_ALL,""); // para acentos do português
cout << "Informe um valor inteiro: ";
cin >> numero;
// vamos verificar se o valor informado é um número primo
if(primo(numero)){
cout << "O numero informado é primo\n" << endl;
}
else{
cout << "O numero informado NÃO é primo\n" << endl;
}
system("PAUSE");
return EXIT_SUCCESS;
}
bool primo(int valor){
// se o valor fornecido for 7, a variável i do laço contará
// de 2 até 7 / 2 (divisão inteira), ou seja, 3. Se o
// módulo de 7 por qualquer um dos valores neste intervalo
// for igual a 0, então o número não é primo
for(int i = 2; i <= (valor / 2); i++){
if(valor % i == 0){
return false; // não é primo
}
}
return true;
}
|
Java ::: Dicas & Truques ::: Strings e Caracteres |
Como usar o método startsWith() da classe String do Java para verificar se uma string começa com uma substring - Como testar o conteúdo no início de uma stringQuantidade de visualizações: 289 vezes |
|
Em algumas situações gostaríamos de verificar se uma palavra, frase ou texto começa com uma determinada substring. Para isso podemos usar o método startsWith() da classe String da linguagem Java. Veja um código completo no qual verificamos se um endereço de um site na internet começa com "https":
package arquivodecodigos;
public class Estudos{
public static void main(String[] args){
String site = "https://www.arquivodecodigos.com.br";
if(site.startsWith("https")){
System.out.println("Este site parece ser seguro.");
}
else{
System.out.println("Este site não parece ser seguro.");
}
System.exit(0);
}
}
Ao executarmos este código nós teremos o seguinte resultado: Este site parece ser seguro. |
Java ::: Estruturas de Dados ::: Árvore Binária e Árvore Binária de Busca |
Estruturas de dados em Java - Como fazer a travessia de uma árvore binária de busca em Java usando o percurso em-ordem (in-order, In-ordem ou ordem simétrica)Quantidade de visualizações: 4983 vezes |
Antes de discutirmos o percurso in-order, veja a árvore binária de busca na figura abaixo: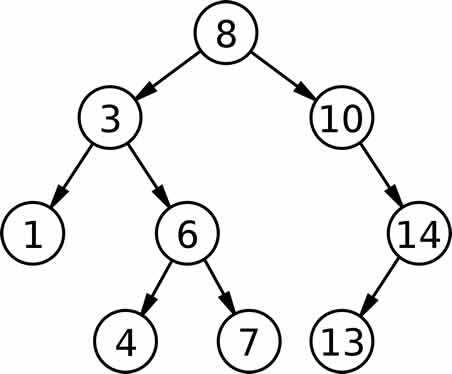 Esta árvore possui 9 nós e obedece à regra de que os nós com valores menores que o nó pai ficam à sua esquerda, e aqueles com nós maiores que o nó pai, ficam à sua direita. O percurso em ordem é usado quando queremos exibir os valores dos nós da árvore binária de busca em ordem ascendente. Neste tipo de percurso nós visitamos primeiramente a sub-árvore da esquerda, então o nó atual e finalmente a sub-árvore à direita do nó atual. É importante notar que esta travessia é feita por meio de um método recursivo. Veja o código completo para o exemplo: Código para No.java:
package arvore_binaria;
public class No {
private int valor; // valor armazenado no nó
private No esquerdo; // filho esquerdo
private No direito; // filho direito
// construtor do nó
public No(int valor){
this.valor = valor;
this.esquerdo = null;
this.direito = null;
}
public int getValor() {
return valor;
}
public void setValor(int valor) {
this.valor = valor;
}
public No getEsquerdo() {
return esquerdo;
}
public void setEsquerdo(No esquerdo) {
this.esquerdo = esquerdo;
}
public No getDireito() {
return direito;
}
public void setDireito(No direito) {
this.direito = direito;
}
}
Código para ArvoreBinariaBusca.java:
package arvore_binaria;
public class ArvoreBinariaBusca {
private No raiz; // referência para a raiz da árvore
// método usado para inserir um novo nó na árvore
// retorna true se o nó for inserido com sucesso e false
// se o elemento
// não puder ser inserido (no caso de já existir um
// elemento igual)
public boolean inserir(int valor){
// a árvore ainda está vazia?
if(raiz == null){
// vamos criar o primeiro nó e definí-lo como a raiz da árvore
raiz = new No(valor); // cria um novo nó
}
else{
// localiza o nó pai do novo nó
No pai = null;
No noAtual = raiz; // começa a busca pela raiz
// enquanto o nó atual for diferente de null
while(noAtual != null){
// o valor sendo inserido é menor que o nó atual?
if(valor < noAtual.getValor()) {
pai = noAtual;
// vamos inserir do lado esquerdo
noAtual = noAtual.getEsquerdo();
}
// o valor sendo inserido é maior que o nó atual
else if(valor > noAtual.getValor()){
pai = noAtual;
// vamos inserir do lado direito
noAtual = noAtual.getDireito();
}
else{
return false; // um nó com este valor foi encontrado
}
}
// cria o novo nó e o adiciona como filho do nó pai
if(valor < pai.getValor()){
pai.setEsquerdo(new No(valor));
}
else{
pai.setDireito(new No(valor));
}
}
return true; // retorna true para indicar que o novo nó foi inserido
}
// método que permite disparar a travessia em-ordem
public void emOrdem(){
emOrdem(raiz);
}
// sobrecarga do método emOrdem com uma parâmetro (esta é a versão
// recursiva do método)
private void emOrdem(No raiz){
if(raiz == null){ // condição de parada
return;
}
// visita a sub-árvore da esquerda
emOrdem(raiz.getEsquerdo());
// visita o nó atual
System.out.print(raiz.getValor() + " ");
// visita a sub-árvore da direita
emOrdem(raiz.getDireito());
}
}
E agora o código para a classe principal:
package arvore_binaria;
import java.util.Scanner;
public class ArvoreBinariaTeste {
public static void main(String[] args) {
Scanner entrada = new Scanner(System.in);
// vamos criar um novo objeto da classe ArvoreBinariaBusca
ArvoreBinariaBusca arvore = new ArvoreBinariaBusca();
// vamos inserir 9 valores na árvore
for(int i = 0; i < 9; i++){
System.out.print("Informe um valor inteiro: ");
int valor = Integer.parseInt(entrada.nextLine());
// vamos inserir o nó e verificar o sucesso da operação
if(!arvore.inserir(valor)){
System.out.println("Não foi possível inserir." +
" Um elemento já contém este valor.");
}
}
// vamos exibir os nós da árvore usando o percurso in-order
System.out.println("\nPercurso in-order:");
arvore.emOrdem();
System.out.println("\n");
}
}
Ao executar este código teremos o seguinte resultado: Informe um valor inteiro: 8 Informe um valor inteiro: 3 Informe um valor inteiro: 10 Informe um valor inteiro: 1 Informe um valor inteiro: 6 Informe um valor inteiro: 14 Informe um valor inteiro: 4 Informe um valor inteiro: 7 Informe um valor inteiro: 13 Percurso in-order: 1 3 4 6 7 8 10 13 14 |
VisuAlg ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em VisuAlg dados dois pontos no plano cartesianoQuantidade de visualizações: 603 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem VisuAlg que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
algoritmo "Calcular o coeficiente angular de uma reta em VisuAlg"
var
// coordenadas dos dois pontos
x1, y1, x2, y2: real
// guarda o coeficiente angular
m: real
inicio
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos calcular o coeficiente angular
m <- (y2 - y1) / (x2 - x1)
// mostramos o resultado
escreva("O coeficiente angular é: ", m)
fimalgoritmo
Ao executar este código VisuAlg nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.6666666666666666 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
algoritmo "Calcular o coeficiente angular de uma reta em VisuAlg"
var
// coordenadas dos dois pontos
x1, y1, x2, y2: real
// guarda os comprimentos dos catetos oposto e adjascente
cateto_oposto, cateto_adjascente: real
// guarda o ângulo tetha (em radianos) e a tangente
tetha, tangente: real
inicio
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos obter o comprimento do cateto oposto
cateto_oposto <- y2 - y1
// e agora o cateto adjascente
cateto_adjascente <- x2 - x1
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
tetha <- ArcTan(cateto_oposto / cateto_adjascente)
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
tangente <- Tan(tetha)
// mostramos o resultado
escreva("O coeficiente angular é: ", tangente)
fimalgoritmo
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Nossas 20 dicas & truques de programação mais populares |
|
Java - Como construir uma data em Java usando o método set() da classe Calendar - Apostila Java Básico |
Você também poderá gostar das dicas e truques de programação abaixo |
|
JavaScript - Como converter uma string para letras minúsculas em JavaScript usando a função toLowerCase() do objeto String Delphi - Como obter a quantidade de caracteres em uma palavra ou texto usando a função Length() do Delphi |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





