Java ::: Desafios e Lista de Exercícios Resolvidos ::: Estruturas de Controle |
Exercício Resolvido de Java - Como testar se um ano é bissexto em Java - Um programa que lê um ano com quatro dígitos e informa se ele é bissexto ou nãoQuantidade de visualizações: 2641 vezes |
|
Pergunta/Tarefa: Chama-se ano bissexto o ano ao qual é acrescentado um dia extra, ficando ele com 366 dias, um dia a mais do que os anos normais de 365 dias, ocorrendo a cada quatro anos (exceto anos múltiplos de 100 que não são múltiplos de 400). Isto é feito com o objetivo de manter o calendário anual ajustado com a translação da Terra e com os eventos sazonais relacionados às estações do ano. O último ano bissexto foi 2012 e o próximo será 2016. Um ano é bissexto se ele for divisível por 4 mas não por 100, ou se for divisível por 400. Escreva um programa Java que pede ao usuário um ano com quatro dígitos e informa se ele é bissexto ou não. Sua saída deverá ser parecida com: Informe o ano: 2024 O ano informado é bissexto. Veja a resolução comentada deste exercício usando Java console:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
Scanner entrada = new Scanner(System.in);
// vamos solicitar que o usuário informe um ano
System.out.print("Informe o ano: ");
int ano = Integer.parseInt(entrada.nextLine());
// vamos verificar se o ano informado é bissexto
if(((ano % 4 == 0) && (ano % 100 != 0)) || (ano % 400 == 0)){
System.out.println("O ano informado é bissexto.");
}
else{
System.out.println("O ano informado não é bissexto.");
}
System.out.println("\n");
}
}
|
Portugol ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em Portugol dados dois pontos no plano cartesianoQuantidade de visualizações: 577 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem Portugol que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
// Calcular o coeficiente angular de uma reta em Portugol
programa {
// vamos incluir a biblioteca Matematica
inclua biblioteca Matematica --> mat
funcao inicio() {
// coordenadas dos dois pontos
real x1, y1, x2, y2
// guarda o coeficiente angular
real m
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1)
// mostramos o resultado
escreva("O coeficiente angular é: ", m)
}
}
Ao executar este código Portugol Webstudio nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.6666666666666666 No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Python ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como converter graus em radianos em Python - Trigonometria em PythonQuantidade de visualizações: 3111 vezes |
|
Quando estamos trabalhando com trigonometria na linguagem Python, é importante ficarmos atentos ao fato de que todos os métodos e funções trigonométricas em Python recebem seus argumentos em radianos, em vez de graus. Nesta dica veremos como converter graus em radianos (sem a chatice de ficar relembrando regra de três). Veja a fórmula abaixo: \[Radianos = Graus \times \frac{\pi}{180}\] Agora veja como esta fórmula pode ser escrita em código Python:
import math
# função principal do programa
def main():
# valor em graus
graus = 30
# obtém o valor em radianos
radianos = graus * (math.pi / 180)
# mostra o resultado
print(graus, "graus convertidos para",
"radianos é", radianos)
if __name__== "__main__":
main()
Ao executarmos este código Python nós teremos o seguinte resultado: 30 graus convertidos para radianos é 0.5235987755982988 Por fim, saiba que a linguagem Python nos oferece o método math.radians() que nos permite converter ângulos em graus para radianos. Meu propósito nesta dica foi mostrar a você como o cálculo de conversão pode ser escrito em Python. Em outras dicas dessa seção abordaremos o método math.radians(). |
C ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cateto oposto dadas as medidas da hipotenusa e do cateto adjascente em CQuantidade de visualizações: 3140 vezes |
|
Todos estamos acostumados com o Teorema de Pitágoras, que diz que "o quadrado da hipotenusa é igual à soma dos quadrados dos catetos". Baseado nessa informação, fica fácil retornar a medida do cateto oposto quando temos as medidas da hipotenusa e do cateto adjascente. Isso, claro, via programação em linguagem C. Comece observando a imagem a seguir:  Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. A medida da hipotenusa é, sem arredondamentos, 36.056 metros. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras): \[c^2 = a^2 + b^2\] Tudo que temos que fazer é mudar a fórmula para: \[a^2 = c^2 - b^2\] Veja que agora o quadrado do cateto oposto é igual ao quadrado da hipotenusa menos o quadrado do cateto adjascente. Não se esqueça de que a hipotenusa é o maior lado do triângulo retângulo. Veja agora como esse cálculo é feito em linguagem C:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(int argc, char *argv[]){
float c = 36.056; // medida da hipotenusa
float b = 30; // medida do cateto adjascente
// agora vamos calcular o comprimento da cateto oposto
float a = sqrt(pow(c, 2) - pow(b, 2));
// e mostramos o resultado
printf("A medida do cateto oposto é: %f", a);
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: A medida do cateto oposto é: 20.000877 Como podemos ver, o resultado retornado com o código C confere com os valores da imagem apresentada. |
PHP ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o seno de um número ou ângulo em PHP usando a função sin()Quantidade de visualizações: 1725 vezes |
|
Em geral, quando falamos de seno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função seno disponível nas linguagens de programação para calcular o seno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função seno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o seno é a razão entre o cateto oposto (oposto ao ângulo theta) e a hipotenusa, ou seja, o cateto oposto dividido pela hipotenusa. Veja a fórmula: \[\text{Seno} = \frac{\text{Cateto oposto}}{\text{Hipotenusa}} \] Então, se dividirmos 20 por 36.056 (na figura eu arredondei) nós teremos 0.5547, que é a razão entre o cateto oposto e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.5547. O resultado será 0.9828 (em radianos). Convertendo 0.9828 radianos para graus, nós obtemos 56.31º, que é exatamente o ângulo em graus entre o cateto oposto e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é seno na trigonometria, vamos entender mais sobre a função sin() da linguagem PHP. Esta função recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja: <?php // vamos calcular o seno de três números echo "Seno de 0 = " . sin(0); echo "<br>Seno de 1 = " . sin(1); echo "<br>Seno de 2 = " . sin(2); ?> Ao executar este código PHP nós teremos o seguinte resultado: Seno de 0 = 0 Seno de 1 = 0.8414709848079 Seno de 2 = 0.90929742682568 Note que calculamos os senos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função seno mostrada abaixo: 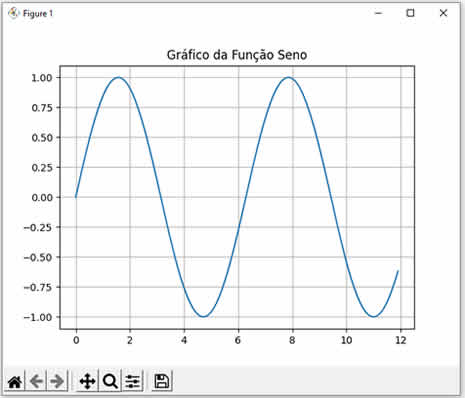 |
Java ::: Dicas & Truques ::: Strings e Caracteres |
Como transformar um StringBuffer em uma String usando o método toString() da classe StringBufferQuantidade de visualizações: 179 vezes |
|
Como já vimos em dicas anteriores, um objeto da classe String é imutável, ou seja, quando modificamos o conteúdo de uma String, o interpretador cria um novo objeto, copiando o conteúdo da string anterior para o objeto recém-criado. Já a classe StringBuffer é mutável, ou seja, podemos modificar o seu conteúdo sem a necessidade da criação de um novo objeto. Você ficará surpreso ao saber que não podemos atribuir uma variável do tipo StringBuffer em uma variável do tipo String e vice-versa. Ao tentarmos fazer isso, os seguintes erros de compilação são exibidos: a) error: incompatible types: StringBuffer cannot be converted to String b) error: incompatible types: String cannot be converted to StringBuffer Assim, sempre que for necessário converter um StringBuffer em uma String, temos que usar o seu método toString(). Veja:
package arquivodecodigos;
// Este exemplo mostra como converter um
// StringBuffer em uma String
public class Estudos{
public static void main(String[] args){
StringBuffer frase = new StringBuffer("Programação Java");
String resultado = frase.toString();
System.out.println(resultado);
System.exit(0);
}
}
|
JavaScript ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o seno de um número ou ângulo em JavaScript usando a função sin() do objeto MathQuantidade de visualizações: 8910 vezes |
|
Em geral, quando falamos de seno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função seno disponível nas linguagens de programação para calcular o seno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função seno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o seno é a razão entre o cateto oposto (oposto ao ângulo theta) e a hipotenusa, ou seja, o cateto oposto dividido pela hipotenusa. Veja a fórmula: \[\text{Seno} = \frac{\text{Cateto oposto}}{\text{Hipotenusa}} \] Então, se dividirmos 20 por 36.056 (na figura eu arredondei) nós teremos 0.5547, que é a razão entre o cateto oposto e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.5547. O resultado será 0.9828 (em radianos). Convertendo 0.9828 radianos para graus, nós obtemos 56.31º, que é exatamente o ângulo em graus entre o cateto oposto e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é seno na trigonometria, vamos entender mais sobre a função sin() da linguagem JavaScript. Esta função, disponível no objeto Math, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja:
<html>
<head>
<title>Estudos JavaScript</title>
</head>
<body>
<script type="text/javascript">
// vamos calcular o seno de três números
document.writeln("Seno de 0 = " + Math.sin(0));
document.writeln("<br>Seno de 1 = " + Math.sin(1));
document.writeln("<br>Seno de 2 = " + Math.sin(2));
</script>
</body>
</html>
Ao executar este código JavaScript nós teremos o seguinte resultado: Seno de 0 = 0 Seno de 1 = 0.8414709848078965 Seno de 2 = 0.9092974268256817 Note que calculamos os senos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função seno mostrada abaixo:  |
C# ::: Coleções (Collections) ::: List<T> |
Como percorrer os itens de uma List do C# usando o laço forQuantidade de visualizações: 570 vezes |
|
Em várias ocasiões nós precisamos percorrer os elementos de uma lista do C#. Para isso nós podemos usar o laço for e, dentro deste laço, acessar os elementos da lista individualmente usando o operador [] e o índice desejado. Veja o código C# completo para o exemplo:
using System;
using System.Collections.Generic;
namespace Estudos {
class Principal {
static void Main(string[] args) {
List<int> valores = new List<int>();
// insere valores na lista
valores.Add(4);
valores.Add(2);
valores.Add(87);
valores.Add(23);
valores.Add(100);
// agora vamos usar o laço for para percorrer os
// itens da lista
Console.WriteLine("Os itens da lista são:");
for(int i = 0; i < valores.Count; i++) {
Console.Write(valores[i] + ", ");
}
Console.WriteLine("\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Os itens da lista são: 4, 2, 87, 23, 100, |
PHP ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como ordenar um array em PHP usando a função sort() - PHP para iniciantesQuantidade de visualizações: 9119 vezes |
|
Em várias situações nós precisamos ordenar os elementos de um vetor de inteiros, de caracteres, de strings, etc. Para isso nós podemos usar a função sort() da linguagem PHP. Veja o código a seguir:
<html>
<head>
<title>Estudando PHP</title>
</head>
<body>
<?php
// um vetor com quatro elementos
$pessoas = array("Kelly", "Alice", "Mônica", "Cíntia");
// mostra os elementos sem ordenação
echo "Sem ordenar: ";
foreach($pessoas as $pessoa){
echo $pessoa . ", ";
}
// vamos ordenar o vetor em ordem alfabética
// crescente
sort($pessoas);
// mostra os elementos ordenados
echo "<br><br>Ordenados: ";
foreach($pessoas as $pessoa){
echo $pessoa . ", ";
}
?>
</body>
</html>
Ao executar este código nós teremos o seguinte resultado: Sem ordenar: Kelly, Alice, Mônica, Cíntia Ordenados: Alice, Cíntia, Kelly, Mônica Note que a função sort() requer o vetor (array) a ser ordenado e uma flag opcional indicando como a ordenação deverá ser feita. Esta flag pode ser um dos seguintes valores: SORT_REGULAR - padrão, compara os itens normalmente (não modifica o tipo). SORT_NUMERIC - compara os items numericamente. SORT_STRING - compara os itens como strings. SORT_LOCALE_STRING - compara os itens como strings, utilizando o locale atual. Utiliza o locale que pode ser modificado com setlocale(). SORT_NATURAL - compara os itens como strings utilizando "ordenação natural" tipo natsort(). SORT_FLAG_CASE - pode ser combinado (bitwise OR) com SORT_STRING ou SORT_NATURAL para ordenar strings sem considerar maiúsculas e minúsculas. |
JavaScript ::: Dicas & Truques ::: Strings e Caracteres |
Como testar se uma string termina com uma determinada substring em JavaScript usando a função endsWith()Quantidade de visualizações: 1851 vezes |
|
O método endsWith() da linguagem JavaScript foi adicionado ao objeto String na revisão ECMAScript 2015, ou ES6, também chamado de ECMAScript 6. Este método é chamado diretamente em uma variável do tipo string e retorna true se a palavra, frase ou texto terminar com uma substring específica e false em caso contrário. Veja um exemplo no qual verificamos se uma frase termina com a palavra "JavaScript":
<!doctype html>
<html>
<head>
<title>JavaScript 6</title>
</head>
<body>
<script type="text/javascript">
var frase = "Eu prefiro programar em JavaScript";
if(frase.endsWith("JavaScript")){
document.writeln("A frase termina com a palavra JavaScript");
}
else{
document.writeln("A frase não termina com a palavra JavaScript");
}
</script>
</body>
</html>
Ao executarmos este código JavaScript nós teremos o seguinte resultado: A frase termina com a palavra JavaScript É importante ter em mente que a função endsWith() diferencia letras maiúsculas de letras minúsculas. |
Nossas 20 dicas & truques de programação mais populares |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






