 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
C# ::: Dicas & Truques ::: Arquivos e Diretórios |
Como renomear ou mover arquivos em C# usando a função Move() da classe FileQuantidade de visualizações: 16599 vezes |
O método Move() da classe File é útil quando precisamos renomear ou mover arquivos. Este método recebe os caminhos e nomes antigo e novo do arquivo a ser renomeado ou movido de diretório. Veja um trecho de código no qual mostramos como renomear um arquivo texto (sem movê-lo para um diretório diferente):
static void Main(string[] args){
// não esqueça
// using System.IO;
// caminho e nome atual do arquivo
string antigo = "C:\\estudos_csharp\\arquivo.txt";
// caminho e novo nome do arquivo
string novo = "C:\\estudos_csharp\\arquivo2.txt";
// vamos renomear o arquivo
File.Move(antigo, novo);
Console.WriteLine("Arquivo renomeado com sucesso.");
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
|
VB.NET ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em VB.NET usando a função Cos() da classe Math - Calculadora de cosseno em VB.NETQuantidade de visualizações: 1323 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função Cos() da linguagem VB.NET. Esta função, que é um método da classe Math, recebe um valor numérico Double e retorna um valor Double, ou seja, também numérico) entre -1 até 1 (ambos inclusos). Veja:
Imports System
Module Program
Sub Main(args As String())
' vamos calcular o cosseno de três números
Console.WriteLine("Cosseno de 0 = " & Math.Cos(0))
Console.WriteLine("Cosseno de 1 = " & Math.Cos(1))
Console.WriteLine("Cosseno de 2 = " & Math.Cos(2))
Console.WriteLine("\nPressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código VB.NET nós teremos o seguinte resultado: Cosseno de 0 = 1 Cosseno de 1 = 0,5403023058681397 Cosseno de 2 = -0,4161468365471424 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 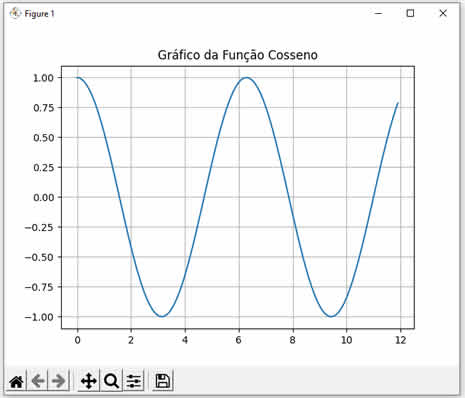 |
Java ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o seno de um número ou ângulo em Java usando o método sin() da classe MathQuantidade de visualizações: 3257 vezes |
|
Em geral, quando falamos de seno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função seno disponível nas linguagens de programação para calcular o seno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função seno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o seno é a razão entre o cateto oposto (oposto ao ângulo theta) e a hipotenusa, ou seja, o cateto oposto dividido pela hipotenusa. Veja a fórmula: \[\text{Seno} = \frac{\text{Cateto oposto}}{\text{Hipotenusa}} \] Então, se dividirmos 20 por 36.056 (na figura eu arredondei) nós teremos 0.5547, que é a razão entre o cateto oposto e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.5547. O resultado será 0.9828 (em radianos). Convertendo 0.9828 radianos para graus, nós obtemos 56.31º, que é exatamente o ângulo em graus entre o cateto oposto e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é seno na trigonometria, vamos entender mais sobre a função sin() da linguagem Java. Esta método, que faz parte da classe Math, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja:
package arquivodecodigos;
public class Estudos{
public static void main(String args[]){
System.out.println("Seno de 0 = " + Math.sin(0));
System.out.println("Seno de 1 = " + Math.sin(1));
System.out.println("Seno de 2 = " + Math.sin(2));
}
}
Ao executar este código Java nós teremos o seguinte resultado: Seno de 0 = 0.0 Seno de 1 = 0.8414709848078965 Seno de 2 = 0.9092974268256817 Note que calculamos os senos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função seno mostrada abaixo: 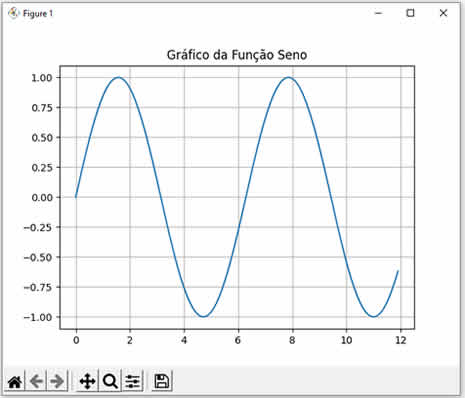 |
Java ::: Dicas & Truques ::: Matemática e Estatística |
Como calcular juros simples e composto - Calculando juros simples e montante na linguagem JavaQuantidade de visualizações: 14484 vezes |
|
O regime de juros será simples quando o percentual de juros incidir apenas sobre o valor principal. Sobre os juros gerados a cada período não incidirão novos juros. Valor Principal, ou simplesmente principal, é o valor inicial emprestado ou aplicado, antes de somarmos os juros. Transformando em fórmula temos: J = P . i . n Onde: J = juros P = principal (capital) i = taxa de juros n = número de períodos Imaginemos uma dívida de R$ 2.000,00 que deverá ser paga com juros de 5% a.m. pelo regime de juros simples e o prazo para o pagamento é de 2 meses. O cálculo em Java pode ser feito assim:
public class Estudos{
public static void main(String args[]){
double principal = 2000.00;
double taxa = 0.08;
int meses = 2;
double juros = principal * taxa * meses;
System.out.println("O total de juros a ser pago é: "
+ juros);
System.exit(0);
}
}
O montante da dívida pode ser obtido das seguintes formas: a) Montante = Principal + Juros b) Montante = Principal + (Principal x Taxa de juros x Número de períodos) M = P . (1 + (i . n)) Veja o código:
public class Estudos{
public static void main(String args[]){
double principal = 2000.00;
double taxa = 0.08;
int meses = 2;
double juros = principal * taxa * meses;
double montante = principal * (1 + (taxa * meses));
System.out.println("O total de juros a ser pago é: "
+ juros);
System.out.println("O montante a ser pago é: "
+ montante);
System.exit(0);
}
}
|
Python ::: Pandas Python Library (Biblioteca Python Pandas) ::: DataFrame |
Como retornar a quantidade de linhas em um DataFrame do Pandas usando a função len() e a propriedade indexQuantidade de visualizações: 2145 vezes |
|
Podemos tirar proveito da função len() do Python e da propriedade index do DataFrame do Pandas para contarmos as linhas do DataFrame. Lembre-se de que a propriedade index representa os rótulos das linhas. Veja o código completo para o exemplo:
# importamos a biblioteca Pandas
import pandas as pd
def main():
# vamos carregar os dados do arquivo .csv
df = pd.read_csv("C:\\estudos_python\\carros.csv",
delimiter=";")
# vamos mostrar o DataFrame resultante
print("Os dados do DataFrame são:\n")
print(df)
# agora vamos retornar a quantidade de linhas no DataFrame
quant_linhas = len(df.index)
# e mostramos o resultado
print("\nO DataFrame contém {0} linhas".format(quant_linhas))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado:
Os dados do DataFrame são:
Marca Modelo Ano Valor Vendido
0 Fiat Sienna 2010.0 23500.0 S
1 Volkswagen Polo NaN 31453.0 N
2 Volkswagen NaN 2001.0 19200.0 S
3 Fiat Palio 1995.0 7500.0 S
4 Honda Civic NaN 42000.0 S
5 Renault Sandero 2010.0 52000.0 N
6 Ford Focus 2009.0 42700.0 N
O DataFrame contém 7 linhas
|
PHP ::: Dicas & Truques ::: Arquivos e Diretórios |
Arquivos e diretórios em PHP - Como montar uma árvore de arquivos e diretórios recursivamenteQuantidade de visualizações: 16423 vezes |
|
Este exemplo mostra como listar todo o conteúdo de um diretório recursivamente em forma de árvore. Note que usei um objeto da classe RecursiveDirectoryIterator da linguagem PHP para facilitar nosso trabalho. Veja o código completo para o exemplo:
<html>
<head>
<title>Estudando PHP</title>
</head>
<body>
<?php
// nome e local do diretório
$dir = $_SERVER["DOCUMENT_ROOT"] . "/escola/app";
// função recursiva que lista o diretório atual
function montarArvore($it){
echo '<ul>';
for(; $it->valid(); $it->next()){
if($it->isDir() && !$it->isDot()) {
printf('<li>%s</li>', $it->current());
if($it->hasChildren()) {
$filho = $it->getChildren();
echo '<ul>' . montarArvore($filho) . '</ul>';
}
}
elseif($it->isFile()) {
echo '<li>'. $it->current() . '</li>';
}
}
echo '</ul>';
}
// faz a primeira chamada à função recursiva
montarArvore(new RecursiveDirectoryIterator($dir));
?>
</body>
</html>
|
Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como somar os elementos da diagonal principal de uma matriz em PythonQuantidade de visualizações: 3730 vezes |
|
A Matriz quadrada é um tipo especial de matriz que possui o mesmo número de linhas e o mesmo número de colunas, ou seja, dada uma matriz Anxm, ela será uma matriz quadrada se, e somente se, n = m, onde n é o número de linhas e m é o número de colunas. Em geral as matrizes quadradas são chamadas de Matrizes de Ordem n, onde n é o número de linhas e colunas. Dessa forma, uma matriz de ordem 4 é uma matriz que possui 4 linhas e quatro colunas. Toda matriz quadrada possui duas diagonais, e elas são muito exploradas tanto na matemática quanto na construção de algorítmos. Essas duas diagonais são chamadas de Diagonal Principal e Diagonal Secundária. A diagonal principal de uma matriz quadrada une o seu canto superior esquerdo ao canto inferior direito. Veja: 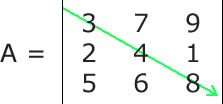 Nesta dica veremos como calcular a soma dos valores dos elementos da diagonal principal de uma matriz usando Python. Para isso, só precisamos manter em mente que a diagonal principal de uma matriz A é a coleção das entradas Aij em que i é igual a j. Assim, tudo que temos a fazer é converter essa regra para código Python. Veja um trecho de código Python completo no qual pedimos para o usuário informar os elementos da matriz e em seguida mostramos a soma dos elementos da diagonal superior:
def main():
# vamos declarar e construir uma matriz de três linhas
# e três colunas
linhas, colunas = (3, 3)
matriz = [[0 for x in range(linhas)] for y in range(colunas)]
soma_diagonal = 0 # guarda a soma dos elementos na diagonal
# principal
# vamos ler os elementos da matriz
for i in range(len(matriz)):
for j in range(len(matriz[i])):
matriz[i][j] = int(input("Informe o valor para a linha " + str(i)
+ " e coluna " + str(j) + ": "))
print()
for i in range(len(matriz)):
for j in range(len(matriz[i])):
print(matriz[i][j], end=' ')
print()
# vamos calcular a soma dos elementos da diagonal
# principal
for i in range(len(matriz)):
for j in range(len(matriz[i])):
if i == j:
soma_diagonal = soma_diagonal + matriz[i][j]
# finalmente mostramos a soma da diagonal principal
print("\nA soma dos elementos da diagonal principal é: %d" %
soma_diagonal)
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Informe o valor para a linha 0 e coluna 0: 3 Informe o valor para a linha 0 e coluna 1: 7 Informe o valor para a linha 0 e coluna 2: 9 Informe o valor para a linha 1 e coluna 0: 2 Informe o valor para a linha 1 e coluna 1: 4 Informe o valor para a linha 1 e coluna 2: 1 Informe o valor para a linha 2 e coluna 0: 5 Informe o valor para a linha 2 e coluna 1: 6 Informe o valor para a linha 2 e coluna 2: 8 3 7 9 2 4 1 5 6 8 A soma dos elementos da diagonal principal é: 15 |
Delphi ::: Dicas & Truques ::: Strings e Caracteres |
Como converter todo o conteúdo de uma string para letras minúsculas usando a função AnsiLowerCase() do DelphiQuantidade de visualizações: 12987 vezes |
Algumas vezes precisamos converter todo o conteúdo de uma string para letras minúsculas. Em Delphi isso pode ser feito com o auxílio da função AnsiLowerCase(). Esta função recebe uma string e retorna outra string com todos os caracteres minúsculos. Veja o exemplo:procedure TForm1.Button1Click(Sender: TObject); var nome: string; begin nome := 'OSMAR'; // vamos converter a string para letras minúsculas nome := AnsiLowerCase(nome); // exibe o resultado ShowMessage(nome); end; Note que esta função suporta caracteres de mais de um byte e com acentuações. Para questões de compatibilidade, esta dica foi escrita usando Delphi 2009. |
Dart ::: Dicas & Truques ::: Aplicativos e Outros |
Como calcular a distância entre dois pontos na terra em DartQuantidade de visualizações: 1705 vezes |
|
Nesta dica mostrarei como calcular a distância em quilômetros entre dois pontos na terra dadas suas latitudes e longitudes. Neste exemplo eu coloquei o valor de 6378.137 para o raio da terra, mas você pode definir para o valor que achar mais adequado. O cálculo usado neste código se baseia na Fórmula de Haversine, que determina a distância do grande círculo entre dois pontos em uma esfera, dadas suas longitudes e latitudes. Veja o código Dart completo:
// Vamos importar a biblioteca dart:io
import "dart:io";
// vamos importar a biblioteca dart:math
import "dart:math";
void main(){
// vamos ler as latitudes e longitudes das duas
// localizações
stdout.write("Informe a primeira latitude: ");
double lat1 = double.parse(stdin.readLineSync());
stdout.write("Informe a primeira longitude: ");
double lon1 = double.parse(stdin.readLineSync());
stdout.write("Informe a segunda latitude: ");
double lat2 = double.parse(stdin.readLineSync());
stdout.write("Informe a segunda longitude: ");
double lon2 = double.parse(stdin.readLineSync());
// vamos calcular a distância entre os dois pontos em Kms
double distancia = calcularDistancia(lat1, lat2, lon1, lon2);
// mostramos o resultado
print("Distância entre os dois pontos: ${distancia} kms");
}
// função que recebe dois pontos na terra e retorna a distância
// entre eles em quilômetros
double calcularDistancia(double lat1,
double lat2, double lon1, double lon2){
double raio_terra = 6378.137; // raio da terra em quilômetros
// o primeiro passo é converter as latitudes e longitudes
// para radianos
lon1 = grausParaRadianos(lon1);
lon2 = grausParaRadianos(lon2);
lat1 = grausParaRadianos(lat1);
lat2 = grausParaRadianos(lat2);
// agora aplicamos a Fórmula de Haversine
double dlon = lon2 - lon1;
double dlat = lat2 - lat1;
double a = pow(sin(dlat / 2), 2) + cos(lat1) * cos(lat2)
* pow(sin(dlon / 2),2);
double c = 2 * asin(sqrt(a));
// e retornamos a distância
return(c * raio_terra);
}
// função que permite converter graus em radianos
double grausParaRadianos(double graus){
return graus * (pi / 180);
}
Ao executar este código Dart nós teremos o seguinte resultado: Informe a primeira latitude: -16.674551 Informe a primeira longitude: -49.303598 Informe a segunda latitude: -15.579321 Informe a segunda longitude: -56.10009 A distância entre os dois pontos é: 736.9183827638687kms Neste exemplo eu calculei a distância entre as cidades de Goiânia-GO e Cuibá-MT. A latitude é a distância ao Equador medida ao longo do meridiano de Greenwich. Esta distância mede-se em graus, podendo variar entre 0o e 90o para Norte(N) ou para Sul(S). A longitude é a distância ao meridiano de Greenwich medida ao longo do Equador. |
Python ::: Dicas & Truques ::: Lista (List) |
Como contar quantas vezes um elemento aparece em uma lista do Python usando a função count()Quantidade de visualizações: 8360 vezes |
|
Em várias situações nós precisamos contar as ocorrências de um item em uma List do Python, ou seja, queremos saber quantas vezes um determinado elemento aparece na lista. Para isso nós podemos usar a função count() do objeto List. Veja um código Python completo demonstrando seu uso:
# função principal do programa
def main():
# cria uma lista de inteiros
valores = [2, 5, 12, 2, 3, 2, 17]
# vamos mostrar o conteúdo dessa lista
print("Conteúdo da lista: {0}".format(valores))
# verifica a quantidade de vezes que o
# valor 2 aparece
print("O valor 2 aparece", valores.count(2), "vezes")
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Conteúdo da lista: [2, 5, 12, 2, 3, 2, 17] O valor 2 aparece 3 vezes |
Nossas 20 dicas & truques de programação mais populares |
|
JavaScript - Cookies em JavaScript - Como escrever uma função para a criação de cookies em JavaScript |
Você também poderá gostar das dicas e truques de programação abaixo |
|
CSS - Como definir uma imagem de fundo para um botão HTML usando a propriedade background-image do CSS Java - Como calcular a transposta de uma matriz em Java - Java para Geometria Analítica e Álgebra Linear |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





