 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
PHP ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como pesquisar valores em arrays do PHP usando a função array_search()Quantidade de visualizações: 24222 vezes |
|
A função array_search() do PHP é muito útil quando precisamos pesquisar um determinado valor em um vetor e retornar o seu índice. É importante observar que esta função retorna o índice do elemento se ele for encontrado no array e, em caso contrário, retorna o valor FALSE. Veja um exemplo completo de seu uso:
<?php
$pessoas[0] = "Carlos";
$pessoas[1] = "Juliana";
$pessoas[2] = "Igor";
$pessoas[3] = "Marcelo";
$pessoas[4] = "Amélia";
$indice = array_search("Igor", $pessoas);
if($indice){
echo "O valor foi encontrado no índice " . $indice;
}
else{
echo "O valor pesquisado não foi encontrado.";
}
?>
Ao executar este código PHP nós teremos o seguinte resultado: O valor foi encontrado no índice 2. |
VisuAlg ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em VisuAlg dados dois pontos no plano cartesianoQuantidade de visualizações: 638 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem VisuAlg que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
algoritmo "Calcular o coeficiente angular de uma reta em VisuAlg"
var
// coordenadas dos dois pontos
x1, y1, x2, y2: real
// guarda o coeficiente angular
m: real
inicio
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos calcular o coeficiente angular
m <- (y2 - y1) / (x2 - x1)
// mostramos o resultado
escreva("O coeficiente angular é: ", m)
fimalgoritmo
Ao executar este código VisuAlg nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.6666666666666666 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
algoritmo "Calcular o coeficiente angular de uma reta em VisuAlg"
var
// coordenadas dos dois pontos
x1, y1, x2, y2: real
// guarda os comprimentos dos catetos oposto e adjascente
cateto_oposto, cateto_adjascente: real
// guarda o ângulo tetha (em radianos) e a tangente
tetha, tangente: real
inicio
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos obter o comprimento do cateto oposto
cateto_oposto <- y2 - y1
// e agora o cateto adjascente
cateto_adjascente <- x2 - x1
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
tetha <- ArcTan(cateto_oposto / cateto_adjascente)
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
tangente <- Tan(tetha)
// mostramos o resultado
escreva("O coeficiente angular é: ", tangente)
fimalgoritmo
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
R ::: Dicas & Truques ::: Strings e Caracteres |
Como usar a função paste() da linguagem R para concatenar strings e valores de variáveisQuantidade de visualizações: 3571 vezes |
A função paste() do R é muito útil quando precisamos unir, ou seja, concatenar um texto, frase ou palavra com um ou vários valores de variáveis. Vamos ver um exemplo? Observe o seguinte trecho de código R:
> nome <- "Osmar" [ENTER]
> idade <- 38 [ENTER]
> paste("Nome é", nome, "e idade é", idade) [ENTER]
[1] "Nome é Osmar e idade é 38"
>
Ao executar estas linhas nós teremos o seguinte resultado: Nome é Osmar e idade é 38 Note que declaramos e atribuimos às variáveis nome e idade e depois usamos a função paste() para concatenar os valores dessas duas variáveis e exibir o resultado como parte de uma frase. É importante observar que a função paste() retorna uma string. Veja este novo exemplo:
> nome <- "Osmar" [ENTER]
> idade <- 38 [ENTER]
> res <- paste("Nome é", nome, "e idade é", idade) [ENTER]
> print(res) [ENTER]
[1] "Nome é Osmar e idade é 38"
>
Note que o resultado é o mesmo. Porém, dessa vez nós guardamos o resultado da chamada à função paste() em uma variável res e depois usamos a função print() para exibir o seu conteúdo. |
Dart ::: Dicas de Estudo e Anotações ::: Estruturas de Controle |
Como usar o laço for da linguagem DartQuantidade de visualizações: 4286 vezes |
|
Em algumas situações os nossos códigos precisam executar repetidas vezes uma ou mais instruções. Para isso a linguagem Dart, assim como C, C++, Java, Python, JavaScript, Delphi, etc, nos oferece o laço for, ou loop for. Este laço é usado quando sabemos exatamente a quantidade de vezes que a instrução (ou grupo de instruções) deverá ser repetida. Veja um exemplo no qual usamos este laço para contar de 1 até 10:
void main() {
for (int i = 1; i <= 10; i++) {
print('${i}');
}
}
Ao executar este código nós teremos o seguinte resultado: 1 2 3 4 5 6 7 8 9 10 Veja que o laço for em Dart é composto de três partes: a) Inicialização da variável de controle; b) O teste de continuidade; c) O incremento ou decremento da variável de controle. Como a execução do laço se inicia no teste de continuidade, é possível termos um laço for que nunca será executado. Veja:
void main() {
for (int i = 1; i > 5; i++) {
print('${i}');
}
}
Execute este código e perceberá que nenhum valor é impresso. Isso aconteceu porque o teste condicional retornou um valor falso, impedindo até mesmo a primeira execução do laço. Veja agora um laço for que conta de 10 até 1:
void main() {
for (int i = 10; i >= 1; i--) {
print('${i}');
}
}
Para finalizar em grande estilo, veja um laço for que pede para o usuário digitar 5 idades e, em seguida, mostra a média das idades lidas:
// Vamos importar a biblioteca dart:io
import 'dart:io';
void main() {
int soma = 0;
// vamos solicitar 5 idades
for (int i = 0; i < 5; i++) {
stdout.write("Digite uma idade: ");
int idade = int.parse(stdin.readLineSync());
soma = soma + idade;
}
// Vamos mostrar a média das idades
double media = soma / 5;
print("A média das idades é $media.");
}
A execução deste código mostrará o seguinte resultado: c:\estudos_dart>dart laco_for.dart Digite uma idade: 18 Digite uma idade: 21 Digite uma idade: 34 Digite uma idade: 50 Digite uma idade: 9 A média das idades é 26.4. |
C# ::: Windows Forms ::: DataGridView |
Como retornar a quantidade de linhas em um DataGridView do C# Windows FormsQuantidade de visualizações: 14911 vezes |
A quantidade de linhas em um DataGridView do C# Windows Forms pode ser obtida por meio da propriedade RowCount. Veja:
private void button2_Click(object sender, EventArgs e){
// vamos adicionar três colunas no DataGridView
dataGridView1.Columns.Add("cidade", "Cidade");
dataGridView1.Columns.Add("estado", "Estado");
dataGridView1.Columns.Add("populacao", "População");
// vamos adicionar três linhas
dataGridView1.Rows.Add("Goiânia", "GO", "3.453,39");
dataGridView1.Rows.Add("Cuiabá", "MT", "1.876,12");
dataGridView1.Rows.Add("Curitiba", "PR", "5.346,98");
// não vamos permitir que o usuário adicione novas
// linhas (o que daria uma linha a mais na nossa
// contagem
dataGridView1.AllowUserToAddRows = false;
// vamos obter a quantidade de linhas no DataGridView
int quant_linhas = dataGridView1.RowCount;
// exibe o resultado
MessageBox.Show("O DataGridView contém " +
quant_linhas + " linhas");
}
É possível também usar a propriedade RowCount para definir a quantidade de linhas em um DataGridView: dataGridView1.RowCount = 6; Há algumas considerações importantes sobre a propriedade RowCount: 1) Se seu valor for definido como 0, todas as linhas do DataGridView serão removidas; 2) Se o novo valor for menor que o valor atual, as linhas excedentes serão removidas no final da coleção Rows; 3) Se o novo valor for maior que o valor atual, as novas linhas serão adicionadas no final da coleção Rows; 4) Se tentarmos alterar o valor desta propriedade após a definição da propriedade DataSource, uma exceção InvalidOperationException será lançada. |
C# ::: Dicas & Truques ::: Gráficos |
Como desenhar linhas em C# usando o método DrawLine() da classe Graphics - Computação Gráfica usando C#Quantidade de visualizações: 13382 vezes |
|
Uma das tarefas mais simples que realizamos quando estamos desenhando em C# é o desenho de linhas. Para isso usamos o método DrawLine() da classe Graphics. Este método recebe um objeto da classe Pen (representando a cor e espessura da caneta de desenho) e as coordenadas iniciais e finais da linha a ser desenhada. Veja um trecho de código no qual desenhamos uma linha na cor vermelha e com a espessura de dois pixels:
private void button1_Click(object sender, EventArgs e){
// vamos obter o Graphics do formulário
Graphics g = this.CreateGraphics();
// vamos desenhar uma linha na cor vermelha e com espessura
// de dois pixels
g.DrawLine(new Pen(Color.Red, 2), new Point(100, 150),
new Point(400, 450));
// vamos liberar o objeto Graphics
g.Dispose();
}
Execute este código e verá uma linha vermelha na vertical ser desenhada quando você clicar no botão. Aqui nós usamos dois objetos da classe Point. Um para as coordenadas iniciais (x = 100; y = 150) e outro para as coordenadas finais (x = 400; y = 450). É possível fornecer os valores das coordenadas diretamente. Veja: g.DrawLine(new Pen(Color.Red, 2), 100, 150, 400, 450); É possível também desenhar múltiplas linhas de uma só vez. Para isso podemos usar o método DrawLines(). Este método recebe um objeto da classe Pen e um array de objetos da classe Point representando as diversas coordenadas. Desta forma, todas as linhas serão conectadas. Veja um exemplo:
private void button1_Click(object sender, EventArgs e){
// vamos obter o Graphics do formulário
Graphics g = this.CreateGraphics();
// vamos criar várias coordenadas x e y
Point[] coordenadas = {new Point(15, 20), new Point(15, 300),
new Point(400, 300), new Point(400, 20), new Point(15, 20)};
// vamos desenhar todas as linhas conectadas usando a cor azul e a
// espessura de um pixel
g.DrawLines(new Pen(Color.Blue, 1), coordenadas);
// vamos liberar o objeto Graphics
g.Dispose();
}
Execute este código e clique no botão. Você verá um retângulo azul e com a espessura de 1 pixel ser desenhado no formulário. |
Java ::: Estruturas de Dados ::: Árvore Binária e Árvore Binária de Busca |
Como percorrer uma árvore binária em Java usando o algorítmo depth-first search (DFS) recursivoQuantidade de visualizações: 968 vezes |
|
Nesta dica mostrarei como podemos implementar o algorítmo da Busca em Profundidade (DFS, do inglês depth-first search) em Java de forma recursiva. Em outra dica desta seção que mostrei como fazer a mesma travessia de forma iterativa e usando uma pilha para backtracking (retrocesso). Antes de iniciarmos, veja a árvore binária que vamos usar no exemplo:  Note que esta árvore possui seis nós. O nó 5 é o nó raiz, e possui como filhos os nós 4 e 9. O nó 4, por sua vez, possui apenas um filho, o nó 2, ou seja, o filho da esquerda. O nó 9 possui dois filhos: o nó 3 é o filho da esquerda e o nó 12 é o filho da direita. Os filhos da árvore binária que não possuem outros filhos são chamados de folhas. Com a abordagem da busca em profundidade, começamos com o nó raiz e viajamos para baixo em uma única ramificação. Se o nó desejado for encontrado naquela ramificação, ótimo. Do contrário, continuamos subindo e pesquisando por nós não visitados. Esse tipo de busca também tem uma notação big O de O(n). Vamos à implementação? Veja o código para a classe No, que representa um nó na árvore binária:
// implementação da classe No
class No{
public int valor; // o valor do nó
public No esquerdo; // o filho da esquerda
public No direito; // o filho da direita
public No(int valor){
this.valor = valor;
this.esquerdo = null;
this.direito = null;
}
}
Veja agora o código completo para o exemplo. Note que estamos usando recursividade nesta dica. Observe também o uso de uma ArrayList para guardar os valores da árvore binária na ordem depth-first. Eis o código:
package estudos;
import java.util.ArrayList;
// implementação da classe No
class No{
public int valor; // o valor do nó
public No esquerdo; // o filho da esquerda
public No direito; // o filho da direita
public No(int valor){
this.valor = valor;
this.esquerdo = null;
this.direito = null;
}
}
public class Estudos{
public static void main(String[] args){
// vamos criar os nós da árvore
No cinco = new No(5); // será a raiz da árvore
No quatro = new No(4);
No nove = new No(9);
No dois = new No(2);
No tres = new No(3);
No doze = new No(12);
// vamos fazer a ligação entre os nós
cinco.esquerdo = quatro;
cinco.direito = nove;
quatro.esquerdo = dois;
nove.esquerdo = tres;
nove.direito = doze;
// agora já podemos efetuar o percurso depth-first
ArrayList<Integer> valores = new ArrayList<>();
percursoDepthFirst(valores, cinco);
System.out.println("Os valores na ordem Depth-First são: " + valores);
}
public static void percursoDepthFirst(ArrayList<Integer> valores, No no){
if(no != null){
// vamos adicionar o valor deste nó no ArrayList
valores.add(no.valor);
// passamos para o filho esquerdo
percursoDepthFirst(valores, no.esquerdo);
// passamos para o filho direito
percursoDepthFirst(valores, no.direito);
}
}
}
Ao executarmos este código Java nós teremos o seguinte resultado: Os valores na ordem Depth-First são: [5, 4, 2, 9, 3, 12] Compare estes valores com a imagem vista anteriormente para entender ainda melhor o percurso ou busca Depth-First. |
Java ::: Coleções (Collections) ::: Set (Conjunto) |
Como usar objetos da interface Set para representar a união de dois ou mais conjuntos na linguagem JavaQuantidade de visualizações: 4686 vezes |
|
Na teoria dos conjuntos, a união de dois ou mais conjuntos é o conjunto dos elementos que pertencem a pelo menos um destes conjuntos. Assim, seja A = {2, 5, 8, 19, 30} e B = {2, 3, 1, 30}. A união desses dois conjuntos é C = {1, 2, 3, 5, 8, 19, 30}. Na programação Java podemos representar a união de dois conjuntos usando objetos da interface Set e qualquer uma de suas implementações. Para este exemplo vou usar a classe TreeSet, que permite a ordenação dos elementos. Veja o código:
package estudos;
import java.util.Iterator;
import java.util.Set;
import java.util.TreeSet;
public class Estudos{
public static void main(String[] args) {
// primeiro conjunto
Set<Integer> conjuntoA = new TreeSet<>();
conjuntoA.add(2);
conjuntoA.add(5);
conjuntoA.add(8);
conjuntoA.add(19);
conjuntoA.add(30);
// segundo conjunto
Set<Integer> conjuntoB = new TreeSet<>();
conjuntoB.add(2);
conjuntoB.add(3);
conjuntoB.add(1);
conjuntoB.add(30);
// vamos obter a união dos dois conjuntos
Set<Integer> conjuntoC = uniao(conjuntoA, conjuntoB);
// vamos exibir os elementos no conjunto C
Iterator iterator = conjuntoC.iterator();
while(iterator.hasNext()){
System.out.println(iterator.next());
}
}
// método genérico que permite obter a união de dois conjuntos
public static <T> Set<T> uniao(Set<T> conjA, Set<T> conjB){
// Primeiro o conjunto C recebe todos os elementos do conjunto A
Set<T> conjC = new TreeSet<>(conjA);
// Em seguida o conjunto C recebe todos os elementos do conjunto B.
// Como um Set não aceita elementos duplicados, apenas os elementos
// de B que ainda não estejam no conjunto C serão aceitos
conjC.addAll(conjB);
return conjC;
}
}
Ao executarmos este código teremos o seguinte resultado: 1 2 3 5 8 19 30 |
C# ::: Desafios e Lista de Exercícios Resolvidos ::: Matemática e Estatística |
Exercícios Resolvidos de C# - Como calcular juros simples em C# - Um programa C# que lê o valor principal, o tempoQuantidade de visualizações: 733 vezes |
|
Pergunta/Tarefa: Saber como escrever um programa C# que recebe o valor principal, o tempo e a taxa de juros e retorna os juros simples a serem pagos ou recebidos é uma habilidade que todo programador deve aprender em algum ponto de sua carreira. Sendo assim, escreva um algoritmo em C# que pede para o usuário informar um valor a ser pago ou recebido, o tempo em dias, meses ou anos e a taxa de juros (sem dividi-la por 100) e retorne os juros simples a serem pagos ou recebidos. Note que, se você quiser mostrar o valor total a ser pago ou recebido, basta somar os juros ao valor principal. Antes, porém, veja a fórmula do cálculo de juros simples: \[\text{Juros} = \frac{\text{C} \times \text{i} \times \text{t}}{100}\] Onde: C é o valor a ser pago ou a ser recebido; i é a taxa de juros (sem dividir por 100); t é o tempo em dias, meses, anos, etc. Sua saída deverá ser parecida com: Informe o valor principal: 600 Taxa de juros: 12 Informe o tempo: 5 Juros a serem pagos ou recebidos: 360.0 Veja a resolução comentada deste exercício usando C#:
using System;
namespace Estudos {
class Principal {
// função principal do programa C#
static void Main(string[] args) {
// vamos ler o valor principal
Console.Write("Informe o valor principal: ");
double principal = Double.Parse(Console.ReadLine());
// agora vamos ler a taxa de juros
Console.Write("Taxa de juros: ");
double taxa = Double.Parse(Console.ReadLine());
// finalmente o tempo em dias, meses, anos, etc
Console.Write("Informe o tempo: ");
int tempo = Int32.Parse(Console.ReadLine());
// vamos calcular os juros
double juros = (principal * taxa * tempo) / 100;
// e mostramos o resultado
Console.WriteLine("Juros a serem pagos ou recebidos: " + juros);
Console.WriteLine("\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
|
C ::: Dicas & Truques ::: Matemática e Estatística |
Como elevar uma base a um determinado expoente usando a função pow() da linguagem CQuantidade de visualizações: 3406 vezes |
Em algumas situações nós precisamos efetuar cálculos de potenciação em C, ou seja, elevar um número (uma base) a um determinado expoente e obter sua potência. Veja a figura a seguir: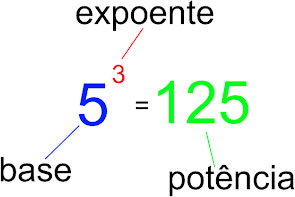 Veja que aqui o valor 5 foi elevado ao cubo, ou seja, ao expoente 3 e obtemos como resultado sua potência: 125. A linguagem C nos fornece a função pow(), presente no header math.h que recebe como argumentos a base e o expoente e nos retorna a potência (como um valor double). Veja um exemplo de seu uso no código abaixo:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
int base = 4;
int expoente = 5;
double potencia = pow(4, 5);
printf("A base %d elevada ao expoente %d é igual à potência %f\n\n",
base, expoente, potencia);
system("PAUSE");
return 0;
}
Ao executarmos este código C nós teremos o seguinte resultado: A base 4 elevada ao expoente 5 é igual à potência 1024.000000 Note que a função pow() da linguagem C retorna um valor double. |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Java - Como percorrer uma árvore binária em Java usando o algorítmo depth-first search (DFS) recursivo Java - Como converter Coordenadas Cartesianas para Coordenadas Polares usando Java - Java para Engenharia JavaScript - Como retornar o tamanho de uma string em JavaScript usando a propriedade length do objeto String |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




