 |
|||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
|
|||||
JavaScript ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o comprimento da hipotenusa em JavaScript dadas as medidas do cateto oposto e do cateto adjascenteQuantidade de visualizações: 954 vezes |
Nesta dica mostrarei como é possível usar a linguagem JavaScript para retornar o comprimento da hipotenusa dadas as medidas do cateto oposto e do cateto adjascente. Vamos começar analisando a imagem a seguir: Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras): \[c^2 = a^2 + b^2\] Tudo que temos a fazer a converter esta fórmula para código JavaScript. Veja:
<html>
<head>
<title>Estudos JavaScript</title>
</head>
<body>
<script type="text/javascript">
var a = 20; // medida do cateto oposto
var b = 30; // medida do cateto adjascente
// agora vamos calcular o comprimento da hipotenusa
var c = Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2));
// e mostramos o resultado
document.writeln("O comprimento da hipotenusa é: " + c);
</script>
</body>
</html>
Ao executar este código JavaScript nós teremos o seguinte resultado: O comprimento da hipotenusa é: 36.05551275463989 Como podemos ver, o resultado retornado com o código JavaScript confere com os valores da imagem apresentada. |
Delphi ::: Dicas & Truques ::: Ponteiros, Referências e Memória |
Como usar nil para testar ou indicar que um ponteiro Delphi não referencia nenhuma posição de memóriaQuantidade de visualizações: 15221 vezes |
O propósito dos ponteiros é nos permitir acessar e manipular os valores de outras variáveis. Isso é feito acessando-se diretamente o endereço de memória destas variáveis. Porém, há situações nas quais queremos testar se um determinado ponteiro está realmente apontando para um local na memória. Veja o seguinte trecho de código:procedure TForm1.Button1Click(Sender: TObject); var pvalor: ^integer; begin // vamos exibir o valor da variável referenciada pelo // ponteiro pvalor ShowMessage(IntToStr(pvalor^)); end; Ao executarmos este código nós teremos um valor aleatório sendo exibido (e um warning do tipo W1036 Variable 'pvalor' might not have been initialized. Isso acontece porque criamos um ponteiro para um Integer mas não indicamos o endereço da variável para a qual ele aponta, ou seja, até o momento este ponteiro é nulo (não aponta para nenhuma posição de memória). Mova a declaração do ponteiro para a seção interface e verá que código compilará mas teremos uma exceção do tipo EAccessViolation (Exception class EAccessViolation with message 'Access violation at address ... in module ...). Clássico erro de lógica. Estamos tentando acessar dados não existentes na memória. Esta situação pode ser evitada testando se o ponteiro ainda é nulo antes de tentarmos desreferenciá-lo. Veja:
procedure TForm1.Button1Click(Sender: TObject);
begin
// vamos exibir o valor da variável referenciada pelo
// ponteiro pvalor
if pvalor = nil then
ShowMessage('O ponteiro ainda é nulo.')
else
ShowMessage(IntToStr(pvalor^));
end;
Note que movi a declaração do ponteiro para a secão interface, de forma a torná-la global. Isso evita que o ponteiro seja automaticamente inicializado (o que sempre acontece com as variáveis locais). Ao executar o código novamente você verá a mensagem indicando que o ponteiro ainda é nulo. Podemos também usar nil para, explicitamente, marcar um ponteiro como nulo, ou seja, definir que o ponteiro não aponta para nenhum local na memória. Comece declarando as variáveis abaixo na seção interface do formulário: valor: Integer; pvalor: ^Integer; Em seguida coloque o código abaixo no evento Click de um botão: procedure TForm1.Button1Click(Sender: TObject); begin // vamos atribuir um valor à variável valor valor := 14; // vamos "apontar" nosso ponteiro para o local de // memória da variável valor pvalor := @valor; // vamos exibir o valor da variável apontada por pvalor ShowMessage(IntToStr(pvalor^)); // vamos marcar pvalor como nulo pvalor := nil; // vamos causar um EAccessViolation já que pvalor // não aponta para nenhum local na memória agora ShowMessage(IntToStr(pvalor^)); end; Sempre que marcamos um ponteiro como nil, a memória até então ocupada por ele é liberada para uso por parte do sistema operacional ou demais programas. Este procedimento ajuda a evitar os vazamentos de memória (memory leak) tão frequentes em códigos que trabalham com memória alocada dinamicamente. Para fins de compatibilidade, esta dica foi escrita usando Delphi 2009. |
Delphi ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cateto oposto dadas as medidas da hipotenusa e do cateto adjascente em DelphiQuantidade de visualizações: 2869 vezes |
|
Todos estamos acostumados com o Teorema de Pitágoras, que diz que "o quadrado da hipotenusa é igual à soma dos quadrados dos catetos". Baseado nessa informação, fica fácil retornar a medida do cateto oposto quando temos as medidas da hipotenusa e do cateto adjascente. Isso, claro, via programação em linguagem Delphi. Comece observando a imagem a seguir:  Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. A medida da hipotenusa é, sem arredondamentos, 36.056 metros. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras): \[c^2 = a^2 + b^2\] Tudo que temos que fazer é mudar a fórmula para: \[a^2 = c^2 - b^2\] Veja que agora o quadrado do cateto oposto é igual ao quadrado da hipotenusa menos o quadrado do cateto adjascente. Não se esqueça de que a hipotenusa é o maior lado do triângulo retângulo. Veja agora como esse cálculo é feito em linguagem Delphi:
procedure TForm2.Button1Click(Sender: TObject);
var
a, b, c: Real;
begin
c := 36.056; // medida da hipotenusa
b := 30; // medida do cateto adjascente
// agora vamos calcular o comprimento da cateto oposto
a := sqrt(sqr(c) - sqr(b));
// e mostramos o resultado
Edit1.Text := 'A medida do cateto oposto é: ' +
FloatToStr(a);
end;
Veja que o cálculo é feito a partir do evento Click de um botão Button1 e o resultado é apresentado na propriedade Text de uma caixa de texto Edit1. Ao executar este código Delphi nós teremos o seguinte resultado: A medida do cateto oposto é: 20,0008783807112 Como podemos ver, o resultado retornado com o código Delphi confere com os valores da imagem apresentada. |
C# ::: Dicas & Truques ::: Matemática e Estatística |
Como testar se um número é primo em C#Quantidade de visualizações: 7852 vezes |
|
O Número Primo é o número maior que 1 e que só pode ser dividido por 1 e por ele mesmo, ou seja, números primos não podem ser divididos por outros números, a não ser por ele mesmo e pelo número 1. Dessa forma, 2, 3, 5, 7, 11, 13, 17, etc, são todos números primos. É importante observar que 0 e 1 não são números primos, e que o número 2 é o único número primo par. Veja agora um código C# completo que pede para o usuário informar um número inteiro positivo e mostra uma mensagem indicando se o número informado é primo ou não:
using System;
namespace Estudos {
class Program {
static void Main(string[] args) {
bool primo = true;
// vamos solicitar um número inteiro positivo
Console.Write("Informe um número inteiro positivo: ");
int numero = int.Parse(Console.ReadLine());
// o número é negativo?
if (numero < 0) {
Console.WriteLine("Número inválido.");
}
// é 0 ou 1?
else if ((numero == 0) || (numero == 1)) {
Console.WriteLine("Número válido, mas não é primo.");
}
// passou até aqui. Vamos testar se o número é primo
else {
for (int i = 2; i <= (numero / 2); i++) {
// se passar no teste, não é primo
if (numero % i == 0) {
primo = false; // recebe false
break;
}
}
if (primo) {
Console.WriteLine("O número informado é primo");
}
else {
Console.WriteLine("O número informado não é primo");
}
}
Console.WriteLine("\n\nPressione qualquer tecla para sair...");
// pausa o programa
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Informe um número inteiro positivo: 9 O número informado não é primo |
Java ::: Pacote java.lang ::: String |
Java Avançado - Como usar o método getBytes() da classe String para obter uma sequência de valores do tipo byteQuantidade de visualizações: 8642 vezes |
Em algumas situações gostaríamos de obter os caracteres de uma string como uma representação de inteiros em bytes. Para isso podemos usar o método getBytes(). Veja sua assinatura:public byte[] getBytes()
public class Main {
public static void main(String[] args) {
// vamos declarar um objeto da classe String
String palavra = "Arquivo";
// vamos obter os bytes usados na palavra anterior
byte bytes[] = palavra.getBytes();
// vamos percorrer a matriz de bytes e mostrá-los individualmente
for(int i = 0; i < bytes.length; i++){
System.out.print(bytes[i] + " ");
}
}
}
Ao executarmos este código teremos o seguinte resultado: 65 114 113 117 105 118 111 De fato, o valor 65 é o código inteiro para o caractere "A". É importante observar que alguns caracteres não cabem em um byte (que possui o valor 127 como maior valor inteiro). Isso resulta na conversão para valores negativos. Há outras duas sobrecargas do método getBytes() da classe String. A primeira: byte[] getBytes(Charset charset) byte[] getBytes(String charsetName) |
Python ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Como usar o laço for do Python - Apostila Python para iniciantes - O laço forQuantidade de visualizações: 12951 vezes |
|
O laço for (laço para) em Python é um pouco diferente daquele encontrado em Java, C ou C++. Na verdade, o laço for da Python está mais para o laço foreach do C# e o novo laço for do Java 1.5. Em Python, o laço for funciona com sequencias (range), ou seja, a cada iteração do laço, um elemento da sequencia é retornado. Vamos ver isso mais de perto. Veja o exemplo a seguir:
def main():
for i in range(1, 11):
print(i)
if __name__== "__main__":
main()
Este trecho de código exibirá os números de 1 até 10. Veja que o último limite não é incluído na contagem. Este exemplo pode também ser escrito assim:
def main():
for i in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]:
print(i)
if __name__== "__main__":
main()
|
C# ::: Desafios e Lista de Exercícios Resolvidos ::: C# Básico |
Exercício Resolvido de C# - Como ler um número inteiro e imprimir seu sucessor e seu antecessor em C#Quantidade de visualizações: 1116 vezes |
|
Pergunta/Tarefa: Escreva um programa C# para ler um número inteiro e imprimir seu sucessor e seu antecessor. O usuário poderá informar um valor positivo ou negativo. Sua saída deverá ser parecida com: Informe um número inteiro: 16 O número informado foi: 16 O antecessor é 15 O sucessor é: 17 Veja a resolução comentada deste exercício usando C#:
using System;
namespace Estudos {
class Principal {
static void Main(string[] args) {
// vamos pedir ao usuário que informe um número inteiro
Console.Write("Informe um número inteiro: ");
int numero = Int32.Parse(Console.ReadLine());
// vamos calcular o sucessor do número informado
int sucessor = numero + 1;
// vamos calcular o antecessor do número informado
int antecessor = numero - 1;
// e agora mostramos os resultados
Console.WriteLine("O número informado foi: {0}", numero);
Console.WriteLine("O antecessor é {0}", antecessor);
Console.WriteLine("O sucessor é: {0}", sucessor);
Console.WriteLine("\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
|
Java ::: Java para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular o determinante de uma matriz 3x3 usando a regra de Sarrus em Java - Java para Álgebra LinearQuantidade de visualizações: 3782 vezes |
|
Como calcular o determinante de uma matriz 3x3 usando a Regra de Sarrus em Java - Java para Álgebra Linear Os estudos da Geometria Analítica e Álgebra Linear envolvem, em boa parte de seus cálculos, a magnitude de vetores, ou seja, o módulo, tamanho, comprimento ou intensidade dos vetores. E isso não é diferente em relação às matrizes. Quando uma matriz é envolvida nos cálculos, com muita frequência precisamos obter o seu determinante, que nada mais é que um número real associado à todas as matrizes quadradas. Nesta dica mostrarei como obter o determinante de uma matriz quadrada de ordem 3, ou seja, três linhas e três colunas, usando a regra de Sarrus (somente matrizes 3x3). Note que é possível obter o mesmo resultado com o Teorema de Laplace, que não está restrito às matrizes quadradas de ordem 3. Veja também que não considerei as propriedades do determinante, o que, em alguns casos, simplifica muito os cálculos. Então, vamos supor a seguinte matriz 3x3: 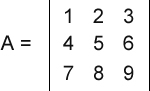 O primeiro passo é copiarmos a primeira e a segunda colunas para o lado direito da matriz. Assim: 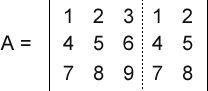 Agora dividimos a matriz em dois conjuntos: três linhas diagonais descendentes e três linhas diagonais ascendentes: 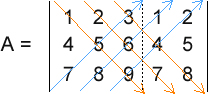 Agora é só efetuar cálculos. Multiplicamos e somamos os elementos de cada conjunto, subtraindo o segundo conjunto do primeiro. Veja: (1 x 5 x 9 + 2 x 6 x 7 + 3 x 4 x 8) - (7 x 5 x 3 + 8 x 6 x 1 + 9 x 4 x 2) = 0 Como podemos ver, o determinante dessa matriz é 0. E agora veja o código Java no qual declaramos e instanciamos uma matriz 3x3 de double e, em seguida, calculamos o seu determinante:
package arquivodecodigos;
public class Estudos{
public static void main(String[] args){
double m[][] = {{1, 2, 3}, {2, 5, 2}, {1, 3, 1}};
// calcula o determinante usando a Regra de Sarrus
double det = ((m[0][0] * m[1][1] * m[2][2]) + (m[0][1]
* m[1][2] * m[2][0]) + (m[0][2] * m[1][0] * m[2][1]))
- ((m[2][0] * m[1][1] * m[0][2]) + (m[2][1]
* m[1][2] * m[0][0]) + (m[2][2] * m[1][0] * m[0][1]));
System.out.println("O determinante da matriz é: " + det);
}
}
Ao executar este código Java nós teremos o seguinte resultado: O determinante da matriz é: 2.0 |
Delphi ::: dbExpress ::: TSQLDataSet |
Como obter a quantidade de campos nos registros retornados em um TSQLDataSet do Delphi usando a propriedade FieldCountQuantidade de visualizações: 11076 vezes |
|
Em algumas situações precisamos saber a quantidade de campos retornados em um objeto TSQLDataSet depois de dispararmos o comando SQL SELECT definido em sua propriedade CommandText. Para isso podemos usar a propriedade FieldCount. Veja sua assinatura: property FieldCount: Integer; Esta propriedade é definida originalmente em TDataSet e herdada pela classe TSQLDataSet. Veja um trecho de código no qual disparamos um comando SQL SELECT em uma tabela contatos e exibimos a quantidade de campos dos registros retornados:
procedure TForm3.Button1Click(Sender: TObject);
begin
// vamos definir o comando SQL a ser executado
SQLDataSet1.CommandText := 'SELECT * FROM contatos';
// vamos executar o comando
SQLDataSet1.Open;
// vamos obter a quantidade de registros retornados
ShowMessage('Quantidade de campos retornados: ' +
IntToStr(SQLDataSet1.FieldCount));
end;
Ao executarmos este trecho de código teremos uma mensagem com o seguinte texto: Quantidade de campos retornados: 5. Note que a propriedade FieldCount inclui somente os campos listados na propriedade Fields. Quaisquer campos agregados listados pela propriedade AggFields não são incluídos na contagem. |
C ::: Desafios e Lista de Exercícios Resolvidos ::: C Básico |
Exercícios Resolvidos de C - Como testar se um número é potência de dois usando CQuantidade de visualizações: 685 vezes |
|
Pergunta/Tarefa: Escreva um programa C contendo um método que recebe um número inteiro e retorna um valor boolean indicando se o valor informado é potência de dois. Sua saída deverá ser parecida com: Informe um valor inteiro: 8 O valor 8 é potência de dois Informe um valor inteiro: 34 O valor 34 não é potência de dois Informe um valor inteiro: 64 O valor 64 é potência de dois Veja a resolução comentada deste exercício usando C:
#include <stdio.h>
#include <stdlib.h>
#include <locale.h>
// função que recebe um número inteiro e informe se ele é
// potência de dois
int is_potencia_dois(int n){
// usamos o operador AND de bits para verificar se n AND n-1
// é igual a 0
return (n > 0) && (n & (n - 1)) == 0;
}
int main(int argc, char *argv[]){
// variáveis usadas para
int valor;
setlocale(LC_ALL,""); // para acentos do português
// vamos pedir para o usuário informar um valor inteiro
printf("Informe um valor inteiro: ");
scanf("%d", &valor);
// vamos testar se o número informado é potência de dois
if(is_potencia_dois(valor)){
printf("O valor %d é potência de dois", valor);
}
else{
printf("O valor %d não é potência de dois", valor);
}
printf("\n\n");
system("PAUSE");
return 0;
}
|
Nossas 20 dicas & truques de programação mais populares |
|
Python - Como exibir os valores de 0 a 10 em ordem decrescente usando o laço for da linguagem Python |
Você também poderá gostar das dicas e truques de programação abaixo |
|
JavaScript - Como calcular o comprimento da hipotenusa em JavaScript dadas as medidas do cateto oposto e do cateto adjascente Ruby - Exercício Resolvido de Ruby - Como percorrer os elementos de um array em Ruby usando a função each |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




