 |
|||||
|
|||||
C++ ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de C++ - Desafio do número ausente. Dado um vetor de números naturais 1..n, encontre o valor ausenteQuantidade de visualizações: 709 vezes |
|
Pergunta/Tarefa: Dado o vetor:
int valores[] = {1, 8, 7, 2, 6, 5, 3};
Encontre o elemento ausente na sequência de valores do vetor, sabendo que o primeiro valor é 1 e o último elemento é 8. Perceba que o vetor não precisa estar ordenado. Além disso, o entrevistador se certificará de que os valores serão sempre positivos e não haverá valores repetidos. Sua saída deverá ser parecida com: O número ausente é: 4 Dica: Use a fórmula n * (n + 1) / 2 para facilitar a resolução do exercício. Veja a resolução comentada deste exercício usando C++:
#include <string>
#include <iostream>
using namespace std;
int main(int argc, char *argv[]){
// vamos declarar um vetor de inteiros faltando
// um valor na sequência (não necessariamente ordenada)
// Note a ausência do número 4
int valores[] = {1, 8, 7, 2, 6, 5, 3};
int i, soma_n, ausente, soma_elementos;
int quant = 8; // tamanho do vetor + 1
// o primeiro passo é obter a soma de 1..n elementos
// natuais usando a fórmula n*(n+1)/2
soma_n = (quant * (quant + 1)) / 2;
// agora vamos somar os elementos do vetor
soma_elementos = 0;
for(i = 0; i < 7; i++){
soma_elementos = soma_elementos + valores[i];
}
// agora calculamos o valor ausente
ausente = soma_n - soma_elementos;
// vamos mostrar o resultado
cout << "O número ausente é: " << ausente << endl;
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
|
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Sistemas Digitais - Manipulação de Bits |
Exercícios Resolvidos de Java - Como fazer o complemento de 1 de um número binário em Java - Solução usando manipulação de stringsQuantidade de visualizações: 469 vezes |
|
Pergunta/Tarefa: Em Sistemas Digitais e na manipulação de bits, o complemento de 1 de um número binário é realizado de forma direta invertendo-se os "0s" e "1s", ou seja, todo zero (0) vira um (1) e todo um (1) vira zero (0). Dessa forma, se tivermos o número binário 11001, seu complemento de 1 será 00110. Escreva um programa Java que pede para o usuário informar um número binário e exiba o seu complemento de um. Para esta solução você deverá usar exclusivamente manipulação de strings. Sua saída deve ser parecida com: Informe um número binário: 1011001 O complemento de 1 é: 0100110 Veja a resolução comentada deste exercício usando Java:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// vamos solicitar um número binário
System.out.print("Informe um número binário: ");
String binario = entrada.nextLine();
// vamos converter a string em um arrays de chars
char digitos[] = binario.toCharArray();
// agora percorremos todos os dígitos do número binário
// e trocamos os "0s" por "1s" e vice-versa
for(int i = 0; i < digitos.length; i++){
if(digitos[i] == '0'){
digitos[i] = '1';
}
else{
digitos[i] = '0';
}
}
// convertemos de novo para string
String complemento1 = String.valueOf(digitos);
// e mostramos o resultado
System.out.println("O complemento de 1 é: " + complemento1);
}
}
|
Java ::: Dicas & Truques ::: Data e Hora |
Como adicionar ou subtrair horas à data atual usando o método add() e a constante Calendar.HOUR da classe Calendar do JavaQuantidade de visualizações: 554 vezes |
Nesta dica mostrarei como podemos usar a função add() e a constante Calendar.HOUR da classe Calendar do Java para adicionar ou subtrair horas de uma data. Veja o exemplo a seguir:
package estudos;
import java.util.Calendar;
public class Estudos {
public static void main(String[] args) {
// vamos construir uma instância da classe Calendar
Calendar agora = Calendar.getInstance();
// vamos exibir a data e hora atuais
System.out.println("Data e hora atual: " +
agora.getTime().toString());
// adiciona 15 hora à hora atual
agora.add(Calendar.HOUR, 13);
// mostra a data e hora com as 15 horas adicionadas
System.out.println("Daqui a 15 horas: " +
agora.getTime().toString());
}
}
Ao executar este código Java nós teremos o seguinte resultado: Data e hora atual: Mon Jan 16 12:33:26 BRST 2023 Daqui a 15 horas: Tue Jan 17 01:33:26 BRST 2023 Se quisermos subtrair as horas ao invés de adicionar, basta fornecermos um valor negativo para o método add(). |
Android Java ::: android.widget ::: Button |
Como detectar um clique em um botão do Android usando o evento onClick no XML de layoutQuantidade de visualizações: 2303 vezes |
|
Nesta dica mostrarei como podemos detectar um clique em um botão usando o evento onClick diretamente no arquivo XML de layout. No entanto, para usar este artifício, algumas regras devem ser seguidas: a) O método chamado pelo clique do botão deverá ser public e retornar void; b) O único parâmetro do método deverá conter apenas um objeto da classe View, representando a view na qual o evento onclick ocorreu. Veja um exemplo completo no qual detectamos o clique no botão e exibimos uma mensagem AlertDialog contendo apenas um botão OK. Comece analisando o XML de layout (o nome do botão foi definido no arquivo strings.xml):
<?xml version="1.0" encoding="utf-8"?>
<LinearLayout xmlns:android="
http://schemas.android.com/apk/res/android"
android:orientation="vertical"
android:layout_width="fill_parent"
android:layout_height="fill_parent">
tools:context=".MainActivity">
<Button xmlns:android="
http://schemas.android.com/apk/res/android"
android:id="@+id/button_send"
android:layout_width="wrap_content"
android:layout_height="wrap_content"
android:text="@string/btn_enviar"
android:onClick="enviarMensagem"
/>
</LinearLayout>
Veja agora o código Java no MainActivity.java:
package com.example.estudosandroid;
import androidx.appcompat.app.AppCompatActivity;
import android.content.DialogInterface;
import android.os.Bundle;
import android.view.View;
import android.app.AlertDialog;
public class MainActivity extends AppCompatActivity {
@Override
protected void onCreate(Bundle savedInstanceState) {
super.onCreate(savedInstanceState);
setContentView(R.layout.activity_main);
}
// método público que será chamado ao clicarmos no botão
public void enviarMensagem(View view) {
AlertDialog dialogo = new
AlertDialog.Builder(MainActivity.this).create();
dialogo.setTitle("Aviso");
dialogo.setMessage("Esta é uma mensagem de aviso");
dialogo.setButton(AlertDialog.BUTTON_NEUTRAL, "OK",
new DialogInterface.OnClickListener() {
public void onClick(DialogInterface dialog,
int which){
dialog.dismiss(); // fecha o AlertDialog
}
}
);
dialogo.show();
}
}
|
Python ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a apótema de um polígono regular de N lados em PythonQuantidade de visualizações: 737 vezes |
|
Uma das formas mais comuns de se obter a área de um polígono regular é usando a seguinte fórmula: \[\text{A} = \frac{1}{2} \cdot \text{p} \cdot \text{a} \] Onde: p = Perímetro, ou seja, a soma dos comprimentos de todos os lados. a = Apótema, isto é, uma parte que une o centro do polígono ao meio de qualquer lado que esteja perpendicular. Agora que já estamos alinhados, saiba que calcular a apótema de um polígono regular "na mão" é fácil, já que só precisamos medir a distância de dois lados opostos e dividir por dois ou traçar linhas cruzadas e medir a distância de um dos lados até a interseção dessas linhas. No entanto, em programação a coisa já é um pouco mais complicada. Nesta dica mostrarei como podemos realizar esta tarefa em Python. Para isso usaremos alguns truques de trigonometria. Comece analisando a seguinte imagem: 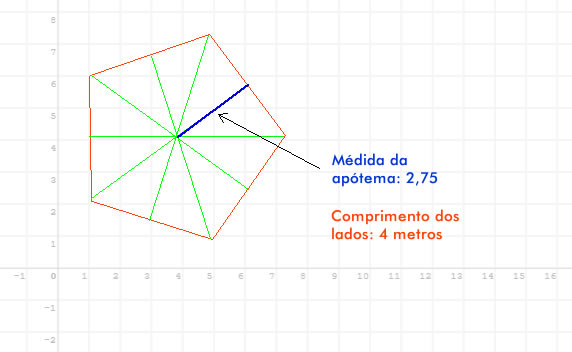 Note que temos um pentágono com cada lado medindo 4 metros. Recorde que um pentágono é um polígono regular de 5 lados. Para deixar a dica mais didática eu coloquei também uma linha azul representando a apótema do polígono e as linhas cruzadas. Veja agora o código Python que recebe a quantidade de lados do polígono, o comprimento dos lados e retorna a apótema:
# vamos importar o módulo Math
import math
# função que calcula e retorna a apótema de um
# polítono regular
def calcular_apotema(lados, comprimento):
# a quantidade de lados e o comprimento deles
# não podem ser negativos
if lados < 0 or comprimento < 0:
return -1
# calculamos a apótema
return (comprimento / (2 * math.tan((180 / lados)
* math.pi / 180)))
# função principal do programa
def main():
# vamos ler a quantidade de lados
lados = int(input("Informe a quantidade de lados: "))
# vamos ler o comprimento dos lados
comprimento = int(input("Informe o comprimento dos lados: "))
# e agora calculamos a apótema dos polígono
apotema = calcular_apotema(lados, comprimento)
# e mostramos o resultado
print("A apótema do polígono é: {0}".format(apotema))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Informe a quantidade de lados: 5 Informe o comprimento dos lados: 4 A apótema do polígono é: 2.7527638409423476 |
JavaFX ::: Pacote javafx.scene.layout (Package javafx.scene.layout) ::: HBox (Classe HBox) |
Como definir o espaço interno do HBox do JavaFX usando o método setPadding()Quantidade de visualizações: 961 vezes |
|
Em algumas situações nós precisamos definir o espaço interno, ou seja, o padding, do gerenciador de layout HBox. Para isso nós podemos usar o método setPadding() e fornecer a ele um objeto da classe javafx.geometry.Insets. Este método é herdado da classe javafx.scene.layout.Region. Lembre-se de que a função setPadding() define o espaço interno do VBox, ou seja, o espaço que deverá existir entre suas margens e os componentes contidos nele. Veja um trecho de código JavaFX no qual temos um gerenciador de layout HBox e três botões:
package estudosjavafx;
import javafx.application.Application;
import javafx.geometry.Insets;
import javafx.scene.Scene;
import javafx.scene.control.Button;
import javafx.scene.layout.HBox;
import javafx.stage.Stage;
public class EstudosJavaFX extends Application {
public static void main(String[] args){
launch(args);
}
@Override
public void start(Stage primaryStage){
// vamos criar três botões
Button btn1 = new Button("Botão 1");
Button btn2 = new Button("Botão 2");
Button btn3 = new Button("Botão 3");
// agora criamos um laytou HBox e colocamos
// os três botões nele
HBox hBox = new HBox();
hBox.getChildren().add(btn1);
hBox.getChildren().add(btn2);
hBox.getChildren().add(btn3);
// vamos definir o espaço interno do HBox usando
// um Inserts (top, direita, baixo, esquerda)
hBox.setPadding(new Insets(20, 20, 20, 20));
// criamos a cena e fornecemos o layout a ela
// e definimos a largura e altura da cena
Scene scene = new Scene(hBox, 400, 300);
// adicionamos a cena ao palco principal
primaryStage.setScene(scene);
// e mostramos o palco
primaryStage.show();
}
}
Execute este código, experimente alterar os valores do objeto Insets fornecido ao método setPadding e veja os resultados obtidos. |
VB.NET ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em VB.NET dados dois pontos no plano cartesianoQuantidade de visualizações: 1164 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem VB.NET que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
Imports System
Module Program
Sub Main(args As String())
' x e y do primeiro ponto
Console.Write("Informe a coordenada x do primeiro ponto: ")
Dim x1 As Double = Double.Parse(Console.ReadLine())
Console.Write("Informe a coordenada y do primeiro ponto: ")
Dim y1 As Double = Double.Parse(Console.ReadLine())
' x e y do segundo ponto
Console.Write("Informe a coordenada x do segundo ponto: ")
Dim x2 As Double = Double.Parse(Console.ReadLine())
Console.Write("Informe a coordenada y do segundo ponto: ")
Dim y2 As Double = Double.Parse(Console.ReadLine())
' agora vamos calcular o coeficiente angular
Dim m As Double = (y2 - y1) / (x2 - x1)
' e mostramos o resultado
Console.WriteLine("O coeficiente angular é: " & m)
Console.WriteLine("\nPressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código em linguagem VB.NET nós teremos o seguinte resultado: O coeficiente angular é: 0,6666666666666666 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
Imports System
Module Program
Sub Main(args As String())
' x e y do primeiro ponto
Console.Write("Informe a coordenada x do primeiro ponto: ")
Dim x1 As Double = Double.Parse(Console.ReadLine())
Console.Write("Informe a coordenada y do primeiro ponto: ")
Dim y1 As Double = Double.Parse(Console.ReadLine())
' x e y do segundo ponto
Console.Write("Informe a coordenada x do segundo ponto: ")
Dim x2 As Double = Double.Parse(Console.ReadLine())
Console.Write("Informe a coordenada y do segundo ponto: ")
Dim y2 As Double = Double.Parse(Console.ReadLine())
' vamos obter o comprimento do cateto oposto
Dim cateto_oposto As Double = y2 - y1
' e agora o cateto adjascente
Dim cateto_adjascente As Double = x2 - x1
' vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
' (em radianos, não se esqueça)
Dim tetha As Double = Math.Atan2(cateto_oposto, cateto_adjascente)
' e finalmente usamos a tangente desse ângulo para calcular
' o coeficiente angular
Dim tangente As Double = Math.Tan(tetha)
' e mostramos o resultado
Console.WriteLine("O coeficiente angular é: " & tangente)
Console.WriteLine("\nPressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Java ::: Dicas & Truques ::: Aplicativos e Outros |
Como calcular a distância entre dois pontos na terra em JavaQuantidade de visualizações: 1264 vezes |
|
Nesta dica mostrarei como calcular a distância em quilômetros entre dois pontos na terra dadas suas latitudes e longitudes. Neste exemplo eu coloquei o valor de 6378.137 para o raio da terra, mas você pode definir para o valor que achar mais adequado. O cálculo usado neste código se baseia na Fórmula de Haversine, que determina a distância do grande círculo entre dois pontos em uma esfera, dadas suas longitudes e latitudes. Veja o código Java completo:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
// vamos usar a classe Scanner para ler os
// valores de latitudes e longitudes
Scanner entrada = new Scanner(System.in);
System.out.print("Informe a primeira latitude: ");
double lat1 = Double.parseDouble(entrada.nextLine());
System.out.print("Informe a primeira longitude: ");
double lon1 = Double.parseDouble(entrada.nextLine());
System.out.print("Informe a segunda latitude: ");
double lat2 = Double.parseDouble(entrada.nextLine());
System.out.print("Informe a segunda longitude: ");
double lon2 = Double.parseDouble(entrada.nextLine());
// vamos calcular a distância entre os dois pontos em Kms
double distancia = calcularDistancia(lat1, lat2, lon1, lon2);
// mostramos o resultado
System.out.println("A distância entre os dois pontos é: " +
distancia + "kms");
System.out.println("\n");
}
// função que recebe dois pontos na terra e retorna a distância
// entre eles em quilômetros
public static double calcularDistancia(double lat1,
double lat2, double lon1, double lon2){
double raio_terra = 6378.137; // raio da terra em quilômetros
// o primeiro passo é converter as latitudes e longitudes
// para radianos
lon1 = Math.toRadians(lon1);
lon2 = Math.toRadians(lon2);
lat1 = Math.toRadians(lat1);
lat2 = Math.toRadians(lat2);
// agora aplicamos a Fórmula de Haversine
double dlon = lon2 - lon1;
double dlat = lat2 - lat1;
double a = Math.pow(Math.sin(dlat / 2), 2) + Math.cos(lat1) * Math.cos(lat2)
* Math.pow(Math.sin(dlon / 2),2);
double c = 2 * Math.asin(Math.sqrt(a));
// e retornamos a distância
return(c * raio_terra);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Informe a primeira latitude: -16.674551 Informe a primeira longitude: -49.303598 Informe a segunda latitude: -15.579321 Informe a segunda longitude: -56.10009 A distância entre os dois pontos é: 736.9183827638687kms Neste exemplo eu calculei a distância entre as cidades de Goiânia-GO e Cuiabá-MT. A latitude é a distância ao Equador medida ao longo do meridiano de Greenwich. Esta distância mede-se em graus, podendo variar entre 0o e 90o para Norte(N) ou para Sul(S). A longitude é a distância ao meridiano de Greenwich medida ao longo do Equador. |
Python ::: Matplotlib Python Library (Biblioteca Python Matplotlib) ::: Passos Iniciais |
Plotagem e visualização de dados em Python - Como instalar a biblioteca Matplotlib e testar seu funcionamentoQuantidade de visualizações: 3250 vezes |
|
A biblioteca Matplotlib, escrita originalmente por John D. Hunter em 2003, é um dos pacotes Python mais populares para a plotagem e visualização de dados. O acesso às funcionalidades da Matplotlib é feito por meio da interface Pylab, que lembra muito o MATLAB, a linguagem de programação proprietária desenvolvida pela MathWorks. Os usuários acostumados com essa ferramenta chegam a afirmar que a biblioteca Matplotlib, combinada com a biblioteca NumPy, pode ser considerada o equivalente open source do MATLAB. Já tenho o Matplotlib disponível na minha instalação do Python? Antes de iniciar qualquer projeto que envolva a biblioteca Matplotlib, é importante verificar se a mesma está disponível em sua instalação do Python. Isso pode ser de várias formas. Mostrarei como obter a lista de módulos usando a opção "list" do pip. Basta abrir uma janela de terminal e disparar o seguinte comando: C:\Users\Osmar>pip list Você terá um resultado parecido com: C:\Users\Osmar>pip list Package Version ----------------- ------- astroid 2.4.2 colorama 0.4.4 isort 5.6.4 joblib 1.0.0 lazy-object-proxy 1.4.3 mccabe 0.6.1 numpy 1.19.4 pandas 1.1.5 Pillow 8.0.1 pip 20.3.3 pylint 2.6.0 python-dateutil 2.8.1 pytz 2020.4 scikit-learn 0.24.0 scipy 1.5.4 setuptools 49.2.1 six 1.15.0 threadpoolctl 2.1.0 toml 0.10.2 wrapt 1.12.1 wxPython 4.1.1
# importamos a bibliteca Matplotlib
import matplotlib as mp
def main():
# vamos mostrar a versão da biblioteca Matplotlib
versao = mp.__version__
print("A versão do Matplotlib é:", versao)
if __name__== "__main__":
main()
Se você tiver o Matplotlib instalado, o resultado desse código será algo como: A versão do Matplotlib é: 3.4.1 Se você não tiver a biblioteca Matplotlib instalada, a seguinte mensagem de erro será exibida: Exception has occurred: ModuleNotFoundError File "c:\estudos_python\estudos.py", line 3, in <module> import matplotlib as mp ModuleNotFoundError: No module named 'matplotlib' Não tenho o Matplotlib ainda. O que faço? Abra uma janela de terminal e dispare o comando abaixo: C:\Users\Osmar>pip install matplotlib Depois de alguns segundos você verá o seguinte resultado: Collecting matplotlib Downloading matplotlib-3.4.1-cp39-cp39-win_amd64.whl (7.1 MB) |-| 7.1 MB 3.3 MB/s Requirement already satisfied: pillow>=6.2.0 in c:\python_3_9_1\lib\site-packages (from matplotlib) (8.0.1) Requirement already satisfied: python-dateutil>=2.7 in c:\python_3_9_1\lib\site-packages (from matplotlib) (2.8.1) Requirement already satisfied: numpy>=1.16 in c:\python_3_9_1\lib\site-packages (from matplotlib) (1.19.4) Collecting cycler>=0.10 Downloading cycler-0.10.0-py2.py3-none-any.whl (6.5 kB) Requirement already satisfied: six in c:\users\osmar\appdata\roaming\python\python39\site-packages (from cycler>=0.10->matplotlib) (1.15.0) Collecting kiwisolver>=1.0.1 Downloading kiwisolver-1.3.1-cp39-cp39-win_amd64.whl (51 kB) |-| 51 kB 3.8 MB/s Collecting pyparsing>=2.2.1 Downloading pyparsing-2.4.7-py2.py3-none-any.whl (67 kB) |-| 67 kB 1.7 MB/s Installing collected packages: pyparsing, kiwisolver, cycler, matplotlib Successfully installed cycler-0.10.0 kiwisolver-1.3.1 matplotlib-3.4.1 pyparsing-2.4.7 Obteve resultado parecido? Pronto! Você já pode começar a usar a biblioteca Matplotlib em seus aplicações Python. |
C ::: C para Engenharia ::: Física - Mecânica |
Como calcular a velocidade da queda livre de um corpo dado o intervalo de tempo (e a aceleração da gravidade) em CQuantidade de visualizações: 2596 vezes |
|
A Queda Livre é um Movimento Uniformemente Variado, na qual um objeto em queda livre tem a sua velocidade aumentada a taxas constantes. Abandonado em alturas próximas da terra, a velocidade com que um corpo cai aumenta a uma taxa de aproximadamente 9,8m/s. Isso é o mesmo que dizer que a aceleração da gravidade terrestre é de 9,8m/s2, o que aumenta a velocidade do objeto em 35,28km/h a cada segundo. Assim, a fórmula da velocidade de um objeto em queda livre é: \[ \text{v} = \text{g} \cdot \text{t} \] Onde: v ? velocidade de queda (m/s) g ? aceleração da gravidade (m/s2) t ? intervalo de tempo (s) Vamos ver um exemplo? Veja o seguinte enunciado: 1) Um corpo é abandonado a uma altura qualquer no tempo 0s e está em queda livre. Calcule a sua velocidade no tempo 15s. Como sabemos que o intervalo de tempo é 15s, só precisamos jogar na fórmula. Veja o código C completo para o cálculo:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
// gravidade terrestre em m/s2
float gravidade = 9.80665;
// intervalo de tempo da queda livre (em segundos)
float tempo = 15.00; // em segundos
// velocidade da queda nesse intervalo
float velocidade = gravidade * tempo;
// mostramos o resultado
printf("A velocidade da queda livre é: %fm/s",
velocidade);
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: A velocidade da queda livre é: 147.099747m/s Se quisermos saber a velocidade em km/h, basta multiplicar o resultado por 3.6, o que dará 529.56km/h. Vamos tornar o experimento mais interessante? Veja uma modificação no código C que mostra a velocidade da queda nos 10 primeiros segundos, de forma individual:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
int i; // variável de controle do laço
// gravidade terrestre em m/s2
float gravidade = 9.80665;
// intervalo de tempo da queda livre (em segundos)
int tempo;
// velocidade da queda nesse intervalo
float velocidade;
// um laço for que repete 10 vezes
for(i = 1; i <= 10; i++){
tempo = i; // inicialmente será um segundo
velocidade = gravidade * tempo;
printf("A velocidade no tempo %d: %fm/s\n",
tempo, velocidade);
}
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: A velocidade no tempo 1: 9.806650m/s A velocidade no tempo 2: 19.613300m/s A velocidade no tempo 3: 29.419950m/s A velocidade no tempo 4: 39.226601m/s A velocidade no tempo 5: 49.033249m/s A velocidade no tempo 6: 58.839901m/s A velocidade no tempo 7: 68.646553m/s A velocidade no tempo 8: 78.453201m/s A velocidade no tempo 9: 88.259850m/s A velocidade no tempo 10: 98.066498m/s |
Você também poderá gostar das dicas e truques de programação abaixo |
|
C - Como escrever uma função strtoupper() em C para transformar uma palavra inteira em letras maiúsculas VB.NET - Como calcular o coeficiente angular de uma reta em VB.NET dados dois pontos no plano cartesiano |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





