C++ ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em C++ dados dois pontos no plano cartesianoQuantidade de visualizações: 1401 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem C++ que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
#include <iostream>
#include <cstdlib>
using namespace std;
int main(int argc, char *argv[]){
// coordenadas dos dois pontos
float x1, y1, x2, y2;
// guarda o coeficiente angular
float m;
// x e y do primeiro ponto
cout << "Coordenada x do primeiro ponto: ";
cin >> x1;
cout << "Coordenada y do primeiro ponto: ";
cin >> y1;
// x e y do segundo ponto
cout << "Coordenada x do segundo ponto: ";
cin >> x2;
cout << "Coordenada y do segundo ponto: ";
cin >> y2;
// vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1);
// mostramos o resultado
cout << "O coeficiente angular é: " << m << "\n\n";
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
Ao executar este código C++ nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.666667 Pressione qualquer tecla para continuar... Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
#include <iostream>
#include <cstdlib>
#include <math.h>
using namespace std;
int main(int argc, char *argv[]){
// coordenadas dos dois pontos
float x1, y1, x2, y2;
// guarda os comprimentos dos catetos oposto e adjascente
float cateto_oposto, cateto_adjascente;
// guarda o ângulo tetha (em radianos) e a tangente
float tetha, tangente;
// x e y do primeiro ponto
cout << "Coordenada x do primeiro ponto: ";
cin >> x1;
cout << "Coordenada y do primeiro ponto: ";
cin >> y1;
// x e y do segundo ponto
cout << "Coordenada x do segundo ponto: ";
cin >> x2;
cout << "Coordenada y do segundo ponto: ";
cin >> y2;
// vamos obter o comprimento do cateto oposto
cateto_oposto = y2 - y1;
// e agora o cateto adjascente
cateto_adjascente = x2 - x1;
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
tetha = atan2(cateto_oposto, cateto_adjascente);
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
tangente = tan(tetha);
// mostramos o resultado
cout << "O coeficiente angular é: " << tangente << "\n\n";
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Dart ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como testar se um ponto está dentro de um círculo em Dart - Desenvolvimento de Games com DartQuantidade de visualizações: 874 vezes |
|
Quando estamos trabalhando com computação gráfica, geometria e trigonometria ou desenvolvimento de jogos em Dart, é comum precisarmos verificar se um determinado ponto (uma coordenada x, y) está contido dentro de um círculo. Para melhor entendimento, veja a imagem a seguir: 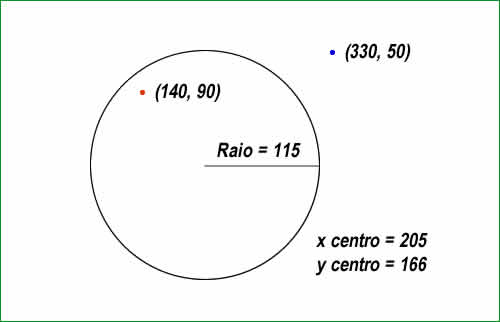 Veja que temos um círculo com raio igual a 115 e com centro nas coordenadas (x = 205; y = 166). Temos também dois pontos. O ponto vermelho está nas coordenadas (x = 140; y = 90) e o ponto azul está nas coordenadas (x = 330; y = 500. Como podemos ver na imagem, o ponto vermelho está dentro do círculo, enquanto o ponto azul está fora. E nosso intenção nesta dica é escrever o código Dart que permite fazer essa verificação. Tenha em mente que está técnica é muito útil para o teste de colisões no desenvolvimento de games. Veja o código completo para o exemplo:
// Vamos importar a biblioteca dart:io
import "dart:io";
// vamos importar a biblioteca dart:math
import "dart:math";
// vamos declarar a classe Circulo
class Circulo{
double xc;
double yc;
double raio;
// construtor da classe Circulo
Circulo(double xc, double yc, double raio){
this.xc = xc; // x do centro
this.yc = yc; // y do centro
this.raio = raio; // raio do círculo
}
}
// agora vamos declarar a classe Ponto
class Ponto{
double x;
double y;
// construtor da classe Ponto
Ponto(double x, double y){
this.x = x; // coordenada x
this.y = y; // coordenada y
}
}
void main(){
// variáveis que vamos usar na resolução do problema
Circulo c;
Ponto p;
double dx, dy;
// vamos criar um objeto Circulo
c = new Circulo(205, 166, 115);
// vamos criar um objeto Ponto
p = new Ponto(140, 90);
// vamos verificar se o ponto está dentro do
// círculo
dx = p.x - c.xc;
dy = p.y - c.yc;
if((pow(dx, 2) + pow(dy, 2)) < pow(c.raio, 2)){
stdout.write("O ponto está dentro do círculo");
}
else{
stdout.write("O ponto NÃO está dentro do círculo");
}
}
Ao executar este código Dart nós teremos o seguinte resultado: O ponto está dentro do círculo. Experimente com círculos de raios e coordenadas centrais diferentes e também com pontos em várias coordenadas e veja como os resultados são interessantes. |
C# ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Como usar o laço do...while da linguagem C#Quantidade de visualizações: 11878 vezes |
O laço do...while (faça...enquanto) é usado quando queremos repetir uma instrução ou bloco de instruções ENQUANTO uma condição for satisfatória. A única diferença entre este laço e o laço while, é que, no laço do...while a condição de parada é testada após a iteração, o que garante que o laço do...while será executado no mínimo uma vez. No laço while a condição é testada antes da iteração. Veja um exemplo:
static void Main(string[] args){
int valor = 1;
do{
Console.WriteLine("{0}", valor);
valor++;
}while(valor <= 10);
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
Este trecho de código conta de 1 até 10. Veja que após cada iteração do laço nós testamos se o valor da variável de controle é menor ou igual a 10. A próxima iteração acontece somente se esta condição for satisfeita. Note ainda que dentro de cada iteração nós incrementamos o valor da variável de controle. Isso é feito para que o laço não seja executado infinitamente. Veja um outro exemplo de laço do...while, desta vez simulando um menu de opções:
static void Main(string[] args){
// variável que registra a opção do usuário
int opcao;
// laço do..while que mostra as opções do menu enquanto
// o valor -1 não for informado
do{
// lê a opção
Console.Write("Informe a opção 1, 2 ou 3" +
" (-1 para sair): ");
opcao = int.Parse(Console.ReadLine());
switch (opcao){
case 1:
Console.WriteLine("Executando a opção 1");
break;
case 2:
Console.WriteLine("Executando a opção 2");
break;
case 3:
Console.WriteLine("Executando a opção 3");
break;
default:
Console.WriteLine("Opção incorreta");
break;
}
}while(opcao != -1);
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
O laço do...while não é tão usado quanto o laço while. Use-o naquelas situações em que o laço deverá ser executado no mínimo uma vez. |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Sistemas Digitais - Manipulação de Bits |
Exercícios Resolvidos de Java - Como fazer o complemento de 1 de um número binário em Java - Solução usando manipulação de stringsQuantidade de visualizações: 463 vezes |
|
Pergunta/Tarefa: Em Sistemas Digitais e na manipulação de bits, o complemento de 1 de um número binário é realizado de forma direta invertendo-se os "0s" e "1s", ou seja, todo zero (0) vira um (1) e todo um (1) vira zero (0). Dessa forma, se tivermos o número binário 11001, seu complemento de 1 será 00110. Escreva um programa Java que pede para o usuário informar um número binário e exiba o seu complemento de um. Para esta solução você deverá usar exclusivamente manipulação de strings. Sua saída deve ser parecida com: Informe um número binário: 1011001 O complemento de 1 é: 0100110 Veja a resolução comentada deste exercício usando Java:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// vamos solicitar um número binário
System.out.print("Informe um número binário: ");
String binario = entrada.nextLine();
// vamos converter a string em um arrays de chars
char digitos[] = binario.toCharArray();
// agora percorremos todos os dígitos do número binário
// e trocamos os "0s" por "1s" e vice-versa
for(int i = 0; i < digitos.length; i++){
if(digitos[i] == '0'){
digitos[i] = '1';
}
else{
digitos[i] = '0';
}
}
// convertemos de novo para string
String complemento1 = String.valueOf(digitos);
// e mostramos o resultado
System.out.println("O complemento de 1 é: " + complemento1);
}
}
|
C# ::: Dicas & Truques ::: Strings e Caracteres |
Como converter uma string em um array de char em C# usando a função ToCharArray()Quantidade de visualizações: 9990 vezes |
|
Nesta dica mostrarei como podemos usar a função ToCharArray() da classe String da linguagem C# para converter todos os caracteres de uma palavra, frase ou texto em um vetor de chars. Em seguida nós usaremos o método Reverse() da classe Array para inverter a ordem dos elementos do vetor. Finalmente nós passamos este vetor para o construtor da classe String para obter a string original novamente, só que desta vez, com a ordem de suas letras invertidas. Veja o código C# completo para o exemplo:
using System;
namespace Estudos {
class Program {
static void Main(string[] args) {
string frase = "Gosto de C#";
Console.WriteLine("Frase original: " + frase);
// obtém um array de caracteres a partir da string
char[] letras = frase.ToCharArray();
Array.Reverse(letras); // inverte o array
// transforma em string novamente
string resultado = new String(letras);
Console.WriteLine("Frase invertida: " + resultado);
Console.WriteLine();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Frase original: Gosto de C# Frase invertida: #C ed otsoG |
C# ::: Dicas & Truques ::: Data e Hora |
Datas e horas em C# - Como obter a data atual no formato curto usando C#Quantidade de visualizações: 334 vezes |
|
Nesta dica mostrarei como obter a data atual usando a propriedade Now da classe DateTime e exibí-la no formato curto, ou seja, DD/MM/AAAA. Veja o código C# completo para o exemplo:
using System;
namespace Estudos{
class Program{
static void Main(string[] args) {
// data atual no formato curto
DateTime hoje = DateTime.Now;
System.Console.WriteLine("A data hoje é: {0:d}", hoje);
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código nós teremos o seguinte resultado: A data hoje é: 23/03/2021 |
C# ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em C# dados dois pontos no plano cartesianoQuantidade de visualizações: 1566 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem C# que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
using System;
using System.Collections;
namespace Estudos {
class Program {
static void Main(string[] args) {
// x e y do primeiro ponto
Console.Write("Informe a coordenada x do primeiro ponto: ");
double x1 = double.Parse(Console.ReadLine());
Console.Write("Informe a coordenada y do primeiro ponto: ");
double y1 = double.Parse(Console.ReadLine());
// x e y do segundo ponto
Console.Write("Informe a coordenada x do segundo ponto: ");
double x2 = double.Parse(Console.ReadLine());
Console.Write("Informe a coordenada y do segundo ponto: ");
double y2 = double.Parse(Console.ReadLine());
// agora vamos calcular o coeficiente angular
double m = (y2 - y1) / (x2 - x1);
// e mostramos o resultado
Console.WriteLine("O coeficiente angular é: " + m);
Console.WriteLine("\nPressione qualquer tecla para sair...");
// pausa o programa
Console.ReadKey();
}
}
}
Ao executar este código em linguagem C# nós teremos o seguinte resultado: O coeficiente angular é: 0,6666666666666666 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
using System;
using System.Collections;
namespace Estudos {
class Program {
static void Main(string[] args) {
// x e y do primeiro ponto
Console.Write("Informe a coordenada x do primeiro ponto: ");
double x1 = double.Parse(Console.ReadLine());
Console.Write("Informe a coordenada y do primeiro ponto: ");
double y1 = double.Parse(Console.ReadLine());
// x e y do segundo ponto
Console.Write("Informe a coordenada x do segundo ponto: ");
double x2 = double.Parse(Console.ReadLine());
Console.Write("Informe a coordenada y do segundo ponto: ");
double y2 = double.Parse(Console.ReadLine());
// vamos obter o comprimento do cateto oposto
double cateto_oposto = y2 - y1;
// e agora o cateto adjascente
double cateto_adjascente = x2 - x1;
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
double tetha = Math.Atan2(cateto_oposto, cateto_adjascente);
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
double tangente = Math.Tan(tetha);
// e mostramos o resultado
Console.WriteLine("O coeficiente angular é: " + tangente);
Console.WriteLine("\nPressione qualquer tecla para sair...");
// pausa o programa
Console.ReadKey();
}
}
}
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
GNU Octave ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cateto oposto dadas as medidas da hipotenusa e do cateto adjascente em GNU OctaveQuantidade de visualizações: 1122 vezes |
|
Todos estamos acostumados com o Teorema de Pitágoras, que diz que "o quadrado da hipotenusa é igual à soma dos quadrados dos catetos". Baseado nessa informação, fica fácil retornar a medida do cateto oposto quando temos as medidas da hipotenusa e do cateto adjascente. Isso, claro, via programação em linguagem GNU Octave. Comece observando a imagem a seguir:  Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. A medida da hipotenusa é, sem arredondamentos, 36.056 metros. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras): \[c^2 = a^2 + b^2\] Tudo que temos que fazer é mudar a fórmula para: \[a^2 = c^2 - b^2\] Veja que agora o quadrado do cateto oposto é igual ao quadrado da hipotenusa menos o quadrado do cateto adjascente. Não se esqueça de que a hipotenusa é o maior lado do triângulo retângulo. Veja agora como esse cálculo é feito em linguagem GNU Octave (script GNU Octave):
c = 36.056 # medida da hipotenusa
b = 30 # medida do cateto adjascente
# agora vamos calcular o comprimento da cateto oposto
a = sqrt(power(c, 2) - power(b, 2))
# e mostramos o resultado
fprintf("A medida do cateto oposto é: %f\n", a);
Ao executar este código GNU Octave nós teremos o seguinte resultado: A medida do cateto oposto é: 20.000878 Como podemos ver, o resultado retornado com o código GNU Octave confere com os valores da imagem apresentada. |
C ::: Dicas & Truques ::: Arquivos e Diretórios |
Como ler o conteúdo de um arquivo um caractere de cada vez usando a função fgetc() da linguagem CQuantidade de visualizações: 573 vezes |
|
A função fgetc() da linguagme C pode ser usada quando queremos ler o conteúdo de um arquivo um caractere de cada vez. Esta função retorna o caractere atualmente representado pelo indicador de posição interna no arquivo. Depois de lido o caractere, o indicador de posição avança para apontar para o próximo caractere. Veja a assinatura desta função: int fgetc(FILE *file); O trecho de código abaixo mostra como usar um laço while para ler todos os caracteres do arquivo especificado e exibir o conteúdo na tela:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[])
{
FILE *arquivo = fopen("c:\\testes.txt", "r");
int caractere;
// testa se o arquivo foi aberto com sucesso
if(arquivo != NULL){
// vamos usar um laço para ler o conteúdo do arquivo
// e exibí-lo
while((caractere = fgetc(arquivo)) != EOF)
printf("%c", caractere);
fclose(arquivo); // libera o ponteiro para o arquivo
}
else
printf("Nao foi possivel abrir o arquivo.");
printf("\n\n");
system("PAUSE");
return 0;
}
|
C# ::: Windows Forms ::: TextBox |
Como definir a cor de fundo de uma caixa de texto TextBox do C# Windows Forms via códigoQuantidade de visualizações: 9143 vezes |
|
Nesta dica mostrarei como podemos usar a propriedade BackColor da classe Control do C# Windows Forms para definir a cor de fundo de uma caixa de texto TextBox. Note que criei uma TextBox com o nome textBox1 e estou chamando o código a partir do evento Click de um botão Button. Veja o trecho de código para o exemplo:
private void button1_Click(object sender, EventArgs e){
textBox1.BackColor = Color.YellowGreen;
}
|
Nossas 20 dicas & truques de programação mais populares |
|
JavaScript - JavaScript para iniciantes - Como converter uma string em um valor numérico usando o método Number() do JavaScript PHP - Datas e horas em PHP - Como subtrair horas de uma data usando a função mktime() da linguagem PHP |
Você também poderá gostar das dicas e truques de programação abaixo |
|
React.js - Aprenda a desenvolver aplicações React diretamente no HTML, sem usar a ferramenta create-react-app |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






