Java ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o comprimento da hipotenusa em Java dadas as medidas do cateto oposto e do cateto adjascenteQuantidade de visualizações: 1554 vezes |
Nesta dica mostrarei como é possível usar a linguagem Java para retornar o comprimento da hipotenusa dadas as medidas do cateto oposto e do cateto adjascente. Vamos começar analisando a imagem a seguir: Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras), tudo que temos a fazer a converter esta fórmula para código Java. Veja:
package arquivodecodigos;
public class Estudos{
public static void main(String args[]){
double a = 20; // medida do cateto oposto
double b = 30; // medida do cateto adjascente
// agora vamos calcular o comprimento da hipotenusa
double c = Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2));
// e mostramos o resultado
System.out.println("O comprimento da hipotenusa é: " +
c);
}
}
Ao executar este código Java nós teremos o seguinte resultado: O comprimento da hipotenusa é: 36.05551275463989 Como podemos ver, o resultado retornado com o código Java confere com os valores da imagem apresentada. |
Java ::: Java para Engenharia ::: Geometria Analítica e Álgebra Linear |
Java para Geometria Analítica e Álgebra Linear - Como efetuar a soma de matrizes usando JavaQuantidade de visualizações: 1797 vezes |
|
A soma de matrizes (assim como a subtração e multiplicação) é parte integrante da disciplina de Álgebra Linear e seu cálculo é muito simples. Assumindo duas matrizes A e B, ambas com a mesma quantidade de linhas e colunas, a matriz soma pode ser obtida da seguinte forma: \[A + B = \left[\begin{matrix} 3 & 4 & -1 \\ 8 & 2 & 1 \\ 7 & 5 & -3 \end{matrix}\right] + \left[\begin{matrix} -2 & 6 & 4 \\ 1 & 8 & 9 \\ -4 & 10 & 3 \end{matrix}\right] = \left[\begin{matrix} 1 & 10 & 3 \\ 9 & 10 & 10 \\ 3 & 15 & 0 \end{matrix}\right] \] Um elemento da matriz é representando por sua posição linha e coluna. Usamos a letra i para a linha e j para a coluna, ou seja, aij. Dessa forma, o elemento na primeira linha e primeira coluna da matriz é a11, o elemento na primeira linha e segunda coluna é a12 e assim por diante. Então, a soma das duas matrizes é feita da seguinte forma: Cij = Aij + Bij. E agora veja o código Java que declara duas matrizes matrizA e matrizB e obtém uma terceira (matrizC) contendo a soma das duas anteriores. Novamente, note o requisito de que as matrizes deverão ter o mesmo número de linhas e colunas:
package arquivodecodigos;
public class Estudos{
public static void main(String args[]){
// declarar, construir e inicializar as matrizes
int matrizA[][] = {{3, 4, -1}, {8, 2, 1}, {7, 5, -3}};
int matrizB[][] = {{-2, 6, 4}, {1, 8, 9}, {-4, 10, 3}};
// esta é a matriz soma
int matrizSoma[][] = new int[3][3];
// e agora vamos prosseguir com a soma
for(int i = 0; i < matrizA.length; i++){
for(int j = 0; j < matrizA[0].length; j++){
matrizSoma[i][j] = matrizA[i][j] + matrizB[i][j];
}
}
// vamos exibir os valores da primeira matriz
System.out.println("Elementos da matriz A:");
for(int i = 0; i < matrizA.length; i++){
for(int j = 0; j < matrizA[0].length; j++){
System.out.printf("%5d ", matrizA[i][j]);
}
System.out.println();
}
// vamos exibir os valores da primeira matriz
System.out.println("\nElementos da matriz B:");
for(int i = 0; i < matrizB.length; i++){
for(int j = 0; j < matrizB[0].length; j++){
System.out.printf("%5d ", matrizB[i][j]);
}
System.out.println();
}
// vamos exibir os valores da matriz soma
System.out.println("\nElementos da matriz soma:");
for(int i = 0; i < matrizSoma.length; i++){
for(int j = 0; j < matrizSoma[0].length; j++){
System.out.printf("%5d ", matrizSoma[i][j]);
}
System.out.println();
}
}
}
Ao executar este código Java nós teremos o seguinte resultado:
Elementos da matriz A:
3 4 -1
8 2 1
7 5 -3
Elementos da matriz B:
-2 6 4
1 8 9
-4 10 3
Elementos da matriz soma:
1 10 3
9 10 10
3 15 0
|
VB.NET ::: Dicas & Truques ::: Matemática e Estatística |
Como calcular juros simples e montante em VB.NETQuantidade de visualizações: 8655 vezes |
|
O regime de juros será simples quando o percentual de juros incidir apenas sobre o valor principal. Sobre os juros gerados a cada período não incidirão novos juros. Valor Principal ou simplesmente principal é o valor inicial emprestado ou aplicado, antes de somarmos os juros. Transformando em fórmula temos: J = P . i . n Onde: J = juros P = principal (capital) i = taxa de juros n = número de períodos Imaginemos uma dívida de R$ 2.000,00 que deverá ser paga com juros de 5% a.m. pelo regime de juros simples e o prazo para o pagamento é de 2 meses. O cálculo em VB.NET pode ser feito assim:
Module Module1
Sub Main()
Dim principal As Double = 2000.0
Dim taxa As Double = 0.08 '8%
Dim meses As Integer = 2
Dim juros As Double = principal * taxa * meses
Console.WriteLine("O total de juros a ser pago é: " _
& juros)
Console.WriteLine()
Console.WriteLine("Pressione uma tecla para sair...")
Console.ReadKey()
End Sub
End Module
O montante da dívida pode ser obtido das seguintes formas: a) Montante = Principal + Juros b) Montante = Principal + (Principal x Taxa de juros x Número de períodos) M = P . (1 + (i . n)) Veja o código:
Module Module1
Sub Main()
Dim principal As Double = 2000.0
Dim taxa As Double = 0.08 '8%
Dim meses As Integer = 2
Dim juros As Double = principal * taxa * meses
Dim montante As Double = principal * (1 + (taxa * meses))
Console.WriteLine("O total de juros a ser pago é: " _
& juros)
Console.WriteLine("O montante a ser pago é: " & montante)
Console.WriteLine()
Console.WriteLine("Pressione uma tecla para sair...")
Console.ReadKey()
End Sub
End Module
|
Ruby ::: Dicas & Truques ::: Strings e Caracteres |
Como concatenar strings em Ruby usando o operador <<Quantidade de visualizações: 8430 vezes |
Esta dica mostra como podemos usar o operador << para concatenar strings em Ruby. Veja: frase1 = "Gosto muito de Ruby" frase2 = " e de Python" # vamos concatenar as duas strings res = frase1 << frase2 # exibe o resultado puts res Ao executar este código Ruby nós teremos o seguinte resultado: Gosto muito de Ruby e de Python |
Java ::: Classes e Componentes ::: JMenuBar, JMenu, JMenuItem e Afins |
Java Swing - Como usar objetos da classe JCheckBoxMenuItem como itens de menu de suas aplicações Java SwingQuantidade de visualizações: 8915 vezes |
|
Neste exemplo mostrarei como usar objetos da classe JCheckBoxMenuItem como itens de um menu. Tais itens podem ser usados quando o usuário puder marcar uma ou mais opções, em um grupo relacionado de opções. Veja o resultado na imagem abaixo: 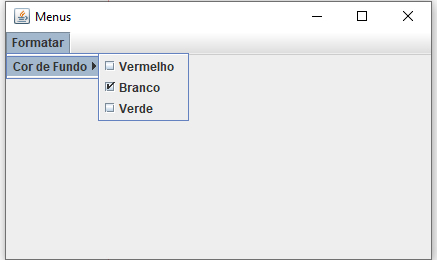 E agora o código completo para o exemplo:
package arquivodecodigos;
import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
public class Estudos extends JFrame{
JCheckBoxMenuItem cores[];
Color valCores[] = {Color.red, Color.white,
Color.green};
String nomeCores[] = {"Vermelho", "Branco",
"Verde"};
public Estudos(){
super("Menus");
// Cria a barra de menus
JMenuBar barra = new JMenuBar();
setJMenuBar(barra);
// Cria um menu
JMenu formatar = new JMenu("Formatar");
// Cria o menu de cor de fundo
JMenu item1 = new JMenu("Cor de Fundo");
// Adiciona o segundo JMenu ao primeiro
formatar.add(item1);
cores = new JCheckBoxMenuItem[valCores.length];
Gerenciador gerenciador = new Gerenciador();
for(int i = 0; i < valCores.length; i++){
cores[i] = new JCheckBoxMenuItem(nomeCores[i]);
item1.add(cores[i]);
cores[i].addItemListener(gerenciador);
}
// Adiciona o menu à barra de menus
barra.add(formatar);
setSize(300, 150);
setVisible(true);
}
public static void main(String args[]){
Estudos app = new Estudos();
app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
private class Gerenciador implements ItemListener{
public void itemStateChanged(ItemEvent e){
String marcadas = "As checkbox marcadas são:\n\n";
for(int i = 0; i < cores.length; i++){
if(cores[i].isSelected()){
marcadas += nomeCores[i] + "\n";
}
}
JOptionPane.showMessageDialog(null, marcadas);
}
}
}
|
JavaScript ::: Dicas & Truques ::: Strings e Caracteres |
Como converter uma string para letras minúsculas em JavaScript usando a função toLowerCase() do objeto StringQuantidade de visualizações: 2 vezes |
|
Nesta dica mostrarei como usar a função toLowerCase() do JavaScript para transformar todos os caracteres de uma palavra, frase ou texto para letras minúsculas. Esta função faz parte do objeto String. Veja um página HTML completa demonstrando o exemplo:
<!doctype html>
<html>
<head>
<title>Strings em JavaScript</title>
</head>
<body>
<script type="text/javascript">
var frase = "Veja Esta Frase.";
document.write("String original: " +
frase + "<br>");
// agora vamos transformar todos os caracteres
// da string para letras minúsculas
frase = frase.toLowerCase();
document.write("Em letras minúsculas: " +
frase + "<br>");
</script>
</body>
</html>
Ao executar este código JavaScript nós teremos o seguinte resultado: String original: Veja Esta Frase. Em letras minúsculas: veja esta frase. |
Python ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o arco cosseno de um número em Python usando o método acos() do módulo mathQuantidade de visualizações: 3539 vezes |
|
O arco cosseno, (também chamado de cosseno inverso) pode ser representado por cos-1 x, arccos x ou acos x. Esta função é a inversa do cosseno, ou seja, se o cosseno é a relação entre o cateto adjacente ao ângulo e a hipotenusa, o arco cosseno parte desta relação para encontrar o valor do ângulo. Em Python, o arco cosseno de um número pode ser obtido por meio do método acos() da classe Math. Este método recebe um valor double e retorna também um double, na faixa 0 <= x <= PI, onde PI vale 3.1416. Veja um código Python completo no qual informamos um número e em seguida calculamos o seu arco-cosseno:
# vamos importar o módulo Math
import math as math
def main():
numero = 0.5
print("O arco cosseno de %f é %f" % (numero, math.acos(numero)))
if __name__== "__main__":
main()
Ao executar este código nós teremos o seguinte resultado: O arco cosseno de 0.500000 é 1.047198 Não se esqueça de que as funções trigonométricas são usadas para modelar o movimento das ondas e fenômenos periódicos, como padrões sazonais. Elas formam a base para análises avançadas em engenharia elétrica, processamento digital de imagem, radiografia, termodinâmica, telecomunicações e muitos outros campos da ciência e da tecnologia. |
C++ ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como retornar o tamanho de um array em C++ - Curso de C++ - Vetores e matrizes em C++Quantidade de visualizações: 11129 vezes |
Muitas vezes precisamos saber a quantidade de elementos em vetor (array). Em C++, isso pode ser feito com o uso da função sizeof(). O que fazemos é obter a quantidade de bytes contidos em todo o vetor e depois dividimos pela quantidade de bytes no primeiro elemento. Veja o código:
#include <iostream>
using namespace std;
int main(int argc, char *argv[])
{
// declara e inicializa um array de 5 inteiros
int valores[5] = {43, 12, 8, 4, 102};
// obtém a quantidade de elementos na matriz
int quant = sizeof(valores) / sizeof(valores[0]);
// exibe o resultado
cout << "Quant. elementos : " << quant << endl;
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
Ao executarmos este código nós teremos o seguinte resultado: Quant. elementos : 5 |
C# ::: C# para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como somar os elementos da diagonal principal de uma matriz em C#Quantidade de visualizações: 2699 vezes |
|
A Matriz quadrada é um tipo especial de matriz que possui o mesmo número de linhas e o mesmo número de colunas, ou seja, dada uma matriz Anxm, ela será uma matriz quadrada se, e somente se, n = m, onde n é o número de linhas e m é o número de colunas. Em geral as matrizes quadradas são chamadas de Matrizes de Ordem n, onde n é o número de linhas e colunas. Dessa forma, uma matriz de ordem 4 é uma matriz que possui 4 linhas e quatro colunas. Toda matriz quadrada possui duas diagonais, e elas são muito exploradas tanto na matemática quanto na construção de algorítmos. Essas duas diagonais são chamadas de Diagonal Principal e Diagonal Secundária. A diagonal principal de uma matriz quadrada une o seu canto superior esquerdo ao canto inferior direito. Veja: 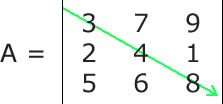 Nesta dica veremos como calcular a soma dos valores dos elementos da diagonal principal de uma matriz usando C#. Para isso, só precisamos manter em mente que a diagonal principal de uma matriz A é a coleção das entradas Aij em que i é igual a j. Assim, tudo que temos a fazer é converter essa regra para código C#. Veja um trecho de código C# completo no qual pedimos para o usuário informar os elementos da matriz e em seguida mostramos a soma dos elementos da diagonal superior:
using System;
namespace Estudos {
class Program {
static void Main(string[] args) {
// vamos declarar e construir uma matriz de três linhas
// e três colunas
int[,] matriz = new int[3, 3];
int soma_diagonal = 0; // guarda a soma dos elementos na diagonal
// principal
// vamos ler os valores para os elementos da matriz
for (int i = 0; i < matriz.GetLength(0); i++) { // linhas
for (int j = 0; j < matriz.GetLength(1); j++) { // colunas
Console.Write("Informe o valor para a linha " + i + " e coluna "
+ j + ": ");
matriz[i, j] = Int32.Parse(Console.ReadLine());
}
}
// vamos mostrar a matriz da forma que ela
// foi informada
Console.WriteLine();
// percorre as linhas
for (int i = 0; i < matriz.GetLength(0); i++) {
// percorre as colunas
for (int j = 0; j < matriz.GetLength(1); j++) {
Console.Write(" " + matriz[i, j]);
}
// passa para a próxima linha da matriz
Console.WriteLine();
}
// vamos calcular a soma dos elementos da diagonal
// principal
for (int i = 0; i < matriz.GetLength(0); i++) {
for (int j = 0; j < matriz.GetLength(1); j++) {
if (i == j) {
soma_diagonal = soma_diagonal + matriz[i, j];
}
}
}
// finalmente mostramos a soma da diagonal principal
Console.WriteLine("\nA soma dos elementos da diagonal principal é: "
+ soma_diagonal);
Console.WriteLine("\n\nPressione qualquer tecla para sair...");
// pausa o programa
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Informe o valor para a linha 0 e coluna 0: 3 Informe o valor para a linha 0 e coluna 1: 7 Informe o valor para a linha 0 e coluna 2: 9 Informe o valor para a linha 1 e coluna 0: 2 Informe o valor para a linha 1 e coluna 1: 4 Informe o valor para a linha 1 e coluna 2: 1 Informe o valor para a linha 2 e coluna 0: 5 Informe o valor para a linha 2 e coluna 1: 6 Informe o valor para a linha 2 e coluna 2: 8 3 7 9 2 4 1 5 6 8 A soma dos elementos da diagonal principal é: 15 |
Java ::: Pacote java.lang ::: Integer |
Java Básico - Como usar a constante SIZE da classe Integer para obter a quantidade de bits necessária para armazenar um intQuantidade de visualizações: 6817 vezes |
Em algumas situações gostaríamos de obter a quantidade de bits necessária para armazenar um valor do tipo int (inteiro). Para isso podemos usar a constante SIZE da classe Integer (uma classe wrapper que encapsula o valor primitivo int). Veja como isso pode ser feito:
public class Estudos {
public static void main(String[] args) {
// vamos obter a quantidade de bits necessária para representar um int
int quantBits = Integer.SIZE;
// o resultado
System.out.println("Um int ocupa " + quantBits + " bits, ou seja, " +
(quantBits / 8) + " bytes");
}
}
Ao executarmos este código o resultado será: Um int ocupa 32 bits, ou seja, 4 bytes. |
Nossas 20 dicas & truques de programação mais populares |
|
Java - Java Swing Avançado - Como exibir imagens nas células de uma JTable em suas aplicações Java Swing Python - Como testar se um ponto está dentro de um círculo em Python - Desenvolvimento de Games com Python |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Python - Como exibir os valores de 0 a 10 em ordem decrescente usando o laço for da linguagem Python Delphi - Como obter a quantidade de registros em um TClientDataSet do Delphi usando a propriedade RecordCount |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





