Java ::: Desafios e Lista de Exercícios Resolvidos ::: Java Básico |
Exercícios Resolvidos de Java - Lendo a idade de um nadador e classificando sua categoria como infantil, juvenil, adolescente, adulto ou sêniorQuantidade de visualizações: 3742 vezes |
|
Pergunta/Tarefa: Escreva um programa Java que solicita a idade de um nadador e classifica sua categoria de acordo com as seguintes regras: a) De 5 a 7 anos - Infantil; b) De 8 a 10 anos - Juvenil; c) De 11 a 15 anos - Adolescente; d) De 16 a 30 anos - Adulto; e) Acima de 30 anos - Sênior. Sua saída deverá ser parecida com: Informe sua idade: 19 Sua categoria é Adulto Veja a resolução comentada deste exercício usando Java console:
package estudos;
import java.util.Scanner;
public class Exercicio {
public static void main(String[] args) {
Scanner entrada = new Scanner(System.in);
// vamos solicitar a idade do nadador
System.out.print("Informe sua idade: ");
int idade = Integer.parseInt(entrada.nextLine());
// vamos verificar a categoria do nadador
if((idade >= 5) && (idade <= 7)){
System.out.println("Sua categoria é Infantil");
}
else if((idade >= 8) && (idade <= 10)){
System.out.println("Sua categoria é Juvenil");
}
else if((idade >= 11) && (idade <= 15)){
System.out.println("Sua categoria é Adolescente");
}
else if((idade >= 16) && (idade <= 30)){
System.out.println("Sua categoria é Adulto");
}
else if(idade > 30){
System.out.println("Sua categoria é Sênior");
}
else{
System.out.println("Não pertence a nenhuma categoria.");
}
System.out.println("\n");
}
}
|
Java ::: Classes e Componentes ::: JButton |
Como definir a cor do texto de um botão JButton do Java SwingQuantidade de visualizações: 9492 vezes |
|
Nesta dica eu mostrarei como é possível definir a cor do texto de um componente JButton do Java Swing. Para isso nós usamos o método setForeground() da classe JButton, fornecendo a cor desejada, por exemplo, Color.RED. Veja um exemplo Java Swing completo:
package arquivodecodigos;
import java.awt.*;
import javax.swing.*;
public class Estudos extends JFrame{
public Estudos() {
super("Estudos Swing");
Container c = getContentPane();
c.setLayout(new FlowLayout(FlowLayout.LEFT));
// Cria um JButton com a cor do texto vermelho
JButton btn1 = new JButton("Clique Aqui!");
btn1.setForeground(Color.RED);
// Cria um JButton com a cor de fundo verde
JButton btn2 = new JButton("Clique Aqui!");
btn2.setForeground(Color.GREEN);
// Adiciona os botões à janela
c.add(btn1);
c.add(btn2);
setSize(350, 250);
setVisible(true);
}
public static void main(String args[]){
Estudos app = new Estudos();
app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
}
|
Python ::: Fundamentos da Linguagem ::: Métodos, Procedimentos e Funções |
Como usar os argumentos padrões das funções e métodos em PythonQuantidade de visualizações: 7664 vezes |
Geralmente quando efetuamos chamadas às funções, nosso código fica responsável por fornecer os valores para os argumentos da função. Em Python é possível termos argumentos padrões, e tais argumentos já podem ter um valor pré-definido. Desta forma, a passagem dos parâmetros se torna opcional. Veja um exemplo:
# função com argumento padrão
def erro(msg = "Houve um erro."):
print(msg)
def main():
# chamada à função fornecendo o argumento
erro("Erro desconhecido.")
# chamada à função sem fornecer o argumento
erro()
if __name__== "__main__":
main()
Ao executarmos este exemplo nós teremos o seguinte resultado: Erro desconhecido. Houve um erro. Veja mais um exemplo: # função com argumentos padrões def volume(comprimento = 1, largura = 1, altura = 1): return (comprimento * largura * altura) def main(): # chamada à função fornecendo um argumento print(volume(3)) # chamada à função fornecendo dois argumentos print(volume(4, 5)) # chamada à função fornecendo três argumentos print(volume(4, 5, 7)) # chamada à função fornecendo nenhum argumento print(volume()) if __name__== "__main__": main() Ao executarmos este exemplo nós teremos o seguinte resultado: 3 20 140 1 É importante observar que os argumentos padrões devem estar sempre à direita dos demais argumentos. Falhar em cumprir esta exigência pode causar um erro do tipo: SyntaxError: non-default argument follows default argument |
Java ::: Pacote java.lang ::: Integer |
Java Básico - Como usar a constante SIZE da classe Integer para obter a quantidade de bits necessária para armazenar um intQuantidade de visualizações: 6817 vezes |
Em algumas situações gostaríamos de obter a quantidade de bits necessária para armazenar um valor do tipo int (inteiro). Para isso podemos usar a constante SIZE da classe Integer (uma classe wrapper que encapsula o valor primitivo int). Veja como isso pode ser feito:
public class Estudos {
public static void main(String[] args) {
// vamos obter a quantidade de bits necessária para representar um int
int quantBits = Integer.SIZE;
// o resultado
System.out.println("Um int ocupa " + quantBits + " bits, ou seja, " +
(quantBits / 8) + " bytes");
}
}
Ao executarmos este código o resultado será: Um int ocupa 32 bits, ou seja, 4 bytes. |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Geometria Analítica e Álgebra Linear |
Exercício Resolvido de Java - Como calcular o quadrante de uma coordenada cartesiana em JavaQuantidade de visualizações: 806 vezes |
|
Pergunta/Tarefa: O Plano Cartesiano, ou Sistema de Coordenadas Cartesianas, é formado por duas retas reais perpendiculares, ou seja, o ângulo entre elas é de 90 graus. Essas retas determinam um único plano, que é denominado como sistema ortogonal de coordenadas cartesianas ou somente plano cartesiano. No ano de 1637, René Descartes teve a brilhante ideia de relacionar álgebra e geometria, dando início à conhecida geometria analítica, método que possibilita descrever a geometria utilizando uma menor quantidade de diagramas e desenhos. Apesar de os créditos dessa descoberta serem dados a Descartes, Pierre de Fermat já conhecia e utilizava alguns conceitos de geometria analítica, logo o plano cartesiano. Há quatro quadrantes no Sistema de Coordenadas Cartesianas, conforme a figura a seguir:  Como podemos ver, no primeiro quadrante, tanto o x quanto o y são positivos. No segundo quadrante o x é negativo e o y é positivo. No terceiro quadrante, tanto o x quanto o y são negativos. Por fim, no quarto quadrante, o x é positivo e o y é negativo. Escreva um programa Java que pede para o usuário informar os valores x e y de uma coordenada cartesiana e informe em qual quadrante essa coordenada se situa. Se os valores de x e y forem zero, informe que o ponto se situa na origem do plano cartesiano. Sua saída deverá ser parecida com: Informe o valor x da coordenada: 12 Informe o valor y da coordenada: -7 A coordenada (12,-7) está no Quarto Quadrante (+,-) Veja a resolução comentada deste exercício em Java:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// variáveis usadas na resolução do problema
int x, y;
// vamos pedir para o usuário informar as coordenadas
System.out.print("Informe o valor x da coordenada: ");
x = Integer.parseInt(entrada.nextLine());
System.out.print("Informe o valor y da coordenada: ");
y = Integer.parseInt(entrada.nextLine());
// a coordenada está no primeiro quadrante?
if (x > 0 && y > 0){
System.out.println("A coordenada (" + x + "," +
y + ") está no Primeiro Quadrante (+,+)");
}
// a coordenada está no segundo quadrante?
else if (x < 0 && y > 0){
System.out.println("A coordenada (" + x + "," +
y + ") está no Segundo Quadrante (-,+)");
}
// a coordenada está no terceiro quadrante?
else if (x < 0 && y < 0){
System.out.println("A coordenada (" + x + "," +
y + ") está no Terceiro Quadrante (-,-)");
}
// a coordenada está no quarto quadrante?
else if (x > 0 && y < 0){
System.out.println("A coordenada (" + x + "," +
y + ") está no Quarto Quadrante (+,-)");
}
// a coordenada está na origem
else{
System.out.println("A coordenada (" + x + "," +
y + ") está na origem");
}
}
}
|
C ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular a área de um círculo em C dado o raio do círculoQuantidade de visualizações: 8910 vezes |
A área de um círculo pode ser calculada por meio do produto entre a constante PI e a medida do raio ao quadrado (r2). Comece analisando a figura abaixo: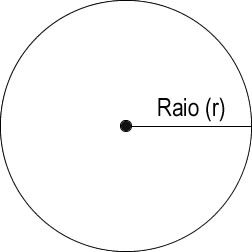 Sendo assim, temos a seguinte fórmula:  Onde A é a área, PI equivale a 3,14 (aproximadamente) e r é o raio do círculo. O raio é a medida que vai do centro até um ponto da extremidade do círculo. O diâmetro é a medida equivalente ao dobro da medida do raio, passando pelo centro do círculo e dividindo-o em duas partes. A medida do diâmetro é 2 * Raio. Veja agora um código C completo que calcula a área de um círculo mediante a informação do raio:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
// vamos definir o valor de PI
#define PI 3.14159265358979323846
int main(int argc, char *argv[]){
int raio;
printf("Informe o raio do círculo: ");
// efetua a leitura do raio
scanf("%d", &raio);
// calcula a área
double area = PI * pow(raio, 2);
// mostra o resultado
printf("A area do círculo de raio %d é igual a %f\n\n",
raio, area);
system("PAUSE");
return 0;
}
Ao executarmos este código nós teremos o seguinte resultado: Informe o raio do círculo: 5 A area do círculo de raio 5 é igual a 78.539816 A circunferência é um conjunto de pontos que estão a uma mesma distância do centro. Essa distância é conhecida como raio. A circunferência é estudada pela Geometria Analítica e, em geral, em um plano cartesiano. O círculo, que é formado pela circunferência e pelos infinitos pontos que preenchem seu interior, é estudado pela Geometria Plana, pois ele ocupa um espaço e pode ter sua área calculada, diferentemente da circunferência. |
Ruby ::: Dicas & Truques ::: Strings e Caracteres |
Como inverter uma string em Ruby usando as funções reverse e reverse!Quantidade de visualizações: 10027 vezes |
Esta dica mostra como podemos inverter uma string em Ruby, ou seja, reverter a ordem de seus caracteres. Para isso nós temos dois métodos: reverse e reverse!. O método reverse retorna uma nova string enquanto reverse! reverte o conteúdo da string original. Veja o trecho de código:# declara e inicializa uma variável string frase = "Osmar J. Silva" # inverte a string sem afetar o original invertida = frase.reverse # exibe o resultado puts "Original: " + frase puts "Invertida: " + invertida # inverte afetando o original frase.reverse! # exibe o resultado puts "Original: " + frase Ao executar este código Ruby nós teremos o seguinte resultado: Original: Osmar J. Silva Invertida: avliS .J ramsO Original: avliS .J ramsO |
JavaScript ::: JavaScript para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular a distância entre dois pontos no plano em JavaScript - JavaScript para Geometria Analítica e Álgebra LinearQuantidade de visualizações: 4968 vezes |
|
Como calcular a Distância Euclidiana entre dois pontos usando JavaScript Em várias aplicações envolvendo geometria, principalmente no desenvolvimento de jogos em JavaScript, é comum nos depararmos com a necessidade de calcular a distância entre dois pontos A e B. Nessa dica mostrarei como efetuar esse cálculo no R2, ou seja, no plano. Em outra dica eu abordo o cálculo no R3 (espaço). Comece analisando a imagem abaixo:  Veja que temos um ponto A (x = 3; y = 6) e um ponto B (x = 9; y = 4). Para determinarmos a distância entre esses dois pontos no plano cartesiano, temos que realizar a análise tanto no sentido do eixo das abscissas (x) quanto no do eixo das ordenadas (y). Veja a fórmula: \[d_{AB} = \sqrt{\left(x_b - x_a\right)^2 + \left(y_b - y_a\right)^2}\] Agora, jogando os valores dos dois pontos da fórmula nós teremos: \[d_{AB} = \sqrt{\left(9 - 3\right)^2 + \left(6 - 4\right)^2}\] Que resulta em 6,32 (aproximadamente). E agora veja o código JavaScript completo que define as coordenadas dos dois pontos e mostra a distância entre eles:
<html>
<head>
<title>Estudos JavaScript</title>
</head>
<body>
<script type="text/javascript">
// função que permite calcular a distância
// entre dois pontos no plano (R2)
function distancia2d(x1, y1, x2, y2){
var a = x2 - x1;
var b = y2 - y1;
var c = Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2));
return c;
}
// vamos definir os dados do primeiro ponto
var x1 = 3;
var y1 = 6;
// vamos ler os dados do segundo ponto
var x2 = 9;
var y2 = 4;
// vamos obter a distância entre eles
var distancia = distancia2d(x1, y1, x2, y2);
document.writeln("Distância entre os dois pontos: " +
distancia);
</script>
</body>
</html>
Ao executarmos este código JavaScript nós teremos o seguinte resultado: Distância entre os dois pontos: 6.324555320336759 |
Ruby ::: Dicas & Truques ::: Data e Hora |
Como usar a classe DateTime da linguagem RubyQuantidade de visualizações: 7314 vezes |
|
A classe DateTime da linguagem Ruby extende a classe Date e inclui horas, minutos, segundos e frações de segundo. Além disso, esta classe fornece suporte básico a fuso horários. Fuso horários são representados como uma diferença do UTC (Universal Coordinated Time) em fração de um dia. Esta diferença é quanto a hora local é mais cedo ou mais tarde que o UTC. Uma diferença de UTC 0 está centralizada na Inglaterra (também conhecido como GMT). À medida que viajamos para o leste, a diferença aumenta até que alcancemos a linha de separação de data no meio do Oceano Pacífico. Quando viajamos para o oeste, a diferença diminui. Esta diferença é abreviada como "of" na classe Date. Veja um trecho de código no qual usamos a classe DateTime para obter a data e hora atual:
# importa o módulo date
require "date"
# obtém a data e hora atual
agora = DateTime::now
# exibe o resultado
puts "Agora é " + agora.strftime("%e/%m/%Y - %H:%M:%S")
Ao executar este código Ruby nós teremos o seguinte resultado: Agora é 5/04/2022 - 11:51:06 |
Delphi ::: Dicas & Truques ::: Aplicativos e Outros |
Como calcular a distância entre dois pontos na terra em DelphiQuantidade de visualizações: 1461 vezes |
|
Nesta dica mostrarei como calcular a distância em quilômetros entre dois pontos na terra dadas suas latitudes e longitudes. Neste exemplo eu coloquei o valor de 6378.137 para o raio da terra, mas você pode definir para o valor que achar mais adequado. O cálculo usado neste código se baseia na Fórmula de Haversine, que determina a distância do grande círculo entre dois pontos em uma esfera, dadas suas longitudes e latitudes. Veja o código Delphi completo:
// função que recebe dois pontos na terra e retorna a distância
// entre eles em quilômetros
function CalcularDistancia(lat1: double; lat2: double; lon1: double;
lon2: double): double;
var
raio_terra, dlon, dlat, a, c: double;
begin
raio_terra := 6378.137; // raio da terra em quilômetros
// o primeiro passo é converter as latitudes e longitudes
// para radianos
// não esqueça de adicionar a unit Math
lon1 := DegToRad(lon1);
lon2 := DegToRad(lon2);
lat1 := DegToRad(lat1);
lat2 := DegToRad(lat2);
// agora aplicamos a Fórmula de Haversine
dlon := lon2 - lon1;
dlat := lat2 - lat1;
a := Power(Sin(dlat / 2), 2) + Cos(lat1) * Cos(lat2)
* Power(Sin(dlon / 2),2);
c := 2 * ArcSin(Sqrt(a));
// e retornamos a distância
Result := (c * raio_terra);
end;
procedure TForm5.Button1Click(Sender: TObject);
var
lat1, lon1, lat2, lon2, distancia: double;
begin
// obtém as coordenadas vindas dos campos de texto
lat1 := StrToFloat(txtPrimeiraLatitude.Text);
lon1 := StrToFloat(txtPrimeiraLongitude.Text);
lat2 := StrToFloat(txtSegundaLatitude.Text);
lon2 := StrToFloat(txtSegundaLongitude.Text);
// vamos calcular a distância entre os dois pontos em Kms
distancia := CalcularDistancia(lat1, lat2, lon1, lon2);
// e mostramos o resultado
txtDistancia.Text := FormatFloat('#.0', distancia) + ' kms';
end;
Ao executar este código Delphi nós teremos o seguinte resultado: Informe a primeira latitude: -16,674551 Informe a primeira longitude: -49,303598 Informe a segunda latitude: -15,579321 Informe a segunda longitude: -56,10009 A distância entre os dois pontos é: 736,9 kms Aqui as informações sobre as latitudes e longitudes vieram de campos de texto TEdit, e o código foi disparado a partir do clique de um botão TButton. Neste exemplo eu calculei a distância entre as cidades de Goiânia-GO e Cuiabá-MT. A latitude é a distância ao Equador medida ao longo do meridiano de Greenwich. Esta distância mede-se em graus, podendo variar entre 0o e 90o para Norte(N) ou para Sul(S). A longitude é a distância ao meridiano de Greenwich medida ao longo do Equador. |
Nossas 20 dicas & truques de programação mais populares |
|
Java - Como inserir uma substring em uma string em Java usando o método insert() da classe StringBuffer |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Android Java - Como usar a classe Toast em suas aplicações Android |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





