 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Data e Hora |
Exercícios Resolvidos de Java - Datas e horas - Escreva um programa Java que mostre a hora atual no formato HH:MM:SSQuantidade de visualizações: 3210 vezes |
|
Exercício Resolvido de Java - Datas e horas - Escreva um programa Java que mostre a hora atual no formato HH:MM:SS Pergunta/Tarefa: Escreva um programa Java console que mostre a hora atual no formato HH:MM:SS, ou seja, algo parecido com 23:43:15. Dica: Você pode usar várias classes Java para obter a hora atual. Não precisa se prender à classe que usei na resolução do exercício. Sua saída deverá ser parecida com: 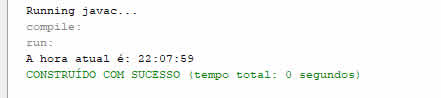 Resposta/Solução:
package arquivodecodigos;
import java.time.LocalDateTime;
import java.time.format.DateTimeFormatter;
public class Estudos{
public static void main(String[] args){
DateTimeFormatter dtf = DateTimeFormatter.ofPattern("HH:mm:ss");
LocalDateTime agora = LocalDateTime.now();
System.out.println("A hora atual é: " + dtf.format(agora));
}
}
|
C ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como declarar e inicializar um array unidimensional em C usando a notação {}Quantidade de visualizações: 14646 vezes |
A notação {} é muito conveniente quando precisamos declarar e inicializar um vetor ou uma matriz em apenas uma linha. Veja o trecho de código abaixo:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[])
{
// declara e inicializa um array de 5 inteiros
int valores[5] = {43, 12, 8, 4, 102};
int i;
// exibe os valores do array
for(i = 0; i < 5; i++){
printf("%d\n", valores[i]);
}
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: 43 12 8 4 102 |
LISP ::: Fundamentos da Linguagem ::: Estruturas de Controle |
Como usar o laço loop para contar de 1 até 10 em LispQuantidade de visualizações: 760 vezes |
|
A estrutura de repetição loop da linguagem Common Lisp é o laço mais simples fornecido pela linguagem. Este laço nos permite repetir uma ou mais instruções de código repetidamente, até que o comando return seja encontrado, o que faz com que o laço seja interrompido. Veja no trecho de código abaixo como podemos usar o laço loop da Common Lisp para contar e exibir os valores de 1 até 10:
(
; vamos declarar a variável que vamos usar
let (numero)
; vamos inicializar a variável com o valor 1
(setq numero 1)
; agora iniciamos o laço
(loop
; escrevemos o valor da variável
(write numero)
; aumentamos o valor da variável em 1
(setq numero (+ numero 1))
; provocamos uma quebra de linha
(terpri)
; e fazemos o teste da continuidade
(when (> numero 10) (return))
)
)
Ao executarmos este código Common Lisp nós teremos o seguinte resultado: 1 2 3 4 5 6 7 8 9 10 Veja que usamos a macro when para testar o ponto de parada do laço. Note ainda o uso da função terpri da Common Lisp para provocar uma quebra de linha na saída do programa. |
JavaScript ::: Dicas & Truques ::: Formulários |
Formulários HTML - Como marcar ou desmarcar todas as checkboxes de um formulário HTML de uma só vez usando JavaScriptQuantidade de visualizações: 19080 vezes |
|
Nesta dica mostrarei como é possível clicar em um botão (pode ser um link também) e chamar uma função JavaScript que marca ou desmarca todos os elementos HTML checkbox de uma só vez. Para isso usaremos o método getElementsByName() para retornar todas as checkbox e em seguida manipular sua propriedade checked. Veja a imagem abaixo: 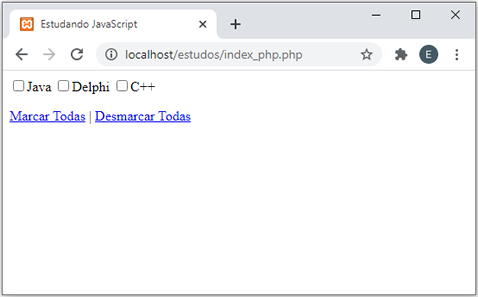 E agora o código HTML e JavaScript completo:
<html>
<head>
<title>Estudando JavaScript</title>
</head>
<body>
<form name="teste">
<input type="checkbox" name="linguagem">Java
<input type="checkbox" name="linguagem">Delphi
<input type="checkbox" name="linguagem">C++
</form>
<a href="javascript:marcar()">Marcar Todas</a> |
<a href="javascript:desmarcar()">Desmarcar Todas</a>
<script language="JavaScript">
function marcar(){
var boxes = document.getElementsByName("linguagem");
for(var i = 0; i < boxes.length; i++)
boxes[i].checked = true;
}
function desmarcar(){
var boxes = document.getElementsByName("linguagem");
for(var i = 0; i < boxes.length; i++)
boxes[i].checked = false;
}
</script>
</body>
</html>
|
Python ::: Python para Engenharia ::: Engenharia Civil - Concreto, Concreto Armado e Concretos Especiais |
Cálculo de estribos em vigas de concreto armado usando Python - Armadura mínima transversal normativaQuantidade de visualizações: 288 vezes |
|
A ABNT NBR 6118 (Projeto de estruturas de concreto armado) define uma taxa de armadura mínima para os estribos das vigas de concreto armado, e, a partir dessa taxa mínima nós podemos facilmente calcular a área de aço mínima a ser usada. A fórmula para o cálculo da taxa mínima de armadura tranversal pode ser definida como: \[\rho_\text{sw} = 0,2 \cdot \frac{f_\text{ck,m}}{f_\text{ywk}} \] Onde: ρsw é um número adimensional representando a taxa de armadura mínima transversal de acordo com recomendações da norma NBR 6118; fctk,m é a resistência à tração média do concreto em Mpa; fymk é a resistência à tração do aço em Mpa. Em geral, esse valor é fixado em 500 (CA 50), mesmo que o aço usado seja CA 60 ou superior; Após calculada a taxa de armadura transversal mínima, podemos calcular a área de aço mínima transversal por meio da seguinte fórmula: \[A_\text{sw,min} = \rho_\text{sw} \cdot b_w \cdot S \cdot sen(\alpha) \] Onde: Asw,min é a área de aço mínima a ser usada, em cm2/m; ρsw é um número adimensional representando a taxa de armadura mínima transversal de acordo com recomendações da norma NBR 6118; bw é a largura da viga em centímetros; S é o espaçamento a ser considerado. Informamos o valor de 100 para considerar um espaçamento de 1 metro; α é a inclinação dos estribos, em geral 90º. Veja agora o código Python :
# vamos importar o módulo Math
import math
# função principal do programa
def main():
# vamos pedir para o usuário informar o FCK do concreto
fck = float(input("Informe o FCK do concreto em Mpa: "))
# agora vamos calcular a resistência à tração média
# do concreto
fctk_m = 0.3 * math.pow(fck, 2.0 / 3.0)
# vamos pedir para o usuário informar a largura da viga em cm
largura = float(input("Informe a largura da viga em cm: "))
# vamos calcular a taxa de armadura transversal mínima
fywk = 500 # vamos considerar aço CA 50
psw = 0.2 * (fctk_m / fywk)
# agora vamos calcular a área mínima de aço para a armadura
# tranversal, ou seja, os estribos
S = 100 # considerando 1 metro de viga
inclinacao = 90 # inclinação em graus dos estribos
aws_min = psw * largura * S * math.sin(math.radians(inclinacao))
# e mostramos os resultados
print("\n-------RESULTADOS--------------------------------------")
print("A resistência à tração média do concreto é: {0} Mpa".
format(round(fctk_m, 5)))
print("A taxa de armadura transversal mínima é: {0}".format(
round(psw, 5)))
print("A área mínima de aço é: {0} cm2/m".format(round(aws_min, 5)))
if __name__ == "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Informe o FCK do concreto em Mpa: 25 Informe a largura da viga em cm: 19 -------RESULTADOS-------------------------------------- A resistência à tração média do concreto é: 2.56496 Mpa A taxa de armadura transversal mínima é: 0.00103 A área mínima de aço é: 1.94937 cm2/m |
GNU Octave ::: GNU Octave para Engenharia ::: Cálculo Diferencial e Integral |
Como calcular a derivada de uma função usando a função diff() do GNU Octave - Regra do Tombo (ou Regra da Potência)Quantidade de visualizações: 3762 vezes |
|
No cálculo, a derivada em um ponto de uma função y = f(x) representa a taxa de variação instantânea de y em relação a x neste ponto. Um exemplo típico é a função velocidade que representa a taxa de variação (derivada) da função espaço. Do mesmo modo, a função aceleração é a derivada da função velocidade. Geometricamente, a derivada no ponto x = a de y = f(x) representa a inclinação da reta tangente ao gráfico desta função no ponto (a,~f(a)). A função que a cada ponto x associa a derivada neste ponto de f(x) é chamada de função derivada de f(x). [Citação da Wikipédia] Nesta dica mostrarei como podemos usar a função diff() do GNU Octave para calcular a derivada de uma função usando a Regra do Tombo ou, mais formalmente, a Regra da Potência. Dada uma função:  A Regra do Tombo pede que o n desça e multiplique o x, que agora estará elevado a n - 1. Vamos ver um exemplo então? Observe como a derivada de f(x) = x5 é calculada na imagem a seguir:  Veja agora como podemos fazer este cálculo em GNU Octave. Para isso, abra a janela de comandos e dispare as linhas a seguir:
>> pkg load symbolic [ENTER]
>> syms x [ENTER]
>> f = x ** 5 [ENTER]
f = (sym)
5
x
>> diff(f, x) [ENTER]
ans = (sym)
4
5*x
>>
É possível que, após o comando "syms x" você veja algumas mensagens de aviso relacionadas à sua versão instalada do Python. Não se preocupe, pois esses avisos não interferem na funcionalidade da função diff(). |
Java ::: Dicas & Truques ::: Programação Orientada a Objetos |
Programação orientada a objetos em Java - Java OOP - Como usar variáveis estáticas em suas classes JavaQuantidade de visualizações: 12084 vezes |
|
Variáveis estáticas podem ser definidas em Java por meio do uso da palavra-chave static. Uma variável estática pertence à classe na qual ela é definida e não à cada uma de suas instâncias. Pareceu confuso? Você pode pensar assim: quando definida com o modificador static, uma variável será única na classe, não importa a quantidade de instâncias da classe que serão criadas. Cada uma destas instâncias compartilhará o valor da variável estática. Além disso, uma variável estática pode ser acessada por meio do nome da classe, sem a necessidade de uma referência a uma de suas instâncias. Uma variável estática pode ser public, private ou protected. Vamos ver um exemplo? Considere a situação na qual gostaríamos de criar um identificador único para cada um dos objetos de uma classe. Veja o código para a classe Livro: Código para Livro.java:
package estudos;
public class Livro {
// variáveis privadas
private String titulo; // título do livro
// variável estática que permitirá definir um
// identificador único para cada livro
private static int id;
// construtor da classe Livro
public Livro(){
// vamos incrementar a variável estática
Livro.id++;
}
// método que permite obter o id do livro
public int getId(){
return Livro.id;
}
// método que permite definir o título do livro
public void setTitulo(String titulo){
this.titulo = titulo;
}
// método que permite obter o título do livro
public String getTitulo(){
return this.titulo;
}
}
Veja agora como criar três objetos da classe Livro a partir do método main() da aplicação: Código para Main.java:
package estudos;
public class Main {
public static void main(String[] args) {
// vamos criar um objeto da classe Livro
Livro a = new Livro();
a.setTitulo("Programando em Java 2");
// vamos exibir os dados do livro
System.out.println("Id: " + a.getId());
System.out.println("Titulo: " + a.getTitulo());
// vamos criar mais um livro
Livro b = new Livro();
b.setTitulo("A biblia do C/C++");
// vamos exibir os dados do livro
System.out.println("Id: " + b.getId());
System.out.println("Titulo: " + b.getTitulo());
// e mais um livro aqui
Livro c = new Livro();
c.setTitulo("PHP + MySQL");
// vamos exibir os dados do livro
System.out.println("Id: " + c.getId());
System.out.println("Titulo: " + c.getTitulo());
}
}
Ao executar esta aplicação teremos o seguinte resultado: Id: 1 Titulo: Programando em Java 2 Id: 2 Titulo: A biblia do C/C++ Id: 3 Titulo: PHP + MySQL Como podemos ver, a cada instância criada a variável id é incrementada em 1. Caso você não tenha entendido todo o processo, este incremento acontece no construtor da classe Livro. Veja: // vamos incrementar a variável estática Livro.id++; Nas situações em que as variáveis estáticas são públicas, podemos acessá-la usando o nome da classe seguida de um ponto. Assim, se a variável id fosse pública, poderíamos acessá-la de qualquer lugar de nossa aplicação da seguinte forma: System.out.println(Livro.id); |
Dart ::: Dicas & Truques ::: Aplicativos e Outros |
Como calcular a distância entre dois pontos na terra em DartQuantidade de visualizações: 1708 vezes |
|
Nesta dica mostrarei como calcular a distância em quilômetros entre dois pontos na terra dadas suas latitudes e longitudes. Neste exemplo eu coloquei o valor de 6378.137 para o raio da terra, mas você pode definir para o valor que achar mais adequado. O cálculo usado neste código se baseia na Fórmula de Haversine, que determina a distância do grande círculo entre dois pontos em uma esfera, dadas suas longitudes e latitudes. Veja o código Dart completo:
// Vamos importar a biblioteca dart:io
import "dart:io";
// vamos importar a biblioteca dart:math
import "dart:math";
void main(){
// vamos ler as latitudes e longitudes das duas
// localizações
stdout.write("Informe a primeira latitude: ");
double lat1 = double.parse(stdin.readLineSync());
stdout.write("Informe a primeira longitude: ");
double lon1 = double.parse(stdin.readLineSync());
stdout.write("Informe a segunda latitude: ");
double lat2 = double.parse(stdin.readLineSync());
stdout.write("Informe a segunda longitude: ");
double lon2 = double.parse(stdin.readLineSync());
// vamos calcular a distância entre os dois pontos em Kms
double distancia = calcularDistancia(lat1, lat2, lon1, lon2);
// mostramos o resultado
print("Distância entre os dois pontos: ${distancia} kms");
}
// função que recebe dois pontos na terra e retorna a distância
// entre eles em quilômetros
double calcularDistancia(double lat1,
double lat2, double lon1, double lon2){
double raio_terra = 6378.137; // raio da terra em quilômetros
// o primeiro passo é converter as latitudes e longitudes
// para radianos
lon1 = grausParaRadianos(lon1);
lon2 = grausParaRadianos(lon2);
lat1 = grausParaRadianos(lat1);
lat2 = grausParaRadianos(lat2);
// agora aplicamos a Fórmula de Haversine
double dlon = lon2 - lon1;
double dlat = lat2 - lat1;
double a = pow(sin(dlat / 2), 2) + cos(lat1) * cos(lat2)
* pow(sin(dlon / 2),2);
double c = 2 * asin(sqrt(a));
// e retornamos a distância
return(c * raio_terra);
}
// função que permite converter graus em radianos
double grausParaRadianos(double graus){
return graus * (pi / 180);
}
Ao executar este código Dart nós teremos o seguinte resultado: Informe a primeira latitude: -16.674551 Informe a primeira longitude: -49.303598 Informe a segunda latitude: -15.579321 Informe a segunda longitude: -56.10009 A distância entre os dois pontos é: 736.9183827638687kms Neste exemplo eu calculei a distância entre as cidades de Goiânia-GO e Cuibá-MT. A latitude é a distância ao Equador medida ao longo do meridiano de Greenwich. Esta distância mede-se em graus, podendo variar entre 0o e 90o para Norte(N) ou para Sul(S). A longitude é a distância ao meridiano de Greenwich medida ao longo do Equador. |
C++ ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em C++ dados dois pontos no plano cartesianoQuantidade de visualizações: 1428 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem C++ que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
#include <iostream>
#include <cstdlib>
using namespace std;
int main(int argc, char *argv[]){
// coordenadas dos dois pontos
float x1, y1, x2, y2;
// guarda o coeficiente angular
float m;
// x e y do primeiro ponto
cout << "Coordenada x do primeiro ponto: ";
cin >> x1;
cout << "Coordenada y do primeiro ponto: ";
cin >> y1;
// x e y do segundo ponto
cout << "Coordenada x do segundo ponto: ";
cin >> x2;
cout << "Coordenada y do segundo ponto: ";
cin >> y2;
// vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1);
// mostramos o resultado
cout << "O coeficiente angular é: " << m << "\n\n";
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
Ao executar este código C++ nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.666667 Pressione qualquer tecla para continuar... Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
#include <iostream>
#include <cstdlib>
#include <math.h>
using namespace std;
int main(int argc, char *argv[]){
// coordenadas dos dois pontos
float x1, y1, x2, y2;
// guarda os comprimentos dos catetos oposto e adjascente
float cateto_oposto, cateto_adjascente;
// guarda o ângulo tetha (em radianos) e a tangente
float tetha, tangente;
// x e y do primeiro ponto
cout << "Coordenada x do primeiro ponto: ";
cin >> x1;
cout << "Coordenada y do primeiro ponto: ";
cin >> y1;
// x e y do segundo ponto
cout << "Coordenada x do segundo ponto: ";
cin >> x2;
cout << "Coordenada y do segundo ponto: ";
cin >> y2;
// vamos obter o comprimento do cateto oposto
cateto_oposto = y2 - y1;
// e agora o cateto adjascente
cateto_adjascente = x2 - x1;
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
tetha = atan2(cateto_oposto, cateto_adjascente);
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
tangente = tan(tetha);
// mostramos o resultado
cout << "O coeficiente angular é: " << tangente << "\n\n";
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Android Java ::: Gerenciadores de Layout ::: LinearLayout |
Como usar o gerenciador de layout LinearLayout em suas aplicações AndroidQuantidade de visualizações: 8096 vezes |
O gerenciador de layout LinearLayout (no pacote android.widget) do Android SDK nos permite exibir seus componentes filhos em uma única coluna ou linha. Esta classe está disponível desde a API Level 1. Veja sua posição na hierarquia de classes do Android:
java.lang.Object
android.view.View
android.view.ViewGroup
android.widget.LinearLayout
As classes diretas mais conhecidas são: NumberPicker, RadioGroup, SearchView, TabWidget, TableLayout, TableRow e ZoomControls. Veja um exemplo de como podemos usar o gerenciador LinearLayout em um arquivo de layout em XML:
<LinearLayout xmlns:android="http://schemas.android.com/apk/res/android"
android:orientation="vertical"
android:layout_width="fill_parent"
android:layout_height="fill_parent">
</LinearLayout>
Veja agora como este mesmo gerenciador pode ser criado em tempo de execução a partir do método onCreate() de uma activity:
package arquivo.estudos;
import android.app.Activity;
import android.os.Bundle;
import android.view.ViewGroup.LayoutParams;
import android.widget.LinearLayout;
public class EstudosActivity extends Activity
{
/** Called when the activity is first created. */
@Override
public void onCreate(Bundle savedInstanceState)
{
super.onCreate(savedInstanceState);
// vamos criar o gerenciador de layout
LinearLayout layout = new LinearLayout(this);
layout.setOrientation(LinearLayout.VERTICAL);
layout.setLayoutParams(new LinearLayout.LayoutParams(
LayoutParams.FILL_PARENT, LayoutParams.FILL_PARENT));
// vamos atribuir este layout à janela
setContentView(layout);
}
}
Em ambos os exemplos, os componentes filhos serão dispostos em uma única coluna, ou seja, serão empilhados na vertical, uma vez que o valor da orientação do layout é vertical. Note que a orientação do layout LinearLayout é definida em um arquivo XML usando o atributo android:orientation. Via código, a orientação é definida por meio de uma chamada ao método setOrientation(). A orientação padrão de um LinearLayout é horizontal (os componentes são dispostos em uma linha horizontal e a quebra de linha só ocorrerá quando forçada por questões de espaço). |
Nossas 20 dicas & truques de programação mais populares |
|
Java - Exercícios Resolvidos de Java - Como converter de binário para decimal em Java usando o laço for JavaScript - JavaScript Avançado - Como remover todas as ocorrências de uma substring em uma string usando uma função recursiva |
Você também poderá gostar das dicas e truques de programação abaixo |
|
C# - Como remover um elemento em uma determinada posição de uma List<T> do C# usando a função RemoveAt() |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




