 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
C# ::: Windows Forms ::: ListBox |
Como inserir um item em uma determinada posição da ListBox do C# Windows Forms usando o método Insert()Quantidade de visualizações: 948 vezes |
|
Em algumas situações nós gostaríamos de adicionar um novo item a uma ListBox do C# Windows Forms e indicar a posição (índice) na qual ela deverá ficar. Para isso podemos usar a função Insert() do objeto Items da ListBox. O método Insert() recebe o índice no qual o elemento será inserido e o item a ser inserido. Veja um exemplo de seu uso no trecho de código a seguir:
private void button2_Click(object sender, EventArgs e)
{
// insere um item na terceira posição
listBox1.Items.Insert(2, "Fortaleza");
}
Se o índice fornecido para o método Insert() não estiver dentro da faixa de índices válidos para os elementos da ListBox, uma exceção do tipo ArgumentOutOfRangeException será atirada: System.ArgumentOutOfRangeException HResult=0x80131502 Message=InvalidArgument=Value '20' não é um valor válido para 'index'. Parameter name: index Source=System.Windows.Forms StackTrace: em System.Windows.Forms.ListBox.ObjectCollection.Insert(Int32 index, Object item) |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Laços de Repetição |
Exercício Resolvido de Java - Usando o laço do...while para pedir ao usuário para informar números inteiros e calcular a quantidade de números positivos, negativos, a soma e a médiaQuantidade de visualizações: 9709 vezes |
|
Pergunta/Tarefa: Escreva um programa Java que usa o laço do...while para ler números inteiros até que o valor lido seja igual a 0. Em seguida mostre a quantidade de valores positivos e negativos, a soma dos valores e a média aritmética (sem incluir o valor 0 na contagem e no cálculo da média). A média deverá ser exibida como um valor de ponto flutuante. Sua saída deverá ser parecida com a mostrada abaixo: Informe um número inteiro (0 para sair): 5 Informe um número inteiro (0 para sair): -4 Informe um número inteiro (0 para sair): 3 Informe um número inteiro (0 para sair): 8 Informe um número inteiro (0 para sair): -2 Informe um número inteiro (0 para sair): 0 Quantidade de números positivos: 3 Quantidade de números negativos: 2 A soma dos números lidos é: 10 A média aritmética é: 2.0 Veja a resolução comentada deste exercício usando Java console:
package exercicios;
import java.util.Scanner;
public class Exercicios {
public static void main(String[] args) {
// vamos fazer a leitura usando a classe Scanner
Scanner entrada = new Scanner(System.in);
// declaração das variáveis
int numero, quantLidos = 0, soma = 0;
int quantPositivos = 0, quantNegativos = 0;
// laço do...while que repetirá até que o usuário informe o valor 0
do {
// lê o primeiro ou próximo número
System.out.print("Informe um número inteiro (0 para sair): ");
numero = Integer.parseInt(entrada.nextLine());
if(numero > 0){ // o número é positivo?
quantPositivos++;
}
else if(numero < 0){ // o número é negativo?
quantNegativos++;
}
// soma este número à soma já existente
soma += numero;
// aumenta a contagem dos números lidos
if(numero != 0){ // não incluir o 0 para sair do programa na contagem
quantLidos++;
}
}
while(numero != 0); // condição de parada do laço
if(quantLidos == 0){
System.out.println("Você não informou nenhum número.");
}
else{
System.out.println("Quantidade de números positivos: " + quantPositivos);
System.out.println("Quantidade de números negativos: " + quantNegativos);
System.out.println("A soma dos números lidos é: " + soma);
System.out.println("A média aritmética é: " + ((soma * 1.0) / quantLidos));
// note a multiplicação de soma por 1.0 para gerar um valor de ponto flutuante
// antes da divisão
}
}
}
|
Java ::: Dicas & Truques ::: Matemática e Estatística |
Como calcular juros simples e composto - Calculando juros simples e montante na linguagem JavaQuantidade de visualizações: 14485 vezes |
|
O regime de juros será simples quando o percentual de juros incidir apenas sobre o valor principal. Sobre os juros gerados a cada período não incidirão novos juros. Valor Principal, ou simplesmente principal, é o valor inicial emprestado ou aplicado, antes de somarmos os juros. Transformando em fórmula temos: J = P . i . n Onde: J = juros P = principal (capital) i = taxa de juros n = número de períodos Imaginemos uma dívida de R$ 2.000,00 que deverá ser paga com juros de 5% a.m. pelo regime de juros simples e o prazo para o pagamento é de 2 meses. O cálculo em Java pode ser feito assim:
public class Estudos{
public static void main(String args[]){
double principal = 2000.00;
double taxa = 0.08;
int meses = 2;
double juros = principal * taxa * meses;
System.out.println("O total de juros a ser pago é: "
+ juros);
System.exit(0);
}
}
O montante da dívida pode ser obtido das seguintes formas: a) Montante = Principal + Juros b) Montante = Principal + (Principal x Taxa de juros x Número de períodos) M = P . (1 + (i . n)) Veja o código:
public class Estudos{
public static void main(String args[]){
double principal = 2000.00;
double taxa = 0.08;
int meses = 2;
double juros = principal * taxa * meses;
double montante = principal * (1 + (taxa * meses));
System.out.println("O total de juros a ser pago é: "
+ juros);
System.out.println("O montante a ser pago é: "
+ montante);
System.exit(0);
}
}
|
JavaScript ::: Dicas & Truques ::: Cookies |
Cookies em JavaScript - Como obter o valor de um cookie usando JavaScriptQuantidade de visualizações: 215 vezes |
|
Nesta dica eu mostro como podemos escrever uma função JavaScript chamada obterCookie() que recebe o nome de um cookie e retorna o seu valor. Veja que, se o cookie com o nome informado não existir, o valor null é retornado. Veja o código JavaScript completo, incluindo o código HTML:
<html>
<head>
<title>Estudando JavaScript</title>
<script type="text/javascript">
// função que permite obter um cookie
function obterCookie(nome){
if(document.cookie.length > 0){
c_start = document.cookie.indexOf(nome + "=");
if(c_start != -1){
c_start = c_start + nome.length + 1;
c_end = document.cookie.indexOf(";", c_start);
if(c_end == -1){
c_end = document.cookie.length;
}
return unescape(document.cookie.substring(
c_start, c_end));
}
}
return null;
}
</script>
</head>
<body>
<script type="text/javascript">
// verifica se o cookie "nome_visitante" existe
// e obtém seu valor
var nome_visitante = obterCookie('nome_visitante');
if(nome_visitante != null){
document.writeln("O cookie nome_visitante existe. " +
"Seu valor é: " + nome_visitante);
}
else{
document.writeln("O cookie nome_visitante não existe");
}
</script>
</body>
</html>
Ao executar este código JavaScript nós teremos o seguinte resultado: O cookie nome_visitante existe. Seu valor é: Osmar |
GNU Octave ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em GNU Octave usando a função cos() - Calculadora de cosseno em OctaveQuantidade de visualizações: 2932 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da linguagem GNU Octave (script do GNU Octave). Esta função, já embutida na linguagem, recebe um valor numérico double e retorna um valor double, ou seja, também numérico) entre -1 até 1 (ambos inclusos). Veja:
# vamos calcular o cosseno de três números
fprintf("Cosseno de 0 = %f\n", cos(0))
fprintf("Cosseno de 1 = %f\n", cos(1))
fprintf("Cosseno de 2 = %f\n", cos(2))
Ao executar este código GNU Octave nós teremos o seguinte resultado: Cosseno de 0 = 1.000000 Cosseno de 1 = 0.540302 Cosseno de 2 = -0.416147 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 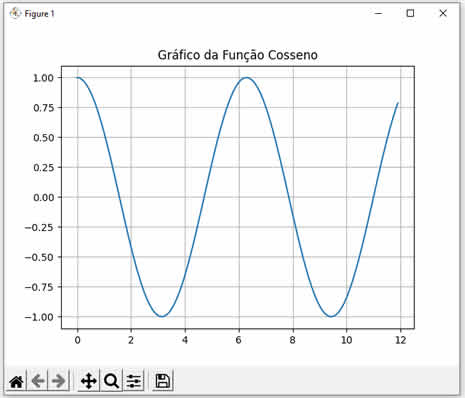 |
C ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular a área de um círculo em C dado o raio do círculoQuantidade de visualizações: 9057 vezes |
A área de um círculo pode ser calculada por meio do produto entre a constante PI e a medida do raio ao quadrado (r2). Comece analisando a figura abaixo: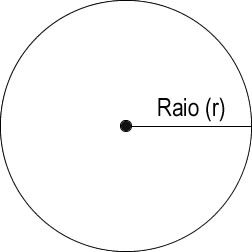 Sendo assim, temos a seguinte fórmula:  Onde A é a área, PI equivale a 3,14 (aproximadamente) e r é o raio do círculo. O raio é a medida que vai do centro até um ponto da extremidade do círculo. O diâmetro é a medida equivalente ao dobro da medida do raio, passando pelo centro do círculo e dividindo-o em duas partes. A medida do diâmetro é 2 * Raio. Veja agora um código C completo que calcula a área de um círculo mediante a informação do raio:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
// vamos definir o valor de PI
#define PI 3.14159265358979323846
int main(int argc, char *argv[]){
int raio;
printf("Informe o raio do círculo: ");
// efetua a leitura do raio
scanf("%d", &raio);
// calcula a área
double area = PI * pow(raio, 2);
// mostra o resultado
printf("A area do círculo de raio %d é igual a %f\n\n",
raio, area);
system("PAUSE");
return 0;
}
Ao executarmos este código nós teremos o seguinte resultado: Informe o raio do círculo: 5 A area do círculo de raio 5 é igual a 78.539816 A circunferência é um conjunto de pontos que estão a uma mesma distância do centro. Essa distância é conhecida como raio. A circunferência é estudada pela Geometria Analítica e, em geral, em um plano cartesiano. O círculo, que é formado pela circunferência e pelos infinitos pontos que preenchem seu interior, é estudado pela Geometria Plana, pois ele ocupa um espaço e pode ter sua área calculada, diferentemente da circunferência. |
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Recursão (Recursividade) |
Exercícios Resolvidos de Python - Uma função recursiva que conta quantas vezes um valor inteiro k ocorre em um vetor de inteirosQuantidade de visualizações: 650 vezes |
|
Pergunta/Tarefa: Escreva uma função recursiva em Python que conta quantas vezes um valor inteiro k ocorre em um vetor de 10 inteiros. Sua função deverá ter a seguinte assinatura: # função recursiva que recebe um valor e informa quantas vezes # ele aparece no vetor também informado def quant_repeticoes(indice, valor, vetor): # sua implementação aqui Sua saída deverá ser parecida com: Informe o 1 valor: 2 Informe o 2 valor: 7 Informe o 3 valor: 4 Informe o 4 valor: 7 Informe o 5 valor: 1 Informe o valor a ser pesquisado no vetor: 7 O valor informado se repete 2 vezes. Veja a resolução comentada deste exercício usando Python:
# método principal
def main():
# vamos declarar um vetor de 10 inteiros
valores = [0 for x in range(5)]
# vamos pedir ao usuário que informe os valores do vetor
for i in range(len(valores)):
valores[i] = int(input("Informe o %d.o valor: " % ((i + 1))))
# agora vamos pedir para informar o valor a ser pesquisado
valor = int(input("\nInforme o valor a ser pesquisado no vetor: "))
# e vamos ver a quantidade de repetições
repeticoes = quant_repeticoes(0, valor, valores)
print("O valor informado se repete {0} vezes.".format(repeticoes))
# função recursiva que recebe um valor e informa quantas vezes
# ele aparece no vetor também informado
def quant_repeticoes(indice, valor, vetor):
if indice == len(vetor) - 1: # caso base...hora de parar a recursividade
if vetor[indice] == valor:
return 1 # mais um repetição foi encontrada
else: # dispara mais uma chamada recursiva
if vetor[indice] == valor: # houve mais uma repetição
return 1 + quant_repeticoes(indice + 1, valor, vetor)
else:
return 0 + quant_repeticoes(indice + 1, valor, vetor) # não repetiu
return 0 # só para deixar o compilador satisfeito...esta linha nunca é executada
if __name__== "__main__":
main()
|
Java ::: Classes e Componentes ::: JTextArea |
Java Swing - Como adicionar mais texto a um JTextArea usando o método append()Quantidade de visualizações: 145 vezes |
|
Nesta dica mostrarei como é possível usar o método append() da classe JTextArea para adicionar mais conteúdo a esse controle. Esta é uma técnica muito importante no desenvolvimento de aplicações Java Swing. Segue um exemplo completo (note que fiz toda a aplicação Java Swing na mão mesmo, ou seja, não usei o editor visual do NetBeans ou semelhantes):
package arquivodecodigos;
import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
public class Estudos extends JFrame {
JTextArea textArea;
JTextField texto;
JButton btn;
public Estudos() {
super("Como adicionar texto a um JTextArea");
Container c = getContentPane();
FlowLayout layout = new FlowLayout(FlowLayout.LEFT);
c.setLayout(layout);
textArea = new JTextArea(10, 20);
texto = new JTextField(10);
btn = new JButton("Adicionar Texto");
btn.addActionListener(
new ActionListener() {
public void actionPerformed(ActionEvent e) {
textArea.append(texto.getText());
}
}
);
c.add(textArea);
c.add(texto);
c.add(btn);
setSize(350, 250);
setVisible(true);
}
public static void main(String args[]) {
Estudos app = new Estudos();
app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
}
Veja que neste exemplo, mais conteúdo é adicionado ao controle JTextArea sem provocar uma quebra de linha. Em outras dicas e truques dessa seção você aprenderá como isso pode ser feito. |
VB.NET ::: VB.NET para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular vetor unitário em VB.NET - VB.NET para Física e EngenhariaQuantidade de visualizações: 637 vezes |
|
Um vetor unitário ou versor num espaço vetorial normado é um vetor (mais comumente um vetor espacial) cujo comprimento ou magnitude é 1. Em geral um vetor unitário é representado por um "circunflexo", assim: __$\hat{i}__$. O vetor normalizado __$\hat{u}__$ de um vetor não zero __$\vec{u}__$ é o vetor unitário codirecional com __$\vec{u}__$. O termo vetor normalizado é algumas vezes utilizado simplesmente como sinônimo para vetor unitário. Dessa forma, o vetor unitário de um vetor __$\vec{u}__$ possui a mesma direção e sentido, mas magnitude 1. Por magnitude entendemos o módulo, a norma ou comprimento do vetor. Então, vejamos a fórmula para a obtenção do vetor unitário: \[\hat{u} = \dfrac{\vec{v}}{\left|\vec{v}\right|}\] Note que nós temos que dividir as componentes do vetor pelo seu módulo de forma a obter o seu vetor unitário. Por essa razão o vetor nulo não possui vetor unitário, pois o seu módulo é zero, e, como sabemos, uma divisão por zero não é possível. Veja agora o código VB.NET que pede as coordenadas x e y de um vetor 2D ou R2 e retorna o seu vetor unitário:
Imports System
Module Program
Sub Main(args As String())
' vamos ler os valores x e y
Console.Write("Informe o valor de x: ")
Dim x = Double.Parse(Console.ReadLine())
Console.Write("Informe o valor de y: ")
Dim y = Double.Parse(Console.ReadLine())
' o primeiro passo é calcular a norma do vetor
Dim norma = Math.Sqrt(Math.Pow(x, 2) + Math.Pow(y, 2))
' agora obtemos as componentes x e y do vetor unitário
Dim u_x = x / norma
Dim u_y = y / norma
' mostra o resultado
Console.WriteLine("O vetor unitário é: (x = " &
u_x & "; y = " & u_y)
Console.WriteLine(vbCrLf & "Pressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executar este código VB.NET nós teremos o seguinte resultado: Informe o valor de x: -4 Informe o valor de y: 6 O vetor unitário é: (x = -0.5547001962252291; y = 0.8320502943378437 Veja agora uma modificação deste código para retornarmos o vetor unitário de um vetor 3D ou R3, ou seja, um vetor no espaço:
Imports System
Module Program
Sub Main(args As String())
' vamos ler os valores x, y e z
Console.Write("Informe o valor de x: ")
Dim x = Double.Parse(Console.ReadLine())
Console.Write("Informe o valor de y: ")
Dim y = Double.Parse(Console.ReadLine())
Console.Write("Informe o valor de z: ")
Dim z = Double.Parse(Console.ReadLine())
' o primeiro passo é calcular a norma do vetor
Dim norma = Math.Sqrt(Math.Pow(x, 2) + Math.Pow(y, 2) +
Math.Pow(z, 2))
' agora obtemos as componentes x, y e z do vetor unitário
Dim u_x = x / norma
Dim u_y = y / norma
Dim u_z = z / norma
' mostra o resultado
Console.WriteLine("O vetor unitário é: (x = " &
u_x & "; y = " & u_y & "; z = " & u_z)
Console.WriteLine(vbCrLf & "Pressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Ao executarmos este novo código nós teremos o seguinte resultado: Informe o valor de x: 3 Informe o valor de y: 7 Informe o valor de z: 5 O vetor unitário é: (x = 0.329292779969071; y = 0.7683498199278324; z = 0.5488212999484517 |
Python ::: wxPython ::: Controles Visuais Básicos do wxPython |
Como usar a função GetDefaultSize() para obter o tamanho padrão dos botões wx.Button em uma determinada plataforma e um determinado tamanho de fonteQuantidade de visualizações: 6586 vezes |
|
Quando estamos escrevendo interfaces wxPython para múltiplas plataformas, é interessante usar o método GetDefaultSize() para obter as dimensões padrão dos botões. Isso permite que o próprio sistema determine o tamanho dos botões baseado no tamanho da fonte usada. Este método retorna um objeto da classe wx.Size e as dimensões podem ser obtidas com o auxílio das propriedades width (largura) e height (altura). Veja um exemplo wxPython completo:
# vamos importar a biblioteca wxPython
import wx
class Janela(wx.Frame):
def __init__(self):
wx.Frame.__init__(self, None, -1,
"Usando wx.Button", size=(350, 200))
# Cria um painel
panel = wx.Panel(self)
# Cria um botão e o adiciona no painel
self.btn = wx.Button(panel, label="Clique Aqui",
pos=(10, 10), size=(100, 25))
# Anexa um evento ao botão
self.Bind(wx.EVT_BUTTON, self.OnBtnClick, self.btn)
# Método que será chamado ao clicar o botão
def OnBtnClick(self, event):
# obtém o tamanho padrão dos botões
# nesta plataforma
dimensoes = self.btn.GetDefaultSize()
dlg = wx.MessageDialog(None, u"A largura padrão é: "
+ str(dimensoes.width) + u" pixels e a altura " +
u"padrão é: " + str(dimensoes.height) + " pixels",
"Usando wx.Button", wx.OK | wx.ICON_INFORMATION)
result = dlg.ShowModal()
dlg.Destroy()
if __name__ == "__main__":
app = wx.App()
janela = Janela()
janela.Show(True)
app.MainLoop()
|
Nossas 20 dicas & truques de programação mais populares |
|
Excel - Como gerar números aleatórios inteiros entre 1 e 10 no Excel usando as funções ALEATÓRIO() e INT() |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Java - Como percorrer uma árvore binária em Java usando o algorítmo depth-first search (DFS) recursivo C# - Como testar se uma string é null ou vazia em C# usando a função IsNullOrEmpty() da classe String |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




