 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
Delphi ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Delphi para iniciantes - Como escrever uma função que retorna uma matriz de IntegerQuantidade de visualizações: 13699 vezes |
Em algumas situações precisamos retornar uma matriz a partir de uma função. Nesta dica eu mostro como isso pode ser feito. O primeiro passo é declarar um novo tipo. Veja:type // vamos declarar um novo tipo TMatrizInteiros = array of Integer; Aqui o tipo TMatrizInteiros representa uma matriz de inteiros. Veja a unit completa para o exemplo:
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Memo1: TMemo;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
type // vamos declarar um novo tipo
TMatrizInteiros = array of Integer;
var
Form1: TForm1;
implementation
{$R *.dfm}
// função usada para construir e retornar uma
// matriz de Integer
function obterValores: TMatrizInteiros;
var
tempArray: TMatrizInteiros;
i: integer;
begin
// vamos definir o tamanho da matriz
SetLength(tempArray, 10);
// vamos inicializar a matriz com os números pares de 0 até 18
// note que em matrizes abertas o índice inicial é sempre 0
for i := Low(tempArray) to High(tempArray) do
begin
tempArray[i] := i * 2;
end;
Result := tempArray; // vamos retornar a matriz
end;
procedure TForm1.Button1Click(Sender: TObject);
var
valores: TMatrizInteiros; // uma matriz do tipo TMatrizInteiros
i: Integer;
begin
valores := obterValores();
// que já temos a matriz, vamos exibir os valores de
// seus elementos
for i := 0 to High(valores) do
begin
Memo1.Lines.Add(IntToStr(valores[i]));
end;
end;
end.
Note que a função retornará uma matriz aberta (open array). Desta forma, seu índice inicial será sempre 0. |
C++ ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como somar os elementos de um vetor de inteiros em C++Quantidade de visualizações: 17210 vezes |
Esta dica mostra a você como usar um laço for do C++ para somar todos os valores dos elementos de um vetor de inteiros. Observe que aqui nós declaramos e inicializamos o vetor (array) em apenas uma instrução:
#include <iostream>
using namespace std;
int main(int argc, char *argv[])
{
// declara e inicializa um array de
// 5 inteiros
int valores[] = {2, 7, 1, 5, 6};
int soma = 0;
// soma os valores dos elementos
for(int i = 0; i < 5; i++){
soma += valores[i];
// o mesmo que
// soma = soma + valores[i];
}
// exibe o resultado
cout << "Soma: " << soma << endl;
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
Ao executar este código C++ nós teremos o seguinte resultado: Soma: 21 |
Java ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em Java dados dois pontos no plano cartesianoQuantidade de visualizações: 1812 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem Java que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
package arquivodecodigos;
import java.util.Scanner;
public class Estudos{
public static void main(String args[]){
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// coordenadas dos dois pontos
double x1, y1, x2, y2;
// guarda o coeficiente angular
double m;
// x e y do primeiro ponto
System.out.print("Coordenada x do primeiro ponto: ");
x1 = Double.parseDouble(entrada.nextLine());
System.out.print("Coordenada y do primeiro ponto: ");
y1 = Double.parseDouble(entrada.nextLine());
// x e y do segundo ponto
System.out.print("Coordenada x do segundo ponto: ");
x2 = Double.parseDouble(entrada.nextLine());
System.out.print("Coordenada y do segundo ponto: ");
y2 = Double.parseDouble(entrada.nextLine());
// vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1);
// mostramos o resultado
System.out.println("O coeficiente angular é: " + m);
System.out.println("\n\n");
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.6666666666666666 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
package arquivodecodigos;
import java.util.Scanner;
public class Estudos{
public static void main(String args[]){
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// coordenadas dos dois pontos
double x1, y1, x2, y2;
// guarda os comprimentos dos catetos oposto e adjascente
double cateto_oposto, cateto_adjascente;
// guarda o ângulo tetha (em radianos) e a tangente
double tetha, tangente;
// x e y do primeiro ponto
System.out.print("Coordenada x do primeiro ponto: ");
x1 = Double.parseDouble(entrada.nextLine());
System.out.print("Coordenada y do primeiro ponto: ");
y1 = Double.parseDouble(entrada.nextLine());
// x e y do segundo ponto
System.out.print("Coordenada x do segundo ponto: ");
x2 = Double.parseDouble(entrada.nextLine());
System.out.print("Coordenada y do segundo ponto: ");
y2 = Double.parseDouble(entrada.nextLine());
// vamos obter o comprimento do cateto oposto
cateto_oposto = y2 - y1;
// e agora o cateto adjascente
cateto_adjascente = x2 - x1;
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
tetha = Math.atan2(cateto_oposto, cateto_adjascente);
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
tangente = Math.tan(tetha);
// mostramos o resultado
System.out.println("O coeficiente angular é: " + tangente);
System.out.println("\n\n");
System.exit(0);
}
}
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Ruby ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como somar os elementos da diagonal principal de uma matriz em RubyQuantidade de visualizações: 884 vezes |
|
A Matriz quadrada é um tipo especial de matriz que possui o mesmo número de linhas e o mesmo número de colunas, ou seja, dada uma matriz Anxm, ela será uma matriz quadrada se, e somente se, n = m, onde n é o número de linhas e m é o número de colunas. Em geral as matrizes quadradas são chamadas de Matrizes de Ordem n, onde n é o número de linhas e colunas. Dessa forma, uma matriz de ordem 4 é uma matriz que possui 4 linhas e quatro colunas. Toda matriz quadrada possui duas diagonais, e elas são muito exploradas tanto na matemática quanto na construção de algorítmos. Essas duas diagonais são chamadas de Diagonal Principal e Diagonal Secundária. A diagonal principal de uma matriz quadrada une o seu canto superior esquerdo ao canto inferior direito. Veja: 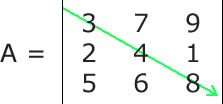 Nesta dica veremos como calcular a soma dos valores dos elementos da diagonal principal de uma matriz usando Ruby. Para isso, só precisamos manter em mente que a diagonal principal de uma matriz A é a coleção das entradas Aij em que i é igual a j. Assim, tudo que temos a fazer é converter essa regra para código Ruby. Veja um trecho de código Ruby completo no qual pedimos para o usuário informar os elementos da matriz e em seguida mostramos a soma dos elementos da diagonal superior:
# vamos declarar e construir uma matriz de três linhas e três colunas
matriz = Array.new(3){Array.new(3)}
soma_diagonal = 0; # guarda a soma dos elementos na diagonal principal
# vamos ler os valores para os elementos da matriz
for i in (0..2) # linhas
for j in (0..2) # colunas
printf("Valor para a linha %d e coluna %d: ", i, j)
matriz[i][j] = gets.chomp.to_i
end
end
# vamos mostrar a matriz da forma que ela
# foi informada
print("\n")
for i in (0..2) # linhas
for j in (0..2) # colunas
printf("%5d ", matriz[i][j])
end
print("\n")
end
# vamos calcular a soma dos elementos da diagonal
# principal
for i in (0..2) # linhas
for j in (0..2) # colunas
if(i == j)
soma_diagonal = soma_diagonal + matriz[i][j]
end
end
end
# e mostramos o resultado
printf("\nA soma dos elementos da diagonal principal é: %d",
soma_diagonal)
Ao executar este código Ruby nós teremos o seguinte resultado:
Informe o valor para a linha 0 e coluna 0: 3
Informe o valor para a linha 0 e coluna 1: 7
Informe o valor para a linha 0 e coluna 2: 9
Informe o valor para a linha 1 e coluna 0: 2
Informe o valor para a linha 1 e coluna 1: 4
Informe o valor para a linha 1 e coluna 2: 1
Informe o valor para a linha 2 e coluna 0: 5
Informe o valor para a linha 2 e coluna 1: 6
Informe o valor para a linha 2 e coluna 2: 8
3 7 9
2 4 1
5 6 8
A soma dos elementos da diagonal principal é: 15
|
GNU Octave ::: GNU Octave para Engenharia ::: Cálculo Diferencial e Integral |
Como calcular a derivada de uma função usando a função diff() do GNU Octave - Regra do Tombo (ou Regra da Potência)Quantidade de visualizações: 3756 vezes |
|
No cálculo, a derivada em um ponto de uma função y = f(x) representa a taxa de variação instantânea de y em relação a x neste ponto. Um exemplo típico é a função velocidade que representa a taxa de variação (derivada) da função espaço. Do mesmo modo, a função aceleração é a derivada da função velocidade. Geometricamente, a derivada no ponto x = a de y = f(x) representa a inclinação da reta tangente ao gráfico desta função no ponto (a,~f(a)). A função que a cada ponto x associa a derivada neste ponto de f(x) é chamada de função derivada de f(x). [Citação da Wikipédia] Nesta dica mostrarei como podemos usar a função diff() do GNU Octave para calcular a derivada de uma função usando a Regra do Tombo ou, mais formalmente, a Regra da Potência. Dada uma função:  A Regra do Tombo pede que o n desça e multiplique o x, que agora estará elevado a n - 1. Vamos ver um exemplo então? Observe como a derivada de f(x) = x5 é calculada na imagem a seguir:  Veja agora como podemos fazer este cálculo em GNU Octave. Para isso, abra a janela de comandos e dispare as linhas a seguir:
>> pkg load symbolic [ENTER]
>> syms x [ENTER]
>> f = x ** 5 [ENTER]
f = (sym)
5
x
>> diff(f, x) [ENTER]
ans = (sym)
4
5*x
>>
É possível que, após o comando "syms x" você veja algumas mensagens de aviso relacionadas à sua versão instalada do Python. Não se preocupe, pois esses avisos não interferem na funcionalidade da função diff(). |
Python ::: Dicas & Truques ::: Strings e Caracteres |
Como substituir partes de uma palavra, frase ou texto em Python usando a função replace() do objeto StringQuantidade de visualizações: 1896 vezes |
Em várias ocasiões nós precisamos efetuar a substituição de substrings em uma string. Para isso nós podemos usar o método replace() da linguagem Python. Esta função possui a seguinte assinatura:string.replace(oldvalue, newvalue, count) onde oldvalue é trecho da string a ser substituído, newvalue é o valor que substituirá o valor antigo e count é a quantidade de substituições. Na ausência do terceiro argumento, TODAS as ocorrências da substring pesquisada serão substituídas. Veja um exemplo no qual substituímos todas as ocorrências de "Java" por "Python" em uma frase:
def main():
# frase original
original = "Gosto de Java porque Java é fácil"
print("Frase original:", original)
# vamos substituir "Java" por "Python"
nova_frase = original.replace("Java", "Python")
print("Após a substituição:", nova_frase)
if __name__== "__main__":
main()
Ao executarmos este código Python nós teremos o seguinte resultado: Frase original: Gosto de Java porque Java é fácil Após a substituição: Gosto de Python porque Python é fácil |
PHP ::: Dicas & Truques ::: Data e Hora |
PHP para iniciantes - Como obter o número de dias em um mês e ano usando a função cal_days_in_month() do PHPQuantidade de visualizações: 86 vezes |
|
Em algumas situações nós precisamos saber quantos dias um determinado mês possui, talvez para exibir um calendário. Para isso nós podemos usar a função cal_days_in_month() da linguagem PHP. Esta função pede um tipo de calendário (geralmente CAL_GREGORIAN), um número indicando o mês (1 para janeiro, 2 para fevereiro, etc) e o ano). Veja o código completo para obter a quantidade de dias para o mês de fevereiro de 2021:
<?php
$ano = 2021;
$mes = 2; // fevereiro
$quant_dias = cal_days_in_month(CAL_GREGORIAN,
$mes, $ano);
echo "Há $quant_dias dias no mês e ano informados";
?>
Ao executarmos este código nós teremos o seguinte resultado: Há 28 dias no mês e ano informados |
Java ::: Coleções (Collections) ::: HashMap |
Como retornar a quantidade de mapeamentos (chave-valor) em um HashMap do Java usando o método size()Quantidade de visualizações: 8011 vezes |
Em algumas situações precisamos saber a quantidade de mapeamentos (chave-valor) contidos em um HashMap. Para isso nós podemos usar o método size(). Veja o exemplo:
import java.util.*;
public class Estudos{
public static void main(String[] args){
// vamos criar uma instância de HashMap
HashMap<Integer, String> clientes = new HashMap<Integer, String>();
// vamos adicionar três chaves e seus valores
clientes.put(new Integer(1), "Osmar J. Silva");
clientes.put(new Integer(2), "Salvador Miranda de Andrade");
clientes.put(new Integer(3), "Marcos da Costa Santos");
// vamos obter a quantidade de mapeamentos neste HashMap
int quant = clientes.size();
// vamos exibir o resultado
System.out.println("Este HashMap contém " + quant +
" mapeamentos.");
System.exit(0);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Este HashMap contém 3 mapeamentos. |
VisuAlg ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em VisuAlg dados dois pontos no plano cartesianoQuantidade de visualizações: 639 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem VisuAlg que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
algoritmo "Calcular o coeficiente angular de uma reta em VisuAlg"
var
// coordenadas dos dois pontos
x1, y1, x2, y2: real
// guarda o coeficiente angular
m: real
inicio
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos calcular o coeficiente angular
m <- (y2 - y1) / (x2 - x1)
// mostramos o resultado
escreva("O coeficiente angular é: ", m)
fimalgoritmo
Ao executar este código VisuAlg nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.6666666666666666 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
algoritmo "Calcular o coeficiente angular de uma reta em VisuAlg"
var
// coordenadas dos dois pontos
x1, y1, x2, y2: real
// guarda os comprimentos dos catetos oposto e adjascente
cateto_oposto, cateto_adjascente: real
// guarda o ângulo tetha (em radianos) e a tangente
tetha, tangente: real
inicio
// x e y do primeiro ponto
escreva("Coordenada x do primeiro ponto: ")
leia(x1)
escreva("Coordenada y do primeiro ponto: ")
leia(y1)
// x e y do segundo ponto
escreva("Coordenada x do segundo ponto: ")
leia(x2)
escreva("Coordenada y do segundo ponto: ")
leia(y2)
// vamos obter o comprimento do cateto oposto
cateto_oposto <- y2 - y1
// e agora o cateto adjascente
cateto_adjascente <- x2 - x1
// vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
// (em radianos, não se esqueça)
tetha <- ArcTan(cateto_oposto / cateto_adjascente)
// e finalmente usamos a tangente desse ângulo para calcular
// o coeficiente angular
tangente <- Tan(tetha)
// mostramos o resultado
escreva("O coeficiente angular é: ", tangente)
fimalgoritmo
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
C# ::: Dicas & Truques ::: Programação Orientada a Objetos |
Como criar sua primeira classe em C# - Programação Orientada a Objetos em C#Quantidade de visualizações: 34907 vezes |
|
O estudo da programação orientada a objeto em C# passa obrigatoriamente pela criação de sua primeira classe. E esta não é uma tarefa fácil para os iniciantes. Esta dica o guiará passo-a-passo pelas caminhos iniciais. Esta dica assume que você já sabe criar uma aplicação console ou Windows Forms no Visual C# 2005 ou 2008. Sendo assim, crie uma nova aplicação console e vamos criar o esqueleto da classe. Em Visual C# 2005 ou 2008, a forma mais comum de adicionar uma classe ao seu projeto é clicando com o botão direito no namespace do projeto (o primeiro filho do solution explorer) e escolhendo a opção Add -> Class. Em seguida dê o nome "Pessoa.cs" para a classe e clique o botão Add. Imediatamente o código inicial para a classe será exibido, contendo o namespace e alguns using padrões. Agora faça sua classe Pessoa parecida com o código abaixo (não altere nada em relação ao namespace):
class Pessoa{
// varíáveis privadas para o nome
// e idade da pessoa
private string nome;
private int idade;
// método que permite definir o nome
// da pessoa
public void setNome(string nome){
this.nome = nome;
}
// método que permite definir a idade
// da pessoa
public void setIdade(int idade){
this.idade = idade;
}
// método que permite obter o nome
// da pessoa
public string getNome(){
return this.nome;
}
// método que permite obter a idade
// da pessoa
public int getIdade(){
return this.idade;
}
}
Hora de testar a classe. Volte à classe principal da aplicação (aquela que contém o método Main) e faça as seguintes alterações:
static void Main(string[] args){
// Cria uma instância da classe Pessoa
Pessoa p = new Pessoa();
// Define um nome e idade para a pessoa
p.setNome("Osmar J. Silva");
p.setIdade(37);
// Obtém o nome e idade da pessoa
string nome = p.getNome();
int idade = p.getIdade();
Console.WriteLine("Nome: " + nome + " - Idade: " +
idade);
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
Funcionou? Agora tente refazer todo o processo, desta vez usando Windows Forms. |
Nossas 20 dicas & truques de programação mais populares |
|
VB.NET - Como comparar strings em VB.NET usando o método Equals() da classe String do .NET Framework |
Você também poderá gostar das dicas e truques de programação abaixo |
|
JavaScript - Como adicionar um método isPar() ao objeto Number do JavaScript que indicará se um número é par ou impar Revit C# - Como criar eixos no Revit via programação usando a função Create() da classe Grid da Revit C# API Delphi - Como obter e exibir todos os itens selecionados em uma TListBox do Delphi de seleção múltipla Java - Como usar null em Java |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




