 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
Ruby ::: Dicas & Truques ::: Strings e Caracteres |
Como concatenar strings em Ruby usando o operador <<Quantidade de visualizações: 8471 vezes |
Esta dica mostra como podemos usar o operador << para concatenar strings em Ruby. Veja: frase1 = "Gosto muito de Ruby" frase2 = " e de Python" # vamos concatenar as duas strings res = frase1 << frase2 # exibe o resultado puts res Ao executar este código Ruby nós teremos o seguinte resultado: Gosto muito de Ruby e de Python |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Laços de Repetição |
Exercícios Resolvidos de Java - Como converter decimal em binário em Java usando o laço whileQuantidade de visualizações: 6873 vezes |
|
Pergunta/Tarefa: Escreva um programa Java que usa o laço while para converter um número decimal em sua representação binária. Peça ao usuário para informar um número inteiro e mostre o mesmo em binário (como uma String). Você deve obrigatoriamente usar o laço while. Sua saída deverá ser parecida com: Informe um número decimal: 38 A representação binária é 100110 Veja a resolução comentada deste exercício usando Java:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
// vamos fazer a leitura usando a classe Scanner
Scanner entrada = new Scanner(System.in);
// vamos ler o número decimal
System.out.print("Informe um número decimal: ");
int decimal = Integer.parseInt(entrada.nextLine());
int decimal_temp = decimal; // para mostrar o resultado no final
String binario = ""; // vai guardar o resultado
int temp; // variável auxiliar
// laço while repetirá enquanto decimal for maior ou igual a 2
while(decimal >= 2){
temp = decimal % 2;
binario = temp + binario;
decimal = decimal / 2;
}
binario = decimal + binario; // insere o dígito 1 restante
System.out.println("A representação binária é " + binario);
}
}
|
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Python Básico |
Exercício Resolvido de Python - Como calcular o restante de um salário após o pagamento de duas contas com jurosQuantidade de visualizações: 1441 vezes |
|
Pergunta/Tarefa: Cintia acaba de receber seu salário mas precisa pagar duas contas atrasadas. Por causa do atraso, ela deverá pagar multa de 2% sobre cada conta. Faça um programa que leia o valor do salário e das duas contas e que calcule e mostre quanto restará do salário de Cintia. Sua saída deverá ser parecida com: Informe o salário: 1350 Valor da primeira conta: 140 Valor da segunda conta: 300 Total das contas sem juros: 440.0 Total dos juros: 8.8 Total das contas com juros: 448.8 Sobra do salário: 901.2 Veja a resolução comentada deste exercício usando Python:
# método principal
def main():
# vamos pedir que o usuário informe o valor do salário e das duas contas
salario = float(input("Informe o salário: "))
conta1 = float(input("Valor da primeira conta: "))
conta2 = float(input("Valor da segunda conta: "))
# total a ser pago nas duas contas sem os juros
total_contas = conta1 + conta2
# calcula os juros
total_juros = total_contas * 0.02
# total a ser pago com juros
total_contas_com_juros = total_contas + total_juros
# sobra do salário
sobra_salario = salario - total_contas_com_juros
# mostra os resultados
print("\nTotal das contas sem juros: {0}".format(total_contas))
print("Total dos juros: {0}".format(total_juros))
print("Total das contas com juros: {0}".format(total_contas_com_juros))
print("Sobra do salário: {0}".format(sobra_salario))
if __name__== "__main__":
main()
|
JavaScript ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em JavaScript usando a função cos() do objeto Math - Calculadora de cosseno em JavaScriptQuantidade de visualizações: 7631 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da linguagem JavaScript. Esta função, que é parte do objeto Math, recebe um valor numérico e retorna um valor também numérico) entre -1 até 1 (ambos inclusos). Veja:
<html>
<head>
<title>Estudos JavaScript</title>
</head>
<body>
<script type="text/javascript">
// vamos calcular o cosseno de 3 números
document.writeln("Cosseno de 0 = " + Math.cos(0));
document.writeln("<br>Cosseno de 1 = " + Math.cos(1));
document.writeln("<br>Cosseno de 2 = " + Math.cos(2));
</script>
</body>
</html>
Ao executar este código JavaScript nós teremos o seguinte resultado: Cosseno de 0 = 1 Cosseno de 1 = 0.5403023058681398 Cosseno de 2 = -0.4161468365471424 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 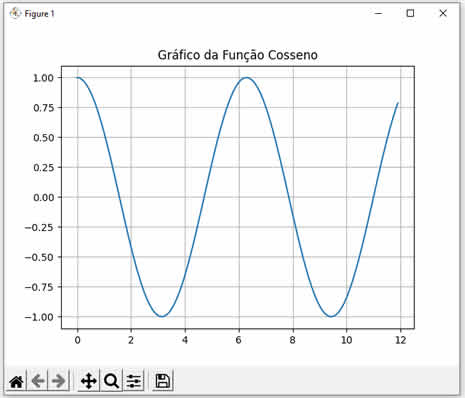 |
HTML5 ::: HTML5 + JavaScript ::: Canvas |
Programação gráfica para iniciantes - Como desenhar círculos com ou sem preenchimento usando o método arc() do objeto Canvas do HTML5Quantidade de visualizações: 6911 vezes |
Podemos usar o método arc() do objeto Canvas do HTML5 para desenhar círculos com ou sem prenchimento. Veja nos exemplos abaixo como isso pode ser feito. Primeiro um círculo sem preenchimento:
<!doctype html>
<html>
<head>
<title>O objeto Canvas do HTML5</title>
</head>
<body>
<Canvas id="canvas1" width="500" height="350"></Canvas>
<script type="text/javascript">
// obtemos uma referência ao elemento Canvas
var canvas = document.getElementById("canvas1");
// obtemos o contexto de desenho
var contexto = canvas.getContext("2d");
// vamos desenhar um círculo sem preenchimento com raio de 80
contexto.beginPath(); // início um novo caminho
// o círculo começa no x = 100, y = 100, começa no ângulo 0
// e vai até o ângulo 360 (as medidas são em radianos, não em graus)
contexto.arc(100, 100, 80, 0, 2 * Math.PI, false);
contexto.lineWidth = 2; // largura da linha
contexto.strokeStyle = '#990000'; // cor da linha
contexto.stroke(); // realiza o desenho
</script>
</body>
</html>
Ao abrir esta página HTML nós teremos o seguinte resultado:  E agora um círculo preenchido:
<!doctype html>
<html>
<head>
<title>O objeto Canvas do HTML5</title>
</head>
<body>
<Canvas id="canvas1" width="500" height="350"></Canvas>
<script type="text/javascript">
// obtemos uma referência ao elemento Canvas
var canvas = document.getElementById("canvas1");
// obtemos o contexto de desenho
var contexto = canvas.getContext("2d");
// vamos desenhar um círculo sem preenchimento com raio de 80
contexto.beginPath(); // início um novo caminho
// o círculo começa no x = 100, y = 100, começa no ângulo 0
// e vai até o ângulo 360 (as medidas são em radianos, não em graus)
contexto.arc(100, 100, 80, 0, 2 * Math.PI, false);
// vamos preencher o círculo
contexto.fillStyle = "#CCCCCC"; // cor do preenchimento
contexto.fill(); // preenche de fato
contexto.lineWidth = 2; // largura da linha
contexto.strokeStyle = '#990000'; // cor da linha
contexto.stroke(); // realiza o desenho
</script>
</body>
</html>
Ao abrir esta página HTML nós teremos o seguinte resultado:  |
Java ::: Dicas & Truques ::: Expressões Regulares |
Java Expressões Regulares - Como substituir todas as ocorrências de uma substring em uma string usando expressões regularesQuantidade de visualizações: 9359 vezes |
|
Este exemplo mostra como substituir todas as ocorrências de uma substring em uma string usando expressões regulares na linguagem Java. Nesta dica nós substituimos todas as ocorrências de "Java" por "C++". Veja o código completo:
package arquivodecodigos;
import java.util.regex.*;
public class Estudos{
public static void main(String args[]){
String padrao = "Java";
Pattern regPat = Pattern.compile(padrao);
String frase = "Java? Gosto muito de Java.";
System.out.println("Frase original: " + frase);
Matcher matcher = regPat.matcher(frase);
String res = matcher.replaceAll("C++");
System.out.println("Depois da substituição: " + res);
}
}
Ao executarmos este código Java nós teremos o seguinte resultado: Frase original: Java? Gosto muito de Java. Depois da substituição: C++? Gosto muito de C++. |
GNU Octave ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em GNU Octave dados dois pontos no plano cartesianoQuantidade de visualizações: 1582 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem GNU Octave (script GNU Octave) que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
# x e y do primeiro ponto
x1 = input("Coordenada x do primeiro ponto: ")
y1 = input("Coordenada y do primeiro ponto: ")
# x e y do segundo ponto
x2 = input("Coordenada x do segundo ponto: ")
y2 = input("Coordenada y do segundo ponto: ")
# agora vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1)
# mostramos o resultado
fprintf("O coeficiente angular é: %f\n\n", m)
Ao executar este código em linguagem GNU Octave nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 x1 = 3 Coordenada y do primeiro ponto: 6 y1 = 6 Coordenada x do segundo ponto: 9 x2 = 9 Coordenada y do segundo ponto: 10 y2 = 10 m = 0.6667 O coeficiente angular é: 0.666667 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
# x e y do primeiro ponto
x1 = input("Coordenada x do primeiro ponto: ")
y1 = input("Coordenada y do primeiro ponto: ")
# x e y do segundo ponto
x2 = input("Coordenada x do segundo ponto: ")
y2 = input("Coordenada y do segundo ponto: ")
# vamos obter o comprimento do cateto oposto
cateto_oposto = y2 - y1
# e agora o cateto adjascente
cateto_adjascente = x2 - x1
# vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
# (em radianos, não se esqueça)
tetha = atan2(cateto_oposto, cateto_adjascente)
# e finalmente usamos a tangente desse ângulo para calcular
# o coeficiente angular
tangente = tan(tetha)
# mostramos o resultado
fprintf("O coeficiente angular é: %f\n\n", tangente)
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
C# ::: Dicas & Truques ::: Matemática e Estatística |
Como gerar um número aleatório usando a função Next() da classe Random do C#Quantidade de visualizações: 23904 vezes |
|
Este exemplo mostra como gerar números randômicos usando C#. Para isso nós vamos usar o método Next() da classe Random. Este método retorna um número inteiro maior ou igual a zero e menor que a constante MaxValue (cujo valor é 2.147.483.647). Observe que cada chamada a Next() gera um número aleatório diferente, não havendo a necessidade de criar um novo objeto da classe Random para cada número desejado. Eis o código:
static void Main(string[] args){
// cria um objeto da classe Random
Random rnd = new Random();
// gera o número aleatório na faixa
// 0 até MaxValue (2.147.483.647)
int numero = rnd.Next();
// exibe o resultado
Console.Write("O número gerado foi: {0}", numero);
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
Ao executar este código C# nós teremos o seguinte resultado: O número gerado foi: 504 |
C# ::: Desafios e Lista de Exercícios Resolvidos ::: Matemática e Estatística |
Exercícios Resolvidos de C# - Como calcular juros simples em C# - Um programa C# que lê o valor principal, o tempoQuantidade de visualizações: 737 vezes |
|
Pergunta/Tarefa: Saber como escrever um programa C# que recebe o valor principal, o tempo e a taxa de juros e retorna os juros simples a serem pagos ou recebidos é uma habilidade que todo programador deve aprender em algum ponto de sua carreira. Sendo assim, escreva um algoritmo em C# que pede para o usuário informar um valor a ser pago ou recebido, o tempo em dias, meses ou anos e a taxa de juros (sem dividi-la por 100) e retorne os juros simples a serem pagos ou recebidos. Note que, se você quiser mostrar o valor total a ser pago ou recebido, basta somar os juros ao valor principal. Antes, porém, veja a fórmula do cálculo de juros simples: \[\text{Juros} = \frac{\text{C} \times \text{i} \times \text{t}}{100}\] Onde: C é o valor a ser pago ou a ser recebido; i é a taxa de juros (sem dividir por 100); t é o tempo em dias, meses, anos, etc. Sua saída deverá ser parecida com: Informe o valor principal: 600 Taxa de juros: 12 Informe o tempo: 5 Juros a serem pagos ou recebidos: 360.0 Veja a resolução comentada deste exercício usando C#:
using System;
namespace Estudos {
class Principal {
// função principal do programa C#
static void Main(string[] args) {
// vamos ler o valor principal
Console.Write("Informe o valor principal: ");
double principal = Double.Parse(Console.ReadLine());
// agora vamos ler a taxa de juros
Console.Write("Taxa de juros: ");
double taxa = Double.Parse(Console.ReadLine());
// finalmente o tempo em dias, meses, anos, etc
Console.Write("Informe o tempo: ");
int tempo = Int32.Parse(Console.ReadLine());
// vamos calcular os juros
double juros = (principal * taxa * tempo) / 100;
// e mostramos o resultado
Console.WriteLine("Juros a serem pagos ou recebidos: " + juros);
Console.WriteLine("\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
|
Python ::: Dicas & Truques ::: Sistema |
Como obter o diretório do seu programa Python usando sys.path[0]Quantidade de visualizações: 9936 vezes |
|
Nesta dica eu mostrarei como é possível usar a primeira posição da lista de strings contida na propriedade path do módulo sys da linguagem Python. Lembre-se de que sys.path contém uma lista de strings especificando os caminhos de busca para os módulos Python. Veja o código completo para o exemplo:
import sys
# função principal do programa
def main():
print("O diretório do programa é: ", sys.path[0])
if __name__== "__main__":
main()
Ao executarmos este código nós teremos o seguinte resultado: O diretório do programa é: c:\estudos_python |
Nossas 20 dicas & truques de programação mais populares |
|
wxWidgets - Como baixar, compilar a biblioteca e criar um projeto C++ wxWidgets usando o Visual Studio 2017 |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Delphi - Como obter o número do registro atual em um TClientDataSet do Delphi usando a propriedade RecNo |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





