 |
|
||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
C# ::: Coleções (Collections) ::: List<T> |
Como pesquisar um elemento em uma lista do C# usando a função Find() e um PredicateQuantidade de visualizações: 15149 vezes |
|
Em algumas situações gostaríamos de pesquisar e retornar o primeiro elemento de uma List<T> que obedece a algum critério de busca. Assim, poderíamos, por exemplo, pesquisar um nome que começa com uma determinada palavra ou um preço de produto maior ou igual a um determinado valor. Para tais situações podemos usar o método Find(). Este método possui a seguinte assinatura: public T Find( Predicate<T> match ) Veja que o método pede um delegate do tipo Predicate<T> que define as condições para a pesquisa do elemento. Se o elemento for encontrado, este é retornado. Caso contrário, o valor padrão para T é retornado (null para referências). Veja um trecho de código no qual eu mostro como usar o método Find() em combinação com um método personalizado que permite usar um delegate anônimo. Desta forma conseguimos fornecer, em tempo de execução, o argumento para o parâmetro match do Predicate:
static void Main(string[] args){
// vamos criar um objeto da classe List<T>
List<string> nomes = new List<string>();
// vamos inserir quatro valores na lista
nomes.Add("Osmar J. Silva");
nomes.Add("Salvador Miranda de Andrade");
nomes.Add("Dyego Fernandes de Souza");
nomes.Add("Marcos de Paula Rocha");
// vamos pesquisar um valor na lista usando um método personalizado
// Neste exemplo vamos retornar o primeiro nome que contenha a palavra
// "Dyego"
string nome = encontrar(nomes, "Dyego");
// vamos verificar se o nome foi encontrado
if(nome != null){
// foi encontrado....vamos retornar o resultado
Console.WriteLine(nome);
}
else{
Console.WriteLine("Nenhum nome encontrado.");
}
// vamos pausar a execução
Console.Write("\n\nPressione qualquer tecla para continuar...");
Console.ReadKey();
}
// método auxiliar que permite encontrar um valor na lista usando
// o método Find() da classe List<T> e um Predicate
static string encontrar(List<string> lista, string texto){
string encontrado = null;
// vamos pesquisar o valor na lista usando seu método Find()
// Aqui o primeiro nome que passar no critério de busca será retornado
encontrado = lista.Find(delegate(string valor){
return valor.Contains(texto);
});
return encontrado;
}
O método Find() executa uma busca linear. Assim, este método é uma operação O(n), onde n é a quantidade de elementos na lista. |
Java ::: Estruturas de Dados ::: Árvore Binária e Árvore Binária de Busca |
Estruturas de dados em Java - Como pesquisar um nó em uma árvore binária de busca usando um método recursivo usando JavaQuantidade de visualizações: 2550 vezes |
|
Nesta dica mostraremos um exemplo completo de como pesquisar um valor em uma árvore binária de busca em Java. Note que o exemplo usa apenas inteiros, mas você não terá dificuldades para modificar a classe Nó para os dados que você precisar. Código para No.java:
package arvore_binaria;
public class No {
private int valor; // valor armazenado no nó
private No esquerdo; // filho esquerdo
private No direito; // filho direito
// construtor do nó
public No(int valor){
this.valor = valor;
this.esquerdo = null;
this.direito = null;
}
public int getValor() {
return valor;
}
public void setValor(int valor) {
this.valor = valor;
}
public No getEsquerdo() {
return esquerdo;
}
public void setEsquerdo(No esquerdo) {
this.esquerdo = esquerdo;
}
public No getDireito() {
return direito;
}
public void setDireito(No direito) {
this.direito = direito;
}
}
Código para ArvoreBinariaBusca.java:
package arvore_binaria;
public class ArvoreBinariaBusca {
private No raiz; // referência para a raiz da árvore
// método usado para inserir um novo nó na árvore
// retorna true se o nó for inserido com sucesso e false
// se o elemento
// não puder ser inserido (no caso de já existir um
// elemento igual)
public boolean inserir(int valor){
// a árvore ainda está vazia?
if(raiz == null){
// vamos criar o primeiro nó e definí-lo como a raiz da árvore
raiz = new No(valor); // cria um novo nó
}
else{
// localiza o nó pai do novo nó
No pai = null;
No noAtual = raiz; // começa a busca pela raiz
// enquanto o nó atual for diferente de null
while(noAtual != null){
// o valor sendo inserido é menor que o nó atual?
if(valor < noAtual.getValor()) {
pai = noAtual;
// vamos inserir do lado esquerdo
noAtual = noAtual.getEsquerdo();
}
// o valor sendo inserido é maior que o nó atual
else if(valor > noAtual.getValor()){
pai = noAtual;
// vamos inserir do lado direito
noAtual = noAtual.getDireito();
}
else{
return false; // um nó com este valor foi encontrado
}
}
// cria o novo nó e o adiciona como filho do nó pai
if(valor < pai.getValor()){
pai.setEsquerdo(new No(valor));
}
else{
pai.setDireito(new No(valor));
}
}
return true; // retorna true para indicar que o novo nó foi inserido
}
// método que permite pesquisar na árvore binária de busca
public No pesquisar(int valor){
return pesquisar(raiz, valor); // chama a versão recursiva do método
}
// sobrecarga do método pesquisar que recebe dois
// parâmetros (esta é a versão recursiva do método)
private No pesquisar(No noAtual, int valor){
// o valor pesquisado não foi encontrado....vamos retornar null
if(noAtual == null){
return null;
}
// o valor pesquisado foi encontrado?
if(valor == noAtual.getValor()){
return noAtual; // retorna o nó atual
}
// ainda não encontramos...vamos disparar uma nova
// chamada para a sub-árvore da esquerda
else if(valor < noAtual.getValor()){
return pesquisar(noAtual.getEsquerdo(), valor);
}
// ainda não encontramos...vamos disparar uma nova
// chamada para a sub-árvore da direita
else{
return pesquisar(noAtual.getDireito(), valor);
}
}
}
E finalmente o código para a classe principal:
package arvore_binaria;
import java.util.Scanner;
public class ArvoreBinariaTeste {
public static void main(String[] args) {
Scanner entrada = new Scanner(System.in);
// vamos criar um novo objeto da classe ArvoreBinariaBusca
ArvoreBinariaBusca arvore = new ArvoreBinariaBusca();
// vamos inserir 5 valores na árvore
for(int i = 0; i < 5; i++){
System.out.print("Informe um valor inteiro: ");
int valor = Integer.parseInt(entrada.nextLine());
// vamos inserir o nó e verificar o sucesso da operação
if(!arvore.inserir(valor)){
System.out.println("Não foi possível inserir." +
" Um elemento já contém este valor.");
}
}
// vamos pesquisar um valor na árvore
System.out.print("\nInforme o valor a ser pesquisado: ");
int valorPesquisa = Integer.parseInt(entrada.nextLine());
// obtém um objeto da classe NoArvore a partir do
// método pesquisar() da classe ArvoreBinariaBusca
No res = arvore.pesquisar(valorPesquisa);
// o valor foi encontrado?
if(res != null){
System.out.println("O valor foi encontrado na árvore");
}
else{
System.out.println("O valor não foi encontrado na árvore");
}
System.out.println("\n");
}
}
|
LISP ::: LISP para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como converter Coordenadas Polares para Coordenadas Cartesianas em LISP - LISP para EngenhariaQuantidade de visualizações: 757 vezes |
|
Nesta nossa série de LISP e AutoLISP para Geometria Analítica e Álgebra Linear, mostrarei um código 100% funcional para fazer a conversão entre coordenadas polares e coordenadas cartesianas. Esta operação é muito frequente em computação gráfica e é parte integrante das disciplinas dos cursos de Engenharia (com maior ênfase na Engenharia Civil). Na matemática, principalmente em Geometria e Trigonometria, o Sistema de Coordenadas Polares é um sistema de coordenadas em duas dimensões no qual cada ponto no plano é determinado por sua distância a partir de um ponto de referência conhecido como raio (r) e um ângulo a partir de uma direção de referência. Este ângulo é normalmente chamado de theta (__$\theta__$). Assim, um ponto em Coordenadas Polares é conhecido por sua posição (r, __$\theta__$). Já o sistema de Coordenadas no Plano Cartesiano, ou Espaço Cartesiano, é um sistema que define cada ponto em um plano associando-o, unicamente, a um conjuntos de pontos numéricos. Dessa forma, no plano cartesiano, um ponto é representado pelas coordenadas (x, y), com o x indicando o eixo horizontal (eixo das abscissas) e o y indicando o eixo vertical (eixo das ordenadas). Quando saímos do plano (espaço 2D ou R2) para o espaço (espaço 3D ou R3), temos a inclusão do eixo z (que indica profundidade). Antes de prosseguirmos, veja uma imagem demonstrando os dois sistemas de coordenadas: 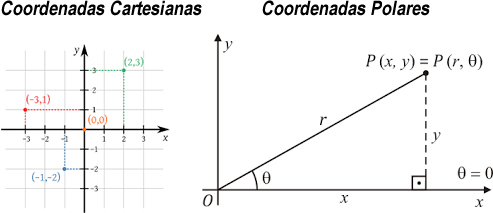 A fórmula para conversão de Coordenadas Polares para Coordenadas Cartesianas é: x = raio × coseno(__$\theta__$) y = raio × seno(__$\theta__$) E aqui está o código LISP completo que recebe as coordenadas polares (r, __$\theta__$) e retorna as coordenadas cartesianas (x, y):
; programa LISP que converte Coordenadas Polares
; em Coordenadas Cartesianas
(let((raio)(theta)(graus)(x)(y))
; vamos ler o raio e o ângulo
(princ "Informe o raio: ")
(force-output)
(setq raio (read))
(princ "Informe o theta: ")
(force-output)
(setq theta (read))
(princ "Theta em graus (1) ou radianos (2): ")
(force-output)
(setq graus (read))
; o theta está em graus?
(if(eq graus 1)
(setq theta (* theta (/ pi 180.0)))
)
; fazemos a conversão para coordenadas cartesianas
(setq x (* raio (cos theta)))
(setq y (* raio (sin theta)))
; exibimos o resultado
(format t "As Coordenadas Cartesianas são: (x = ~F, y = ~F)"
x y)
)
Ao executar este código LISP nós teremos o seguinte resultado: Informe o raio: 1 Informe o theta: 1.57 Theta em graus (1) ou radianos (2): 2 As Coordenadas Cartesianas são: (x = 0,00, y = 1,00) |
Ruby ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como ordenar um array em Ruby usando as funções sort e sort!Quantidade de visualizações: 12258 vezes |
|
Em várias situações nós precisamos ordenar arrays na linguagem Ruby. Para isso nós podemos usar a função sort, que ordenará os elementos do array em ordem crescente. Veja o código Ruby a seguir: =begin Este trecho de código mostra como ordenar um array de inteiros usando o método sort da classe Array. =end # define um array de inteiros valores = [10, 3, 56, 100, 34, 0, 4] # exibe os valores na ordem original puts "Ordem original:" for valor in valores print valor.to_s + " " end # array ordenado puts "\n\nOrdenado do menor para o maior:" valores = valores.sort # ordena o array for valor in valores print valor.to_s + " " end Ao executar este código Ruby nós teremos o seguinte resultado: Ordem original: 10 3 56 100 34 0 4 Ordenado do menor para o maior: 0 3 4 10 34 56 100 Se quisermos que a ordenação seja feita no array original, sem criar uma cópia, podemos usar a função sort!. Veja: =begin Este trecho de código mostra como ordenar um array de inteiros usando o método sort da classe Array. =end # define um array de inteiros valores = [10, 3, 56, 100, 34, 0, 4] # exibe os valores na ordem original puts "Ordem original:" for valor in valores print valor.to_s + " " end # array ordenado puts "\n\nOrdenado do menor para o maior:" valores.sort! # ordena o array for valor in valores print valor.to_s + " " end |
React Native ::: React Native - Componentes Visuais ::: Button |
Como detectar um clique em um botão do React Native e exibir uma mensagem AlertQuantidade de visualizações: 1381 vezes |
|
Nesta dica mostrarei como detectar um evento onPress em um botão do React Native e exibir uma mensagem usando o método alert() do componente Alert. Note que o evento onPress é disparado quando o usuário pressiona o botão. Veja o código completo para o exemplo:
import React, {Component} from 'react';
import {View, Button, Alert} from 'react-native';
type Props = {};
export default class App extends Component<Props> {
render() {
return (
<View style={{backgroundColor: '#eeeeee',
padding: 30}}>
<Button onPress = {() =>
Alert.alert("Bem-vindo(a) ao React Native")}
title="Clique" />
</View>
);
}
}
Veja que este exemplo define o código a ser chamado quando o botão for clicado diretamente em sua declaração. Em outras dicas dessa seção você verá como clicar no botão e chamar uma função JavaScript residente fora da declaração do botão. |
Java ::: Classes e Componentes ::: JButton |
Como definir a cor do texto de um botão JButton do Java SwingQuantidade de visualizações: 9567 vezes |
|
Nesta dica eu mostrarei como é possível definir a cor do texto de um componente JButton do Java Swing. Para isso nós usamos o método setForeground() da classe JButton, fornecendo a cor desejada, por exemplo, Color.RED. Veja um exemplo Java Swing completo:
package arquivodecodigos;
import java.awt.*;
import javax.swing.*;
public class Estudos extends JFrame{
public Estudos() {
super("Estudos Swing");
Container c = getContentPane();
c.setLayout(new FlowLayout(FlowLayout.LEFT));
// Cria um JButton com a cor do texto vermelho
JButton btn1 = new JButton("Clique Aqui!");
btn1.setForeground(Color.RED);
// Cria um JButton com a cor de fundo verde
JButton btn2 = new JButton("Clique Aqui!");
btn2.setForeground(Color.GREEN);
// Adiciona os botões à janela
c.add(btn1);
c.add(btn2);
setSize(350, 250);
setVisible(true);
}
public static void main(String args[]){
Estudos app = new Estudos();
app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
}
|
Python ::: Dicas & Truques ::: Strings e Caracteres |
Como transformar em letra maiúscula apenas o primeiro caractere de uma palavra ou frase usando a função capitalize() do PythonQuantidade de visualizações: 11716 vezes |
|
Nesta dica mostrarei como podemos usar o método capitalize() do objeto string da linguagem Python para transformar em letra maiúscula apenas a primeira letra de uma palavra, frase ou texto. Veja o trecho de código a seguir:
def main():
frase1 = "trabalho, Estudo e toco Guitarra."
# converte a primeira letra para maiúsculas e as demais
# para letras minúsculas
frase2 = frase1.capitalize()
# mostra os resultados
print("Frase original:", frase1)
print("Apenas a primeira letra maiúscula:", frase2)
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Frase original: trabalho, Estudo e toco Guitarra. Apenas a primeira letra maiúscula: Trabalho, estudo e toco guitarra. |
Python ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular o coeficiente angular de uma reta em Python dados dois pontos no plano cartesianoQuantidade de visualizações: 3236 vezes |
|
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x. Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:  Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é: \[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \] Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente. Veja agora o trecho de código na linguagem Python que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:
# vamos importar o módulo Math
import math as math
def main():
# x e y do primeiro ponto
x1 = float(input("Coordenada x do primeiro ponto: "))
y1 = float(input("Coordenada y do primeiro ponto: "))
# x e y do segundo ponto
x2 = float(input("Coordenada x do segundo ponto: "))
y2 = float(input("Coordenada y do segundo ponto: "))
# agora vamos calcular o coeficiente angular
m = (y2 - y1) / (x2 - x1)
# e mostramos o resultado
print("O coeficiente angular é: %f\n\n" % m)
if __name__== "__main__":
main()
Ao executar este código em linguagem Python nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 3 Coordenada y do primeiro ponto: 6 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 10 O coeficiente angular é: 0.666667 Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):
# vamos importar o módulo Math
import math as math
def main():
# x e y do primeiro ponto
x1 = float(input("Coordenada x do primeiro ponto: "))
y1 = float(input("Coordenada y do primeiro ponto: "))
# x e y do segundo ponto
x2 = float(input("Coordenada x do segundo ponto: "))
y2 = float(input("Coordenada y do segundo ponto: "))
# vamos obter o comprimento do cateto oposto
cateto_oposto = y2 - y1
# e agora o cateto adjascente
cateto_adjascente = x2 - x1
# vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
# (em radianos, não se esqueça)
tetha = math.atan2(cateto_oposto, cateto_adjascente)
# e finalmente usamos a tangente desse ângulo para calcular
# o coeficiente angular
tangente = math.tan(tetha)
# e mostramos o resultado
print("O coeficiente angular é: %f\n\n" % tangente)
if __name__== "__main__":
main()
Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta: 1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0; 2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0; 3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0). 4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe. |
Python ::: Dicas & Truques ::: Lista (List) |
Como excluir e retornar o primeiro item de uma lista Python usando a função pop()Quantidade de visualizações: 7516 vezes |
|
Em algumas situações nós precisamos remover e retornar um determinado elemento de uma list em Python. Para isso nós podemos usar o método pop(), já embutida na linguagem. A função pop(), quando usada sem argumentos, exclui e retorna o último elemento de uma lista. Se fornecido um argumento, a função remove e retorna o elemento no índice indicado. Se o índice informado estiver fora da faixa permitida, um erro do tipo IndexError será retornado. Veja um trecho de código Python no qual removemos e retornamos o primeiro elemento da lista:
def main():
# cria uma lista de inteiros
valores = [4, 23, 7, 1, 0, 54]
# imprime a lista
print(valores)
# remove o primeiro item
valor = valores.pop(0)
print("Item removido:", valor)
# exibe a lista novamente
print(valores)
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: [4, 23, 7, 1, 0, 54] Item removido: 4 [23, 7, 1, 0, 54] Experimente rodar esse código e fornecer, por exemplo, o valor 50 para o índice. Você verá o seguinte erro:
Exception has occurred: IndexError
pop index out of range
File "C:\estudos_python\estudos.py",
line 9, in main
valor = valores.pop(90)
File "C:\estudos_python\estudos.py", line
16, in <module>
main()
|
JavaScript ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Adicionando três elementos ao final de um vetor em JavaScript usando o método push() do objeto Array - Como adicionar elementos ao final de um vetor usando JavaScript - RevisadoQuantidade de visualizações: 7303 vezes |
Neste dica mostrarei como usar o método push() do objeto Array da linguagem JavaScript para adicionar três elementos ao final de um vetor. Veja o código completo, incluindo a página HTML que permite executar o exemplo:
<html>
<head>
<meta charset="utf-8">
<title>Estudos JavaScript</title>
</head>
<body>
<script type="text/javascript">
// vamos declarar e instanciar um vetor com 5 elementos
var valores = new Array(1, 2, 3, 4, 5);
document.write("Valores no vetor: " + valores + "<br>");
// agora vamos adicionar mais três elementos
valores.push(6, 7, 8);
document.write("Valores no vetor: " + valores);
</script>
</body>
</html>
Ao abrir esta página HTML nós teremos o seguinte resultado: Valores no vetor: 1,2,3,4,5 Valores no vetor: 1,2,3,4,5,6,7,8 |
Nossas 20 dicas & truques de programação mais populares |
|
Python - Como verificar se uma string contém apenas caracteres de espaços em Python usando a função isspace() Portugol - Como calcular o coeficiente angular de uma reta em Portugol dados dois pontos no plano cartesiano |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Java - Como inserir uma substring em uma string em Java usando o método insert() da classe StringBuffer Fórmulas da Física - Fórmula da Velocidade - Como calcular a velocidade quando temos a distância percorrida e o tempo gasto C - Como calcular a massa de um corpo dada sua energia cinética e sua velocidade usando a linguagem C |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





