Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica.

	E-Book 650 Dicas, Truques e Exercícios Resolvidos de Python - PDF com 1.200 páginas
	Domine lógica de programação e a linguagem Python com o nosso E-Book 650 Dicas, Truques e Exercícios Exercícios de Python, para você estudar onde e quando quiser. Este e-book contém dicas, truques e exercícios resolvidos abrangendo os tópicos: Python básico, matemática e estatística, banco de dados, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.
	Ver Conteúdo do E-book Apenas R$ 32,90

Java ::: Java para Engenharia ::: Geometria Analítica e Álgebra Linear

Como converter Coordenadas Cartesianas para Coordenadas Polares usando Java - Java para Engenharia

Quantidade de visualizações: 2215 vezes

Nesta nossa série de Java para Geometria Analítica e Álgebra Linear, mostrarei um código 100% funcional para fazer a conversão entre coordenadas cartesianas e coordenadas polares. Esta operação é muito frequente em computação gráfica e é parte integrante das disciplinas dos cursos de Engenharia (com maior ênfase na Engenharia Civil).

Na matemática, principalmente em Geometria e Trigonometria, o sistema de Coordenadas no Plano Cartesiano, ou Espaço Cartesiano, é um sistema que define cada ponto em um plano associando-o, unicamente, a um conjuntos de pontos numéricos.

Dessa forma, no plano cartesiano, um ponto é representado pelas coordenadas (x, y), com o x indicando o eixo horizontal (eixo das abscissas) e o y indicando o eixo vertical (eixo das ordenadas). Quando saímos do plano (espaço 2D ou R2) para o espaço (espaço 3D ou R3), temos a inclusão do eixo z (que indica profundidade).

Já o sistema de Coordenadas Polares é um sistema de coordenadas em duas dimensões no qual cada ponto no plano é determinado por sua distância a partir de um ponto de referência conhecido como raio (r) e um ângulo a partir de uma direção de referência. Este ângulo é normalmente chamado de theta (__$\theta__$). Assim, um ponto em Coordenadas Polares é conhecido por sua posição (r, __$\theta__$).

Antes de prosseguirmos, veja uma imagem demonstrando os dois sistemas de coordenadas: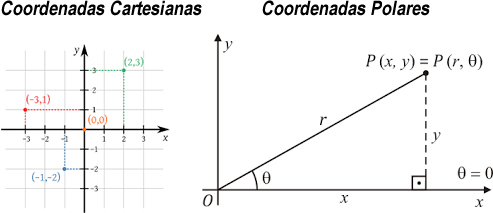

A fórmula para conversão de Coordenadas Cartesianas para Coordenadas Polares é:

__$r = \sqrt{x^2+y2}__$
__$\theta = \\arctan\left(\frac{y}{x}\right)__$

E aqui está o código Java completo que recebe as coordenadas cartesianas (x, y) e retorna as coordenadas polares (r, __$\theta__$):

package arquivodecodigos;
 
import java.util.Scanner;

public class Estudos{
  public static void main(String args[]){
    Scanner entrada = new Scanner(System.in);
    // vamos ler as coordenadas cartesianas
    System.out.print("Valor de x: ");
    double x = Double.parseDouble(entrada.nextLine());
    System.out.print("Valor de y: ");
    double y = Double.parseDouble(entrada.nextLine());
    
    // vamos calcular o raio
    double raio = Math.sqrt(Math.pow(x, 2) + Math.pow(y, 2));  

    // agora calculamos o theta (ângulo) em radianos 
    double theta = Math.atan2(y, x);

    // queremos o ângulo em graus também
    double angulo_graus = 180 * (theta / Math.PI); 

    // e exibimos o resultado
    System.out.println("As Coordenadas Polares são:\n" +
      "raio = " + raio + ", theta = " + theta + ", ângulo em graus = " +
      angulo_graus);
  }
}

Ao executar este código nós teremos o seguinte resultado:

Valor de x: -1
Valor de y: 1
As Coordenadas Polares são:
raio = 1.4142135623730951, theta = 2.356194490192345, ângulo em graus = 135.0

Veja que as coordenadas polares equivalentes são (__$\sqrt{2}__$, __$\frac{3\pi}{4}__$), com o theta em radianos. Sim, os professores das disciplinas de Geometria Analítica e Álgebra Linear, Física e outras gostam de escrever os resultados usando raizes e frações em vez de valores reais.

C# ::: Fundamentos da Linguagem ::: Estruturas de Controle

Como usar o laço do...while da linguagem C#

Quantidade de visualizações: 11899 vezes

O laço do...while (faça...enquanto) é usado quando queremos repetir uma instrução ou bloco de instruções ENQUANTO uma condição for satisfatória. A única diferença entre este laço e o laço while, é que, no laço do...while a condição de parada é testada após a iteração, o que garante que o laço do...while será executado no mínimo uma vez. No laço while a condição é testada antes da iteração. Veja um exemplo:

static void Main(string[] args){
  int valor = 1;

  do{
    Console.WriteLine("{0}", valor);
    valor++;
  }while(valor <= 10);

  Console.WriteLine("\n\nPressione uma tecla para sair...");
  Console.ReadKey();
}

Este trecho de código conta de 1 até 10. Veja que após cada iteração do laço nós testamos se o valor da variável de controle é menor ou igual a 10. A próxima iteração acontece somente se esta condição for satisfeita. Note ainda que dentro de cada iteração nós incrementamos o valor da variável de controle. Isso é feito para que o laço não seja executado infinitamente.

Veja um outro exemplo de laço do...while, desta vez simulando um menu de opções:

static void Main(string[] args){
  // variável que registra a opção do usuário
  int opcao;

  // laço do..while que mostra as opções do menu enquanto
  // o valor -1 não for informado
  do{
    // lê a opção
    Console.Write("Informe a opção 1, 2 ou 3" +
      " (-1 para sair): ");
    opcao = int.Parse(Console.ReadLine());

    switch (opcao){
      case 1:
        Console.WriteLine("Executando a opção 1");
        break;
      case 2:
        Console.WriteLine("Executando a opção 2");
        break;
      case 3:
        Console.WriteLine("Executando a opção 3");
        break;
      default:
        Console.WriteLine("Opção incorreta");
        break;
    }
  }while(opcao != -1);

  Console.WriteLine("\n\nPressione uma tecla para sair...");
  Console.ReadKey();
}

O laço do...while não é tão usado quanto o laço while. Use-o naquelas situações em que o laço deverá ser executado no mínimo uma vez.

JavaScript ::: Dicas & Truques ::: Cookies

Como verificar se cookies estão habilitados no navegador do usuário usando JavaScript

Quantidade de visualizações: 149 vezes

Em algumas situações nós gostaríamos de checar se os cookies estão habilitados no browser do usuário antes de gravarmos alguma informação. Nesta dica eu mostro como isso pode ser feito.

Note que tudo que precisamos fazer é criar um cookie temporário e tentar acessá-lo em seguida. Veja o código completo para o exemplo (incluindo a página HTML):

<!doctype html>
<html>
<head>
 <title>Estudos JavaScript</title>
</head>
<body>

<script type="text/javascript">
  // vamos criar um cookie temporário
  var cookieTemp = (new Date()).getTime() + '';
   
  // colocamos o cookie como parte do documento
  document.cookie = "cookieTemp=" + cookieTemp + "; path=/";
   
  // o cookie existe?
  if (document.cookie.indexOf(cookieTemp, 0) < 0){
    window.alert("Os cookies não estão habilitados no seu navegador");  
  }
  else{
    window.alert("Os cookies estão habilitados no seu navegador");
  } 
</script>

</body>
</html>

Ao executar este código teremos o seguinte resultado:

Os cookies estão habilitados no seu navegador.

Java ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes)

Como retornar o tamanho de um array em Java usando a propriedade length do objeto Array

Quantidade de visualizações: 11292 vezes

Nesta dica mostrarei como usar a propriedade length de um vetor (array de uma linha e várias colunas) para retornar a quantidade de elementos que ele possui. Este retorno é um número inteiro.

Veja o código completo:

package arquivodecodigos;

public class Estudos{
  public static void main(String[] args){
    // cria um vetor de cinco elementos
    String[] pessoas = {"Fábio", "Fernanda", 
      "Francisco", "João", "Osmar"};
       
    // obtém o tamanho do vetor
    int quant = pessoas.length;
    System.out.println("Este array possui " 
      + quant + " elementos");
       
    System.exit(0);
  }
}

Ao executarmos este código nós teremos o seguinte resultado:

Este array possui 5 elementos

Este código foi revisado e testado no Java 8.

wxWidgets ::: Dicas & Truques ::: wxApp

Como usar a classe wxApp em suas aplicações C++ wxWidgets

Quantidade de visualizações: 2109 vezes

A classe wxApp (Application Class) é uma das primeiras classes que devemos estudar se quisermos ter um domínio perfeito do framework wxWidgets. Para usá-la, devemos incluir #include <wx/app.h> em nossos códigos. Essa classe herda de wxAppConsole.

Todas as aplicações wxWidgets definem uma classe application derivada de wxApp. Há somente uma instância dela, e essa instância representa a aplicação sendo executada no momento.

De todos os métodos herdados de wxApp, há pelo menos um que devemos implementar, e ele é a função OnInit(), que é chamada quando o wxWidgets está pronto para executar o nosso código. OnInit() equivale ao main() em C/C++ ou WinMain (aplicações Win32).

Veja um trecho de código no qual declaramos e usamos a classe wxApp:

Código para aplicacao.h:

#include <wx/wx.h>

// arquivo de definição

// declaramos a classe application
class MinhaAplicacao : public wxApp{
public:
  // é chamado no startup da aplicação
  virtual bool OnInit();
};

// declara MinhaAplicacao& GetApp()
DECLARE_APP(MinhaAplicacao)

Código para aplicacao.cpp:

#include "aplicacao.h"

// arquivo de implementação

// aqui o wxWidgets implementa nosso objeto MinhaAplicacao
IMPLEMENT_APP(MinhaAplicacao)

bool MinhaAplicacao::OnInit(){
  // vamos mostrar uma mensagem ao iniciar a aplicação
  wxMessageDialog *alerta = new wxMessageDialog(NULL,
    wxT("A aplicação foi iniciada com sucesso"), wxT("Informação"), wxOK);
  alerta->ShowModal();

  // em geral retornamos true para iniciar o loop de eventos
  // mas essa aplicação exibe apenas uma janela de mensagem. Podemos sair
  return false;
}

Veja que no arquivo de declaração (header file) nós temos a macro DECLARE_APP. Ela nos permite declarar a função wxGetApp() que retorna uma referência para o objeto aplicação. Se não fizermos isso, a única forma de obter tal referência é usando o ponteiro global wxTheApp, que é do tipo wxApp*.

A macro IMPLEMENT_APP, no arquivo de implementação, permite ao wxWidgets criar dinamicamente uma instância do objeto application no ponto apropriado da inicialização da biblioteca.

Esse trecho de código é totalmente funcional, mas teremos apenas a exibição de uma mensagem wxMessageDialog. Por essa razão eu retornei false no laço de eventos. Se tivéssemos criado uma janela wxFrame, o retorno deveria ser true, já que teríamos de lidar com eventos.

Para finalizarmos, lembre-se de que o método OnInit() da classe wxApp é o local ideal para se fazer as verificações iniciais da aplicação, tais como conexão com banco de dados, permissão do usuário, disponibilidade da rede, etc.

Delphi ::: Dicas & Truques ::: Matemática e Estatística

Como calcular desvio padrão em Delphi - Delphi para Matemática e Estatística

Quantidade de visualizações: 2216 vezes

Em Matemática e Estatística, o Desvio padrão (em inglês: Standard Deviation) é uma medida de dispersão, ou seja, é uma medida que indica o quanto um conjunto de dados é uniforme. Quando o desvio padrão é baixo, isso quer dizer que os dados do conjunto estão mais próximos da média.

Como calcular o desvio padrão de um conjunto de dados? Vamos começar analisando a fórmula mais difundida na matemática e na estatística:

\[\sigma = \sqrt{ \frac{\sum_{i=1}^N (x_i -\mu)^2}{N}}\]

Onde:

a) __$\sigma__$ é o desvio;
b) __$x_i__$ é um valor qualquer no conjunto de dados na posição i;
c) __$\mu__$ é a média aritmética dos valores do conjunto de dados;
d) N é a quantidade de valores no conjunto.

O somatório dentro da raiz quadrada nos diz que devemos somar todos os elementos do conjunto, desde a posição 1 até a posição n, subtrair cada valor pela média do conjunto e elevar ao quadrado. Obtida a soma, nós a dividimos pelo tamanho do conjunto.

Veja o código Delphi completo que obtém o desvio padrão a partir de um conjunto de dados contendo quatro valores:

// Algoritmo Delphi para calcular desvio padrão

program estudos_delphi;

{$APPTYPE CONSOLE}

uses
  SysUtils, Math;

var
  // conjunto de dados
  conjunto: array[1..4] of double = (10, 30, 90, 30);
  soma: double; // Soma dos elementos
  desvio_padrao: double; // Desvio padrão
  tam: integer; // Tamanho dos dados
  media: double; // média
  i: integer;

begin
  soma := 0.0;
  desvio_padrao := 0.0;
  tam := 4;

  // vamos somar todos os elementos
  for i := 1 to tam do
    begin
      soma := soma + conjunto[i];
    end;

  // agora obtemos a média do conjunto de dados
  media := soma / tam;

  // e finalmente obtemos o desvio padrão
  for i := 1 to tam do
    begin
      // não esqueça de adicionar a unit Math
      desvio_padrao := desvio_padrao + Power(conjunto[i] - media, 2);
    end;

  // mostramos o resultado
  WriteLn('Desvio Padrão Populacional: ' + FloatToStr(Sqrt(desvio_padrao / tam)));
  WriteLn('Desvio Padrão Amostral: ' + FloatToStr(Sqrt(desvio_padrao / (tam - 1))));

  WriteLn;
  Write('Pressione Enter para sair...');
  ReadLn;

end.

Ao executar este código Delphi nós teremos o seguinte resultado:

Desvio Padrão Populacional: 30.0
Desvio Padrão Amostral: 34.64101615137755

Veja que, para calcular o Desvio Padrão Populacional, nós dividimos o somatório pela quantidade de elementos no conjunto, enquanto, para calcular o Desvio Padrão Amostral, nós dividimos o somatório pela quantidade de elementos - 1 (cuidado com a divisão por zero no caso de um conjunto com apenas um elemento).

Python ::: Dicas & Truques ::: Matemática e Estatística

Como calcular porcentagem em Python - Como efetuar cálculos de porcentagem em Python

Quantidade de visualizações: 26192 vezes

Cálculos de porcentagens estão presentes em boa parte das aplicações que desenvolvemos. Porém, há momentos em que a mente trava e não conseguimos lembrar com clareza como estes cálculos são feitos, principalmente em Python.

Esta anotação tem o objetivo de ser uma fonte de pesquisa para os momentos em que suas habilidades matemáticas insistirem em continuar ocultas.

Ex: 1 - Suponhamos que um produto que custe R$ 178,00 sofra um acréscimo de 15%. Qual o valor final do produto? Veja o código em Python:

# Algoritmo que calcula porcentagem em Python
def main():
  valor = 178.00 # valor original
  percentual = 15.0 / 100.0 # 15%
  valor_final = valor + (percentual * valor)

  # mostra o resultado
  print("O valor final do produto é: {0}".format(valor_final))

  # O resultado será 204,70
  
if __name__== "__main__":
  main()

Ex: 2 - Um produto, cujo valor original era de R$ 250,00, teve um desconto de 8%. Qual foi seu valor final? Veja o código em Python:

# Algoritmo que calcula porcentagem em Python
def main():
  valor = 250.00 # valor original
  percentual = 8.0 / 100.0 # 8%
  valor_final = valor - (percentual * valor)

  # mostra o resultado
  print("O valor final do produto é: {0}".format(valor_final))  
  # O resultado será 230,00
  
if __name__== "__main__":
  main()

Ex: 3 - Em um concurso de perguntas e respostas, um jovem acertou 72 das 90 perguntas apresentadas. Qual foi a porcentagem de acertos? E a porcentagem de erros? Veja o código em Python:

# Algoritmo que calcula porcentagem em Python
def main():
  perguntas = 90.0
  acertos = 72.0

  # mostra a porcentagem de acertos
  print("Porcentagem de acertos: {0}%".format((acertos / perguntas) * 100))

  # mostra a porcentagem de erros
  print("Porcentagem de erros: {0}%".format(((perguntas - acertos) / perguntas) * 100))

  # Os resultados serão 80% e 20%
  
if __name__== "__main__":
  main()

Ex: 4 - Um aparelho de CD foi adquirido por R$ 300,00 e revendido por R$ 340,00. Qual foi a porcentagem de lucro na transação? Veja o código em Python:

# Algoritmo que calcula porcentagem em Python
def main():
  valor_anterior = 300.0 # valor anterior
  novo_valor = 340.0 # valor novo

  # calcula a porcentagem de lucro
  # efetua o cálculo
  porcentagem_lucro = ((novo_valor * 100) / valor_anterior) - 100

  print("A porcentagem de lucro foi de: {0}%".format(porcentagem_lucro))

  # O resultado será 13,33
  
if __name__== "__main__":
  main()

Ex: 5 - Uma loja repassa 5% do lucro a seus vendedores. Se um produto custa R$ 70,00, qual o valor em reais repassado a um determinado vendedor? Veja o código em Python:

# Algoritmo que calcula porcentagem em Python
def main():
  valor = 70.0 # valor do produto
  percentual = 5.0 / 100.0 # 5%

  # calcula a comissão
  comissao = percentual * valor

  # mostra o resultado
  print("O valor repassado ao vendedor é: {0}".format(comissao))

  # O resultado será 3,5
  
if __name__== "__main__":
  main()

LISP ::: Desafios e Lista de Exercícios Resolvidos ::: Lisp Básico

Exercícios Resolvidos de Lisp - Como converter quilômetros em metros, centímetros e milímetros usando Lisp

Quantidade de visualizações: 1019 vezes

Pergunta/Tarefa:

Escreva um programa em Common Lisp para converter quilômetros em metros, centímetros e milímetros. Seu programa deverá pedir para o usuário informar a quantidade de quilômetros e exibir as conversões solicitadas.

Como sabemos, um Quilômetro = 1000 Metros, 100.000 Centímetros ou 1.000.000 Milímetros.

Seu programa deverá exibir uma saída parecida com:

Informe a distância em quilômetros: 2.5
Distância em Quilômetros: 2.5
Distância em Metros: 2500.0
Distância em Centímetros: 250000.0
Distância em Milímetros: 2500000.0

Resposta/Solução:

Veja a resolução comentada deste exercício usando Common Lisp:

; Variáveis usadas na resolução do problema
(let ((quilometros)(metros)(centimetros)(milimetros))
  ; vamos ler a quantidade de quilômetros
  (princ "Informe a distância em quilômetros: ")
  ; talvez o seu compilador não precise disso
  (force-output)
  ; atribui o valor lido à variável quilometros
  (setq quilometros (read))
  
  ; vamos calcular a distância em metros
  (setq metros (* quilometros 1000.0))
  ; vamos calcular a distância em centímetros
  (setq centimetros (* quilometros 100000.0))
  ; e agora a distância em milímetros
  (setq milimetros (* quilometros 1000000.0))
  
  ; E mostramos o resultado
  (format t "Distância em Quilômetros: ~F" quilometros)
  (format t "~%Distância em Metros: ~F" metros)
  (format t "~%Distância em Centímetros: ~F" centimetros)
  (format t "~%Distância em Milímetros: ~F" milimetros)
)

Python ::: Python para Engenharia ::: Unidades de Medida

Como converter Metros Quadrados em Quilômetros Quadrados em Python - Python para Física e Engenharia

Quantidade de visualizações: 428 vezes

Em muitas situações nós temos uma medida de área em m² e queremos transformá-la em km², ou seja, converter Metros Quadrados para Quilômetros Quadrados. Para isso só precisamos dividir os metros quadrados por 1.000.000.

Veja a fórmula:

\[\text{Quilômetros Quadrados} = \frac{\text{Metros Quadrados}}{1.000.000} \]

Agora veja o código Python que pede para o usuário informar a medida de área em metros quadrados e a converte para quilômetros quadrados. Note que mostrei como exibir o resultado em notação científica e sem notação científica:

# função principal do programa
def main():
  # vamos ler a medida em metros quadrados
  m_quadrados = float(input("Informe os metros quadrados: "))
  
  # agora calculamos os quilômetros quadrados
  km_quadrados = m_quadrados / 1000000.00
    
  # e mostramos o resultado
  print("Você informou {0} metros quadrados.".format(m_quadrados))
  print("Isso equivale a {0} quilômetros quadrados.".format(km_quadrados))
  print(f"Sem notação científica: {km_quadrados:.6f}")
  
if __name__== "__main__":
  main()

Ao executar este código Python nós teremos o seguinte resultado:

Informe os metros quadrados: 80
Você informou 80.0 metros quadrados.
Isso equivale a 8.0E-5 quilômetros quadrados.
Sem notação científica: 0,000080

HTML5 ::: HTML5 + JavaScript ::: Canvas

Como usar o método arc() do objeto Canvas do HTML5 para desenhar arcos, curvas e círculos

Quantidade de visualizações: 4321 vezes

O método arc() do objeto Canvas do HTML5 nos permite criar figuras tais como arcos, curvas e círculos. Para isso é importante entender os seus parâmetros:

arc(x, y, radius, ang1, ang2, direction);

Os parâmetros x e y indicam as coordenadas do centro do círculo. O parâmetro radius indica o raio do círculo. Os parâmetros ang1 e ang2 indicam o ângulo inicial e o ângulo final. O parâmetro direction indica a direção do desenho. Se o valor true for informado, a direção será anti-horário. Se for false, o desenho será no sentido horário.

É importante observar que os ângulos são medidos em radianos, não em graus. Assim, o ângulo 0 representa a posição 3 horas no relógio. A posição de 9 horas é (1 * PI), 12 horas é (1.5 * PI) e 6 horas é (0.5 * PI). Portanto, se você quiser desenhar um círculo completo, deverá sair do ângulo 0 e ir até (2 * PI).

Veja um trecho de código que desenha um arco equivalente a um quarto de uma pizza, ou seja, 25%, saindo do ângulo 90º (em graus) e indo até 180º (graus):

<html>
<head>
  <meta charset="utf-8">
  <title>Estudos HTML5</title>
</head>
<body>

<Canvas id="canvas1" width="500" height="350"></Canvas>
 
<script type="text/javascript">
  // obtemos uma referência ao elemento Canvas  
  var canvas = document.getElementById("canvas1");
  // obtemos o contexto de desenho
  var contexto = canvas.getContext("2d");
     
  // vamos desenhar um arco sem preenchimento com raio de 80
  contexto.beginPath(); // início um novo caminho
  // o arco começa no x = 100, y = 100, começa no ângulo 90 (em graus)
  // e vai até o ânculo 180 (graus)
  // as medidas na função arc() são em radianos, não em graus
  contexto.arc(100, 100, 80, Math.PI, 1.5 * Math.PI, false);
  contexto.lineWidth = 2; // largura da linha
  contexto.strokeStyle = '#990000'; // cor da linha
 
  contexto.stroke(); // realiza o desenho    
</script>

</body>
</html>

Execute este código e veja que o arco realmente foi desenhado. Seu resultado deverá ser parecido com: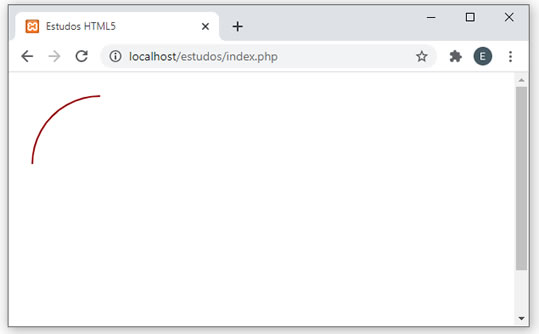

No entanto, para parecer um pedação de pizza, ou seja, o ponto de partida para um gráfico de pizza, é preciso que tenhamos duas linhas ligado esse arco ao centro do círculo. Veja a modificação que fiz:

<html>
<head>
  <meta charset="utf-8">
  <title>Estudos HTML5</title>
</head>
<body>

<Canvas id="canvas1" width="500" height="350"></Canvas>
 
<script type="text/javascript">
  // obtemos uma referência ao elemento Canvas  
  var canvas = document.getElementById("canvas1");
  // obtemos o contexto de desenho
  var contexto = canvas.getContext("2d");
     
  // vamos desenhar um arco sem preenchimento com raio de 80
  contexto.beginPath(); // início um novo caminho
   
  // primeiro movemos a caneta de desenho para o centro do círculo
  contexto.moveTo(100, 100);
 
  // o arco começa no x = 100, y = 100, começa no ângulo 90 (em graus)
  // e vai até o ânculo 180 (graus)
  // as medidas na função arc() são em radianos, não em graus
  contexto.arc(100, 100, 80, Math.PI, 1.5 * Math.PI, false);
  contexto.lineWidth = 2; // largura da linha
  contexto.strokeStyle = '#990000'; // cor da linha
 
  // agora desenhamos uma linha de volta para o arco
  contexto.lineTo(100, 100);
 
  contexto.stroke(); // realiza o desenho    
</script>

</body>
</html>

Execute novamente e veja que agora o efeito ficou bem melhor. Seu resultado deverá ser parecido com: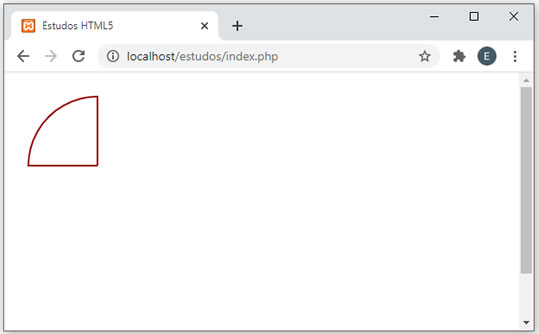

Para finalizar, vamos colorir o pedação de pizza. Veja a nova versão (com o código completo):

<!doctype html>
<html>
<head>
  <title>O objeto Canvas do HTML5</title>
</head>
 
<body>
 
<Canvas id="canvas1" width="500" height="350"></Canvas>
 
<script type="text/javascript">
  // obtemos uma referência ao elemento Canvas  
  var canvas = document.getElementById("canvas1");
  // obtemos o contexto de desenho
  var contexto = canvas.getContext("2d");
     
  // vamos desenhar um arco sem preenchimento com raio de 80
  contexto.beginPath(); // início um novo caminho
   
  // primeiro movemos a caneta de desenho para o centro do círculo
  contexto.moveTo(100, 100);
 
  // o arco começa no x = 100, y = 100, começa no ângulo 90 (em graus)
  // e vai até o ânculo 180 (graus)
  // as medidas na função arc() são em radianos, não em graus
  contexto.arc(100, 100, 80, Math.PI, 1.5 * Math.PI, false);
  contexto.lineWidth = 2; // largura da linha
  contexto.strokeStyle = '#990000'; // cor da linha
 
  // agora desenhamos uma linha de volta para o arco
  contexto.lineTo(100, 100);
 
  // vamos preencher o gráfico
  contexto.fillStyle = "#CCCCCC"; // cor do preenchimento
  contexto.fill(); // preenche de fato
 
  contexto.stroke(); // realiza o desenho    
</script>
 
</body>
</html>

Agora o resultado será: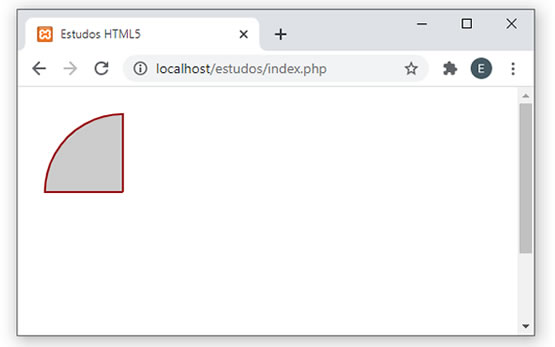

Carregar Publicações Anteriores

Nossas 20 dicas & truques de programação mais populares

Java - Como usar o método System.out.printf() do Java para converter um valor na base decimal para hexadecimal

Java - Como calcular raiz quadrada em Java usando a função sqrt() da classe Math

Rust - Exercício Resolvido de Rust - Como testar se um ano é bissexto em Rust - Um programa que lê um ano com quatro dígitos e informa se ele é bissexto ou não

PHP - Como resolver uma equação do segundo grau em PHP - Como calcular Bhaskara em PHP

PHP - PHP para iniciantes - Como usar o tipo de dados float do PHP

Java - Java Swing - Como salvar o conteúdo de um JTextArea em um arquivo (usando um JFileChooser para localizar o diretório e arquivo)

Java - Como arredondar um número para cima em Java usando a função ceil() da classe Math

Python - Exercícios Resolvidos de Python - Como calcular o peso de uma pessoa na Lua usando Python

Java - Exercícios Resolvidos de Java - Ler um número de três dígitos, separá-lo e invertê-lo, escrevendo o número lido e sua forma inversa

Ruby - Como converter uma string em um valor de ponto-flutuante em Ruby usando a função to_f da classe String

VB.NET - Como calcular vetor unitário em VB.NET - VB.NET para Física e Engenharia

Java - Como testar o conteúdo no final de uma string usando Java - O método endsWith() da classe String

JavaScript - Como formatar datas em JavaScript de acordo com as configurações do computador do usuário usando a função toLocaleDateString()

C - Como calcular a transposta de uma matriz em C - Curso de C para Geometria Analítica e Álgebra Linear

Java - Como converter Centímetros Cúbicos em Metros Cúbicos em Java - Java para Física e Engenharia

Java - Como calcular a área de um círculo em Java dado o raio do círculo

Java - Exercício Resolvido de Java - Faça um programa que sorteie um número aleatório entre 0 e 500 e pergunte ao usuário qual é o "número mágico". O programa deverá

Portugol - Como testar se uma sub-cadeia está contida em uma cadeia de caracteres em Portugol usando a função posicao_texto()

Delphi - Como usar arrays (vetores e matrizes) em Delphi

Java - Como retornar uma lista de todos os IDs de fusos horários suportados pela linguagem Java usando o método getAvailableIDs() da classe TimeZone

Você também poderá gostar das dicas e truques de programação abaixo

Java - Tutorial Java para iniciantes - Como usar o laço for em Java

C++ - Exercícios Resolvidos de C++ - Como retornar o primeiro elemento de um vetor em C++

C# - C# para iniciantes - Como usar o tipo decimal da linguagem C#

C# - Como usar o laço do...while da linguagem C#

C# - Como usar os tipos de dados byte e sbyte da linguagem C#

Python - Exercício Resolvido de Python - Como calcular o Número de Reynolds em Python - Leite integral a 293 K, massa específica de 1030 kg/m3 e viscosidade de 2,12.10-3 N.s/m2 está escoando a uma razão

Python - Como construir uma data em Python usando o construtor da classe datetime

Delphi - Como excluir chaves no registro do Windows usando Delphi a função DeleteKey() da classe TRegistry do Delphi

Java - Como verificar se um arquivo ou diretório existe em Java usando o método exists() da classe File

JavaScript - Como remover elementos duplicados de um array em JavaScript usando um Set e o método Array.from()

Java - Como construir uma data no passado ou futuro em Java usando a classe GregorianCalendar

PHP - Como obter a quantidade de elementos em um vetor (array ou matriz de uma dimensão) em PHP

Python - Python para iniciantes - Como usar a instrução continue da linguagem Python

jQuery - Como remover atributos dos elementos HTML usando a função removeAttr() do jQuery

Python - Exercícios Resolvidos de Python - Qual seria a vazão (m3/h) de saída para uma bacia hidrográfica "completamente impermeável", com área de 60 km2, sob uma chuva constante

Java - Java Swing - Como detectar alterações no conteúdo de um JTextArea

Java - Estruturas de dados em Java - Como criar uma lista singularmente ligada, inserindo e exibindo os valores contidos em cada nó

Python - Datas e horas em Python - Como obter o nome do dia da semana no formato longo (segunda-feira, terça-feira, etc) usando a função strftime() do Python

Java - Exercícios Resolvidos de Java - Um programa que calcule e mostre a tabuada de multiplicação de um número digitado pelo usuário (entre 1 e 10)

PHP - Como verificar se uma variável PHP é do tipo object usando a função is_object()

Nossas 20 dicas & truques de programação mais recentes

Python - Código completo para um visualizador de fotos e imagens em PyQt - Carregar imagens com botões de próxima imagem e imagem anterior

Python - Como calcular a previsão de cargas de iluminação em instalações elétricas residenciais usando Python - Python para Instalações Elétricas Prediais

C++ - Exercício Resolvido de C++ - Escreva um programa C++ para alocar dinamicamente um inteiro, um caractere e uma string

Excel VBA - Como usar o evento Worksheet_Change do Excel VBA para detectar a linha e a coluna da célula que foi modificada

Python - Como criar um programa de desenho de linhas no estilo AutoCAD usando PyQt

Python - Como desenhar um ponto na janela principal de uma aplicação PyQt usando a função drawPoint() da classe QPainter

Java - Exercícios Resolvidos de Java - Uma pousada estipulou o preço para a sua diária em R$ 30,00 e mais uma taxa de serviços diários de

Portugol - Exercícios Resolvidos de Portugol - Uma pousada estipulou o preço para a sua diária em R$ 30,00 e mais uma taxa de serviços diários de

Python - Cálculo de estribos em vigas de concreto armado usando Python - Armadura mínima transversal normativa

VBA - Como adicionar dias à data atual em VBA usando a função DateAdd() - Datas e horas em VBA

VBA - Como exibir a data e hora atual em VBA usando a função Now() - Datas e horas em VBA

VBA - Como exibir a data atual em VBA usando a função Date - Datas e horas em VBA

VBA - Como usar o laço de repetição For Next em nossas aplicações VBA

VBA - Como extrair uma substring à direita de uma string em VBA usando a função Right()

VBA - Como extrair uma substring à esquerda de uma string em VBA usando a função Left()

Python - Cálculo de estribos em vigas de concreto armado usando Python - Verificação da compressão diagonal do concreto

Excel - Como gerar números aleatórios inteiros entre 1 e 10 no Excel usando as funções ALEATÓRIO() e INT()

Excel - Como gerar números aleatórios no Excel usando a função ALEATÓRIO() - Excel para Matemática e Estatística

Python - Como gerar valores igualmente espaçados em Python sem o uso de bibliotecas externas

Java - Como gerar valores igualmente espaçados em Java sem o uso de bibliotecas externas

Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site

Python - Como criar uma Agenda de Contatos em Python + MySQL - Projeto completo com código fonte - Versão console

Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado

Java - Como criar o jogo Pedra, Papel, Tesoura em Java - Jogo completo em Java com código comentado

Java - Como criar um Jogo da Velha em Java - Jogo completo com código fonte comentado - Versão console

PHP - Software de Gestão Financeira com código fonte em PHP, MySQL, Bootstrap, jQuery - Inclui cadastro de clientes, fornecedores e ticket de atendimento

PHP - Calendário de Eventos em PHP e MySQL - Código fonte completo com opções de cadastrar, listar, excluir, editar e listar eventos

PHP - Como criar um Cadastro de Usuários em PHP e MySQL - Cadastrar, Listar, Editar, Exluir e Pesquisar - Código fonte completo

Java - Sistema para Biblioteca usando Programação Orientada a Objetos em Java - Projeto completo com código fonte - Versão console

Java - Simulação de Sistema Bancário usando Programação Orientada a Objetos em Java - Projeto completo com código fonte - Versão console

PHP - Controle de Estoque completo com código fonte em PHP, MySQL, Bootstrap, jQuery - 100% funcional e fácil de modificar e implementar novas funcionalidades

Últimos Exercícios Resolvidos

C++ - Exercício Resolvido de C++ - Escreva um programa C++ para alocar dinamicamente um inteiro, um caractere e uma string

Java - Exercícios Resolvidos de Java - Uma pousada estipulou o preço para a sua diária em R$ 30,00 e mais uma taxa de serviços diários de

Portugol - Exercícios Resolvidos de Portugol - Uma pousada estipulou o preço para a sua diária em R$ 30,00 e mais uma taxa de serviços diários de

Portugol - Exercícios Resolvidos de Portugol - Sabe-se que a Camiseteria Kanashiro está com uma promoção de camisetas nos seguintes tamanhos e valores

Python - Exercício Resolvido de Python - Calcular o número de Reynolds e identificar se o escoamento é liminar ou turbulento sabendo-se que em uma tubulação com diâmetro de 40 mm

Java - Exercícios Resolvidos de Java - Escreva um programa Java que cria um objeto da classe Calendar para a data e hora atual e mostre os valores máximos para o ano, mês, dia e semana

Java - Exercícios Resolvidos de Java - Escreva um programa Java que construa um objeto da classe Calendar representando a data e hora atual e mostre os valores individuais de ano, mês, dia

Java - Exercícios Resolvidos de Java - Escreva um programa Java que pede para o usuário informar o dia, mês e ano e construa uma data usando um objeto da classe Calendar

C - Exercícios Resolvidos de C - Escreva um programa C que peça para o usuário informar um ano e informe o dia da semana que o ano começou (domingo, segunda-feira

C - Exercícios Resolvidos de C - Escreva um programa C que informa o número de dias em um determinado mês e ano. Seu código deverá solicitar ao usuário o número correspondente

Java - Exercícios Resolvidos de Java - Escreva um programa Java que pede para o usuário informar sua data de nascimento e mostre a idade em anos, meses e dias

Java - Exercícios Resolvidos de Java - Escreva um programa Java que mostre a data atual e a data que será daqui a 10 dias, ou seja, a data atual acrescida de 10 dias

Portugol - Exercícios Resolvidos de Portugol - Escreva um programa Portugol para mover todos os zeros para o final do vetor, sem alterar a ordem dos elementos já presentes no array

VisuAlg - Exercícios Resolvidos de VisuAlg - Um programa que lê duas notas, calcula a média aritmética e exibe uma mensagem de reprovado, exame ou aprovado

Portugol - Exercícios Resolvidos de Portugol - Um programa que lê duas notas, calcula a média aritmética e exibe uma mensagem de reprovado, exame ou aprovado

Python - Exercícios Resolvidos de Python - Faça um programa que leia a idade e o sexo de 5 pessoas, mostrando no final: a) Quantos homens foram cadastrados

Python - Exercícios Resolvidos de Python - Escreva um programa Python que pergunte a velocidade de um carro. Caso ultrapasse 80km/h, exiba uma mensagem dizendo que

C++ - Exercícios Resolvidos de C++ - Escreva um programa C++ que pergunte a velocidade de um carro. Caso ultrapasse 80km/h, exiba uma mensagem dizendo que

C - Exercícios Resolvidos de C - Escreva um programa C que pergunte a velocidade de um carro. Caso ultrapasse 80km/h, exiba uma mensagem dizendo que

VisuAlg - Exercícios Resolvidos de VisuAlg - Escreva um programa VisuAlg que pergunte a velocidade de um carro. Caso ultrapasse 80km/h, exiba uma mensagem dizendo que

E-Books em PDF

E-Book 350 Exercícios Resolvidos de Java - PDF com 500 páginas

Domine lógica de programação e a linguagem Java com o nosso E-Book 350 Exercícios Exercícios de Java, para você estudar onde e quando quiser.

Este e-book contém exercícios resolvidos abrangendo os tópicos: Java básico, matemática e estatística, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.

Ver Conteúdo do E-book

E-Book 650 Dicas, Truques e Exercícios Resolvidos de Python - PDF com 1.200 páginas

Domine lógica de programação e a linguagem Python com o nosso E-Book 650 Dicas, Truques e Exercícios Exercícios de Python, para você estudar onde e quando quiser.

Este e-book contém dicas, truques e exercícios resolvidos abrangendo os tópicos: Python básico, matemática e estatística, banco de dados, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.

Ver Conteúdo do E-book

Linguagens Mais Populares

1º lugar: Java
2º lugar: Python
3º lugar: C#
4º lugar: PHP
5º lugar: C
6º lugar: Delphi
7º lugar: JavaScript
8º lugar: C++
9º lugar: VB.NET
10º lugar: Ruby

Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica.

Java ::: Java para Engenharia ::: Geometria Analítica e Álgebra Linear

Como converter Coordenadas Cartesianas para Coordenadas Polares usando Java - Java para Engenharia

C# ::: Fundamentos da Linguagem ::: Estruturas de Controle

Como usar o laço do...while da linguagem C#

JavaScript ::: Dicas & Truques ::: Cookies

Como verificar se cookies estão habilitados no navegador do usuário usando JavaScript

Java ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes)

Como retornar o tamanho de um array em Java usando a propriedade length do objeto Array

wxWidgets ::: Dicas & Truques ::: wxApp

Como usar a classe wxApp em suas aplicações C++ wxWidgets

Delphi ::: Dicas & Truques ::: Matemática e Estatística

Como calcular desvio padrão em Delphi - Delphi para Matemática e Estatística

Python ::: Dicas & Truques ::: Matemática e Estatística

Como calcular porcentagem em Python - Como efetuar cálculos de porcentagem em Python

LISP ::: Desafios e Lista de Exercícios Resolvidos ::: Lisp Básico

Exercícios Resolvidos de Lisp - Como converter quilômetros em metros, centímetros e milímetros usando Lisp

Python ::: Python para Engenharia ::: Unidades de Medida

Como converter Metros Quadrados em Quilômetros Quadrados em Python - Python para Física e Engenharia

HTML5 ::: HTML5 + JavaScript ::: Canvas

Como usar o método arc() do objeto Canvas do HTML5 para desenhar arcos, curvas e círculos

Questões de Concurso para Engenharia Civil

Exercícios Resolvidos

Bancos de Dados

Questões de Concurso

Frameworks

Projetos e Códigos Fonte

Especializações

Calculadoras

Ferramentas

Todas as Linguagens, Frameworks, Biliotecas e Bancos de Dados

Compre pelo WhatsApp: +55 (062) 98553-6711

E-Book 350 Exercícios Resolvidos de Java - Com comentários em Português

PDF COM 500 PÁGINAS

Apenas R$ 19,90