Java ::: Dicas & Truques ::: Matemática e Estatística |
Como resolver uma equação do segundo grau em Java - Como calcular Bhaskara em JavaQuantidade de visualizações: 3049 vezes |
|
Nesta dica mostrarei como encontrar as raízes de uma equação quadrática, ou seja, uma equação do 2º usando a linguagem Java. Definimos como equação do 2º grau ou equações quadráticas qualquer equação do tipo ax² + bx + c = 0 em que a, b e c são números reais e a ≠ 0. Ela recebe esse nome porque, no primeiro membro da igualdade, há um polinômio de grau dois com uma única incógnita. Note que, dos coeficientes a, b e c, somente o a é diferente de zero, pois, caso ele fosse igual a zero, o termo ax² seria igual a zero, logo a equação se tornaria uma equação do primeiro grau: bx + c = 0. Independentemente da ordem da equação, o coeficiente a sempre acompanha o termo x², o coeficiente b sempre acompanha o termo x, e o coeficiente c é sempre o termo independente. Como resolver uma equação do 2º grau Conhecemos como soluções ou raízes da equação ax² + bx + c = 0 os valores de x que fazem com que essa equação seja verdadeira. Uma equação do 2º grau pode ter no máximo dois números reais que sejam raízes dela. Para resolver equações do 2º grau completas, existem dois métodos mais comuns: a) Fórmula de Bhaskara; b) Soma e produto. O primeiro método é bastante mecânico, o que faz com que muitos o prefiram. Já para utilizar o segundo, é necessário o conhecimento de múltiplos e divisores. Além disso, quando as soluções da equação são números quebrados, soma e produto não é uma alternativa boa. Como resolver uma equação do 2º grau usando Bhaskara Como nosso código Java vai resolver a equação quadrática usando a Fórmula de Bhaskara, o primeiro passo é encontrar o determinante. Veja: \[\Delta =b^2-4ac\] Nem sempre a equação possui solução real. O valor do determinante é que nos indica isso, existindo três possibilidades: a) Se determinante > 0, então a equação possui duas soluções reais. b) Se determinante = 0, então a equação possui uma única solução real. c) Se determinante < 0, então a equação não possui solução real. Encontrado o determinante, só precisamos substituir os valores, incluindo o determinante, na Fórmula de Bhaskara: \[x = \dfrac{- b\pm\sqrt{b^2- 4ac}}{2a}\] Vamos agora ao código Java. Nossa aplicação vai pedir para o usuário informar os valores dos três coeficientes a, b e c e, em seguida, vai apresentar as raizes da equação:
package estudos;
import java.util.Scanner;
public class Estudos{
public static void main(String[] args){
// para efetuar a leitura do usuário
Scanner entrada = new Scanner(System.in);
// os coeficientes
double a, b, c;
// as duas raizes, a imaginaria e o discriminante
double raiz1, raiz2, imaginaria, discriminante;
// vamos pedir para o usuário informar os valores dos coeficientes
System.out.print("Valor do coeficiente a: ");
a = Double.parseDouble(entrada.nextLine());
System.out.print("Valor do coeficiente b: ");
b = Double.parseDouble(entrada.nextLine());
System.out.print("Valor do coeficiente c: ");
c = Double.parseDouble(entrada.nextLine());
// vamos calcular o discriminante
discriminante = (b * b) - (4 * a * c);
// a equação possui duas soluções reais?
if(discriminante > 0){
raiz1 = (-b + Math.sqrt(discriminante)) / (2 * a);
raiz2 = (-b - Math.sqrt(discriminante)) / (2 * a);
System.out.println("Existem duas raizes: x1 = " + raiz1
+ " e x2 = " + raiz2);
}
// a equação possui uma única solução real?
else if(discriminante == 0){
raiz1 = raiz2 = -b / (2 * a);
System.out.println("Existem duas raizes iguais: x1 = "
+ raiz1 + " e x2 = " + raiz2);
}
// a equação não possui solução real?
else if(discriminante < 0){
raiz1 = raiz2 = -b / (2 * a);
imaginaria = Math.sqrt(-discriminante) / (2 * a);
System.out.println("Existem duas raízes complexas: x1 = " +
raiz1 + " + " + imaginaria + " e x2 = " + raiz2
+ " - " + imaginaria);
}
}
}
Ao executar este código Java nós teremos o seguinte resultado: Valor do coeficiente a: 1 Valor do coeficiente b: 2 Valor do coeficiente c: -3 Existem duas raizes: x1 = 1.0 e x2 = -3.0 |
JavaScript ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cosseno de um ângulo em JavaScript usando a função cos() do objeto Math - Calculadora de cosseno em JavaScriptQuantidade de visualizações: 7580 vezes |
|
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula: \[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \] Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da linguagem JavaScript. Esta função, que é parte do objeto Math, recebe um valor numérico e retorna um valor também numérico) entre -1 até 1 (ambos inclusos). Veja:
<html>
<head>
<title>Estudos JavaScript</title>
</head>
<body>
<script type="text/javascript">
// vamos calcular o cosseno de 3 números
document.writeln("Cosseno de 0 = " + Math.cos(0));
document.writeln("<br>Cosseno de 1 = " + Math.cos(1));
document.writeln("<br>Cosseno de 2 = " + Math.cos(2));
</script>
</body>
</html>
Ao executar este código JavaScript nós teremos o seguinte resultado: Cosseno de 0 = 1 Cosseno de 1 = 0.5403023058681398 Cosseno de 2 = -0.4161468365471424 Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: 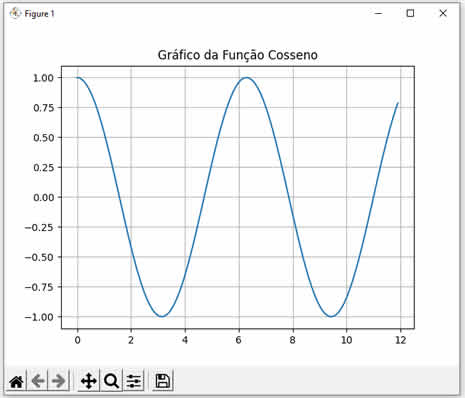 |
PHP ::: Fundamentos da Linguagem ::: Variáveis e Constantes |
Apostila PHP para iniciantes - Como usar constantes na linguagem PHPQuantidade de visualizações: 12090 vezes |
|
Como acontece na maioria das linguagens de programação, o PHP também permite o uso de constantes. Como o próprio nome diz, constantes são inicializadas uma vez e não podem ter seus valores alterados durante a execução do programa. A definição de constantes em PHP segue as mesmas regras de nomeação de variáveis, com a exceção de que constantes não possuem o símbolo $ e são geralmente escritas em letras maiúsculas. Diferente de variáveis, constantes, uma vez definidas, são acessadas globalmente. Não há a necessidade de redeclará-las em cada nova função ou arquivo. A síntaxe de definição de uma constante é: define("CONSTANT_NAME", value [, case_sensitivity]) onde: a) CONSTANT_NAME é o nome da constante; b) value é o valor atribuído à constante. Não é possível atribuir arrays nem objetos à constantes; c) case_sensitivity permite definir se o nome da constante será tratado igualmente se referenciado usando letras maiúsculas ou minúsculas. O valor padrão é true, o que quer dizer que "VALOR" e "Valor" serão tratados como uma única constante. REVISÃO: Revisando este código no PHP 8 eu percebi que o terceiro argumento (case_sensitivity) não é mais suportado, e gera um aviso do tipo: Warning: define(): Argument #3 ($case_insensitive) is ignored since declaration of case-insensitive constants is no longer supported in... Veja um exemplo de declaração e uso de constantes em PHP:
<?
// declara uma constante com o nome MODO e valor 2
define("MODO", 2);
echo "O valor definido é: " . MODO;
?>
Veja agora o que acontece quando tentamos modificar o valor de uma variável do tipo constante:
<?
// declara uma constante com o nome MODO e valor 2
define("MODO", 2);
// vamos tentar alterar o valor da constante
MODO = 10;
?>
Este código gera a seguinte mensagem de erro: Parse error: syntax error, unexpected token "=" in... |
Ruby ::: Dicas & Truques ::: Strings e Caracteres |
Como inserir uma substring em uma determinada posição de uma string em Ruby usando a função insert()Quantidade de visualizações: 8992 vezes |
|
Muita vezes precisamos inserir uma substring em uma determinada posição de uma string em Ruby. Esta tarefa pode ser realizada com a função insert() da classe String. Esta função opera na string original e requer dois argumentos: a posição na string onde a substring será inserida e a substring propriamente dita. A posição é um índice iniciando em 0. Índices negativos são contados a partir do final da string. Veja o exemplo: # declara e inicializa uma variável string frase = "Gosto muito de Ruby" puts "A frase original é: " + frase # vamos inserir " Python e" antes de "Ruby". frase.insert(14, " Python e") # exibe o resultado puts "A nova frase é: " + frase Ao executar este código Ruby nós teremos o seguinte resultado: A frase original é: Gosto muito de Ruby A nova frase é: Gosto muito de Python e Ruby |
C# ::: Dicas & Truques ::: Arquivos e Diretórios |
Como retornar o nome de um arquivo sem a extensão em C# usando o método GetFileNameWithoutExtension() da classe PathQuantidade de visualizações: 12907 vezes |
|
A função GetFileNameWithoutExtension() da classe Path do C# facilita o nosso trabalho quando precisamos obter o caminho e nome de um arquivo sem a sua extensão, ou seja, se o nome do arquivo for "video.mp4", a função nos retornará apenas "video". O método GetFileNameWithoutExtension() recebe uma string representando o caminho e nome do arquivo e retorna uma outra string contendo o nome do arquivo sem a extensão. Veja um exemplo completo de seu uso:
using System;
using System.Collections;
using System.IO;
namespace Estudos {
class Program {
static void Main(string[] args) {
// caminho e nome do arquivo com a extensão
string arquivo = "C:\\estudos_csharp\\texto.txt";
// obtém o nome do arquivo sem a extensão
string arquivo2 = Path.GetFileNameWithoutExtension(arquivo);
// exibe o resultado
Console.WriteLine("O nome do arquivo sem a extensão " +
"é: {0}", arquivo2);
Console.WriteLine("\n\nPressione qualquer tecla para sair...");
// pausa o programa
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: O nome do arquivo sem a extensão é: texto |
Ruby ::: Dicas & Truques ::: Programação Orientada a Objetos |
Como usar métodos e variáveis de classes em Ruby - Programação Orientada a Objetos em RubyQuantidade de visualizações: 8133 vezes |
|
Variáveis e métodos de classe, ao contrário de variáveis e métodos de instâncias, pertencem às classes e não às suas instâncias. Desta forma, uma variável ou método de classe é compartilhado por todos os objetos criados a partir de tal classe. Para que você entenda melhor, o exemplo abaixo mostra uma classe que contém uma variável e um método de classe. Execute o código e veja como o valor de @@quant_clientes é incrementado todas as vezes que um novo objeto da classe Cliente é criado:
# vamos criar a classe Cliente
class Cliente
# variável de classe
@@quant_clientes = 0;
def initialize
@@quant_clientes = @@quant_clientes + 1
end
# método de classe
def Cliente.obter_quant_clientes
@@quant_clientes
end
end
# vamos criar três objetos da classe Cliente
cliente1 = Cliente.new
cliente2 = Cliente.new
cliente3 = Cliente.new
# vamos obter a quantidade de clientes criados
quant = Cliente.obter_quant_clientes
# exibe o resultado
puts "Há " + quant.to_s + " clientes criados"
Ao executar este código Ruby nós teremos o seguinte resultado: Há 3 clientes criados |
Java ::: Classes e Componentes ::: JTextArea |
Java Swing - Como evitar a barra de rolagem horizontal em um JScrollPaneQuantidade de visualizações: 118 vezes |
|
Em algumas situações nós precisamos usar um JScrollPane para permitir as barras de rolagem em algum componente visual do Java Swing. Nesta dica eu mostro como isso pode ser feito, e mostro também como a barra de rolagem horizontal pode ser evitada. Este comportamento é o esperado quando estamos trabalhando com caixas de texto do tipo JTextArea. Veja um trecho de código no qual usamos a constante HORIZONTAL_SCROLLBAR_NEVER de ScrollPaneConstants para indicar que a barra horizontal não deverá ser exibida:
textArea = new JTextArea(10, 20);
JScrollPane scrollPane = new JScrollPane(textArea);
// Evitar o aparecimento da barra de rolagem horizontal
scrollPane.setHorizontalScrollBarPolicy(
ScrollPaneConstants.HORIZONTAL_SCROLLBAR_NEVER);
|
Elixir ::: Dicas de Estudo e Anotações ::: Passos Iniciais |
Como instalar a linguagem de programação Elixir no WindowsQuantidade de visualizações: 802 vezes |
|
Está curioso(a) para aprender um pouco mais sobre a linguagem de programação Elixir? Nesta dica mostrarei como instalar, configurar e testar o ambiente de programação desta linguagem. O primeiro passo para instalar a Elixir no Windows é verificar se você já tem uma instalação do ambiente de programação Erlang. Se ainda não tiver, veja a nossa dica correspondente. Como baixar e instalar a Elixir Para baixar a Elixir e as ferramentas necessárias, acesse a URL https://elixir-lang.org/install.html#windows e baixe o instalador elixir-websetup.exe. Em seguida dê duplo-clique neste instalador e siga as instruções apresentadas. Não se preocupe. Basta aceitar as opções padrões que o instalador fará a instalação completa, inclusive incluindo o diretório bin na variável de ambiente PATH. Como testar a instalação da Elixir Para testar se sua instalação da linguagem de programação Elixir ocorreu sem problemas, abra uma nova janela de terminal e dispare o seguinte comando: C:\Users\Osmar>elixirc --version Se tudo correu bem você verá o seguinte resultado: Erlang/OTP 25 [erts-13.2] [source] [64-bit] [smp:4:4] [ds:4:4:10] [async-threads:1] [jit:ns] Elixir 1.14.3 (compiled with Erlang/OTP 25) Pronto! Agora é só seguir as nossas dicas e truques de Elixir e ficar fluente em mais essa linguagem de programação. Bons estudos! |
PHP ::: PHP para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como somar os elementos da diagonal principal de uma matriz em PHPQuantidade de visualizações: 2604 vezes |
|
A Matriz quadrada é um tipo especial de matriz que possui o mesmo número de linhas e o mesmo número de colunas, ou seja, dada uma matriz Anxm, ela será uma matriz quadrada se, e somente se, n = m, onde n é o número de linhas e m é o número de colunas. Em geral as matrizes quadradas são chamadas de Matrizes de Ordem n, onde n é o número de linhas e colunas. Dessa forma, uma matriz de ordem 4 é uma matriz que possui 4 linhas e quatro colunas. Toda matriz quadrada possui duas diagonais, e elas são muito exploradas tanto na matemática quanto na construção de algorítmos. Essas duas diagonais são chamadas de Diagonal Principal e Diagonal Secundária. A diagonal principal de uma matriz quadrada une o seu canto superior esquerdo ao canto inferior direito. Veja: 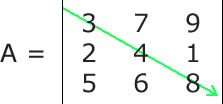 Nesta dica veremos como calcular a soma dos valores dos elementos da diagonal principal de uma matriz usando PHP. Para isso, só precisamos manter em mente que a diagonal principal de uma matriz A é a coleção das entradas Aij em que i é igual a j. Assim, tudo que temos a fazer é converter essa regra para código PHP. Veja um trecho de código PHP completo no qual pedimos para o usuário informar os elementos da matriz e em seguida mostramos a soma dos elementos da diagonal superior:
<?php
// vamos declarar e construir uma matriz de três linhas
// e três colunas
$matriz = array(
array(3, 7, 9),
array(2, 4, 1),
array(5, 6, 8)
);
// guarda a soma dos elementos na diagonal principal
$soma_diagonal = 0;
// vamos mostrar a matriz da forma que ela
// foi informada
echo "<br>";
// percorre as linhas
for($i = 0; $i < count($matriz); $i++){
// percorre as colunas
for($j = 0; $j < count($matriz[0]); $j++){
echo $matriz[$i][$j] . " ";
}
// passa para a próxima linha da matriz
echo "<br>";
}
// vamos calcular a soma dos elementos da diagonal
// principal
for($i = 0; $i < count($matriz); $i++){
for($j = 0; $j < count($matriz[0]); $j++){
if($i == $j){
$soma_diagonal = $soma_diagonal + $matriz[$i][$j];
}
}
}
// finalmente mostramos a soma da diagonal principal
echo "<br>A soma dos elementos da diagonal principal é: "
. $soma_diagonal;
?>
Ao executar este código PHP nós teremos o seguinte resultado: 3 7 9 2 4 1 5 6 8 A soma dos elementos da diagonal principal é: 15 |
Python ::: Dicas & Truques ::: Data e Hora |
Como calcular a diferença de dias entre duas datas em PythonQuantidade de visualizações: 1561 vezes |
|
Nesta dica mostrarei como podemos usar retornar a diferença de dias entre duas datas na linguagem Python usando o objeto Date, do módulo DateTime. Note o uso do construtor date() para construir as duas datas e em seguida passamos estas duas datas para uma função personalizada numero_dias(), que retorna a quantidade de dias entre elas. Veja o código completo para o exemplo:
# vamos importar o objeto Date
from datetime import date
def main():
# vamos criar a data inicial e a data final
d1 = date(2022, 11, 10)
d2 = date(2022, 12, 23)
# vamos calcular a diferença de dias
diferenca = numero_dias(d1, d2)
# e mostramos o resultado
print("A primeira data é: {0}".format(d1))
print("A segunda data é: {0}".format(d2))
print("A diferença de dias entre as duas datas é: {0} dias".format(
diferenca))
# função que recebe duas datas e retorna a diferença
# de dias entre elas
def numero_dias(data1, data2):
return (data2 - data1).days
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: A primeira data é: 2022-11-10 A segunda data é: 2022-12-23 A diferença de dias entre as duas datas é: 43 dias |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Python - Exercício Resolvido de Python NumPy - Como somar duas matrizes usando a biblioteca NumPy do Python Firebird - Como usar o tipo de dados BLOB do Firebird para a gravação de imagens, vídeos e arquivos de música Java - Como calcular o coeficiente angular de uma reta em Java dados dois pontos no plano cartesiano Python - Como converter Metros Quadrados em Quilômetros Quadrados em Python - Python para Física e Engenharia |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






