Java ::: Coleções (Collections) ::: Vector |
Java Collections - Como remover um determinado elemento de um Vector baseado em seu valorQuantidade de visualizações: 11846 vezes |
Muitas vezes precisamos excluir um determinado elemento de um Vector baseado em seu valor. Isso pode ser feito com o método remove(). Veja sua assinatura:public boolean remove(Object o)
import java.util.*;
public class Estudos{
public static void main(String args[]){
// Cria o Vector
Vector<String> nomes = new Vector<String>();
// adiciona itens ao Vector
nomes.addElement("Osmar");
nomes.addElement("Marcos");
nomes.addElement("Ingrid");
// vamos exibir os elementos
for(String nome : nomes)
System.out.println(nome);
// vamos excluir o elemento "Ingrid"
boolean sucesso = nomes.remove("Ingrid");
if(sucesso)
System.out.println("\nO elemento foi removido " +
"com sucesso.\n");
else
System.out.println("\nO elemento NAO foi removido " +
"com sucesso.\n");
// vamos exibir os elementos novamente
for(String nome : nomes)
System.out.println(nome);
}
}
Ao executar este exemplo nós teremos o seguinte resultado: Osmar Marcos Ingrid O elemento foi removido com sucesso. Osmar Marcos |
LISP ::: LISP para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como converter Coordenadas Cartesianas para Coordenadas Polares em LISP - LISP para EngenhariaQuantidade de visualizações: 700 vezes |
|
Nesta nossa série de LISP e AutoLISP para Geometria Analítica e Álgebra Linear, mostrarei um código 100% funcional para fazer a conversão entre coordenadas cartesianas e coordenadas polares. Esta operação é muito frequente em computação gráfica e é parte integrante das disciplinas dos cursos de Engenharia (com maior ênfase na Engenharia Civil). Na matemática, principalmente em Geometria e Trigonometria, o sistema de Coordenadas no Plano Cartesiano, ou Espaço Cartesiano, é um sistema que define cada ponto em um plano associando-o, unicamente, a um conjuntos de pontos numéricos. Dessa forma, no plano cartesiano, um ponto é representado pelas coordenadas (x, y), com o x indicando o eixo horizontal (eixo das abscissas) e o y indicando o eixo vertical (eixo das ordenadas). Quando saímos do plano (espaço 2D ou R2) para o espaço (espaço 3D ou R3), temos a inclusão do eixo z (que indica profundidade). Já o sistema de Coordenadas Polares é um sistema de coordenadas em duas dimensões no qual cada ponto no plano é determinado por sua distância a partir de um ponto de referência conhecido como raio (r) e um ângulo a partir de uma direção de referência. Este ângulo é normalmente chamado de theta (__$\theta__$). Assim, um ponto em Coordenadas Polares é conhecido por sua posição (r, __$\theta__$). Antes de prosseguirmos, veja uma imagem demonstrando os dois sistemas de coordenadas: 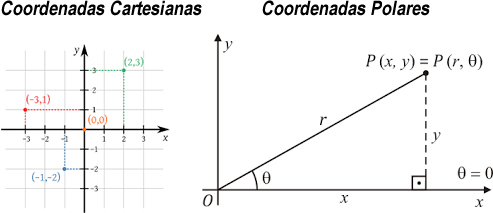 A fórmula para conversão de Coordenadas Cartesianas para Coordenadas Polares é: __$r = \sqrt{x^2+y2}__$ __$\theta = \\arctan\left(\frac{y}{x}\right)__$ E aqui está o código LISP completo que recebe as coordenadas cartesianas (x, y) e retorna as coordenadas polares (r, __$\theta__$):
; programa LISP que converte Coordenadas Cartesianas
; em Coordenadas Polares
(let((x)(y)(raio)(theta)(angulo_graus))
; vamos ler as coordenadas cartesianas
(princ "Valor de x: ")
(force-output)
(setq x (read))
(princ "Valor de y: ")
(force-output)
(setq y (read))
; vamos calcular o raio
(setq raio (sqrt (+ (expt x 2) (expt y 2))))
; agora calculamos o theta (ângulo) em radianos
(setq theta (atan y x))
; queremos o ângulo em graus também
(setq angulo_graus (* 180 (/ theta pi)))
; e exibimos o resultado
(princ "As Coordenadas Polares são: ")
(format t "raio = ~F, theta = ~F, ângulo em graus: ~F"
raio theta angulo_graus)
)
Ao executar este código LISP nós teremos o seguinte resultado: Valor de x: -1 Valor de y: 1 As Coordenadas Polares são: raio = 1.4142135623730951, theta = 2.356194490192345, ângulo em graus = 135.0 Veja que as coordenadas polares equivalentes são (__$\sqrt{2}__$, __$\frac{3\pi}{4}__$), com o theta em radianos. Sim, os professores das disciplinas de Geometria Analítica e Álgebra Linear, Física e outras gostam de escrever os resultados usando raizes e frações em vez de valores reais. |
Python ::: PyQt GUI Toolkit ::: QMainWindow |
Como criar a janela principal de uma aplicação Python PyQt usando a classe QMainWindowQuantidade de visualizações: 1453 vezes |
|
Em geral toda aplicação GUI, ou seja, uma aplicação de interface visual, rodando no Window, Linux, MAC, etc, possui uma janela principal. No PyQt tal janela é criada como uma instância da classe QMainWindow. Veja a posição desta classe na hierarquia de classes do PyQt:
QObject, QPaintDevice
QWidget
QMainWindow
Uma janela QMainWindow possui o seu próprio layout, no qual podemos adicionar uma barra de ferramentas QToolBar, um QDockWidget (que serve para controles que "grudam" em lados diferentes da tela), uma barra de menus QMenuBar e uma barra de status QStatusBar. O layout oferecido pela classe QMainWindow possui uma área central que pode ser ocupada por qualquer tipo de controle visual. É nessa área central que podemos colocar outros tipos de gerenciadores de layouts, que servirão como containers para os componentes visuais da aplicação. Veja uma aplicação PyQt completa na qual temos uma janela principal QMainWindow e um botão QPushButton. Observe como tiramos proveito da programação orientada em Python para criar uma classe JanelaPrincipal que herda de QMainWindow:
# vamos importar os módulos necessários
import sys
from PyQt6.QtCore import *
from PyQt6.QtGui import *
from PyQt6.QtWidgets import *
# vamos criar uma classe que herda de QMainWindow
class JanelaPrincipal(QMainWindow):
# construtor da classe
def __init__(self):
super().__init__()
# definimos o título da janela
self.setWindowTitle("Cadastro de Produtos")
# vamos criar um botão QPushButton
botao = QPushButton("Novo Produto")
# definimos este botão como o controle central
# da janela principal
self.setCentralWidget(botao)
if __name__== "__main__":
# cria a aplicação
app = QApplication(sys.argv)
# cria a janela principal e a coloca visível
janela_principal = JanelaPrincipal()
janela_principal.show()
# executa a aplicação
app.exec()
|
Java ::: Dicas & Truques ::: Formulários e Janelas |
Java Swing para iniciantes - Como adicionar componentes à janela do aplicativo Java SwingQuantidade de visualizações: 16079 vezes |
|
Embora já exista ferramentas de programação que facilitem bastante a construção de interfaces gráficas, principalmente o editor GUI visual do NetBeans, é importante saber como componentes visuais são adicionados à janela da aplicação Java Swing. Veja, por exemplo, a imagem a seguir:  E aqui está o código Java Swing completo a sua criação:
package arquivodecodigos;
import java.awt.*;
import javax.swing.*;
public class Estudos extends JFrame{
public Estudos() {
super("Minha primeira aplicação GUI");
// obtém o painel de conteúdo e adiciona
// um botão à janela
JButton btn = new JButton("Clique Aqui");
getContentPane().add(btn, BorderLayout.NORTH);
setSize(350, 250);
setVisible(true);
}
public static void main(String args[]){
Estudos app = new Estudos();
app.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
}
}
|
Python ::: Python para Engenharia ::: Engenharia Civil - Concreto, Concreto Armado e Concretos Especiais |
Como calcular a armadura mínima de tração de uma viga de concreto armado usando Python - Python para Engenharia CivilQuantidade de visualizações: 141 vezes |
|
De acordo com a ABNT NBR 6118 (Projeto de estruturas de concreto armado), a armadura de tração, em elementos estruturais armados ou protendidos deve ser determinada pelo dimensionamento da seção a um determinado momento fletor mínimo, respeitada a taxa mínima absoluta ρmin de 0,15%. Dessa forma, a área de aço mínima levando em consideração a taxa mínima absoluta ρmin de 0,15% de armadura longitudinal para as vigas de concreto armado usando concreto com FCK até 30 Mpa é calculada pela seguinte fórmula: \[A_\text{s,min} = \frac{0,15}{100} \cdot A_\text{c}\] Onde: As,min é a área da armadura mínima de aço em cm2; Ac é a área de concreto em cm2, ou seja, a largura bw da viga multiplicada por sua altura h (ambas em cm). Veja agora o código Python completo que lê a largura, a altura da viga, o FCK do concreto (no código eu tratei FCK até 50 Mpa) e mostra a área mínima da armadura de aço e sugestões das barras a serem usadas:
# vamos importar o módulo Math
import math
# função usada para calcular e retornar a quantidade
# de barras de aço de acordo com a área de aço (considerando
# aço CA-50)
def quant_barras(area_aco):
# barras de 6.3mm (o mínimo aceitável pela NBR 6118)
quantidade_6_3 = math.ceil(area_aco / 0.31)
quantidade_8 = math.ceil(area_aco / 0.5) # barras de 8mm
quantidade_10 = math.ceil(area_aco / 0.785) # barras de 10mm
quantidade_12_5 = math.ceil(area_aco / 1.22) # barras de 12.5mm
# mostra as sugestões de quantidade de barras
if (quantidade_6_3) > 1:
print("{0} barras de 6.3 mm".format(quantidade_6_3))
if (quantidade_8) > 1:
print("{0} barras de 8 mm".format(quantidade_8))
if (quantidade_10) > 1:
print("{0} barras de 10 mm".format(quantidade_10))
if (quantidade_12_5) > 1:
print("{0} barras de 12.5 mm".format(quantidade_12_5))
# função principal do programa Python
def main():
# vamos pedir para o usuário informar a altura da viga
altura = float(input("Informe a altura h da viga em cm: "))
# vamos pedir para o usuário informar a largura da viga
largura = float(input("Informe a largura bw da viga em cm: "))
# vamos pedir para o usuário informar o FCK do concreto
fck = float(input("Informe o FCK do concreto em Mpa: "))
# vamos calcular o pmin de acordo com o FCK informado
if (fck <= 30):
pmin = 0.15
elif (fck == 35):
pmin = 0.164
elif (fck == 40):
pmin = 0.179
elif (fck == 45):
pmin = 0.194
else:
pmin = 0.208
# já temos o pmin, vamos calcular a área mínima de aço
area_concreto = largura * altura
as_min = (pmin / 100.0) * area_concreto
# vamos mostrar os resultados
print("\nA área da armadura mínima longitudinal é: {0} cm2".format(
round(as_min, 5)))
# mostra as sugestões de barras
print("\nSugestões de barras:\n-------------------------")
quant_barras(as_min)
if __name__ == "__main__":
main()
Ao executarmos este código Python nós teremos o seguinte resultado: Informe a altura h da viga em cm: 50 Informe a largura bw da viga em cm: 20 Informe o FCK do concreto em Mpa: 30 A área da armadura mínima é: 1.5 cm2 Sugestões de barras: ------------------------- 5 barras de 6.3 mm 3 barras de 8 mm 2 barras de 10 mm 2 barras de 12.5 mm |
Python ::: Dicas & Truques ::: Strings e Caracteres |
Como contar as ocorrências de uma substring em uma string Python usando a função count()Quantidade de visualizações: 10097 vezes |
Em várias ocasiões nós precisamos obter a quantidade de vezes que parte de uma palavra é encontrada em outra palavra, frase ou texto, ou seja, uma substring dentro de uma string. Para isso nós podemos usar o método count() da linguagem Python. Veja sua assinatura:count(substring[, início[, fim]]) Veja um código Python completo para este exemplo:
# função principal do programa
def main():
frase = "Gosto de Python porque Python é muito bom"
# conta as ocorrências de "Python"
print("\"Python\" ocorreu", frase.count("Python"), "vezes.")
if __name__== "__main__":
main()
Ao executar este código nós teremos o seguinte resultado: "Python" ocorreu 2 vezes. |
wxWidgets ::: Dicas & Truques ::: wxApp |
Como usar a classe wxApp em suas aplicações C++ wxWidgetsQuantidade de visualizações: 1870 vezes |
|
A classe wxApp (Application Class) é uma das primeiras classes que devemos estudar se quisermos ter um domínio perfeito do framework wxWidgets. Para usá-la, devemos incluir #include <wx/app.h> em nossos códigos. Essa classe herda de wxAppConsole. Todas as aplicações wxWidgets definem uma classe application derivada de wxApp. Há somente uma instância dela, e essa instância representa a aplicação sendo executada no momento. De todos os métodos herdados de wxApp, há pelo menos um que devemos implementar, e ele é a função OnInit(), que é chamada quando o wxWidgets está pronto para executar o nosso código. OnInit() equivale ao main() em C/C++ ou WinMain (aplicações Win32). Veja um trecho de código no qual declaramos e usamos a classe wxApp: Código para aplicacao.h:
#include <wx/wx.h>
// arquivo de definição
// declaramos a classe application
class MinhaAplicacao : public wxApp{
public:
// é chamado no startup da aplicação
virtual bool OnInit();
};
// declara MinhaAplicacao& GetApp()
DECLARE_APP(MinhaAplicacao)
Código para aplicacao.cpp:
#include "aplicacao.h"
// arquivo de implementação
// aqui o wxWidgets implementa nosso objeto MinhaAplicacao
IMPLEMENT_APP(MinhaAplicacao)
bool MinhaAplicacao::OnInit(){
// vamos mostrar uma mensagem ao iniciar a aplicação
wxMessageDialog *alerta = new wxMessageDialog(NULL,
wxT("A aplicação foi iniciada com sucesso"), wxT("Informação"), wxOK);
alerta->ShowModal();
// em geral retornamos true para iniciar o loop de eventos
// mas essa aplicação exibe apenas uma janela de mensagem. Podemos sair
return false;
}
Veja que no arquivo de declaração (header file) nós temos a macro DECLARE_APP. Ela nos permite declarar a função wxGetApp() que retorna uma referência para o objeto aplicação. Se não fizermos isso, a única forma de obter tal referência é usando o ponteiro global wxTheApp, que é do tipo wxApp*. A macro IMPLEMENT_APP, no arquivo de implementação, permite ao wxWidgets criar dinamicamente uma instância do objeto application no ponto apropriado da inicialização da biblioteca. Esse trecho de código é totalmente funcional, mas teremos apenas a exibição de uma mensagem wxMessageDialog. Por essa razão eu retornei false no laço de eventos. Se tivéssemos criado uma janela wxFrame, o retorno deveria ser true, já que teríamos de lidar com eventos. Para finalizarmos, lembre-se de que o método OnInit() da classe wxApp é o local ideal para se fazer as verificações iniciais da aplicação, tais como conexão com banco de dados, permissão do usuário, disponibilidade da rede, etc. |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de Java - Declarar e construir um vetor, pedir ao usuário para informar os valores dos elementos e mostrar o maior e o menor valor armazenado no vetorQuantidade de visualizações: 10194 vezes |
|
Pergunta/Tarefa: Escreva um programa Java GUI ou console que declara e constrói um vetor de 10 inteiros. Em seguida peça ao usuário para informar os valores para os elementos do vetor e, uma vez preenchida, percorra o vetor e mostre os valores armazenados. Para finalizar varra o vetor novamente e mostre os valores do maior e do menor elemento. Sua saída deverá ser parecida com: Informe o 1º valor: 8 Informe o 2º valor: 3 Informe o 3º valor: 4 Informe o 4º valor: 1 Informe o 5º valor: 6 Informe o 6º valor: 5 Informe o 7º valor: 7 Informe o 8º valor: 2 Informe o 9º valor: 3 Informe o 10º valor: 8 Os valores informados foram: 8 3 4 1 6 5 7 2 3 8 O maior valor é: 8 O menor valor é: 1 Veja a resolução comentada deste exercício usando Java console:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
Scanner entrada = new Scanner(System.in);
// declara e constrói um vetor de 10 inteiros
int valores[] = new int[10];
// vamos pedir ao usuário para informar os 10 valores
for(int i = 0; i < valores.length; i++){
System.out.print("Informe o " + (i + 1) + "º valor: ");
valores[i] = Integer.parseInt(entrada.nextLine());
}
// vamos exibir os valores informados
System.out.println("\nOs valores informados foram: ");
for(int i = 0; i < valores.length; i++){
System.out.print(valores[i] + " ");
}
// agora vamos encontrar o maior e o menor valor no vetor
// vamos assumir que o primeiro elemento
// possui o maior e o menor valor
int maior = valores[0], menor = valores[0];
for(int i = 0; i < valores.length; i++){
// encontra o maior valor
if(valores[i] > maior){
maior = valores[i];
}
// encontra o menor valor
if(valores[i] < menor){
menor = valores[i];
}
}
System.out.println("\n\nO maior valor é: " + maior);
System.out.println("O menor valor é: " + menor);
}
}
Uma idéia na resolução deste exercício é assumir que o primeiro elemento do vetor possui tanto o maior quanto o menor valor. |
C# ::: Coleções (Collections) ::: List<T> |
Como percorrer os itens de uma List do C# usando o laço forQuantidade de visualizações: 558 vezes |
|
Em várias ocasiões nós precisamos percorrer os elementos de uma lista do C#. Para isso nós podemos usar o laço for e, dentro deste laço, acessar os elementos da lista individualmente usando o operador [] e o índice desejado. Veja o código C# completo para o exemplo:
using System;
using System.Collections.Generic;
namespace Estudos {
class Principal {
static void Main(string[] args) {
List<int> valores = new List<int>();
// insere valores na lista
valores.Add(4);
valores.Add(2);
valores.Add(87);
valores.Add(23);
valores.Add(100);
// agora vamos usar o laço for para percorrer os
// itens da lista
Console.WriteLine("Os itens da lista são:");
for(int i = 0; i < valores.Count; i++) {
Console.Write(valores[i] + ", ");
}
Console.WriteLine("\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Os itens da lista são: 4, 2, 87, 23, 100, |
GoLang ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas |
Como calcular a equação reduzida da reta em GoLang dados dois pontos pertencentes à retaQuantidade de visualizações: 984 vezes |
|
Nesta dica de Go veremos como calcular a equação reduzida da reta quando temos dois pontos pertencentes à esta reta. Não, nessa dica não vamos calcular a equação geral da reta, apenas a equação reduzida. Em outras dicas do site você encontra como como isso pode ser feito. Para relembrar: a equação reduzida da reta é y = mx + n, em que x e y são, respectivamente, a variável independente e a variável dependente; m é o coeficiente angular, e n é o coeficiente linear. Além disso, m e n são números reais. Com a equação reduzida da reta, é possível calcular quais são os pontos que pertencem a essa reta e quais não pertencem. Vamos começar então analisando a seguinte figura, na qual temos dois pontos que pertencem à uma reta: 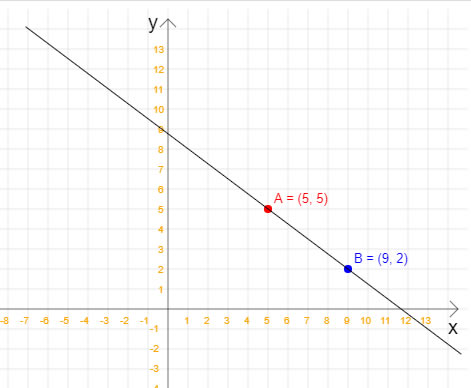 Note que a reta da figura passa pelos pontos A(5, 5) e B(9, 2). Então, uma vez que já temos os dois pontos, já podemos calcular a equação reduzida da reta. Veja o código GoLang completo para esta tarefa:
// pacote principal
package main
// vamos importar o módulo de formatação de
// entrada e saída
import "fmt"
// esta é a função principal do programa
func main() {
// variáveis que vamos usar na resolução do problema
var x1, y1, x2, y2, m, n float32
var sinal string
// vamos ler as coordenadas do primeiro ponto
fmt.Print("Coordenada x do primeiro ponto: ")
fmt.Scanln(&x1)
fmt.Print("Coordenada y do primeiro ponto: ")
fmt.Scanln(&y1)
// vamos ler as coordenadas do segundo ponto
fmt.Print("Coordenada x do segundo ponto: ")
fmt.Scanln(&x2)
fmt.Print("Coordenada y do segundo ponto: ")
fmt.Scanln(&y2)
sinal = "+"
// vamos calcular o coeficiente angular da reta
m = (y2 - y1) / (x2 - x1)
// vamos calcular o coeficiente linear
n = y1 - (m * x1)
// coeficiente linear menor que zero? O sinal será negativo
if n < 0 {
sinal = "-"
n = n * -1
}
// mostra a equação reduzida da reta
fmt.Printf("Equação reduzida: y = %.2fx %s %.2f",
m, sinal, n);
}
Ao executar este código GoLang nós teremos o seguinte resultado: Coordenada x do primeiro ponto: 5 Coordenada y do primeiro ponto: 5 Coordenada x do segundo ponto: 9 Coordenada y do segundo ponto: 2 Equação reduzida: y = -0,75x + 8,75 Para testarmos se nossa equação reduzida da reta está realmente correta, considere o valor 3 para o eixo x da imagem acima. Ao efetuarmos o cálculo: >> y = (-0.75 * 3) + 8.75 y = 6.5000 temos o valor 6.5 para o eixo y, o que faz com que o novo ponto caia exatamente em cima da reta considerada na imagem. |
Nossas 20 dicas & truques de programação mais populares |
|
Delphi - Como obter a quantidade de caracteres em uma palavra ou texto usando a função Length() do Delphi Python - Como criar arrays (vetores e matrizes) usando o objeto ndarray da biblioteca Numpy do Python |
Você também poderá gostar das dicas e truques de programação abaixo |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






