Você está aqui: Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Como testar se uma matriz é uma Matriz Triangular Superior em Java - Exercícios Resolvidos de JavaQuantidade de visualizações: 619 vezes |
|
Pergunta/Tarefa: Uma Matriz Triangular Superior é a matriz na qual todos os termos que estão abaixo da diagonal principal são iguais a zero e os termos que estão acima da diagonal principal são números reais. Veja um exemplo de Matriz Triangular Superior na imagem abaixo: 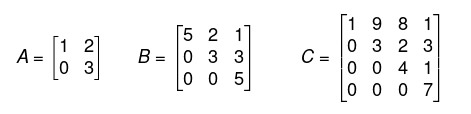 Escreva um programa Java que pede para o usuário informar o número de linhas e colunas de uma matriz quadrada. Em seguida solicite os valores para cada um dos elementos da matriz. Para finalizar informe ao usuário se a matriz informada é uma matriz triangular superior. Sua saída deverá ser parecida com:
Número de linhas e colunas da matriz: 3
Valor para a linha 0 e coluna 0: 8
Valor para a linha 0 e coluna 1: 2
Valor para a linha 0 e coluna 2: 3
Valor para a linha 1 e coluna 0: 0
Valor para a linha 1 e coluna 1: 3
Valor para a linha 1 e coluna 2: 9
Valor para a linha 2 e coluna 0: 0
Valor para a linha 2 e coluna 1: 0
Valor para a linha 2 e coluna 2: 2
Valores na matriz
8 2 3
0 3 9
0 0 2
A matriz é uma matriz triangular superior
Veja a resolução comentada deste exercício usando Java:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
// para ler a entrada do usuário
Scanner entrada = new Scanner(System.in);
// vamos pedir a ordem da matriz
System.out.print("Número de linhas e colunas da matriz: ");
int ordem = Integer.parseInt(entrada.nextLine());
// agora vamos construir a matriz
int matriz[][] = new int[ordem][ordem];
// vamos ler os valores para os elementos da matriz
System.out.println();
for(int i = 0; i < ordem; i++){ // linhas
for(int j = 0; j < ordem; j++){ // colunas
System.out.print("Valor para a linha " + i + " e coluna " + j + ": ");
matriz[i][j] = Integer.parseInt(entrada.nextLine());
}
}
// vamos mostrar a matriz da forma que ela foi informada
System.out.println("\nValores na matriz\n");
for(int i = 0; i < ordem; i++){
for(int j = 0; j < ordem; j++){
System.out.printf("%5d ", matriz[i][j]);
}
// passa para a próxima linha da matriz
System.out.println();
}
// agora vamos testar se a matriz é uma matriz triangular
// superior
boolean triangular_superior = true;
for(int i = 0; i < ordem; i++){
for(int j = 0; j < ordem; j++){
// a condição para que a matriz seja triangular superior é
// que os elementos abaixo da diagonal principal sejam
// iguais a zero
if((j < i) && (matriz[i][j] != 0)){
triangular_superior = false;
}
}
}
if(triangular_superior){
System.out.println("\nA matriz é uma matriz triangular superior");
}
else{
System.out.println("\nA matriz não é uma matriz triangular superior");
}
}
}
Listamos abaixo algumas propriedades específicas da matriz triangular. 1) o determinante de uma matriz triangular é igual ao produto dos termos da diagonal principal. 2) o produto entre duas matrizes triangulares é uma matriz triangular. 3) se um dos termos da diagonal principal da matriz triangular for igual a zero, então o seu determinante será igual a zero e, consequentemente, ela não será inversível. 4) a matriz inversa de uma matriz triangular é também uma matriz triangular. 5) a soma de duas matrizes triangulares superiores é uma matriz triangular superior; de forma análoga, a soma de duas matrizes triangulares inferiores é uma matriz triangular inferior. |
|
|
Mais Desafios de Programação e Exercícios e Algoritmos Resolvidos de Java |
Veja mais Dicas e truques de Java |
Dicas e truques de outras linguagens |
|
VB.NET - Como retornar a versão do .NET a partir de seus códigos VB.NET usando Environment.Version.ToString() |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






