Ofereço ajuda em Java, C/C++, Python, C#, LISP, AutoLisp, AutoCAD
Ofereço ajuda em PHP, Python, C#, JavaScript, Laravel, Google Ads e SEO
Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica.
Java ::: Tratamento de Erros ::: Passos Iniciais

Quais as diferenças entre checked exceptions, runtime exceptions e errors na linguagem Java?

Quantidade de visualizações: 15693 vezes
Checked exceptions (exceções verificadas), runtime exceptions (exceções de tempo de execução) e errors (erros) possuem diferenças importantes e devem ser entendidas perfeitamente para tirarmos maior proveito da plataforma Java.

Entre as checked exceptions podemos citar FileNotFoundException, ClassNotFoundException e IOException. Agora veja: problemas tais como um arquivo não encontrado, uma classe não encontrada ou problemas com entrada e saída (talvez a impressora parou de responder ou a rede caiu) fogem completamente do domínio da aplicação. Tais exceções não são provocadas por código mal escrito ou mal testado. Desta forma, o Java força que todas as checked exceptions estejam em um bloco try...catch. Vamos ver se isso é verdade? Observe o trecho de código abaixo:

import java.io.*;

public class Estudos{
  public static void main(String[] args){
    DataInputStream in = new DataInputStream(
      new BufferedInputStream(
        new FileInputStream("conteudo.txt")));
        
    while(in.available() != 0)
      System.out.print((char) in.readByte());
    
    System.exit(0);
  }
}

Se tentarmos compilar este código teremos o seguinte resultado:

Estudos.java:7: unreported exception 
java.io.FileNotFoundException; must be caught 
or declared to be thrown
  new FileInputStream("conteudo.txt")));
  ^
Estudos.java:9: unreported exception 
java.io.IOException; must be caught or 
declared to be thrown
  while(in.available() != 0)
           ^
Estudos.java:10: unreported exception 
java.io.IOException; must be caught or 
declared to be thrown
  System.out.print((char) in.readByte());
                             ^
3 errors


Aqui nós temos uma exceção FileNotFoundException e duas exceções IOException. Vamos nos concentrar na exceção gerada pelo construtor da classe FileInputStream. Folheando a documentação do Java nós encontramos:

public FileInputStream(String name)
  throws FileNotFoundException


É aqui que as coisas começam a ficar interessantes. Todos os métodos Java que podem atirar exceções verificadas são marcados com throws e o tipo de exceção lançada. A palavra throws é usada para transferir a responsabilidade do tratamento do erro para o chamador de tais métodos. Outro exemplo é o método readByte() da classe DataInputStream:

public final byte readByte()
  throws IOException


Para corrigir as exceções acima, só precisamos usar um bloco try...catch. Veja:

import java.io.*;

public class Estudos{
  public static void main(String[] args){
    try{
      DataInputStream in = new DataInputStream(
        new BufferedInputStream(
          new FileInputStream("conteudo.txt")));
        
      while(in.available() != 0)
        System.out.print((char) in.readByte());
    } 
    catch(IOException e){
      System.out.print(e.getMessage());
    }

    System.exit(0);
  }
}

Exceções verificadas são todas aquelas que descendem de Exception mas não descendem de RuntimeException.

As exceções de tempo de execução (runtime exceptions) são provocadas por código mal escrito ou mal testado, ou seja, são causadas por nós programadores. Entre estas exceções podemos citar ArithmeticException, IndexOutOfBoundsException e NoSuchElementException. De fato, um erro aritmético é responsabilidade do programador, pois cabe a este verificar se os valores estão dentro da faixa permitida por cada tipo de dados.

Ao contrário das exceções verificadas, o compilador não força o uso do bloco try...catch para as runtime exceptions. De fato, isso é fácil de compreender, uma vez que tais exceções não deveriam jamais aparecer.

Contudo, pode ser desejável usar o bloco try...catch em casos em que os valores de uma operação são definidos pelo usuário. Veja um exemplo:

import java.util.*;

public class Estudos{
  public static void main(String[] args){
    Scanner in = new Scanner(System.in);
    
    System.out.print("Informe um inteiro: ");
    int valor = in.nextInt();

    System.out.print("Informe outro inteiro: ");
    int valor2 = in.nextInt();

    System.out.println("O resultado é " + 
      valor / valor2);
  }
}

Se executarmos este código e informarmos o valor 0 para o segundo inteiro, teremos a seguinte exceção:

Informe um inteiro: 4
Informe outro inteiro: 0
Exception in thread "main" 
  java.lang.ArithmeticException: / by zero
  at Estudos.main(Estudos.java:13)


Uma forma de corrigir isso é testando os valores informados para verificar suas faixas ou lançar uma exceção. Veja como usamos esta última alternativa:

import java.util.*;

public class Estudos{
  public static void main(String[] args){
    Scanner in = new Scanner(System.in);
    
    System.out.print("Informe um inteiro: ");
    int valor = in.nextInt();

    System.out.print("Informe outro inteiro: ");
    int valor2 = in.nextInt();

    try{
      System.out.println("O resultado é " + 
        valor / valor2);
    }
    catch(ArithmeticException e){
      System.out.println("Uma exceção " +
       "ArithmeticException ocorreu, " +
       "possivelmente uma tentativa de " +
       "divisão por zero.");
    }
  }
}

Agora se informarmos zero para o segundo inteiro, teremos:

Informe um inteiro: 5
Informe outro inteiro: 0
Uma exceção ArithmeticException ocorreu, 
possivelmente uma tentativa de divisão
por zero.


As runtime exceptions (causadas por falha nossa, os programadores) descedem de java.lang.RuntimeException.

Além das runtime exceptions e das checked exceptions, temos também os errors, que descedem de java.lang.Error e não devem jamais ser atirados ou tratados em blocos try...catch. Este tipo de erro é reservado para indicar problema na JVM. Entre tais erros temos OutOfMemoryError, que é lançado quando a Java Virtual Machine não consegue alocar um objeto porque sua fatia de memória esgotou e o Garbage Collector ainda não liberou mais memória. Não há razão para tratarmos isso em um bloco try...catch uma vez que, ao contrário de C++, a liberação de memória só é feita pelo GC. O melhor a fazer é deixar mesmo o programa ser encerrado e encontrar alternativas para a correção do problema.

Java ::: Estruturas de Dados ::: Árvore Binária e Árvore Binária de Busca

Estruturas de Dados em Java - Como obter o nó com menor valor em uma árvore binária de busca em Java

Quantidade de visualizações: 3529 vezes
Em exemplos dessa seção nós vimos como criar árvores binárias e árvores binárias de busca em Java e como pesquisar ou fazer a sua travessia, visitando cada um dos nós. Nesta dica mostrarei como obter o nó com o menor valor em uma árvore binária. O truque aqui é descer o lado esquerdo da árvore até o último nó. Veja:

// método que permite retornar o menor nó de uma árvore
// binária de busca
public No retornarMenorElemento(){
  // chama a versão recursiva do método
  return retornarMenorElemento(raiz);
}
  
public No retornarMenorElemento(No no){
  if((no == null) || (no.getEsquerdo() == null)){
    return no; // ponto de parada
  }
  else{ // vamos continuar descendo do lado esquerdo
    return retornarMenorElemento(no.getEsquerdo());
  }
}

Este método faz parte da classe ArvoreBinariaBusca.java. Veja agora como chamá-lo a partir da classe principal, ou seja, a classe de teste:

package arvore_binaria;

import java.util.Scanner;

public class ArvoreBinariaTeste {
  public static void main(String[] args) {
    Scanner entrada = new Scanner(System.in);  
       
    // vamos criar um novo objeto da classe ArvoreBinariaBusca
    ArvoreBinariaBusca arvore = new ArvoreBinariaBusca();
    
    // vamos inserir 5 valores na árvore
    for(int i = 0; i < 5; i++){
      System.out.print("Informe um valor inteiro: ");
      int valor = Integer.parseInt(entrada.nextLine());
       
      // vamos inserir o nó e verificar o sucesso da operação
      if(!arvore.inserir(valor)){
        System.out.println("Não foi possível inserir." +
          " Um elemento já contém este valor.");  
      }
    }
     
    // vamos o menor elemento na árvore binária de busca
    System.out.println("\nO menor nó é: " + 
      arvore.retornarMenorElemento().getValor());
     
    System.out.println("\n");
  }
}

Ao executar este código teremos o seguinte resultado:

Informe um valor inteiro: 5
Informe um valor inteiro: 12
Informe um valor inteiro: 87
Informe um valor inteiro: 1
Informe um valor inteiro: 3

O menor nó é: 1


Python ::: Python para Engenharia ::: Engenharia Civil - Concreto, Concreto Armado e Concretos Especiais

Cálculo de estribos em vigas de concreto armado usando Python - Verificação da compressão diagonal do concreto

Quantidade de visualizações: 332 vezes
No dimensionamento de vigas de concreto armado à força cortante, ou seja, aos esforços de cisalhamento, nós adotamos, de acordo com recomendações da ABNT NBR 6118 (Projeto de estruturas de concreto armado), o modelo de treliça clássica de Ritter-Mörsh, na qual é suposto que uma carga aplicada num ponto qualquer de uma viga de concreto armado, chegue até os apoios percorrendo o caminho de uma treliça. Recordemos ainda que na treliça clássica de Ritter-Mörsh o ângulo de inclinação das bielas comprimidas é igual à 45°.

Neste modelo de treliça, a compressão do banzo superior é resistida pelo concreto, enquanto a tração do banzo inferior é resistida pelo aço. As diagonais comprimidas também são resistidas pelo concreto, cabendo ao aço (estribos) o papel de reforçar as diagonais tracionadas. Notem que usei "reforçar", pois o concreto oferece também uma parcela de resistência à tração nestas diagonais.

Sendo assim, um dos primeiros passos no cálculo e detalhamento das armaduras transversais, ou seja, a armadura de cisalhamento de uma viga de concreto armado, é a verificação da compressão diagonal do concreto. Neste passo nós verificamos se as bielas comprimidas resistem ao esforço cortante solicitante de projeto VSd.

A verificação da compressão diagonal do concreto no Modelo I (no qual o ângulo &#945;, que é o ângulo entre os estribos e o eixo longitudinal da viga, pode ser considerado entre 45º e 90º) pode ser realizada por meio da seguinte fórmula:

\[V_\text{Rd2} = 0,27 \cdot \alpha_\text{v2} \cdot f_\text{cd} \cdot b_w \cdot d \]
Onde:

fcd é a resistência de cálculo do concreto, em kN/cm2;

bw é a largura da viga, em centímetros;

d é a altura útil da viga em centímetros;

Já o &#945;v2 pode ser calculado pela seguinte fórmula:

\[\alpha_\text{v2} = 1 - \frac{f_\text{ck}}{250}\]
Onde:

fck é a resistência característica do concreto, em Mpa.

Veja agora o código Python :

# método principal
def main():
  # vamos pedir para o usuário informar a altura da viga
  altura = float(input("Informe a altura h da viga em cm: "))
   
  # vamos pedir para o usuário informar a largura da viga
  largura = float(input("Informe a largura bw da viga em cm: "))

  # vamos calcular a altura útil da viga
  # aqui eu usei 0.9 mas alguns engenheiros usam 0.95
  altura_util = 0.9 * altura
  
  # vamos pedir para o usuário informar o FCK do concreto
  fck = float(input("Informe o FCK do concreto em Mpa: "))

  # vamos ler o coeficiente de minoração do concreto
  yc = float(input("Informe o coeficiente de minoração yc: "))   

  # vamos solicitar o esforço cortante solicitante VSk
  VSk = float(input("Informe o esforço cortante solicitante em kN: ")) 

  # vamos ler o coeficiente de majoração das cargas
  yf = float(input("Informe o coeficiente de majoração yf: "))

  # vamos calcular o esforço cortante solicitante de cálculo VSd
  VSd = yf * VSk

  # agora vamos calcular o fcd do concreto
  fcd = fck / yc

  # vamos calcular o alfa v2
  av2 = 1 - (fck / 250)

  # finalmente vamos calcular o VRd2 no Modelo de Cálculo I
  VRd2 = 0.27 * av2 * (fcd / 10) * largura * altura_util 

  # vamos mostrar os resultados
  print("\n------ RESULTADOS -----------------------------")
  print("O fcd do concreto é: {0} Mpa".format(round(fcd, 4)))
  print("O valor de av2 é: {0}".format(round(av2, 4)))
  print("O valor de VRd2 é: {0} kN".format(round(VRd2, 4)))
  print("O valor de VSd é: {0} kN".format(round(VSd, 4)))

  # vamos testar se as bielas de compressão não serão esmagadas
  if (VSd <= VRd2):
    print("VSd <= VRd2: As bielas de compressão RESISTEM")
  else:
    print("VSd > VRd2: As bielas de compressão NÃO RESISTEM")

if __name__ == "__main__":
  main()

Ao executar este código Python nós teremos o seguinte resultado:

Informe a altura h da viga em cm: 40
Informe a largura bw da viga em cm: 20
Informe o FCK do concreto em Mpa: 25
Informe o coeficiente de minoração yc: 1.4
Informe o esforço cortante solicitante em kN: 75
Informe o coeficiente de majoração yf: 1.4

------ RESULTADOS -----------------------------
O fcd do concreto é: 17.8571 Mpa
O valor de av2 é: 0.9
O valor de VRd2 é: 312.4286 kN
O valor de VSd é: 105.0 kN
VSd <= VRd2: As bielas de compressão RESISTEM

C ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes)

Como pesquisar um valor em um vetor de inteiros em C

Quantidade de visualizações: 9506 vezes
Em algumas situações precisamos verificar se um determinado valor está contido em uma matriz de inteiros em C. Nesta dica eu mostro como isso pode ser feito usando a pesquisa ou busca linear. Veja o código completo comentado:

#include <stdio.h>
#include <stdlib.h>

int main(int argc, char *argv[])
{
  // vamos declarar e inicializar uma matriz de cinco inteiros
  int valores[] = {3, 8, 2, 1, 4};
  int encontrei = 0; // vamos inicializar encontrei como falso
  int i; // variável de controle do laço
  
  int valor = 2; // valor a ser pesquisado
  
  // vamos percorrer os elementos da matriz e verificar se o valor
  // informado está contido na mesma
  for(i = 0; i < 5; i++){
    // o valor pesquisado é igual ao valor do elemento atual?
    if(valores[i] == valor){
      encontrei = 1; // encontrei agora é verdadeiro
      break; // vamos sair do laço              
    }      
  }
  
  // vamos mostrar o resultado
  if(encontrei)
    printf("O valor pesquisado esta contido na matriz");
  else
    printf("O valor pesquisado NAO esta contido na matriz");  
  
  printf("\n\n");
  system("pause");
  return 0;
}

Ao executar este trecho de código teremos o seguinte resultado:

O valor pesquisado está contido na matriz.

C++ ::: Dicas & Truques ::: Strings e Caracteres

Como acessar os caracteres de uma string individualmente em C++ usando o operador []

Quantidade de visualizações: 24790 vezes
Em várias situações nós precisamos retornar os caracteres de uma string individualmente, um de cada vez. Para isso nós podemos acessá-los using o operador [] e o índice desejado. Lembre-se de que, em C++, os índices começam sempre em 0.

Veja o código C++ completo para o exemplo:

#include <iostream>
#include <string>

using namespace std;
 
// função principal do programa 
int main(int argc, char *argv[]){
  // vamos criar uma nova string
  string palavra("FACULDADE");
   
  // agora vamos percorrer os caracteres individualmente  
  for(int i = 0; i < palavra.size(); i++){
    cout << palavra[i] << "\n";             
  }
   
  cout << "\n" << endl;
  system("PAUSE"); // pausa o programa
  return EXIT_SUCCESS;
}

Ao executar este código C++ nós teremos o seguinte resultado:

F
A
C
U
L
D
A
D
E

Delphi ::: VCL - Visual Component Library ::: TEdit

Como definir o conteúdo de um TEdit do Delphi em tempo de execução usando a função SendMessage() da API do Windows e a mensagem WM_SETTEXT

Quantidade de visualizações: 11500 vezes
Embora o Delphi já nos forneça as ferramentas necessárias para definir o conteúdo de um TEdit em tempo de execução, é importante saber como realizar esta tarefa usando a API do Windows. Para isso, podemos usar a função SendMessage() em combinação com a mensagem WM_SETTEXT.

A função SendMessage() da API do Windows possui a seguinte assinatura em C/C++:

LRESULT SendMessage(          
  HWND hWnd,
  UINT Msg,
  WPARAM wParam,
  LPARAM lParam
);

No arquivo Windows.pas podemos encontrar o protótipo e corpo desta função convertidos para Object Pascal: 

// Protótipo
{$EXTERNALSYM SendMessage}
function SendMessage(hWnd: HWND; Msg: UINT; wParam: WPARAM; 
  lParam: LPARAM): LRESULT; stdcall;

// Implementação
function SendMessage; external user32 name 'SendMessageW';

Note que precisamos de um HWND (Handle) para a caixa de texto. Feito isso só precisamos enviar a mensagem WM_SETTEXT juntamente com o conteúdo a ser exibido no controle. Veja: 

procedure TForm1.Button1Click(Sender: TObject);
var
  texto: String;
begin
  // conteúdo a ser definido para a caixa de texto
  texto := 'Veja isso';

  // vamos definir o conteúdo usando a função SendMessage
  // fornecendo a mensagem WM_SETTEXT
  SendMessage(Edit1.Handle, WM_SETTEXT, 0, Integer(PChar(texto)));
end;

Veja que o parâmetro wParam da função SendMessage não é usado quando a mensagem é WM_SETTEXT. Desta forma só precisamos fornecer o valor 0.

Python ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas

Como calcular o cateto oposto dadas as medidas da hipotenusa e do cateto adjascente em Python

Quantidade de visualizações: 2864 vezes
Todos estamos acostumados com o Teorema de Pitágoras, que diz que "o quadrado da hipotenusa é igual à soma dos quadrados dos catetos". Baseado nessa informação, fica fácil retornar a medida do cateto oposto quando temos as medidas da hipotenusa e do cateto adjascente. Isso, claro, via programação em linguagem Python.

Comece observando a imagem a seguir:



Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. A medida da hipotenusa é, sem arredondamentos, 36.056 metros.

Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras):

\[c^2 = a^2 + b^2\]

Tudo que temos que fazer é mudar a fórmula para:

\[a^2 = c^2 - b^2\]

Veja que agora o quadrado do cateto oposto é igual ao quadrado da hipotenusa menos o quadrado do cateto adjascente. Não se esqueça de que a hipotenusa é o maior lado do triângulo retângulo.

Veja agora como esse cálculo é feito em linguagem Python:

# vamos importar o módulo Math
import math as math

def main():
  c = 36.056 # medida da hipotenusa
  b = 30 # medida do cateto adjascente
  
  # agora vamos calcular o comprimento da cateto oposto
  a = math.sqrt(math.pow(c, 2) - math.pow(b, 2))
 
  # e mostramos o resultado
  print("A medida do cateto oposto é: %f" % a)
  
if __name__== "__main__":
  main()

Ao executar este código Python nós teremos o seguinte resultado:

A medida do cateto oposto é: 20.000878

Como podemos ver, o resultado retornado com o código Python confere com os valores da imagem apresentada.

HTML5 ::: HTML5 + JavaScript ::: Canvas

Como usar o método arc() do objeto Canvas do HTML5 para desenhar arcos, curvas e círculos

Quantidade de visualizações: 4338 vezes
O método arc() do objeto Canvas do HTML5 nos permite criar figuras tais como arcos, curvas e círculos. Para isso é importante entender os seus parâmetros:

arc(x, y, radius, ang1, ang2, direction);


Os parâmetros x e y indicam as coordenadas do centro do círculo. O parâmetro radius indica o raio do círculo. Os parâmetros ang1 e ang2 indicam o ângulo inicial e o ângulo final. O parâmetro direction indica a direção do desenho. Se o valor true for informado, a direção será anti-horário. Se for false, o desenho será no sentido horário.

É importante observar que os ângulos são medidos em radianos, não em graus. Assim, o ângulo 0 representa a posição 3 horas no relógio. A posição de 9 horas é (1 * PI), 12 horas é (1.5 * PI) e 6 horas é (0.5 * PI). Portanto, se você quiser desenhar um círculo completo, deverá sair do ângulo 0 e ir até (2 * PI).

Veja um trecho de código que desenha um arco equivalente a um quarto de uma pizza, ou seja, 25%, saindo do ângulo 90º (em graus) e indo até 180º (graus):

<html>
<head>
  <meta charset="utf-8">
  <title>Estudos HTML5</title>
</head>
<body>

<Canvas id="canvas1" width="500" height="350"></Canvas>
 
<script type="text/javascript">
  // obtemos uma referência ao elemento Canvas  
  var canvas = document.getElementById("canvas1");
  // obtemos o contexto de desenho
  var contexto = canvas.getContext("2d");
     
  // vamos desenhar um arco sem preenchimento com raio de 80
  contexto.beginPath(); // início um novo caminho
  // o arco começa no x = 100, y = 100, começa no ângulo 90 (em graus)
  // e vai até o ânculo 180 (graus)
  // as medidas na função arc() são em radianos, não em graus
  contexto.arc(100, 100, 80, Math.PI, 1.5 * Math.PI, false);
  contexto.lineWidth = 2; // largura da linha
  contexto.strokeStyle = '#990000'; // cor da linha
 
  contexto.stroke(); // realiza o desenho    
</script>

</body>
</html>

Execute este código e veja que o arco realmente foi desenhado. Seu resultado deverá ser parecido com: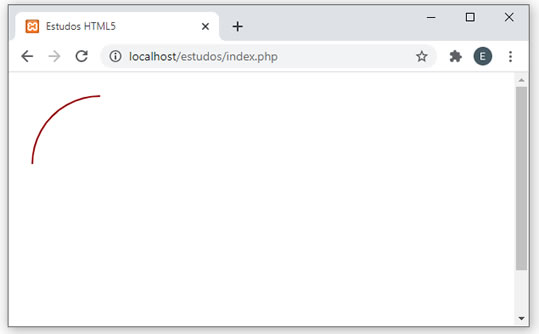



No entanto, para parecer um pedação de pizza, ou seja, o ponto de partida para um gráfico de pizza, é preciso que tenhamos duas linhas ligado esse arco ao centro do círculo. Veja a modificação que fiz:

<html>
<head>
  <meta charset="utf-8">
  <title>Estudos HTML5</title>
</head>
<body>

<Canvas id="canvas1" width="500" height="350"></Canvas>
 
<script type="text/javascript">
  // obtemos uma referência ao elemento Canvas  
  var canvas = document.getElementById("canvas1");
  // obtemos o contexto de desenho
  var contexto = canvas.getContext("2d");
     
  // vamos desenhar um arco sem preenchimento com raio de 80
  contexto.beginPath(); // início um novo caminho
   
  // primeiro movemos a caneta de desenho para o centro do círculo
  contexto.moveTo(100, 100);
 
  // o arco começa no x = 100, y = 100, começa no ângulo 90 (em graus)
  // e vai até o ânculo 180 (graus)
  // as medidas na função arc() são em radianos, não em graus
  contexto.arc(100, 100, 80, Math.PI, 1.5 * Math.PI, false);
  contexto.lineWidth = 2; // largura da linha
  contexto.strokeStyle = '#990000'; // cor da linha
 
  // agora desenhamos uma linha de volta para o arco
  contexto.lineTo(100, 100);
 
  contexto.stroke(); // realiza o desenho    
</script>

</body>
</html>

Execute novamente e veja que agora o efeito ficou bem melhor. Seu resultado deverá ser parecido com: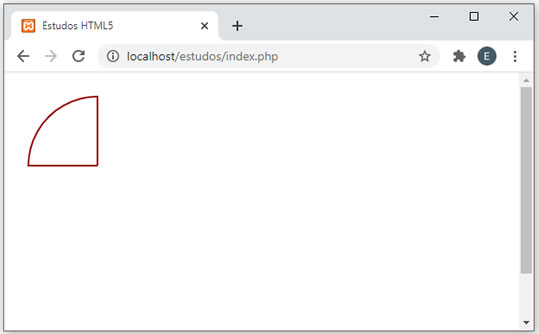



Para finalizar, vamos colorir o pedação de pizza. Veja a nova versão (com o código completo):

<!doctype html>
<html>
<head>
  <title>O objeto Canvas do HTML5</title>
</head>
 
<body>
 
<Canvas id="canvas1" width="500" height="350"></Canvas>
 
<script type="text/javascript">
  // obtemos uma referência ao elemento Canvas  
  var canvas = document.getElementById("canvas1");
  // obtemos o contexto de desenho
  var contexto = canvas.getContext("2d");
     
  // vamos desenhar um arco sem preenchimento com raio de 80
  contexto.beginPath(); // início um novo caminho
   
  // primeiro movemos a caneta de desenho para o centro do círculo
  contexto.moveTo(100, 100);
 
  // o arco começa no x = 100, y = 100, começa no ângulo 90 (em graus)
  // e vai até o ânculo 180 (graus)
  // as medidas na função arc() são em radianos, não em graus
  contexto.arc(100, 100, 80, Math.PI, 1.5 * Math.PI, false);
  contexto.lineWidth = 2; // largura da linha
  contexto.strokeStyle = '#990000'; // cor da linha
 
  // agora desenhamos uma linha de volta para o arco
  contexto.lineTo(100, 100);
 
  // vamos preencher o gráfico
  contexto.fillStyle = "#CCCCCC"; // cor do preenchimento
  contexto.fill(); // preenche de fato
 
  contexto.stroke(); // realiza o desenho    
</script>
 
</body>
</html>

Agora o resultado será: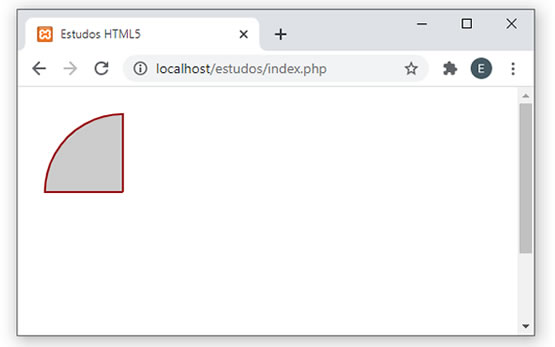



LISP ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas

Como calcular o cosseno de um ângulo em LISP e AutoLISP (AutoCAD) usando a função cos() - Calculadora de cosseno em LISP

Quantidade de visualizações: 871 vezes
Em geral, quando falamos de cosseno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função cosseno disponível nas linguagens de programação para calcular o cosseno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria.

No entanto, é sempre importante entender o que é a função cosseno. Veja a seguinte imagem:



Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles.

Assim, o cosseno é a razão entre o cateto adjascente e a hipotenusa, ou seja, o cateto adjascente dividido pela hipotenusa. Veja a fórmula:

\[\text{Cosseno} = \frac{\text{Cateto adjascente}}{\text{Hipotenusa}} \]

Então, se dividirmos 30 por 36.056 (na figura eu arredondei) nós teremos 0.8320, que é a razão entre o cateto adjascente e a hipotenusa (em radianos).

Agora, experimente calcular o arco-cosseno de 0.8320. O resultado será 0.5881 (em radianos). Convertendo 0.5881 radianos para graus, nós obtemos 33.69º, que é exatamente o ângulo em graus entre o cateto adjascente e a hipotenusa na figura acima.

Pronto! Agora que já sabemos o que é cosseno na trigonometria, vamos entender mais sobre a função cos() da Common Lisp e da AutoLISP (a implementação LISP do AutoCAD). Esta função recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja:

(format t "Cosseno de 0 = ~F~%" (cos 0))
(format t "Cosseno de 1 = ~F~%" (cos 1))
(format t "Cosseno de 2 = ~F" (cos 2))

Ao executar este código LISP nós teremos o seguinte resultado:

Cosseno de 0 = 1.0
Cosseno de 1 = 0.5403023
Cosseno de 2 = -0.41614684

Note que calculamos os cossenos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função cosseno mostrada abaixo: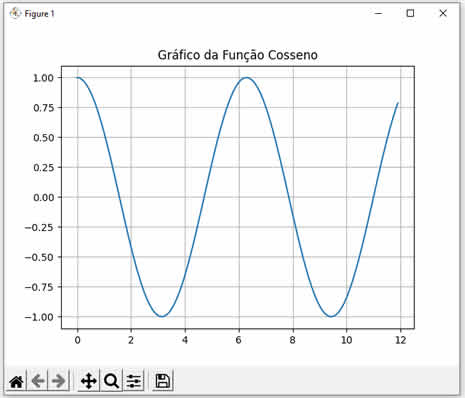



PHP ::: Dicas & Truques ::: Geometria, Trigonometria e Figuras Geométricas

Como calcular o coeficiente angular de uma reta em PHP dados dois pontos no plano cartesiano

Quantidade de visualizações: 1351 vezes
O Coeficiente Angular de uma reta é a variação, na vertical, ou seja, no eixo y, pela variação horizontal, no eixo x. Sim, isso mesmo. O coeficiente angular de uma reta tem tudo a ver com a derivada, que nada mais é que a taxa de variação de y em relação a x.

Vamos começar analisando o seguinte gráfico, no qual temos dois pontos distintos no plano cartesiano:



Veja que o segmento de reta AB passa pelos pontos A (x=3, y=6) e B (x=9, y=10). Dessa forma, a fórmula para obtenção do coeficiente angular m dessa reta é:

\[\ \text{m} = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} = tg \theta \]

Note que __$\Delta y__$ e __$\Delta x__$ são as variações dos valores no eixo das abscissas e no eixo das ordenadas. No triângulo retângulo que desenhei acima, a variação __$\Delta y__$ se refere ao comprimento do cateto oposto e a variação __$\Delta y__$ se refere ao comprimento do cateto adjascente.

Veja agora o trecho de código na linguagem PHP que solicita as coordenadas x e y dos dois pontos, efetua o cálculo e mostra o coeficiente angular m da reta que passa pelos dois pontos:

<?php
  // x e y do primeiro ponto
  $x1 = 3;
  $y1 = 6;
    
  // x e y do segundo ponto
  $x2 = 9;
  $y2 = 10;   
     
  $m = ($y2 - $y1) / ($x2 - $x1);
     
  // mostramos o resultado
  echo "O coeficiente angular é: " . $m;
?>

Ao executar este código PHP nós teremos o seguinte resultado:

O coeficiente angular é: 0.66666666666667

Veja agora como podemos calcular o coeficiente angular da reta que passa pelos dois pontos usando o Teorema de Pitágoras. Note que agora nós estamos tirando proveito da tangente do ângulo Theta (__$\theta__$), também chamado de ângulo Alfa ou Alpha (__$\alpha__$):

<?php
  // x e y do primeiro ponto
  $x1 = 3;
  $y1 = 6;
    
  // x e y do segundo ponto
  $x2 = 9;
  $y2 = 10;   
     
  // vamos obter o comprimento do cateto oposto
  $cateto_oposto = $y2 - $y1;
  // e agora o cateto adjascente
  $cateto_adjascente = $x2 - $x1;
  // vamos obter o ângulo tetha, ou seja, a inclinação da hipetunesa
  // (em radianos, não se esqueça)
  $tetha = atan2($cateto_oposto, $cateto_adjascente);
  // e finalmente usamos a tangente desse ângulo para calcular
  // o coeficiente angular
  $tangente = tan($tetha);
     
  // mostramos o resultado
  echo "O coeficiente angular é: " . $tangente;
?>

Ao executar este código você verá que o resultado é o mesmo. No entanto, fique atento às propriedades do coeficiente angular da reta:

1) O coeficiente angular é positivo quando a reta for crescente, ou seja, m > 0;

2) O coeficiente angular é negativo quando a reta for decrescente, ou seja, m < 0;

3) Se a reta estiver na horizontal, ou seja, paralela ao eixo x, seu coeficiente angular é zero (0).

4) Se a reta estiver na vertical, ou seja, paralela ao eixo y, o coeficiente angular não existe.

Carregar Publicações Anteriores

Nossas 20 dicas & truques de programação mais populares

Você também poderá gostar das dicas e truques de programação abaixo

Nossas 20 dicas & truques de programação mais recentes

Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site

Últimos Exercícios Resolvidos

E-Books em PDF
E-Book 350 Exercícios Resolvidos de Java - PDF com 500 páginas
Domine lógica de programação e a linguagem Java com o nosso E-Book 350 Exercícios Exercícios de Java, para você estudar onde e quando quiser.

Este e-book contém exercícios resolvidos abrangendo os tópicos: Java básico, matemática e estatística, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.
Ver Conteúdo do E-book
E-Book 650 Dicas, Truques e Exercícios Resolvidos de Python - PDF com 1.200 páginas
Domine lógica de programação e a linguagem Python com o nosso E-Book 650 Dicas, Truques e Exercícios Exercícios de Python, para você estudar onde e quando quiser.

Este e-book contém dicas, truques e exercícios resolvidos abrangendo os tópicos: Python básico, matemática e estatística, banco de dados, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.
Ver Conteúdo do E-book

Linguagens Mais Populares

1º lugar: Java
2º lugar: Python
3º lugar: C#
4º lugar: PHP
5º lugar: C
6º lugar: Delphi
7º lugar: JavaScript
8º lugar: C++
9º lugar: VB.NET
10º lugar: Ruby
E-Book 350 Exercícios Resolvidos de Java - PDF com 500 páginas
Domine lógica de programação e a linguagem Java com o nosso E-Book 350 Exercícios Exercícios de Java, para você estudar onde e quando quiser. Este e-book contém exercícios resolvidos abrangendo os tópicos: Java básico, matemática e estatística, programação dinâmica, strings e caracteres, entrada e saída, estruturas condicionais, vetores e matrizes, funções, laços, recursividade, internet, arquivos e diretórios, programação orientada a objetos e muito mais.
Ver Conteúdo do E-book Apenas R$ 19,90
Questões de Concurso para Engenharia Civil
Fundações
Instalações Hidráulicas Prediais
Fenômenos de Transporte e Hidráulica
Estruturas de Aço e Madeira
Exercícios Resolvidos
Lista de Exercícios Resolvidos de Java
Lista de Exercícios Resolvidos de C
Lista de Exercícios Resolvidos de C++
Bancos de Dados
MySQL
Firebird
MS SQL Server
PostgreSQL
Questões de Concurso
Topografia
Hidrologia
Hidrostática
Ética e Legislação Profissional
Frameworks
jQuery
AngularJS
React / ReactJS / React.js
Laravel
Projetos e Códigos Fonte
Projetos e Códigos Fonte Java
Projetos e Códigos Fonte PHP
Projetos e Códigos Fonte Python
Especializações
Data Science
Calculadoras
Calculadoras de Topografia
Calculadoras de Matemática
Calculadoras de Data e Hora
Calculadoras de Física
Calculadoras de Estatística
Calculadoras de Trigonometria
Calculadoras de Matrizes
Calculadoras de Vetores
Ferramentas
Tabela de Cores Flat Design
Tabela de Cores do Material Design do Google
Tabela de Cores Web Safe Colors
Todas as Linguagens, Frameworks, Biliotecas e Bancos de Dados
.NET Framework | ActionScript | Adobe AIR | Adobe Flex | AJAX | Android Java | Angular | AngularJS | Apache Ant | Apache Maven | Apache Tomcat | Apache Web Server | Arduino | ASP.NET | AutoCAD | AutoCAD .NET API C# | AutoCAD Civil 3D | AutoCAD Civil 3D .NET C# | AutoCAD VBA | AutoLISP | Bourne Again Shell (bash Shell) | C | C# | C++ | C++ Builder | CodeIgniter | CSS | Dart | Data Science | Delphi | DHTML (Dynamic HTML) | Django | Eclipse IDE | Elixir | Enterprise JavaBeans (EJB) | Erlang | Excel | Excel VBA | Ext JS | Facelets | Firebird | Flutter | Fórmulas da Física | Geral | GNU Octave | GoLang | Groovy | GTK+ | Haskell | HEC-RAS | Hibernate | HTML/XHTML | HTML5 | IBM DB2 | iReport | iTextSharp | Java | Java Servlets | JavaFX | JavaScript | JBoss | JPA - Java Persistence Architecture API - Arquitetura de Persistência Java | jQuery | jQuery UI | JSF - Java Server Faces | JSP (Java Server Pages) | Kotlin | Laravel | Linux | LISP | MongoDB | MS SQL Server | MySQL | NetBeans IDE | NetBeans IDE | Node.js | Perl | PHP | PHP-GTK | Portugol | PostgreSQL | Processing.py | Python | QGIS | Qt | R | React | React Native | React.js | Revit C# | Revit Python Shell | Ruby | Ruby On Rails | Rust | Smarty | Struts | Struts 2 | Tcl e Tcl/Tk | TypeScript | VB.NET | VBA | Visual LISP | VisuAlg | WebGL (Web Graphics Library) | wxWidgets | Zend Framework |

© 2025 Arquivo de Códigos - Todos os direitos reservados
Neste momento há 70 usuários muito felizes estudando em nosso site.