 |
|||||
 Planilha Web - Planilhas e Calculadoras online para estudantes e profissionais de Engenharia Civil, Engenharia Elétrica e Engenharia Mecânica. |
|||||
|
|||||
GNU Octave ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o seno de um número ou ângulo em GNU Octave usando a função sin()Quantidade de visualizações: 2325 vezes |
|
Em geral, quando falamos de seno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função seno disponível nas linguagens de programação para calcular o seno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função seno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o seno é a razão entre o cateto oposto (oposto ao ângulo theta) e a hipotenusa, ou seja, o cateto oposto dividido pela hipotenusa. Veja a fórmula: \[\text{Seno} = \frac{\text{Cateto oposto}}{\text{Hipotenusa}} \] Então, se dividirmos 20 por 36.056 (na figura eu arredondei) nós teremos 0.5547, que é a razão entre o cateto oposto e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.5547. O resultado será 0.9828 (em radianos). Convertendo 0.9828 radianos para graus, nós obtemos 56.31º, que é exatamente o ângulo em graus entre o cateto oposto e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é seno na trigonometria, vamos entender mais sobre a função sin() da linguagem GNU Octave. Esta função, que já vem embutido na ferramenta, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja: >> sin(0) [ENTER] ans = 0 >> sin(1) [ENTER] ans = 0.8415 >> sin(2) [ENTER] ans = 0.9093 >> Note que calculamos os senos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função seno mostrada abaixo: 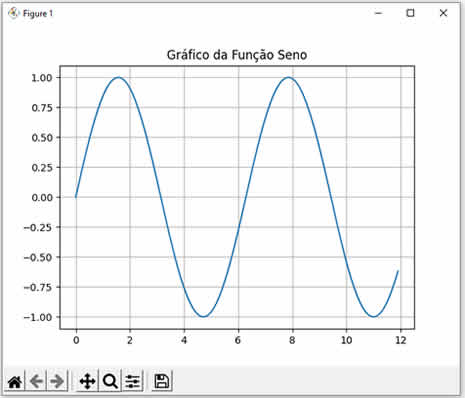 |
PHP ::: Dicas & Truques ::: Variáveis e Constantes |
Como verificar se uma variável PHP é do tipo object usando a função is_object()Quantidade de visualizações: 9374 vezes |
|
Em algumas situações podemos querer saber se o tipo de uma determinada variável é object. Este teste pode ser feito com o auxílio da função is_object() da linguagem PHP. Esta função retorna um valor true se a variável for do tipo object e false em caso contrário. Veja o código completo para o exemplo:
<html>
<head>
<title>Estudos PHP</title>
</head>
<body>
<?php
class Pessoa{
public $nome = '';
function nome($novo_nome = NULL){
if(!is_null($novo_nome)){
$this->nome = $novo_nome;
}
return $this->nome;
}
}
$pessoa = new Pessoa;
if(is_object($pessoa)){
echo 'A variável $pessoa é do tipo object.';
}
?>
</body>
</html>
Ao executarmos este código PHP nós teremos o seguinte resultado: A variável $pessoa é do tipo object. |
Python ::: Dicas & Truques ::: Matemática e Estatística |
Apostila Python para iniciantes - Como calcular juros compostos e montante usando PythonQuantidade de visualizações: 18072 vezes |
|
O regime de juros compostos é o mais comum no sistema financeiro e portanto, o mais útil para cálculos de problemas do dia-a-dia. Os juros gerados a cada período são incorporados ao principal para o cálculo dos juros do período seguinte. Chamamos de capitalização o momento em que os juros são incorporados ao principal. Após três meses de capitalização, temos: 1º mês: M = P . (1 + i) 2º mês: o principal é igual ao montante do mês anterior: M = P x (1 + i) x (1 + i) 3º mês: o principal é igual ao montante do mês anterior: M = P x (1 + i) x (1 + i) x (1 + i) Simplificando, obtemos a fórmula: M = P . (1 + i) ^ n Importante: a taxa i tem que ser expressa na mesma medida de tempo de n, ou seja, taxa de juros ao mês para n meses. Para calcularmos apenas os juros basta diminuir o principal do montante ao final do período: J = M - P Vejamos um exemplo: Considerando que uma pessoa empresta a outra a quantia de R$ 2.000,00, a juros compostos, pelo prazo de 3 meses, à taxa de 3% ao mês. Quanto deverá ser pago de juros? Veja o código Python para a resolução:
# função principal do programa
def main():
principal = 2000.00
taxa = 0.03
meses = 3
montante = principal * pow((1 + taxa), meses)
juros = montante - principal
print("O total de juros a ser pago é:", juros)
print("O montante a ser pago é:", montante)
if __name__== "__main__":
main()
Ao executarmos este código Python nós teremos o seguinte resultado: O total de juros a ser pago é: 185.45400000000018 O montante a ser pago é: 2185.454 Um outra aplicação interessante é mostrar mês a mês a evolução dos juros. Veja o código a seguir:
# função principal do programa
def main():
principal = 2000.00
taxa = 0.03
meses = 3
anterior = 0.0
for i in range(1, meses + 1):
montante = principal * pow((1 + taxa), i)
juros = montante - principal - anterior
anterior += juros
print("Mês:", i ," - Montante:", montante, "- Juros:", juros)
if __name__== "__main__":
main()
Ao executarmos este código Python nós teremos o seguinte resultado: Mês: 1 - Montante: 2060.0 - Juros: 60.0 Mês: 2 - Montante: 2121.7999999999997 - Juros: 61.79999999999973 Mês: 3 - Montante: 2185.454 - Juros: 63.65400000000045 |
JavaScript ::: Dicas & Truques ::: Matemática e Estatística |
Como resolver uma equação do segundo grau em JavaScript - Como calcular Bhaskara em JavaScriptQuantidade de visualizações: 967 vezes |
|
Como resolver uma equação do 2º grau usando JavaScript Nesta dica mostrarei como encontrar as raízes de uma equação quadrática, ou seja, uma equação do 2º usando a linguagem JavaScript. Definimos como equação do 2º grau ou equações quadráticas qualquer equação do tipo ax² + bx + c = 0 em que a, b e c são números reais e a ≠ 0. Ela recebe esse nome porque, no primeiro membro da igualdade, há um polinômio de grau dois com uma única incógnita. Note que, dos coeficientes a, b e c, somente o a é diferente de zero, pois, caso ele fosse igual a zero, o termo ax² seria igual a zero, logo a equação se tornaria uma equação do primeiro grau: bx + c = 0. Independentemente da ordem da equação, o coeficiente a sempre acompanha o termo x², o coeficiente b sempre acompanha o termo x, e o coeficiente c é sempre o termo independente. Como resolver uma equação do 2º grau Conhecemos como soluções ou raízes da equação ax² + bx + c = 0 os valores de x que fazem com que essa equação seja verdadeira. Uma equação do 2º grau pode ter no máximo dois números reais que sejam raízes dela. Para resolver equações do 2º grau completas, existem dois métodos mais comuns: a) Fórmula de Bhaskara; b) Soma e produto. O primeiro método é bastante mecânico, o que faz com que muitos o prefiram. Já para utilizar o segundo, é necessário o conhecimento de múltiplos e divisores. Além disso, quando as soluções da equação são números quebrados, soma e produto não é uma alternativa boa. Como resolver uma equação do 2º grau usando Bhaskara Como nosso código JavaScript vai resolver a equação quadrática usando a Fórmula de Bhaskara, o primeiro passo é encontrar o determinante. Veja: \[\Delta =b^2-4ac\] Nem sempre a equação possui solução real. O valor do determinante é que nos indica isso, existindo três possibilidades: a) Se determinante > 0, então a equação possui duas soluções reais. b) Se determinante = 0, então a equação possui uma única solução real. c) Se determinante < 0, então a equação não possui solução real. Encontrado o determinante, só precisamos substituir os valores, incluindo o determinante, na Fórmula de Bhaskara: \[x = \dfrac{- b\pm\sqrt{b^2- 4ac}}{2a}\] Vamos agora ao código JavaScript. Nossa aplicação vai pedir para o usuário informar os valores dos três coeficientes a, b e c e, em seguida, vai apresentar as raizes da equação:
<!doctype html>
<html>
<head>
<title>Aprenda Matemática Usando JavaScript</title>
</head>
<body>
<script type="text/javascript">
// os coeficientes
var a, b, c;
// as duas raizes, a imaginaria e o discriminante
var raiz1, raiz2, imaginaria, discriminante;
// vamos pedir para o usuário informar os valores dos coeficientes
a = parseFloat(window.prompt("Valor do coeficiente a: "));
b = parseFloat(window.prompt("Valor do coeficiente b: "));
c = parseFloat(window.prompt("Valor do coeficiente c: "));
// vamos calcular o discriminante
discriminante = (b * b) - (4 * a * c);
// a equação possui duas soluções reais?
if(discriminante > 0){
raiz1 = (-b + Math.sqrt(discriminante)) / (2 * a);
raiz2 = (-b - Math.sqrt(discriminante)) / (2 * a);
document.write("Existem duas raizes: x1 = " + raiz1
+ " e x2 = " + raiz2);
}
// a equação possui uma única solução real?
else if(discriminante == 0){
raiz1 = raiz2 = -b / (2 * a);
document.write("Existem duas raizes iguais: x1 = "
+ raiz1 + " e x2 = " + raiz2);
}
// a equação não possui solução real?
else if(discriminante < 0){
raiz1 = raiz2 = -b / (2 * a);
imaginaria = Math.sqrt(-discriminante) / (2 * a);
document.write("Existem duas raízes complexas: x1 = " +
raiz1 + " + " + imaginaria + " e x2 = " + raiz2
+ " - " + imaginaria);
}
</script>
</body>
</html>
Ao executar este código JavaScript nós teremos o seguinte resultado: Valor do coeficiente a: 1 Valor do coeficiente b: 2 Valor do coeficiente c: -3 Existem duas raizes: x1 = 1 e x2 = -3 |
JavaScript ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como testar se ao menos um elemento de um array satisfaz uma condição em JavaScript usando a função some()Quantidade de visualizações: 2203 vezes |
|
O método some(), adicionado à linguagem JavaScript por meio do ECMAScript 5 (JavaScript 5, ECMAScript 2009, ES5) pode ser usado quando queremos verificar se um ou mais elementos de um vetor satisfaz uma determinada condição. Este método nos permite fornecer uma função de callback que será chamada para cada um dos elementos do vetor. E o retorno do método some() é um valor true se ao menos um dos elementos passar no teste e false em caso contrário. Tão logo o valor true seja satisfeito, a função some() encerra sua execução imediatamente. Veja um exemplo no qual testamos se AO MENOS um elemento do array é maior que 70:
<script type="text/javascript">
function testar(valor, indice, vetor){
if(valor > 70){
return true;
}
}
var valores = new Array(21, 50, 30, 71, 12, 3);
// vamos verificar se AO MENOS um valor é maior que 70
var res = valores.some(testar);
window.alert("Alguns valores passaram no teste: " + res);
</script>
Aqui o resultado será true, pois o valor 71 passou no teste. É importante observar que, assim que a função de callback retorna true pela primeira vez, o método some() já abandona sua execução. Uma função passada para o método some() pode conter os seguintes argumentos (nessa mesma ordem): a) O valor do item; b) O índice do item (opcional); c) O vetor a partir do qual o método some() está sendo chamado (opcional). Como última observação, o método some() não modifica o array original. |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Exercícios Resolvidos de Java - Como inverter a ordem dos elementos de um array usando apenas uma variável temporáriaQuantidade de visualizações: 9668 vezes |
|
Pergunta/Tarefa: Considere o seguinte trecho de código:
// declara, constrói e inicializa um array de 10 inteiros
int valores[] = {6, 3, 90, 1, 54, 7, 12, 32, 9, 4};
int temp;
Ordem inicial: 6 3 90 1 54 7 12 32 9 4 Ordem invertida: 4 9 32 12 7 54 1 90 3 6 Veja a resolução comentada deste exercício usando Java console:
package estudos;
public class Estudos {
public static void main(String[] args) {
// declara, constrói e inicializa um array de 10 inteiros
int valores[] = {6, 3, 90, 1, 54, 7, 12, 32, 9, 4};
int temp;
// vamos mostar a ordem inicial dos elementos no vetor
System.out.print("Ordem inicial: ");
for(int i = 0; i < valores.length; i++){
System.out.print(valores[i] + " ");
}
// vamos inverter a ordem dos elementos no array
int inicio = 0, fim = valores.length - 1;
while(inicio < fim){
temp = valores[inicio];
valores[inicio] = valores[fim];
valores[fim] = temp;
// incrementa e decrementa as variáveis de controle
inicio++;
fim--;
}
// vamos mostar a ordem invertida dos elementos do vetor
System.out.print("\nOrdem invertida: ");
for(int i = 0; i < valores.length; i++){
System.out.print(valores[i] + " ");
}
System.out.println();
}
}
|
Portugol ::: Dicas & Truques ::: Cadeias e Caracteres |
Como remover todos os espaços de um nome, frase ou texto usando a função substituir() da biblioteca Texto do PortugolQuantidade de visualizações: 217 vezes |
|
Como remover espaços de um nome, frase ou texto usando a função substituir() da biblioteca Texto do Portugol Nesta dica mostrarei como podemos usar a função substituir() da biblioteca Texto do Portugol para remover todas as ocorrências de espaços em um nome, frase ou texto. Esta técnica é muito interessante quando queremos processar e salvar dados informados pelos usuários em um arquivo texto. Veja o código Portugol completo para o exemplo:
programa {
// vamos incluir a biblioteca Texto
inclua biblioteca Texto --> texto
funcao inicio() {
// vamos declarar uma variável para guardar um nome
cadeia nome, novo_nome
// vamos pedir para o usuário informar o seu nome
escreva("Informe o seu nome: ")
leia(nome)
// agora vamos remover todos os espaços do nome informado
novo_nome = texto.substituir(nome, " ", "")
// e mostramos os resultados
escreva("Você informou o nome: " + nome)
escreva("\nSem os espaços: " + novo_nome)
}
}
Ao executar este código Portugol nós teremos o seguinte resultado: Informe o seu nome: Marcela de Oliveira Macedo Cunha Você informou o nome: Marcela de Oliveira Macedo Cunha Sem os espaços: MarceladeOliveiraMacedoCunha |
Python ::: Dicas & Truques ::: Matemática e Estatística |
Como resolver uma equação do segundo grau em Python - Como calcular Bhaskara em PythonQuantidade de visualizações: 2622 vezes |
|
Como resolver uma equação do 2º grau usando Python Nesta dica mostrarei como encontrar as raízes de uma equação quadrática, ou seja, uma equação do 2º usando a linguagem Python. Definimos como equação do 2º grau ou equações quadráticas qualquer equação do tipo ax² + bx + c = 0 em que a, b e c são números reais e a ≠ 0. Ela recebe esse nome porque, no primeiro membro da igualdade, há um polinômio de grau dois com uma única incógnita. Note que, dos coeficientes a, b e c, somente o a é diferente de zero, pois, caso ele fosse igual a zero, o termo ax² seria igual a zero, logo a equação se tornaria uma equação do primeiro grau: bx + c = 0. Independentemente da ordem da equação, o coeficiente a sempre acompanha o termo x², o coeficiente b sempre acompanha o termo x, e o coeficiente c é sempre o termo independente. Como resolver uma equação do 2º grau Conhecemos como soluções ou raízes da equação ax² + bx + c = 0 os valores de x que fazem com que essa equação seja verdadeira. Uma equação do 2º grau pode ter no máximo dois números reais que sejam raízes dela. Para resolver equações do 2º grau completas, existem dois métodos mais comuns: a) Fórmula de Bhaskara; b) Soma e produto. O primeiro método é bastante mecânico, o que faz com que muitos o prefiram. Já para utilizar o segundo, é necessário o conhecimento de múltiplos e divisores. Além disso, quando as soluções da equação são números quebrados, soma e produto não é uma alternativa boa. Como resolver uma equação do 2º grau usando Bhaskara Como nosso código Python vai resolver a equação quadrática usando a Fórmula de Bhaskara, o primeiro passo é encontrar o determinante. Veja: \[\Delta =b^2-4ac\] Nem sempre a equação possui solução real. O valor do determinante é que nos indica isso, existindo três possibilidades: a) Se determinante > 0, então a equação possui duas soluções reais. b) Se determinante = 0, então a equação possui uma única solução real. c) Se determinante < 0, então a equação não possui solução real. Encontrado o determinante, só precisamos substituir os valores, incluindo o determinante, na Fórmula de Bhaskara: \[x = \dfrac{- b\pm\sqrt{b^2- 4ac}}{2a}\] Vamos agora ao código Python. Nossa aplicação vai pedir para o usuário informar os valores dos três coeficientes a, b e c e, em seguida, vai apresentar as raizes da equação:
# importamos a bibliteca Math
import math
def main():
# vamos pedir para o usuário informar os valores dos coeficientes
a = float(input("Valor do coeficiente a: "))
b = float(input("Valor do coeficiente b: "))
c = float(input("Valor do coeficiente c: "))
# vamos calcular o discriminante
discriminante = (b * b) - (4 * a * c)
# a equação possui duas soluções reais?
if(discriminante > 0):
raiz1 = (-b + math.sqrt(discriminante)) / (2 * a)
raiz2 = (-b - math.sqrt(discriminante)) / (2 * a)
print("Existem duas raizes: x1 = {0} e x2 = {1}".format(raiz1, raiz2))
# a equação possui uma única solução real?
elif(discriminante == 0):
raiz1 = raiz2 = -b / (2 * a)
print("Existem duas raizes iguais: x1 = {0} e x2 = {1}".format(raiz1, raiz2))
# a equação não possui solução real?
elif(discriminante < 0):
raiz1 = raiz2 = -b / (2 * a)
imaginaria = math.sqrt(-discriminante) / (2 * a)
print("Existem duas raízes complexas: x1 = {0} + {1} e x2 = {2} - {3}".format(
raiz1, imaginaria, raiz2, imaginaria))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Valor do coeficiente a: 1 Valor do coeficiente b: 2 Valor do coeficiente c: -3 Existem duas raizes: x1 = 1.0 e x2 = -3.0 |
Delphi ::: Dicas & Truques ::: MIDI Musical Instrument Digital Interface, Mapeamento e sequenciamento MIDI, Entrada e saída MIDI |
Como abrir e fechar um dispositivo de saída MIDI usando DelphiQuantidade de visualizações: 11457 vezes |
Quando queremos executar sons MIDI no Windows, a primeira tarefa a ser realizada é abrir o dispositivo de saída MIDI. Isso é feito com uma chamada à função midiOutOpen() da API do Windows. Veja sua assinatura (em C):MMRESULT midiOutOpen( LPHMIDIOUT lphmo, UINT_PTR uDeviceID, DWORD_PTR dwCallback, DWORD_PTR dwCallbackInstance, DWORD dwFlags ); Esta função está traduzida na unit MMSystem.pas do Delphi da seguinte forma: function midiOutOpen(lphMidiOut: PHMIDIOUT; uDeviceID: UINT; dwCallback, dwInstance, dwFlags: DWORD): MMRESULT; stdcall; Antes de continuarmos, vamos entender os parâmetros desta função: lphmo - Este é um ponteiro para um HMIDIOUT (que é simplemente um Integer). Este ponteiro é preenchido com um handle identificando o dispositivo de saída MIDI aberto. Este handle é usado para identificar o dispositivo nas demais chamadas de saída MIDI. uDeviceID - Identificador do dispositivo de saída MIDI a ser aberto. O valor 0 aqui é seguro, visto que este identifica o primeiro dispositivo na lista de dispositivos de saída. Veja minha dica "Como obter uma lista dos dispositivos de saída MIDI no sistema" para mais informações. dwCallback - Um ponteiro para uma função de callback, um handle de evento, um identificador de thread ou um handle para uma janela ou thread chamada durante o playback do MIDI para processar mensagens relacionadas ao processo de playback. Se não houver nada a ser processado, podemos definir o valor 0 para este parâmetro. Dê uma olhada na minha dica relacionada à função MidiOutProc(). dwCallbackInstance - Dados de instância do usuário passados para a função de callback. Este parâmetro não é usado em callbacks de janela e thread. É seguro manter seu valor como 0. dwFlags - Flag de callback para abrir o dispositivo. Por enquanto vamos manter seu valor como CALLBACK_NULL. Veja minhas outras dicas sobre o assunto para aprofundar mais neste parâmetro. Agora que aprendemos mais sobre os parâmetros da função midiOutOpen(), vamos ver como usá-la para abrir um dispositivo de saída MIDI e tocar a nota DÓ média (aquela no meio da escala de notas possíveis). Veja o código completo para a unit:
unit Unit2;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, MMSystem;
type
TForm2 = class(TForm)
Button1: TButton;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
dispositivo: HMIDIOUT; // dispositivo de saída MIDI
public
{ Public declarations }
end;
var
Form2: TForm2;
implementation
{$R *.dfm}
procedure TForm2.Button1Click(Sender: TObject);
var
erro: Word;
begin
erro := midiOutOpen(@dispositivo, 0, 0, 0, CALLBACK_NULL);
// houve erro na abertura do dispositivo de saída MIDI?
if (erro <> 0) then
begin
ShowMessage('Não foi possível abrir o dispositivo MIDI. Erro: ' + IntToStr(erro));
end
else
begin
ShowMessage('Dispositivo MIDI aberto com sucesso.');
// vamos tocar uma nota para nos certificarmos de que o dispositivo
// realmente foi aberto e está funcionando
// vamos tocar a nota DÓ média e com velocidade máxima
midiOutShortMsg(dispositivo, rgb($90, 60, 127));
// vamos deixar a nota soar um pouco
sleep(1000);
// vamos silenciar a nota
midiOutShortMsg(dispositivo, rgb($80, 60, 0));
// finalmente vamos fechar o dispositivo MIDI
midiOutClose(dispositivo);
end;
end;
end.
O primeiro passo foi declarar uma variável do tipo HMIDIOUT: dispositivo: HMIDIOUT; Este é o dispositivo de saída que será usado nas demais chamadas MIDI, incluindo a função midiOutClose(), usada para fechar o dispositivo: midiOutClose(dispositivo); Na API do Windows está função está declarada da seguinte forma: MMRESULT midiOutClose( HMIDIOUT hmo ); Na unit MMSystem.pas do Delphi está função está traduzida da seguinte forma: function midiOutClose(hMidiOut: HMIDIOUT): MMRESULT; stdcall; Veja que só precisamos fornecer o nome da variável representando o dispositivo de saída MIDI aberto no momento para que a função se encarregue de fechá-lo. |
Firebird ::: Dicas & Truques ::: Tipos de Dados |
Como usar os tipos de dados DATE, TIME e TIMESTAMP do FirebirdQuantidade de visualizações: 30403 vezes |
|
No dialeto 3 (SQL DIALECT 3), o tipo de dados DATE do Firebird armazena apenas a data sozinha, ou seja, sem as horas. Esta forma de guardar apenas a data resulta em uma ocupação de 4 bytes (32 bits) na memória. A data armazenada pode variar de 01/01/0001 até 31/12/9999. No dialeto 1, (SQL DIALECT 1), o tipo DATE é o equivalente ao tipo TIMESTAMP do dialeto 3 (o tipo TIMESTAMP passou a existir somente a partir do dialeto 3). Veja um comando DDL CREATE TABLE que cria uma tabela do Firebird contendo um campo do tipo DATE: CREATE TABLE ALUNOS ( ID INTEGER NOT NULL, NOME VARCHAR(40) NOT NULL, NASCIMENTO DATE NOT NULL ); Aqui o campo ID é do tipo INTEGER, NOME é do tipo VARCHAR(40) e NASCIMENTO é do tipo DATE. Veja agora um comando DML INSERT INTO que insere um novo registro nesta tabela. Fique atento à forma como o valor da data é informado: INSERT INTO ALUNOS VALUES(1, 'OSMAR J. SILVA', '1981-11-28'); Veja que a data, assim como o valor para o campo NOME, foi informada entre aspas simples e seguindo o formato YYYY-MM-DD, ou seja, o ano, mês e dia separados por hifens. Para obter os dados inseridos pela query anterior, podemos usar o seguinte comando DML SELECT FROM: SELECT * FROM ALUNOS; Esta query resulta na exibição dos seguintes dados: ID NOME NASCIMENTO 1 OSMAR J. SILVA 28/11/1981 O tipo de dados TIME, disponível apenas a partir do dialeto 3 (SQL DIALECT 3) nos permite armazenar as horas, sem a data. Este tipo ocupa 4 bytes (32 bits) de memória e pode conter valores na faixa de 00:00 até 23:59:59.9999. Veja um comando DDL CREATE TABLE que cria uma tabela do Firebird contendo um campo do tipo TIME: CREATE TABLE COMPROMISSOS ( ID INTEGER NOT NULL, DESCRICAO VARCHAR(80) NOT NULL, DATA DATE NOT NULL, HORA TIME NOT NULL ); Veja que esta tabela possui 4 campos: ID do tipo INTEGER, DESCRICAO do tipo VARCHAR(80), DATA do tipo DATE e HORA do tipo TIME. Eis um comando DML INSERT INTO que mostra como inserir um registro nesta tabela: INSERT INTO COMPROMISSOS VALUES(10, 'ALMOÇO COM A ESPOSA', '2010-12-10', '19:00:00'); Note que, assim como fazemos com campos do tipo DATE, os valores para campos do tipo TIME também devem ser informados entre aspas simples. Veja um comando DML SELECT FROM que lista o registro inserido na query anterior: SELECT * FROM COMPROMISSOS; Esta query produz o seguinte resultado: ID DESCRICAO DATA HORA 10 ALMOÇO COM A ESPOSA 10/12/2010 19:00:00 O tipo TIMESTAMP, disponível apenas a partir do dialeto 3 (SQL DIALECT 3) nos permite armazenar a data e hora juntas. Este tipo ocupa 8 bytes (64 bits) de memória e é equivalente ao tipo DATE do dialeto 1. Veja um comando DDL CREATE TABLE que cria uma tabela do Firebird contendo um campo do tipo TIMESTAMP: CREATE TABLE COMPROMISSOS ( ID INTEGER NOT NULL, DESCRICAO VARCHAR(80) NOT NULL, DATA_HORA TIMESTAMP NOT NULL ); Veja que esta tabela possui três campos: ID é do tipo INTEGER, DESCRICAO é do tipo VARCHAR(80) e DATA_HORA é do tipo TIMESTAMP. Eis um comando DML INSERT INTO que mostra como inserir um registro nesta tabela: INSERT INTO COMPROMISSOS VALUES(20, 'ALMOÇO COM A ESPOSA', '2010-10-23 19:00:00'); Note que os valores para campos do tipo TIMESTAMP também devem ser informados entre aspas simples. Para finalizar, Veja um comando DML SELECT FROM que lista o registro inserido na query anterior: SELECT * FROM COMPROMISSOS; Esta query produz o seguinte resultado: ID DESCRICAO DATA_HORA 20 ALMOÇO COM A ESPOSA 23/10/2010 19:00:00 |
Nossas 20 dicas & truques de programação mais populares |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Python - Como retornar o dia do mês em Python como um decimal no intervalo 01-31 usando strftime("%d") JavaScript - Como retornar o tamanho de uma string em JavaScript usando a propriedade length do objeto String JavaScript - Como ordenar um array de strings em ordem alfabética em JavaScript - Vetores e matrizes em JavaScript Python - Python para iniciantes - Como inserir uma determinada quantidade de espaços à direita de uma string |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |




