Java ::: Desafios e Lista de Exercícios Resolvidos ::: Java Básico |
Exercícios Resolvidos de Java - Lendo a idade de um nadador e classificando sua categoria como infantil, juvenil, adolescente, adulto ou sêniorQuantidade de visualizações: 3855 vezes |
|
Pergunta/Tarefa: Escreva um programa Java que solicita a idade de um nadador e classifica sua categoria de acordo com as seguintes regras: a) De 5 a 7 anos - Infantil; b) De 8 a 10 anos - Juvenil; c) De 11 a 15 anos - Adolescente; d) De 16 a 30 anos - Adulto; e) Acima de 30 anos - Sênior. Sua saída deverá ser parecida com: Informe sua idade: 19 Sua categoria é Adulto Veja a resolução comentada deste exercício usando Java console:
package estudos;
import java.util.Scanner;
public class Exercicio {
public static void main(String[] args) {
Scanner entrada = new Scanner(System.in);
// vamos solicitar a idade do nadador
System.out.print("Informe sua idade: ");
int idade = Integer.parseInt(entrada.nextLine());
// vamos verificar a categoria do nadador
if((idade >= 5) && (idade <= 7)){
System.out.println("Sua categoria é Infantil");
}
else if((idade >= 8) && (idade <= 10)){
System.out.println("Sua categoria é Juvenil");
}
else if((idade >= 11) && (idade <= 15)){
System.out.println("Sua categoria é Adolescente");
}
else if((idade >= 16) && (idade <= 30)){
System.out.println("Sua categoria é Adulto");
}
else if(idade > 30){
System.out.println("Sua categoria é Sênior");
}
else{
System.out.println("Não pertence a nenhuma categoria.");
}
System.out.println("\n");
}
}
|
C# ::: C# para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como somar os elementos da diagonal principal de uma matriz em C#Quantidade de visualizações: 2722 vezes |
|
A Matriz quadrada é um tipo especial de matriz que possui o mesmo número de linhas e o mesmo número de colunas, ou seja, dada uma matriz Anxm, ela será uma matriz quadrada se, e somente se, n = m, onde n é o número de linhas e m é o número de colunas. Em geral as matrizes quadradas são chamadas de Matrizes de Ordem n, onde n é o número de linhas e colunas. Dessa forma, uma matriz de ordem 4 é uma matriz que possui 4 linhas e quatro colunas. Toda matriz quadrada possui duas diagonais, e elas são muito exploradas tanto na matemática quanto na construção de algorítmos. Essas duas diagonais são chamadas de Diagonal Principal e Diagonal Secundária. A diagonal principal de uma matriz quadrada une o seu canto superior esquerdo ao canto inferior direito. Veja: 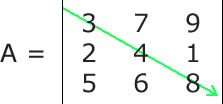 Nesta dica veremos como calcular a soma dos valores dos elementos da diagonal principal de uma matriz usando C#. Para isso, só precisamos manter em mente que a diagonal principal de uma matriz A é a coleção das entradas Aij em que i é igual a j. Assim, tudo que temos a fazer é converter essa regra para código C#. Veja um trecho de código C# completo no qual pedimos para o usuário informar os elementos da matriz e em seguida mostramos a soma dos elementos da diagonal superior:
using System;
namespace Estudos {
class Program {
static void Main(string[] args) {
// vamos declarar e construir uma matriz de três linhas
// e três colunas
int[,] matriz = new int[3, 3];
int soma_diagonal = 0; // guarda a soma dos elementos na diagonal
// principal
// vamos ler os valores para os elementos da matriz
for (int i = 0; i < matriz.GetLength(0); i++) { // linhas
for (int j = 0; j < matriz.GetLength(1); j++) { // colunas
Console.Write("Informe o valor para a linha " + i + " e coluna "
+ j + ": ");
matriz[i, j] = Int32.Parse(Console.ReadLine());
}
}
// vamos mostrar a matriz da forma que ela
// foi informada
Console.WriteLine();
// percorre as linhas
for (int i = 0; i < matriz.GetLength(0); i++) {
// percorre as colunas
for (int j = 0; j < matriz.GetLength(1); j++) {
Console.Write(" " + matriz[i, j]);
}
// passa para a próxima linha da matriz
Console.WriteLine();
}
// vamos calcular a soma dos elementos da diagonal
// principal
for (int i = 0; i < matriz.GetLength(0); i++) {
for (int j = 0; j < matriz.GetLength(1); j++) {
if (i == j) {
soma_diagonal = soma_diagonal + matriz[i, j];
}
}
}
// finalmente mostramos a soma da diagonal principal
Console.WriteLine("\nA soma dos elementos da diagonal principal é: "
+ soma_diagonal);
Console.WriteLine("\n\nPressione qualquer tecla para sair...");
// pausa o programa
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Informe o valor para a linha 0 e coluna 0: 3 Informe o valor para a linha 0 e coluna 1: 7 Informe o valor para a linha 0 e coluna 2: 9 Informe o valor para a linha 1 e coluna 0: 2 Informe o valor para a linha 1 e coluna 1: 4 Informe o valor para a linha 1 e coluna 2: 1 Informe o valor para a linha 2 e coluna 0: 5 Informe o valor para a linha 2 e coluna 1: 6 Informe o valor para a linha 2 e coluna 2: 8 3 7 9 2 4 1 5 6 8 A soma dos elementos da diagonal principal é: 15 |
Java ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como ordenar um vetor de inteiros em ordem decrescente em JavaQuantidade de visualizações: 21069 vezes |
|
Nesta dica mostrarei como é possível ordenar um array (vetor) de ints em ordem decrescente usando o método sort() da classe Arrays e um método inverter() personalizado. É claro que há várias outras formas de se conseguir realizar esta tarefa. Espero que esta seja mais uma técnica adicionada ao seu arsenal. Veja o código Java completo:
package arquivodecodigos;
import java.util.*;
public class Estudos{
public static void main(String[] args){
// vamos declarar e construir um vetor de 5 inteiros
int[] valores = new int[5];
// inicializa os elementos do array
valores[0] = 23;
valores[1] = 65;
valores[2] = 2;
valores[3] = 87;
valores[4] = 34;
// ordena os valores
Arrays.sort(valores);
System.out.println("Ordenado em ordem crescente:");
for(int valor : valores){
System.out.print(valor + " ");
}
// vamos inverter o vetor agora
inverter(valores);
// exibe os valores dos elementos do array
// usando o laço for melhorado
System.out.println("\nOrdenado em ordem decrescente:");
for(int valor : valores){
System.out.print(valor + " ");
}
System.out.println("\n");
System.exit(0);
}
// método que recebe um array e inverte a ordem
// de seus elementos
public static void inverter(int[] b){
int esquerdo = 0;
int direito = b.length-1;
while (esquerdo < direito) {
int temp = b[esquerdo];
b[esquerdo] = b[direito];
b[direito] = temp;
esquerdo++;
direito--;
}
}
}
Ao executar este código Java nós teremos o seguinte resultado: Ordenado em ordem crescente: 2 23 34 65 87 Ordenado em ordem decrescente: 87 65 34 23 2 |
Java ::: Java para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular a norma ou módulo de vetores nos espaços R2 e R3 usando Java - Geometria Analítica e Álgebra Linear usando JavaQuantidade de visualizações: 2534 vezes |
|
Em Geometria Analítica e Álgebra Linear, a magnitude, norma, comprimento, tamanho ou módulo (também chamado de intensidade na Física) de um vetor é o seu comprimento, que pode ser calculado por meio da distância de seu ponto final a partir da origem, no nosso caso (0,0). Considere o seguinte vetor no plano, ou seja, no espaço bidimensional, ou R2: \[\vec{v} = \left(7, 6\right)\] Aqui este vetor se inicia na origem (0, 0) e vai até as coordenadas (x = 7) e (y = 6). Veja sua plotagem no plano 2D:  Note que na imagem já temos todas as informações que precisamos, ou seja, o tamanho desse vetor é 9 (arredondado) e ele faz um ângulo de 41º (graus) com o eixo x positivo. Em linguagem mais adequada da trigonometria, podemos dizer que a medida do cateto oposto é 6, a medida do cateto adjacente é 7 e a medida da hipotenusa (que já calculei para você) é 9. Note que já mostrei também o ângulo theta (__$\theta__$) entre a hipotenusa e o cateto adjacente, o que nos dá a inclinação da reta representada pelos pontos (0, 0) e (7, 6). Relembrando nossas aulas de trigonometria nos tempos do colegial, temos que o quadrado da hipotenusa é a soma dos quadrados dos catetos, ou seja, o Teorema de Pitágoras: \[a^2 = b^2 + c^2\] Como sabemos que a potenciação é o inverso da radiciação, podemos escrever essa fórmula da seguinte maneira: \[a = \sqrt{b^2 + c^2}\] Passando para os valores x e y que já temos: \[a = \sqrt{7^2 + 6^2}\] Podemos comprovar que o resultado é 9,21 (que arredondei para 9). Não se esqueça da notação de módulo ao apresentar o resultado final: \[\left|\vec{v}\right| = \sqrt{7^2 + 6^2}\] E aqui está o código Java que nos permite informar os valores x e y do vetor e obter o seu comprimento, tamanho ou módulo:
package arquivodecodigos;
import java.util.Scanner;
public class Estudos{
public static void main(String args[]){
Scanner entrada = new Scanner(System.in);
// vamos ler os valores x e y
System.out.print("Informe o valor de x: ");
double x = Double.parseDouble(entrada.nextLine());
System.out.print("Informe o valor de y: ");
double y = Double.parseDouble(entrada.nextLine());
// vamos calcular a norma do vetor
double norma = Math.sqrt(Math.pow(x, 2) + Math.pow(y, 2));
// mostra o resultado
System.out.println("A norma do vetor é: " + norma);
}
}
Ao executar este código nós teremos o seguinte resultado: Informe o valor de x: 7 Informe o valor de y: 6 A norma do vetor é: 9.219544457292887 Novamente note que arredondei o comprimento do vetor para melhor visualização no gráfico. Para calcular a norma de um vetor no espaço, ou seja, no R3, basta acrescentar o componente z no cálculo. |
JavaScript ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como adicionar um ou mais elementos ao início de um vetor JavaScript usando o método unshift() do objeto Array - [Revisado]Quantidade de visualizações: 7225 vezes |
O método unshift(), presente no JavaScript desde sua versão 1.2, é usado quando queremos adicionar um ou mais elementos no início de um vetor (array). Veja:
<script type="text/javascript">
var valores = new Array(1, 2, 3, 4, 5);
document.write("Valores no vetor: " + valores + "<br>");
valores.unshift(6);
document.write("Novos valores no vetor: " + valores);
</script>
Aqui nós adicionamos o valor 6 no início do vetor. Veja agora como adicionar três valores no início do vetor:
<script type="text/javascript">
var valores = new Array(1, 2, 3, 4, 5);
window.alert("Valores no vetor: " + valores);
valores.unshift(6, 7, 8);
window.alert("Novos valores no vetor: " + valores);
</script>
É importante observar que a função unshift() modifica o vetor original, e seu retorno é a nova quantidade de elementos no vetor. |
React Native ::: React Native - Componentes Visuais ::: Button |
Como detectar um clique em um botão do React Native e exibir uma mensagem AlertQuantidade de visualizações: 1366 vezes |
|
Nesta dica mostrarei como detectar um evento onPress em um botão do React Native e exibir uma mensagem usando o método alert() do componente Alert. Note que o evento onPress é disparado quando o usuário pressiona o botão. Veja o código completo para o exemplo:
import React, {Component} from 'react';
import {View, Button, Alert} from 'react-native';
type Props = {};
export default class App extends Component<Props> {
render() {
return (
<View style={{backgroundColor: '#eeeeee',
padding: 30}}>
<Button onPress = {() =>
Alert.alert("Bem-vindo(a) ao React Native")}
title="Clique" />
</View>
);
}
}
Veja que este exemplo define o código a ser chamado quando o botão for clicado diretamente em sua declaração. Em outras dicas dessa seção você verá como clicar no botão e chamar uma função JavaScript residente fora da declaração do botão. |
Java ::: Dicas & Truques ::: MIDI Musical Instrument Digital Interface, Mapeamento e sequenciamento MIDI, Entrada e saída MIDI |
Java para músicos - Como escrever um MIDI Player em Java (código bem simples e fácil de entender)Quantidade de visualizações: 13974 vezes |
|
Nesta dica apresento uma aplicação completa para um MIDI Player em Java. Trata-se de uma aplicação console que você pode estudar e implementar a mesma idéia em Java Swing ou JavaFX. Para executar o código abaixo, você só precisa definir o caminho e nome de um arquivo MIDI (extensão .mid). Veja o código completo e divirta-se:
package arquivodecodigos;
import javax.sound.midi.*;
import java.io.*;
public class Estudos{
public static void main(String args[]) {
// nome do arquivo MIDI
String arquivo = "amazing_grace.mid";
if(!arquivo.endsWith(".mid")) {
System.out.println("Este não parece ser um arquivo MIDI válido.");
System.exit(1);
}
File midiFile = new File(arquivo);
if(!midiFile.exists() || midiFile.isDirectory() ||
!midiFile.canRead()) {
System.out.println("Não foi possível acessar o arquivo indicado.");
System.exit(1);
}
try{
Sequencer seq = MidiSystem.getSequencer();
seq.setSequence(MidiSystem.getSequence(midiFile));
seq.open();
seq.start();
while(true){
if(seq.isRunning()){
try{
Thread.sleep(1000);
}
catch(InterruptedException ignore){
break;
}
}
else{
break;
}
}
seq.stop();
seq.close();
}
catch(MidiUnavailableException mue){
System.out.println("Dispositivo de MIDI indisponível");
}
catch(InvalidMidiDataException imde){
System.out.println("Dados MIDI Inválidos");
}
catch(IOException ioe){
System.out.println("Erro de I/O");
}
}
}
|
C# ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como ordenar um array de strings em ordem alfabética em C# usando a classe StringComparerQuantidade de visualizações: 17649 vezes |
|
Nesta dica mostrarei como classificar um vetor de strings C# em ordem alfabética. Para isso nós vamos usar um objeto da classe StringComparer. Veja o código completo para o exemplo:
using System;
namespace Estudos {
class Program {
static void Main(string[] args) {
// cria e inicializa um array de strings
string[] cidades = {"Goiânia", "São Paulo",
"Rio de Janeiro", "Curitiba"};
Console.WriteLine("Ordem original:");
for (int i = 0; i < cidades.Length; i++) {
Console.WriteLine(cidades[i]);
}
// vamos criar um objeto da classe StringComparer
StringComparer ordenar = StringComparer.CurrentCultureIgnoreCase;
// agora classificamos o vetor em ordem alfabética
Array.Sort(cidades, ordenar);
Console.WriteLine();
Console.WriteLine("Ordem alfabética:");
for (int i = 0; i < cidades.Length; i++) {
Console.WriteLine(cidades[i]);
}
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código C# nós teremos o seguinte resultado: Ordem original: Goiânia São Paulo Rio de Janeiro Curitiba Ordem alfabética: Curitiba Goiânia Rio de Janeiro São Paulo |
Delphi ::: Classes, Controles e Componentes ::: TRegistry (Registro do Windows) |
Como excluir chaves no registro do Windows usando Delphi a função DeleteKey() da classe TRegistry do DelphiQuantidade de visualizações: 14128 vezes |
|
Em algumas situações precisamos excluir determinadas chaves do registro do Windows. Para isso podemos usar o método DeleteKey() da classe TRegistry. Este método recebe uma string especificando a chave a ser excluída e retorna um valor Boolean, informando o sucesso da operação. Veja um trecho de código no qual tentamos excluir uma chave com o nome de "Arquivo de Códigos" localizada sob a chave raiz HKEY_CURRENT_USER:
procedure TForm3.Button5Click(Sender: TObject);
var
reg: TRegistry;
begin
// uses Registry
// vamos criar uma instância da classe TRegistry
reg := TRegistry.Create;
// a chave raiz padrão é HKEY_CURRENT_USER mas, por via das dúvidas
// vamos reafirmar isso
reg.RootKey := HKEY_CURRENT_USER;
// vamos verificar se a chave que estamos querendo excluir
// existe
if reg.KeyExists('Arquivo de Códigos') then
begin
// a chave foi encontrada? vamos excluir
if reg.DeleteKey('Arquivo de Códigos') then
begin
ShowMessage('A chave foi excluída com sucesso.');
end
else
begin
ShowMessage('Não consegui excluir a chave especificada');
end;
end
else
begin
ShowMessage('A chave que você deseja excluir não foi encontrada.');
end;
// vamos liberar o registro
reg.Free;
end;
Note que este método remove a chave e todas as informações associadas a ela. Porém, se a chave possuir sub-chaves, estas deverão ser removidas individualmente antes de excluirmos a chave mãe. Para fins de compatibilidade, esta dica foi escrita usando Delphi 2009. |
C++ ::: Dicas & Truques ::: Matemática e Estatística |
Como calcular desvio padrão em C++ - C++ para Matemática e EstatísticaQuantidade de visualizações: 924 vezes |
|
Em Matemática e Estatística, o Desvio padrão (em inglês: Standard Deviation) é uma medida de dispersão, ou seja, é uma medida que indica o quanto um conjunto de dados é uniforme. Quando o desvio padrão é baixo, isso quer dizer que os dados do conjunto estão mais próximos da média. Como calcular o desvio padrão de um conjunto de dados? Vamos começar analisando a fórmula mais difundida na matemática e na estatística: \[\sigma = \sqrt{ \frac{\sum_{i=1}^N (x_i -\mu)^2}{N}}\] Onde: a) __$\sigma__$ é o desvio; b) __$x_i__$ é um valor qualquer no conjunto de dados na posição i; c) __$\mu__$ é a média aritmética dos valores do conjunto de dados; d) N é a quantidade de valores no conjunto. O somatório dentro da raiz quadrada nos diz que devemos somar todos os elementos do conjunto, desde a posição 1 até a posição n, subtrair cada valor pela média do conjunto e elevar ao quadrado. Obtida a soma, nós a dividimos pelo tamanho do conjunto. Veja o código C++ completo que obtém o desvio padrão a partir de um conjunto de dados contendo quatro valores:
#include <iostream>
#include <math.h>
using namespace std;
// função principal do programa
int main(int argc, char *argv[]){
// conjunto dos dados
double conjunto[] = {10, 30, 90, 30};
double soma = 0.0; // soma dos elementos
double desvio_padrao = 0.0; // desvio padrão
int tam = 4; // tamanho dos dados
double media;
// vamos somar todos os elementos
for(int i = 0; i < tam; i++){
soma = soma + conjunto[i];
}
// agora obtemos a média do conjunto de dados
media = soma / tam;
// e finalmente obtemos o desvio padrão
for(int i = 0; i < tam; i++){
desvio_padrao = desvio_padrao + pow(conjunto[i] - media, 2);
}
// mostramos o resultado
cout << "Desvio Padrão Populacional: " << sqrt(desvio_padrao / tam);
cout << "\nDesvio Padrão Amostral: " << sqrt(desvio_padrao / (tam - 1));
cout << "\n" << endl;
system("PAUSE"); // pausa o programa
return EXIT_SUCCESS;
}
Ao executar este código C++ nós teremos o seguinte resultado: Desvio Padrão Populacional: 30.0 Desvio Padrão Amostral: 34.64101615137755 Veja que, para calcular o Desvio Padrão Populacional, nós dividimos o somatório pela quantidade de elementos no conjunto, enquanto, para calcular o Desvio Padrão Amostral, nós dividimos o somatório pela quantidade de elementos - 1 (cuidado com a divisão por zero no caso de um conjunto com apenas um elemento). |
Nossas 20 dicas & truques de programação mais populares |
|
C# - Como detectar a mudança de estado da CheckBox do C# Windows Forms usando o evento CheckedChanged Dart - Como testar se um ponto está dentro de um círculo em Dart - Desenvolvimento de Games com Dart |
Você também poderá gostar das dicas e truques de programação abaixo |
|
Java - Estruturas de Dados em Java - Como inserir nós no final de uma lista singularmente ligada em Java JavaScript - Como converter uma string para letras minúsculas em JavaScript usando a função toLowerCase() do objeto String |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





