Java ::: Pacote java.lang ::: StringBuffer |
Java do básico ao avançado - Como usar o método append() para adicionar mais conteúdo ao final de um StringBufferQuantidade de visualizações: 9438 vezes |
|
O método append() da classe StringBuffer se torna útil quando precisamos adicionar mais conteúdo ao final de um objeto desta classe. Este método possui, no Java 7, as seguintes sobrecargas: public StringBuffer append(Object obj) public StringBuffer append(String str) public StringBuffer append(StringBuffer sb) public StringBuffer append(CharSequence s) public StringBuffer append(CharSequence s, int start, int end) public StringBuffer append(char[] str) public StringBuffer append(char[] str, int offset, int len) public StringBuffer append(boolean b) public StringBuffer append(char c) public StringBuffer append(int i) public StringBuffer append(long lng) public StringBuffer append(float f) public StringBuffer append(double d) Note que em todas as sobrecargas do método, o retorno é um objeto da classe StringBuffer. Mas, não é um novo objeto StringBuffer. É uma referência ao objeto StringBuffer já existente. Veja um exemplo no qual usamos este método para adicionar mais duas palavras ao conteúdo do StringBuffer:
package estudos;
public class Estudos{
public static void main(String[] args) {
// um StringBuffer contendo uma frase
StringBuffer frase = new StringBuffer("Gosto muito de programar");
// vamos adicionar mais duas palavras ao final do StringBuffer
frase.append(" em");
frase.append(" Java");
// agora mostramos o resultado
System.out.println(frase);
System.exit(0);
}
}
Ao executarmos este código nós teremos o seguinte resultado: Gosto muito de programar em Java |
Java ::: Java para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como converter Coordenadas Cartesianas para Coordenadas Polares usando Java - Java para EngenhariaQuantidade de visualizações: 2196 vezes |
|
Nesta nossa série de Java para Geometria Analítica e Álgebra Linear, mostrarei um código 100% funcional para fazer a conversão entre coordenadas cartesianas e coordenadas polares. Esta operação é muito frequente em computação gráfica e é parte integrante das disciplinas dos cursos de Engenharia (com maior ênfase na Engenharia Civil). Na matemática, principalmente em Geometria e Trigonometria, o sistema de Coordenadas no Plano Cartesiano, ou Espaço Cartesiano, é um sistema que define cada ponto em um plano associando-o, unicamente, a um conjuntos de pontos numéricos. Dessa forma, no plano cartesiano, um ponto é representado pelas coordenadas (x, y), com o x indicando o eixo horizontal (eixo das abscissas) e o y indicando o eixo vertical (eixo das ordenadas). Quando saímos do plano (espaço 2D ou R2) para o espaço (espaço 3D ou R3), temos a inclusão do eixo z (que indica profundidade). Já o sistema de Coordenadas Polares é um sistema de coordenadas em duas dimensões no qual cada ponto no plano é determinado por sua distância a partir de um ponto de referência conhecido como raio (r) e um ângulo a partir de uma direção de referência. Este ângulo é normalmente chamado de theta (__$\theta__$). Assim, um ponto em Coordenadas Polares é conhecido por sua posição (r, __$\theta__$). Antes de prosseguirmos, veja uma imagem demonstrando os dois sistemas de coordenadas: 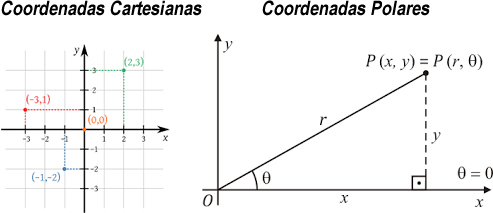 A fórmula para conversão de Coordenadas Cartesianas para Coordenadas Polares é: __$r = \sqrt{x^2+y2}__$ __$\theta = \\arctan\left(\frac{y}{x}\right)__$ E aqui está o código Java completo que recebe as coordenadas cartesianas (x, y) e retorna as coordenadas polares (r, __$\theta__$):
package arquivodecodigos;
import java.util.Scanner;
public class Estudos{
public static void main(String args[]){
Scanner entrada = new Scanner(System.in);
// vamos ler as coordenadas cartesianas
System.out.print("Valor de x: ");
double x = Double.parseDouble(entrada.nextLine());
System.out.print("Valor de y: ");
double y = Double.parseDouble(entrada.nextLine());
// vamos calcular o raio
double raio = Math.sqrt(Math.pow(x, 2) + Math.pow(y, 2));
// agora calculamos o theta (ângulo) em radianos
double theta = Math.atan2(y, x);
// queremos o ângulo em graus também
double angulo_graus = 180 * (theta / Math.PI);
// e exibimos o resultado
System.out.println("As Coordenadas Polares são:\n" +
"raio = " + raio + ", theta = " + theta + ", ângulo em graus = " +
angulo_graus);
}
}
Ao executar este código nós teremos o seguinte resultado: Valor de x: -1 Valor de y: 1 As Coordenadas Polares são: raio = 1.4142135623730951, theta = 2.356194490192345, ângulo em graus = 135.0 Veja que as coordenadas polares equivalentes são (__$\sqrt{2}__$, __$\frac{3\pi}{4}__$), com o theta em radianos. Sim, os professores das disciplinas de Geometria Analítica e Álgebra Linear, Física e outras gostam de escrever os resultados usando raizes e frações em vez de valores reais. |
Delphi ::: Dicas & Truques ::: Arrays e Matrix (Vetores e Matrizes) |
Como usar arrays (vetores e matrizes) em DelphiQuantidade de visualizações: 73686 vezes |
|
Em programação de computadores, um array, também conhecido como vector (para arrays uni-dimensionais) ou matriz (para arrays bi-dimensionais), é uma das mais simples estruturas de dados. Os arrays mantêm uma série de elementos de dados, geralmente do mesmo tamanho e tipo de dados. Elementos individuais são acessados por sua posição no array. A posição é dada por um índice, também chamado de subscrição. O índice geralmente utiliza uma seqüência de números inteiros, (ao contrário de um array associativo) mas o índex pode ter qualquer valor ordinal. Alguns arrays são multi-dimensionais, significando que eles são indexados por um número fixo de números inteiros, por exemplo, por um seqüência (ou sucessão) finita de quatro números inteiros. Geralmente, arrays uni- e bi-dimensionais são os mais comuns. Os arrays podem ser considerados como as estruturas de dado mais simples que é possível imaginar. Têm a vantagem de que os seus elementos são acessíveis de forma rápida, mas têm uma notável limitação: são de tamanho fixo, mas podem ser incrementados ou diminuídos com determinados algoritmos, geralmente envolvendo a cópia de elementos de um array para outro e reinicializando o original com a nova dimensão. Os vetores podem ser implementados desta forma. Em Delphi um array é declarado da seguinte forma: var valores: array[1..10] of Integer; Aqui nós temos um array chamado valores que contém 10 elementos do tipo Integer. Estes elementos podem ser acessados por índices que variarão de 1 a 10, ou seja, podemos acessar o 5º elemento da seguinte forma: procedure TForm1.Button1Click(Sender: TObject); var valores: array[1..10] of Integer; begin valores[5] := 20; end; Este tipo de array que ora criamos é chamado de array estático, em contraposição aos arrays dinâmicos, os quais podem ter seus tamanhos redimensionados durante a execução do programa. A forma mais prática de se trabalhar com arrays em Delphi é usando laços. Veja:
procedure TForm1.Button1Click(Sender: TObject);
var
valores: array[1..5] of Integer;
i, soma: Integer;
begin
// vamos preencher o array com os valores de 1 a 5
for i := 1 to 5 do
begin
valores[i] := i;
end;
// vamos percorrer o array novamente e obter a soma dos
// valores de seus elementos
soma := 0;
for i := 1 to 5 do
begin
soma := soma + valores[i];
end;
// vamos exibir o resultado
ShowMessage('A soma dos valores é: ' + IntToStr(soma));
end;
Aqui nós declaramos um array de 5 elementos do tipo Integer e inicializamos seus elementos com os valores de 1 a 5. Em seguida percorremos todo o array novamente para obter a soma dos valores dos elementos. É possível também declarar e já inicializar um array. Veja:
procedure TForm1.Button1Click(Sender: TObject);
const
valores: array[1..5] of Integer = (3, 2, 6, 12, 9);
var
i, soma: Integer;
begin
// vamos percorrer o array novamente e obter a soma dos
// valores de seus elementos
soma := 0;
for i := 1 to 5 do
begin
soma := soma + valores[i];
end;
// vamos exibir o resultado
ShowMessage('A soma dos valores é: ' + IntToStr(soma));
end;
Note que aqui eu declarei o array como uma constante. Isso aconteceu porque o Delphi não permite que inicializemos variáveis locais ([DCC Error] Unit1.pas(32): E2195 Cannot initialize local variables). Caso você realmente precise do array como variável e não constante, e deseje inicializá-lo juntamente com a declaração, mova-o para a seção interface do formulário ou classe. Para finalizar, veja que é possível criar arrays de todos os tipos em Delphi. Veja no trecho de código abaixo como usamos um array de Char para guardar uma palavra e exibí-la normal e depois invertida:
procedure TForm1.Button1Click(Sender: TObject);
const
letras: array[1..5] of Char = ('O', 's', 'm', 'a', 'r');
var
i: Integer;
resultado: String;
begin
resultado := '';
// vamos exibir a palavra na forma normal
for i := 1 to 5 do
resultado := resultado + letras[i];
// exibe o resultado
ShowMessage(resultado);
// vamos exibir a palavra invertida
resultado := '';
for i := 5 downto 1 do
resultado := resultado + letras[i];
// exibe o resultado
ShowMessage(resultado);
end;
Para fins de compatibilidade, esta dica foi escrita usando Delphi 2009. |
Delphi ::: Data Controls (Controles de Dados) ::: TDBGrid |
Como obter o índice da linha da célula atual em um TDBGrid do DelphiQuantidade de visualizações: 9948 vezes |
|
Como obter o índice da linha da célula atual (com foco) em um TDBGrid do Delphi Em algumas situações precisamos obter o índice da linha da célula atual, ou seja, a célula que detém o foco no momento em um TDBGrid. Isso pode ser feito por meio da propriedade Row da classe TCustomGrid (e publicada na classe TStringGrid). Como esta propriedade não está publicada na classe TDBGrid (Delphi 2009), o que fazemos é um casting para a classe TStringGrid. Veja um trecho de código no qual usamos o evento Click de um botão para informar o índice da linha da célula atual:
procedure TForm3.Button3Click(Sender: TObject);
var
indice: Integer;
begin
// vamos obter o índice da linha da célula atual
indice := TStringGrid(DBGrid1).Row;
ShowMessage('O índice da linha da célula atual é: ' +
IntToStr(indice));
end;
Execute o código e clique no botão. Você verá uma mensagem parecida com: "O índice da linha da célula atual é: 4". Lembre-se de que o índice da linha fixa do DBGrid é 0. Esta dica foi escrita e testada no Delphi 2009. |
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Laços de Repetição |
Exercícios Resolvidos de Java - Escreva um programa (algorítmo) Java que usa o laço for para exibir uma tabela de conversões de milhas para quilômetrosQuantidade de visualizações: 3907 vezes |
|
Pergunta/Tarefa: Escreva um programa (algorítmo) Java que usa o laço for para exibir uma tabela de conversões de milhas para quilômetros. Sabendo que uma milha equivale a 1.609 quilômetros, seu programa deverá exibir uma saída parecida com: Milhas Quilômetros ------------------------------- 1 1.609 2 3.218 3 4.827 4 6.436 5 8.045 6 9.654 7 11.263 8 12.872 9 14.481 10 16.09 Veja a resolução comentada deste exercício usando Java console:
package estudos;
public class Estudos {
public static void main(String[] args){
System.out.println("Milhas\t\tQuilômetros");
System.out.println("-------------------------------");
// um laço for que repetirá 10 vezes
for (int i = 1; i <= 10; i++){
// usamos a variável de controle do laço para o cálculo
System.out.println(i + "\t\t" + (i * 1.609));
}
}
}
|
Python ::: Python para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como converter Coordenadas Cartesianas para Coordenadas Polares usando PythonQuantidade de visualizações: 5801 vezes |
|
Nesta nossa série de Python para Geometria Analítica e Álgebra Linear, mostrarei um código 100% funcional para fazer a conversão entre coordenadas cartesianas e coordenadas polares. Esta operação é muito frequente em computação gráfica e é parte integrante das disciplinas dos cursos de Engenharia (com maior ênfase na Engenharia Civil). Na matemática, principalmente em Geometria e Trigonometria, o sistema de Coordenadas no Plano Cartesiano, ou Espaço Cartesiano, é um sistema que define cada ponto em um plano associando-o, unicamente, a um conjuntos de pontos numéricos. Dessa forma, no plano cartesiano, um ponto é representado pelas coordenadas (x, y), com o x indicando o eixo horizontal (eixo das abscissas) e o y indicando o eixo vertical (eixo das ordenadas). Quando saímos do plano (espaço 2D ou R2) para o espaço (espaço 3D ou R3), temos a inclusão do eixo z (que indica profundidade). Já o sistema de Coordenadas Polares é um sistema de coordenadas em duas dimensões no qual cada ponto no plano é determinado por sua distância a partir de um ponto de referência conhecido como raio (r) e um ângulo a partir de uma direção de referência. Este ângulo é normalmente chamado de theta (__$\theta__$). Assim, um ponto em Coordenadas Polares é conhecido por sua posição (r, __$\theta__$). Antes de prosseguirmos, veja uma imagem demonstrando os dois sistemas de coordenadas:  A fórmula para conversão de Coordenadas Cartesianas para Coordenadas Polares é: __$r = \sqrt{x^2+y2}__$ __$\theta = \\arctan\left(\frac{y}{x}\right)__$ E aqui está o código Python completo que recebe as coordenadas cartesianas (x, y) e retorna as coordenadas polares (r, __$\theta__$):
# importamos a bibliteca NumPy
import numpy as np
import math as math
def main():
# vamos ler as coordenadas cartesianas
x = float(input("Valor de x: "))
y = float(input("Valor de y: "))
# vamos calcular o raio
raio = math.sqrt(math.pow(x, 2) + math.pow(y, 2))
# agora calculamos o theta (ângulo) em radianos
theta = np.arctan2(y, x)
# queremos o ângulo em graus também
angulo_graus = 180 * (theta / math.pi)
# e exibimos o resultado
print("As Coordenadas Polares são:")
print("raio = %0.4f, theta = %0.4f, ângulo em graus = %0.2f"
% (raio, theta, angulo_graus))
if __name__== "__main__":
main()
Ao executar este código nós teremos o seguinte resultado: Valor de x: -1 Valor de y: 1 As Coordenadas Polares são: raio = 1.4142, theta = 2.3562, ângulo em graus = 135.00 Veja que as coordenadas polares equivalentes são (__$\sqrt{2}__$, __$\frac{3\pi}{4}__$), com o theta em radianos. Sim, os professores das disciplinas de Geometria Analítica e Álgebra Linear, Física e outras gostam de escrever os resultados usando raízes e frações em vez de valores reais. |
Delphi ::: VCL - Visual Component Library ::: TEdit |
Como obter a quantidade de caracteres no texto de um TEdit do Delphi usando a função SendMessage() da API do Windows e a mensagem WM_GETTEXTLENGTHQuantidade de visualizações: 11085 vezes |
|
Em algumas ocasiões gostaríamos de obter o tamanho do texto de um TEdit usando apenas as funções da API do Windows. Para isso podemos usar a função SendMessage() em combinação com a mensagem WM_GETTEXTLENGTH. A função SendMessage() da API do Windows possui a seguinte assinatura em C/C++: LRESULT SendMessage( HWND hWnd, UINT Msg, WPARAM wParam, LPARAM lParam ); No arquivo Windows.pas podemos encontrar o protótipo e corpo desta função convertidos para Object Pascal:
// Protótipo
{$EXTERNALSYM SendMessage}
function SendMessage(hWnd: HWND; Msg: UINT; wParam: WPARAM;
lParam: LPARAM): LRESULT; stdcall;
// Implementação
function SendMessage; external user32 name 'SendMessageW';
Quando usamos a mensagem WM_GETTEXTLENGTH para obter a quantidade de caracteres no texto de um TEdit, o retorno da função SendMessage() é um valor inteiro contendo a quantidade de caracteres na caixa de texto. Os parâmetros wParam e lParam não são usados, ou seja, podemos fornecer o valor 0 para os mesmos. Veja:
procedure TForm1.Button1Click(Sender: TObject);
var
tamanho: Integer;
begin
// vamos obter a quantidade de caracteres na caixa de texto
tamanho := SendMessage(Edit1.Handle, WM_GETTEXTLENGTH, 0, 0);
// vamos exibir o resultado
ShowMessage('O edit contém ' + IntToStr(tamanho) + ' caracteres.');
end;
Ao executar este exemplo teremos uma mensagem com um conteúdo parecido com: O edit contém 10 caracteres. |
Python ::: Python para Engenharia ::: Engenharia Civil - Cálculo Estrutural |
Como calcular o Momento Fletor Mínimo e a Excentricidade Mínima de 1ª Ordem de um pilar em Python - Python para Engenharia Civil e Cálculo EstruturalQuantidade de visualizações: 572 vezes |
 O cálculo e dimensionamento de pilares, sejam pilares de canto, extremidade ou intermediários, sempre seguem alguns passos cujas ordens são muito importantes, pois os dados de entrada de um passo podem vir de um ou mais passos anteriores. Em dicas anteriores do uso da linguagem Python no cálculo de pilares eu mostrei como calcular os esforços solicitantes majorados em pilares e também como calcular o índice de esbeltez de um pilar nas direções x e y. Nesta dica mostrarei como calcular o Momento Fletor Mínimo e a Excentricidade Mínima de 1ª Ordem de um pilar. Estes dados são muito importantes para a aplicação das fórmulas que embasam a área de aço a ser usada no pilar. Note que a Excentricidade Mínima de 1ª Ordem pode ser desprezada no caso de pilares intermediários (também chamados pilares de centro). O Momento Fletor Mínimo é o momento mínimo que deve ser considerado, mesmo em pilares nos quais a carga está centrada, e é calculado por meio da seguinte fórmula: \[M_\text{1d,min} = Nd \cdot (1,5 + (0,03 \cdot h) \] Onde: M1d,min é o momento fletor mínimo na direção x ou y em kN.cm. Nd são os esforços solicitantes majorados em kN. h é a dimensão do pilar na direção considerada (x ou y) em cm. A Excentricidade Mínima de 1ª Ordem do pilar pode ser calculada por meio da fórmula: \[e_\text{1,min} = \frac{M_\text{1d,min}}{Nd} \] Onde: e1,min é excentricidade mínima de 1ª ordem na direção escolhida. Nd são os esforços solicitantes majorados em kN. Note que, a exemplo do momento fletor mínimo, a excentricidade mínima de 1ª ordem também deve ser calculada nas direções x e y do pilar. Vamos ao código Python agora? Veja que o código pede para o usuário informar as dimensões do pilar nas direções x e y em centímetros, a carga total que chega ao pilar em kN e mostra o momento fletor mínimo e a excentricidade mínima de 1ª ordem no pilar, tanto na direção x quanto na direção y:
# método principal
def main():
# vamos pedir as dimensões do pilar
hx = float(input("Informe a dimensão do pilar na direção x (em cm): "))
hy = float(input("Informe a dimensão do pilar na direção y (em cm): "))
# vamos pedir a carga total no pilar em kN
Nk = float(input("Informe a carga total no pilar (em kN): "))
# vamos obter o menor lado do pilar (menor dimensão da seção transversal)
if (hx < hy):
b = hx
else:
b = hy
# agora vamos calcular a área do pilar em centímetros quadrados
area = hx * hy
# a área está de acordo com a norma NBR 6118 (ABNT, 2014)
if (area < 360):
print("A área do pilar não pode ser inferior a 360cm2")
return
# vamos calcular a força normal de projeto Nd
yn = 1.95 - (0.05 * b) # de acordo com a norma NBR 6118 (ABNT, 2014) Tabela 13.1
yf = 1.4 # regra geral para concreto armado
Nd = yn * yf * Nk
# e agora vamos calcular o momento fletor mínimo na direção x do pilar
M1d_min_x = Nd * (1.5 + (0.03 * hx))
# e agora vamos calcular o momento fletor mínimo na direção y do pilar
M1d_min_y = Nd * (1.5 + (0.03 * hy))
# agora vamos calcular a excentricidade mínima de 1ª ordem na direção x do pilar
e1x_min = M1d_min_x / Nd
# e finalmente a excentricidade mínima de 1ª ordem na direção y do pilar
e1y_min = M1d_min_y / Nd
# e mostramos os resultados
print("\nO momento fletor mínimo na direção x é: {0} kN.cm".format(
round(M1d_min_x, 2)))
print("O momento fletor mínimo na direção y é: {0} kN.cm".format(
round(M1d_min_y, 2)))
print("A excentricidade mínima de 1ª ordem na direção x é: {0} cm".format(
round(e1x_min, 2)))
print("A excentricidade mínima de 1ª ordem na direção y é: {0} cm".format(
round(e1y_min, 2)))
if __name__== "__main__":
main()
Ao executar este código Python nós teremos o seguinte resultado: Informe a dimensão do pilar na direção x (em cm): 40 Informe a dimensão do pilar na direção y (em cm): 19 Informe a carga total no pilar (em kN): 841.35 O momento fletor mínimo na direção x é: 3180.3 kN.cm O momento fletor mínimo na direção y é: 2438.23 kN.cm A excentricidade mínima de 1ª ordem na direção x é: 2.7 cm A excentricidade mínima de 1ª ordem na direção y é: 2.07 cm |
Python ::: Desafios e Lista de Exercícios Resolvidos ::: Python Básico |
Exercícios Resolvidos de Python - Como testar se um número é potência de dois usando PythonQuantidade de visualizações: 741 vezes |
|
Pergunta/Tarefa: Escreva um programa Python contendo um método que recebe um número inteiro e retorna um valor boolean indicando se o valor informado é potência de dois. Sua saída deverá ser parecida com: Informe um valor inteiro: 8 O valor 8 é potência de dois Informe um valor inteiro: 34 O valor 34 não é potência de dois Informe um valor inteiro: 64 O valor 64 é potência de dois Veja a resolução comentada deste exercício usando Python:
# método que recebe um número inteiro e informe se ele é
# potência de dois
def is_potencia_dois(n):
# usamos o operador AND de bits para verificar se n AND n-1
# é igual a 0
return (n > 0) and (n & (n - 1)) == 0
# método principal
def main():
# vamos pedir para o usuário informar um valor inteiro
valor = int(input("Informe um valor inteiro: "))
# vamos testar se o número informado é potência de dois
if is_potencia_dois(valor):
print("O valor {0} é potência de dois".format(valor))
else:
print("O valor {0} não é potência de dois".format(valor))
if __name__== "__main__":
main()
|
Java ::: Desafios e Lista de Exercícios Resolvidos ::: Java Básico |
Exercício Resolvido de Java - Como calcular o Índice de Massa Corporal em Java - Como calcular IMC em JavaQuantidade de visualizações: 12676 vezes |
|
Pergunta/Tarefa: O índice de massa corporal (IMC) é uma medida internacional usada para calcular se uma pessoa está no peso ideal. Ele foi desenvolvido pelo polímata Lambert Quételet no fim do século XIX. Trata-se de um método fácil e rápido para a avaliação do nível de gordura de cada pessoa, ou seja, é um preditor internacional de obesidade adotado pela Organização Mundial da Saúde (OMS). O IMC é determinado pela divisão da massa do indivíduo pelo quadrado de sua altura, em que a massa está em quilogramas e a altura em metros. A fórmula é a seguinte:  A classificação é feita de acordo com as seguintes regras: a) < 16 - Magreza grave b) 16 a < 17 - Magreza moderada c) 17 a < 18,5 - Magreza leve d) 18,5 a < 25 - Saudável e) 25 a < 30 - Sobrepeso f) 30 a < 35 - Obesidade Grau I g) 35 a < 40 - Obesidade Grau II (severa) h) >= 40 - Obesidade Grau III (mórbida) Escreva um programa Java que leia o peso e a altura de uma pessoa e retorna seu IMC classificado de acordo com a tabela acima. Sua saída deverá ser parecida com: Informe seu peso: 82 Informe sua altura: 1.85 Seu IMC é: 23.959094229364496 Sua classificação é Saudável Veja a resolução comentada deste exercício usando Java:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
Scanner entrada = new Scanner(System.in);
// vamos solicitar o peso e a altura da pessoa
System.out.print("Informe seu peso: ");
double peso = Double.parseDouble(entrada.nextLine());
System.out.print("Informe sua altura: ");
double altura = Double.parseDouble(entrada.nextLine());
// vamos calcular o IMC
double imc = peso / (altura * altura);
System.out.println("Seu IMC é: " + imc);
// vamos mostrar a classificação
if(imc < 16){
System.out.println("Sua classificação é Magreza grave");
}
else if((imc >= 16) && (imc < 17)){
System.out.println("Sua classificação é Magreza moderada");
}
else if((imc >= 17) && (imc < 18.5)){
System.out.println("Sua classificação é Magreza leve");
}
else if((imc >= 18.5) && (imc < 25)){
System.out.println("Sua classificação é Saudável");
}
else if((imc >= 25) && (imc < 30)){
System.out.println("Sua classificação é Sobrepeso");
}
else if((imc >= 30) && (imc < 35)){
System.out.println("Sua classificação é Obesidade Grau I");
}
else if((imc >= 35) && (imc < 40)){
System.out.println("Sua classificação é Obesidade Grau II");
}
else{
System.out.println("Sua classificação é Obesidade Grau III (mórbida)");
}
System.out.println("\n");
}
}
|
Nossas 20 dicas & truques de programação mais populares |
|
Portugol - Como calcular o coeficiente angular de uma reta em Portugol dados dois pontos no plano cartesiano VB.NET - Como retornar o tamanho de uma string em VB.NET usando a propriedade Length da classe String |
Você também poderá gostar das dicas e truques de programação abaixo |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |






