Delphi ::: Dicas & Truques ::: Bilbiotecas Estáticas (obj) e Dinâmicas (DLLs) |
Como criar DLLs usando Delphi? É possível criar DLLs para o Windows usando Delphi?Quantidade de visualizações: 13050 vezes |
|
As DLLs (Dynamic Link Libraries - Bibliotecas de Vínculo Dinâmico) são arquivos compilados bem similares aos arquivos .exe que estamos acostumados a criar em Delphi. Uma DLL contém rotinas, recursos ou ambos. Mas, não pode ser executada por si só, ou seja, se dermos duplo-clique em uma DLL nada acontecerá. Isso acontece porque uma DLL é desenvolvida para ser usada juntamente como outros aplicativos e/ou outras DLLs. No ambiente Windows encontramos muitas DLLs. Na verdade, o Windows e sua Win32 API é uma coleção de DLLs. Se olharmos nos diretórios System ou System32 encontraremos várias delas, incluindo kernel32.dll, gdi32.dll, user32.dll, shell32.dll, comctl32.dll, entre outras. Mas, para que servem as DLLs? É possível desenvolver aplicações Windows sem usá-las? Vamos às respostas. As DLLs existem com o propósito de compartilhar código entre aplicações. Isso quer dizer que uma mesma DLL pode estar sendo usada por vários programas ao mesmo tempo. E isso é verdade no ambiente Windows. Todos os programas de interface gráfica escritos em Delphi, C, C++, etc e que usam os componentes gráficos do Windows estão de alguma forma fazendo uso de códigos disponíveis em DLLs do sistema. Sem o aproveitamente de tais códigos os executáveis ficariam enormes, visto que cada um teria que implementar as rotinas de desenho e diretivas de criação de janelas. Ao aproveitar as funcionalidades disponíveis nas DLLs do sistema esta tarefa se torna muito mais fácil. Mas, além de usar DLLs de terceiros com códigos já prontos e devidamente testados, você também pode criar suas próprias DLLs. O motivo disso é que você pode querer compartilhar algumas de suas rotinas entre os vários aplicativos que você desenvolve. A maior vantagem disso é que, ao atualizar ou corrigir o código em uma DLL você estará certo de que todas as aplicações que fazem uso desta DLL automaticamente perceberão e tirarão proveito da atualização. Entre as vantagens do uso de DLLs podemos citar: a) Podemos compartilhar rotinas e códigos entre várias aplicativos; b) Ao mantermos boa parte de nossos códigos em DLLs nós conseguimos economizar memória e espaço em disco; c) Outros desenvolvedores poderão usar nossas rotinas e lógica mesmo sem ter acesso aos nossos códigos-fontes; d) Podemos usar códigos escritos em outras linguagens em nossos programas Delphi. Isso quer dizer que uma DLL escrita em C/C++ poderá ser usada em um programa Delphi sem qualquer problema. A prova disso é que as DLLs do Windows são escritas em C/C++. Hora de criar sua primeira DLL em Delphi. Consulte outras dicas nesta seção para aprender a fazê-lo. Para fins de compatibilidade, esta dica foi escrita usando Delphi 2009. |
Firebird ::: Dicas & Truques ::: Strings e Caracteres |
Como converter o valor de um campo do tipo CHAR ou VARCHAR em letras minúsculas usando a função LOWER() do FirebirdQuantidade de visualizações: 8578 vezes |
|
A função LOWER() do Firebird é usada quando precisamos converter o valor de um campo do tipo CHAR ou VARCHAR em letras minúsculas. A partir do Firebird 2 esta função consegue transformar em minúsculas até mesmo os caracteres não pertencentes ao conjunto ASCII (non-ASCII), mesmo se o collation padrão (binary) estiver sendo usado. Veja um exemplo de como usar esta função em uma query SQL DML SELECT FROM: SELECT NOME NORMAL, LOWER(NOME) MINUSCULAS FROM CLIENTES WHERE ID = 1; Ao executarmos esta query teremos o seguinte resultado: NORMAL MINUSCULAS OSMAR J. SILVA osmar j. silva A função LOWER() pode ser usada em DSQL (Dynamic SQL), ESQL (Embedded SQL) e PSQL (Stored procedure and trigger language). |
Ruby ::: Dicas & Truques ::: Programação Orientada a Objetos |
Programação Orientada a Objetos em Ruby: Classes, objetos, métodos e variáveis de instânciaQuantidade de visualizações: 11111 vezes |
|
A melhor forma de entender a programação orientada a objetos é começar com uma analogia simples. Suponha que você queira dirigir um carro e fazê-lo ir mais rápido pressionado o acelerador. O que deve acontecer antes que você seja capaz de fazer isso? Bem, antes que você possa dirigir um carro, alguém tem que projetá-lo. Um carro geralmente começa com desenhos feitos pelos engenheiros responsáveis por tal tarefa, tal qual a planta de uma casa. Tais desenhos incluem o projeto de um acelerador que possibilita ao carro ir mais rápido. O pedal do acelerador "oculta" os mecanismos complexos responsáveis por fazer o carro ir mais rápido, da mesma forma que o pedal de freio "oculta" os mecanismos que fazem o carro ir mais devagar e o volante "oculta" os mecanismos que fazem com que o carro possa virar para a direita ou esquerda. Isso permite que pessoas com pequeno ou nenhum conhecimento de motores possam facilmente dirigir um carro. Infelizmente, não é possível dirigir o projeto de um carro. Antes que possamos dirigí-lo, o carro deve ser construído a partir do projeto que o descreve. Um carro já finalizado tem um pedal de aceleração de verdade, que faz com que o carro vá mais rápido. Ainda assim, é preciso que o motorista pressione o pedal. O carro não acelerará por conta própria. Agora vamos usar nosso exemplo do carro para introduzir alguns conceitos de programação importantes à programação orientada a objetos. A execução de uma determinada tarefa em um programa exige um método ou função. O método (ou função) descreve os mecanismos que, na verdade, executam a tarefa. O método oculta tais mecanismos do usuário, da mesma forma que o pedal de aceleração de um carro oculta do motorista os mecanismos complexos que fazem com que um carro vá mais rápido. Em Ruby, começamos criando uma unidade de programa chamada classe para abrigar um método, da mesma forma que o projeto de um carro abriga o design do pedal de acelerador. Em uma classe fornecemos um ou mais métodos que são projetados para executar as tarefas da classe. Por exemplo, a classe que representa uma conta bancária poderia conter muitos métodos, incluindo um método para depositar dinheiro na conta, outro para retirar dinheiro, um terceiro para verificar o saldo, e assim por diante. Da mesma forma que não podemos dirigir o projeto de um carro, nós não podemos "dirigir" uma classe. Da mesma forma que alguém teve que construir um carro a partir de seu projeto antes que pudessémos dirigí-lo, devemos construir um objeto de uma classe antes de conseguirmos executar as tarefas descritas nela. Quando dirigimos um carro, o pressionamento do acelerador envia uma mensagem ao carro informando-o da tarefa a ser executada (neste caso informando-o de que queremos ir mais rápido). Da mesma forma, enviamos mensagens aos objetos de uma classe. Cada mensagem é uma chamada de método e informa ao objeto qual ou quais tarefas devem ser executadas. Até aqui nós usamos a analogia do carro para introduzir classes, objetos e métodos. Já é hora de saber que um carro possui atributos (propriedades) tais como cor, o número de portas, a quantidade de gasolina em seu tanque, a velocidade atual, etc. Tais atributos são representados como parte do projeto do carro. Quando o estamos dirigindo, estes atributos estão sempre associados ao carro que estamos usando, e cada carro construído a partir do projeto sofrerá variações nos valores destes atributos em um determinado momento. Da mesma forma, um objeto tem atributos associados a ele quando o usamos em um programa. Estes atributos são definidos na classe a partir da qual o objeto é instanciado (criado) e são chamados de variáveis de instância da classe. Veremos agora como definir uma classe em Ruby e usar um objeto desta classe em um programa. Veja o trecho de código abaixo:
# Definição da classe Cliente
class Cliente
def definir_nome(nome)
@nome = nome
end
def obter_nome
@nome
end
end
# Cria uma instância da classe Cliente
cliente = Cliente.new
# Efetua uma chamada ao método definir_nome
cliente.definir_nome("Laura Maria dos Santos")
# Efetua uma chamada ao método obter_nome
print "O nome do cliente é " + cliente.obter_nome
Ao executar este código Ruby nós teremos o seguinte resultado: O nome do cliente é Laura Maria dos Santos |
C ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o seno de um número ou ângulo em C usando a função sin()Quantidade de visualizações: 4725 vezes |
|
Em geral, quando falamos de seno, estamos falando do triângulo retângulo de Pitágoras (Teorema de Pitágoras). A verdade é que podemos usar a função seno disponível nas linguagens de programação para calcular o seno de qualquer número, mesmo nossas aplicações não tendo nenhuma relação com trigonometria. No entanto, é sempre importante entender o que é a função seno. Veja a seguinte imagem:  Veja que temos um triângulo retângulo com as medidas já calculadas para a hipotenusa e os dois catetos, assim como os ângulos entre eles. Assim, o seno é a razão entre o cateto oposto (oposto ao ângulo theta) e a hipotenusa, ou seja, o cateto oposto dividido pela hipotenusa. Veja a fórmula: \[\text{Seno} = \frac{\text{Cateto oposto}}{\text{Hipotenusa}} \] Então, se dividirmos 20 por 36.056 (na figura eu arredondei) nós teremos 0.5547, que é a razão entre o cateto oposto e a hipotenusa (em radianos). Agora, experimente calcular o arco-cosseno de 0.5547. O resultado será 0.9828 (em radianos). Convertendo 0.9828 radianos para graus, nós obtemos 56.31º, que é exatamente o ângulo em graus entre o cateto oposto e a hipotenusa na figura acima. Pronto! Agora que já sabemos o que é seno na trigonometria, vamos entender mais sobre a função sin() da linguagem C. Esta função, disponível no header math.h, recebe um valor numérico e retorna um valor, também numérico) entre -1 até 1 (ambos inclusos). Veja:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(int argc, char *argv[]){
printf("Seno de 0 = %f", sin(0));
printf("\nSeno de 1 = %f", sin(1));
printf("\nSeno de 2 = %f", sin(2));
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: Seno de 0 = 0.000000 Seno de 1 = 0.841471 Seno de 2 = 0.909297 Note que calculamos os senos dos valores 0, 1 e 2. Observe como os resultados conferem com a curva da função seno mostrada abaixo: 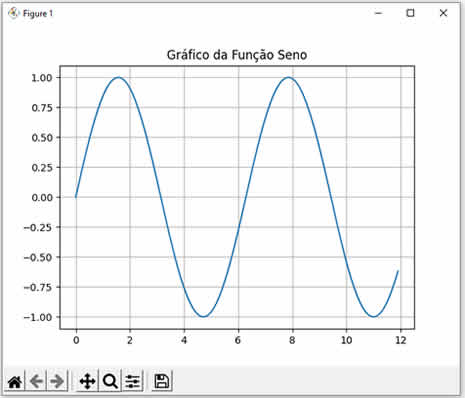 |
PHP ::: Dicas & Truques ::: Strings e Caracteres |
Manipulação de texto em PHP - Como acessar e modificar os caracteres individuais de uma stringQuantidade de visualizações: 231 vezes |
|
Os caracteres de uma string em PHP, ou seja, uma palavra, frase ou texto, podem ser acessados individualmente usando índices, igual fazemos com os vetores (o índice começando sempre em zero). Dessa forma, podemos tanto obter um determinado caractere quanto acessá-lo e modificá-lo. Veja um código PHP completo demonstrando o exemplo: <html> <head> <title>Estudando PHP</title> </head> <body> <?php $nome = "Carlos de Jesus"; echo "Original: " . $nome . "<br>"; echo "Vou alterar o 11º caractere.<br>"; $nome[10] = "M"; echo "Modificado: " . $nome; ?> </body> </html> Ao executar este código PHP nós teremos o seguinte resultado: Original: Carlos de Jesus Vou alterar o 11º caractere. Modificado: Carlos de Mesus |
Java ::: Dicas & Truques ::: Programação Orientada a Objetos |
Como usar encapsulamento em Java - Programação Orientada a Objetos em JavaQuantidade de visualizações: 37986 vezes |
|
Encapsulamento é a técnica de transformar os objetos que compõem uma aplicação em verdadeiras caixas-pretas. De fato, se pensarmos em termos de informática, é possível para um usuário comum usar todas as funcionalidades de uma impressora sem nem mesmo entender seu funcionamento interno. Imagine o desastre que seria se todos os usuários resolvessem abrir suas impressoras para investigar o que há dentro delas. Da mesma forma, ao construir uma classe, devemos fazê-lo de forma que o usuário desta classe tenha acesso apenas aos métodos que permitem ler informações da classe ou fornecer os dados necessários para sua correta operação. Dados relativos ao funcionamento interno da classe devem permanecer ocultos e acessíveis somente aos métodos da própria classe. O encapsulamento deve ser aplicado de forma a permitir que alterações na estrutura interna de uma classe não prejudique o funcionamento do código externo que a usa. Veja um exemplo:
class Pedido{
public List obterProdutos(){
// monta uma lista de produtos
// pertecentes a este pedido
return lista;
}
}
A classe Pedido contém um método chamado obterProdutos() que retorna uma lista de produtos pertencentes a um determinado pedido. É aqui que o encapsulamento se torna importante. O código que usa esta classe desconhece completamente como esta lista de produtos é montada. Tudo que nos interessa é a lista de produtos que o método retorna. O programador da classe pode decidir a qualquer momento, talvez para melhorar o desempenho da classe, alterar a forma de montagem da lista. Uma vez que o nome e retorno do método (incluindo a estrutura da lista retornada) continuem sendo os mesmos, o código que usa a classe continuará funcionando como anteriormente. |
C# ::: Dicas & Truques ::: Strings e Caracteres |
Como retornar uma substring de uma string C# usando o método Substring() da classe String - C# para iniciantesQuantidade de visualizações: 32896 vezes |
|
Esta dica mostra como obter parte de uma palavra, frase ou texto, ou seja, extrair uma substring a partir de uma string. Isso pode ser feito por meio da função Substring() da classe String da linguagem C#. Veja que temos que fornecer o índice do primeiro caractere (começando em 0) e a quantidade de caracteres que serão obtidos. Veja o código completo para o exemplo:
using System;
namespace Estudos{
class Program{
static void Main(string[] args) {
string frase = "Gosto muito de C#";
Console.WriteLine("A frase é: " + frase);
// obtém a substring "muito"
string substring = frase.Substring(6, 5);
Console.WriteLine("Substring obtida: " + substring);
Console.WriteLine("\n\nPressione uma tecla para sair...");
Console.ReadKey();
}
}
}
Ao executar este código nós teremos o seguinte resultado: A frase é: Gosto muito de C# Substring obtida: muito |
Java ::: Java para Engenharia ::: Geometria Analítica e Álgebra Linear |
Como calcular vetor unitário em Java - Java para Física e EngenhariaQuantidade de visualizações: 543 vezes |
|
Um vetor unitário ou versor num espaço vetorial normado é um vetor (mais comumente um vetor espacial) cujo comprimento ou magnitude é 1. Em geral um vetor unitário é representado por um "circunflexo", assim: __$\hat{i}__$. O vetor normalizado __$\hat{u}__$ de um vetor não zero __$\vec{u}__$ é o vetor unitário codirecional com __$\vec{u}__$. O termo vetor normalizado é algumas vezes utilizado simplesmente como sinônimo para vetor unitário. Dessa forma, o vetor unitário de um vetor __$\vec{u}__$ possui a mesma direção e sentido, mas magnitude 1. Por magnitude entendemos o módulo, a norma ou comprimento do vetor. Então, vejamos a fórmula para a obtenção do vetor unitário: \[\hat{u} = \dfrac{\vec{v}}{\left|\vec{v}\right|}\] Note que nós temos que dividir as componentes do vetor pelo seu módulo de forma a obter o seu vetor unitário. Por essa razão o vetor nulo não possui vetor unitário, pois o seu módulo é zero, e, como sabemos, uma divisão por zero não é possível. Veja agora o código Java que pede as coordenadas x e y de um vetor 2D ou R2 e retorna o seu vetor unitário:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
Scanner entrada = new Scanner(System.in);
// vamos ler os valores x e y
System.out.print("Informe o valor de x: ");
double x = Double.parseDouble(entrada.nextLine());
System.out.print("Informe o valor de y: ");
double y = Double.parseDouble(entrada.nextLine());
// o primeiro passo é calcular a norma do vetor
double norma = Math.sqrt(Math.pow(x, 2) + Math.pow(y, 2));
// agora obtemos as componentes x e y do vetor unitário
double u_x = x / norma;
double u_y = y / norma;
// mostra o resultado
System.out.println("O vetor unitário é: (x = " +
u_x + "; y = " + u_y);
}
}
Ao executar este código Java nós teremos o seguinte resultado: Informe o valor de x: -4 Informe o valor de y: 6 O vetor unitário é: (x = -0.5547001962252291; y = 0.8320502943378437 Veja agora uma modificação deste código para retornarmos o vetor unitário de um vetor 3D ou R3, ou seja, um vetor no espaço:
package estudos;
import java.util.Scanner;
public class Estudos {
public static void main(String[] args) {
Scanner entrada = new Scanner(System.in);
// vamos ler os valores x, y e z
System.out.print("Informe o valor de x: ");
double x = Double.parseDouble(entrada.nextLine());
System.out.print("Informe o valor de y: ");
double y = Double.parseDouble(entrada.nextLine());
System.out.print("Informe o valor de z: ");
double z = Double.parseDouble(entrada.nextLine());
// o primeiro passo é calcular a norma do vetor
double norma = Math.sqrt(Math.pow(x, 2)
+ Math.pow(y, 2) + Math.pow(z, 2));
// agora obtemos as componentes x, y e z do vetor unitário
double u_x = x / norma;
double u_y = y / norma;
double u_z = z / norma;
// mostra o resultado
System.out.println("O vetor unitário é: (x = " +
u_x + "; y = " + u_y + "; z = " + u_z);
}
}
Ao executarmos este novo código nós teremos o seguinte resultado: Informe o valor de x: 3 Informe o valor de y: 7 Informe o valor de z: 5 O vetor unitário é: (x = 0.329292779969071; y = 0.7683498199278324; z = 0.5488212999484517 |
Delphi ::: Imagens, Gráficos e Cores ::: TBitmap (A classe TBitmap) |
Computação gráfica em Delphi - Como usar a classe TBitmap do DelphiQuantidade de visualizações: 16634 vezes |
|
A classe TBitmap encapsula um bitmap Windows (HBITMAP, um handle para um bitmap), incluindo sua paleta (HPALETTE, um handle para uma paleta de cores). Esta classe herda de TGraphic e é usada para criar, manipular (redimensionar, rolar, rotacionar, pintar, etc) e armazenar imagens na memória e como arquivos em disco. A classe TBitmap contém muitas propriedades e métodos úteis. Entre seus métodos podemos citar LoadFromFile(), usado para carregar uma imagem bitmap a partir do disco e guardá-la em memória como um objeto TBitmap. Veja o trecho de código abaixo:
procedure TForm2.Button1Click(Sender: TObject);
var
bmp: TBitmap;
begin
// vamos criar o bitmap
bmp := TBitmap.Create;
// vamos carregar a imagem e guardá-la no bitmap
bmp.LoadFromFile('foto.bmp');
// vamos desenhar o bitmap no formulário
// começando nas coordenadas x = 0; y = 0 a partir
// do canto superior esquerdo da área cliente do formulário
Form2.Canvas.Draw(0, 0, bmp);
// vamos liberar o bitmap
bmp.Free;
end;
Aqui nós carregamos o bitmap foto.bmp e o desenhamos na superfície do formulário usando o método Draw() do Canvas do formulário. É possível também redimensionar o bitmap ao desenhá-lo no formulário. Veja este novo trecho de código:
procedure TForm2.Button1Click(Sender: TObject);
var
bmp: TBitmap;
retang: TRect; // um objeto TRect
begin
// vamos criar o bitmap
bmp := TBitmap.Create;
// vamos carregar a imagem e guardá-la no bitmap
bmp.LoadFromFile('foto.bmp');
// vamos redimensionar o bitmap na memória de
// acordo com o retângulo abaixo
retang.Top := 0;
retang.Left := 0;
retang.Right := 200;
retang.Bottom := 150;
// vamos desenhar o bitmap usando o método
// StretchDraw da classe TCanvas
Form2.Canvas.StretchDraw(retang, bmp);
// vamos liberar o bitmap
bmp.Free;
end;
Aqui nós usamos um objeto do registro (record) TRect para criar um retângulo especificando o tamanho do bitmap e fornecemos tal retângulo, juntamente com o bitmap, para o método StretchDraw() da classe TCanvas. Este método redimensiona a imagem antes de desenhá-la na superfície do formulário. Para fins de compatibilidade, esta dica foi escrita usando Delphi 2009. |
C ::: Dicas & Truques ::: Trigonometria - Funções Trigonométricas |
Como calcular o cateto adjascente dadas as medidas da hipotenusa e do cateto oposto em CQuantidade de visualizações: 2407 vezes |
|
Nesta dica mostrarei como podemos tirar proveito do Teorema de Pitágoras para obter a medida do cateto adjascente quando temos as medidas da hipotenusa e do cateto oposto. Este teorema diz que "o quadrado da hipotenusa é igual à soma dos quadrados dos catetos", o que torna a nossa tarefa, na linguagem C, muito fácil. Comece observando a imagem a seguir:  Veja que, nessa imagem, eu já coloquei os comprimentos da hipotenusa, do cateto oposto e do cateto adjascente. Para facilitar a conferência dos cálculos, eu coloquei também os ângulos theta (que alguns livros chamam de alfa) e beta já devidamente calculados. A medida da hipotenusa é, sem arredondamentos, 36.056 metros. Então, sabendo que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos (Teorema de Pitógoras): \[c^2 = a^2 + b^2\] Tudo que temos que fazer é mudar a fórmula para: \[b^2 = c^2 - a^2\] Veja que agora o quadrado do cateto adjascente é igual ao quadrado da hipotenusa menos o quadrado do cateto oposto. Não se esqueça de que a hipotenusa é o maior lado do triângulo retângulo. Veja agora como esse cálculo é feito em linguagem C:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(int argc, char *argv[]){
float c = 36.056; // medida da hipotenusa
float a = 20; // medida do cateto oposto
// agora vamos calcular a medida da cateto adjascente
float b = sqrt(pow(c, 2) - pow(a, 2));
// e mostramos o resultado
printf("A medida do cateto adjascente é: %f", b);
printf("\n\n");
system("PAUSE");
return 0;
}
Ao executar este código C nós teremos o seguinte resultado: A medida do cateto adjascente é: 30.000586 Como podemos ver, o resultado retornado com o código C confere com os valores da imagem apresentada. |
Nossas 20 dicas & truques de programação mais populares |
|
Python - Como tratar o evento wx.EVT_PAINT em suas aplicações wxPython - Interfaces gráficas no Python |
Você também poderá gostar das dicas e truques de programação abaixo |
|
R - R para Matemática e Estatística - Como calcular desvio padrão usando a função sd() da linguagem R Python - Datas e horas em Python - Como obter a hora como um decimal no intervalo 00-12 (formato 12 horas) JavaScript - Como retornar uma coleção de nós filhos de um elemento HTML usando a propriedade childNodes do DOM do JavaScript QGIS - Como definir o título do projeto do QGIS usando PyQGIS e a função setTitle() da classe QgsProject |
Nossas 20 dicas & truques de programação mais recentes |
Últimos Projetos e Códigos Fonte Liberados Para Apoiadores do Site |
|
Python - Como criar o jogo Pedra, Papel, Tesoura em Python - Jogo completo em Python com código comentado |
Últimos Exercícios Resolvidos |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |





