Você está aqui: VB.NET ::: Desafios e Lista de Exercícios Resolvidos ::: Arrays e Matrix (Vetores e Matrizes) |
Como testar se uma matriz é uma Matriz Triangular Superior em VB.NET - Desafio de Programação Resolvido em VB.NETQuantidade de visualizações: 648 vezes |
|
Pergunta/Tarefa: Uma Matriz Triangular Superior é a matriz na qual todos os termos que estão abaixo da diagonal principal são iguais a zero e os termos que estão acima da diagonal principal são números reais. Veja um exemplo de Matriz Triangular Superior na imagem abaixo: 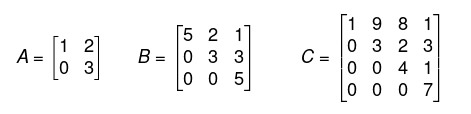 Escreva um programa VB.NET que pede para o usuário informar o número de linhas e colunas de uma matriz quadrada. Em seguida solicite os valores para cada um dos elementos da matriz. Para finalizar informe ao usuário se a matriz informada é uma matriz triangular superior. Sua saída deverá ser parecida com:
Número de linhas e colunas da matriz: 3
Valor para a linha 0 e coluna 0: 8
Valor para a linha 0 e coluna 1: 2
Valor para a linha 0 e coluna 2: 3
Valor para a linha 1 e coluna 0: 0
Valor para a linha 1 e coluna 1: 3
Valor para a linha 1 e coluna 2: 9
Valor para a linha 2 e coluna 0: 0
Valor para a linha 2 e coluna 1: 0
Valor para a linha 2 e coluna 2: 2
Valores na matriz
8 2 3
0 3 9
0 0 2
A matriz é uma matriz triangular superior
Veja a resolução comentada deste exercício usando VB.NET:
Imports System
Module Program
' função principal do programa VB.NET
Sub Main(args As String())
' vamos pedir a ordem da matriz
Console.Write("Número de linhas e colunas da matriz: ")
Dim ordem As Integer = Int32.Parse(Console.ReadLine())
' vamos declarar uma matriz 3x3
Dim matriz(ordem - 1, ordem - 1) As Integer
' vamos pedir para o usuário informar os valores
' dos elementos da matriz, uma linha de cada vez
Console.WriteLine()
For i As Integer = 0 To matriz.GetUpperBound(0)
For j As Integer = 0 To matriz.GetUpperBound(1)
Console.Write("Linha " & (i + 1) & " e coluna " &
(j + 1) & ": ")
' lê o número e guarda na linha e coluna especificadas
matriz(i, j) = Integer.Parse(Console.ReadLine())
Next
Next
' vamos mostrar a matriz da forma que ela foi informada
Console.WriteLine(vbCrLf & "Valores na matriz: " & vbCrLf)
For i As Integer = 0 To matriz.GetUpperBound(0)
For j As Integer = 0 To matriz.GetUpperBound(1)
Console.Write(matriz(i, j).ToString().PadLeft(5) & " ")
Next
' passa para a próxima linha
Console.WriteLine()
Next
' agora vamos testar se a matriz é uma matriz triangular
' superior
Dim triangular_superior As Boolean = True
For i As Integer = 0 To matriz.GetUpperBound(0)
For j As Integer = 0 To matriz.GetUpperBound(1)
' a condição para que a matriz seja triangular superior é
' que os elementos abaixo da diagonal principal sejam
' iguais a zero
If ((j < i) And (matriz(i, j) <> 0)) Then
triangular_superior = False
End If
Next
Next
If (triangular_superior) Then
Console.WriteLine(vbCrLf & "A matriz é uma matriz triangular superior")
Else
Console.WriteLine(vbCrLf & "A matriz não é uma matriz triangular superior")
End If
Console.WriteLine(vbCrLf & "Pressione qualquer tecla para sair...")
' pausa o programa
Console.ReadKey()
End Sub
End Module
Listamos abaixo algumas propriedades específicas da matriz triangular. 1) o determinante de uma matriz triangular é igual ao produto dos termos da diagonal principal. 2) o produto entre duas matrizes triangulares é uma matriz triangular. 3) se um dos termos da diagonal principal da matriz triangular for igual a zero, então o seu determinante será igual a zero e, consequentemente, ela não será inversível. 4) a matriz inversa de uma matriz triangular é também uma matriz triangular. 5) a soma de duas matrizes triangulares superiores é uma matriz triangular superior; de forma análoga, a soma de duas matrizes triangulares inferiores é uma matriz triangular inferior. |
|
|
Mais Desafios de Programação e Exercícios e Algoritmos Resolvidos de VB.NET |
Veja mais Dicas e truques de VB.NET |
Dicas e truques de outras linguagens |
E-Books em PDF |
||||
|
||||
|
||||
Linguagens Mais Populares |
||||
|
1º lugar: Java |







